一種求解大規模方程組的修正Dai-Yuan共軛梯度法

黎 勇， 鄧娌莉

(百色學院 數學與統計學院， 廣西 百色 533000)

一種求解大規模方程組的修正Dai-Yuan共軛梯度法

黎 勇*， 鄧娌莉

(百色學院 數學與統計學院， 廣西 百色 533000)

設計一種針對大規模非線性方程組的修正DY共軛梯度算法.該算法的搜索方向不僅自動滿足充分下降條件，而且屬于信賴域.在適當條件下，可以證明新算法是全局收斂的.初步的數值實驗表明新算法可以有效求解大規模非線性方程組．

非線性方程組； 共軛梯度法； 大規模； 信賴域； 全局收斂

考慮非線性方程組：

f(x)=0，x∈Rn，

(1)

其中f:Rn→Rn連續可微.求解此類問題的方法很多，將方程組問題轉化為最優化問題是其中的一種思想.令

minφ(x)，x∈Rn，

(2)

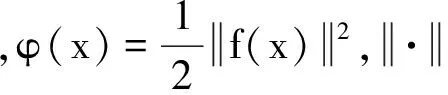
共軛梯度法的一般迭代格式如下：

xk+1=xk+αkdk，

(3)

(4)

其中,αk是步長，dk是搜索方向，不同的βk對應著不同的共軛梯度法，最經典的有HS方法、FR方法、PRP方法、DY方法等[1]．

不少研究人員在應用共軛梯度思想求解非線性方程組方面進行了討論，也取得了較好的研究結果.本文受文獻[2]和[3]的思想方法的啟發，將在經典DY共軛梯度法的基礎上，利用投影技術，提出一種修正的DY投影共軛梯度法．

1 算法

新算法的搜索方向設計如下：

dk+1=

(5)

其中,f(xk+1)=fk+1，f(xk)=fk，yk=fk+1-fk，而λ1>0，λ2>0是常數.在此基礎上，下面將給出新算法.新算法采用以下線搜索[4]：

-f(xk+αkdk)Tdk≥

(6)

這里αk=max{s，λs，λ2s，…}，σ>0，s>0，λ∈(0，1)．

算法1(MDY算法)：

步0. 選取初始點x0∈Rn.常數ε∈(0，1)，參數λ1>0，λ2>0，σ>0.令k:=0．

步2. 利用(5)式計算搜索方向dk+1．

步3. 由線搜索技術(6)式計算步長αk．

步4. 利用以下公式計算下一個迭代點zk=xk+αkdk．

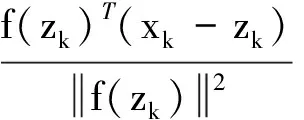
(7)

步6. 令k:=k+1.轉步1．

注：(7)式表示算法的下一個迭代點xk+1應當通過將當前迭代點xk投射到超平面Hk={x∈Rnf(zk)T(x-zk)=0}上獲得，這一思想由Solodov和Svaiter在文獻[5]提出．

2 全局收斂性分析

引理1設dk滿足(5)式，則有：

(8)

和

(9)

證明當k=0時，結論顯然成立．

當k≥1時，根據(5)式可得

即(8)式成立．

依據(8)式，利用Cauchy-schwartz不等式得

故

綜上所述，(9)式得證. 證畢.

上述引理說明新算法不僅自動具有獨立于線搜索的充分下降性質，而且搜索方向具有信賴域性質，這兩個重要性質對算法全局收斂性的證明非常重要.下面利用文獻[2]和[3]的思想方法討論新算法的全局收斂性.以下兩個假設是后文討論的依據：

假設(i)：非線性方程組(1)有解．

假設(ii)：f(x) Lipschitz 連續，即存在一個正的常數L，使得

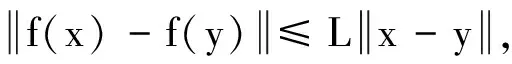
(10)

由假設(ii)容易推出存在一個正的常數γ，使得

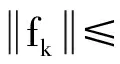
(11)

引理2若假設(i)、(ii)成立，則算法1是可行的．

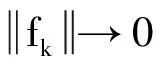
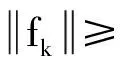
(12)

下面證明滿足線搜索(6)式的步長有下界．

反證法.假設存在k′使(6)式不成立，則對?m∈∪{0}，令有

由(8)式和假設(ii)有

(13)

而由(9)、(11)式可以推出

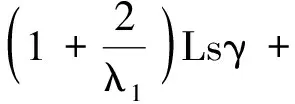
(14)

聯立(9)、(13)、(14)式可得

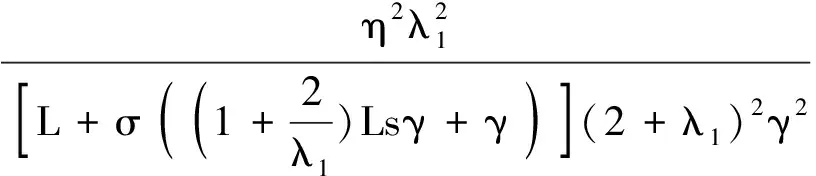
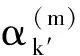
引理3設序列{xk}由算法1產生，假設(i)、(ii)成立，且f(x*)=0，則

和

成立．

引理3及其證明詳見文獻[5]．

定理1若假設(i)、(ii)成立，αk，dk，xk，fk都由算法1產生，則

(15)

證明假設(15)式不成立，則存在一個正的常數η，使

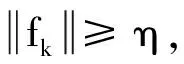
由(9)式有

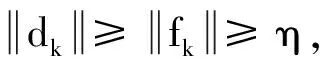
(16)

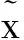
而由(9)、(11)式容易得到

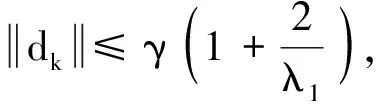
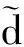
根據引理2、引理3以及(3)式容易知道

因此

(17)

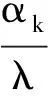
(18)

當k→∞時，對?k∈N2，上式兩邊同取極限得

而(8)式兩邊同取極限得

矛盾.所以(15)式成立.證畢.

3 數值試驗

本節將對MDY算法與傳統DY算法在求解大規模非線性方程組方面進行數值試驗和比較，測試的所有程序都是在Matlab R2010b上運行. 承擔測試任務的計算機配置如下：Win 7.Pentium Dual E5800 3.20 GHz，內存2.0 G. 本次試驗共選取文獻[4]中的9個非線性函數進行測試，測試函數見表1．

表1 測試問題

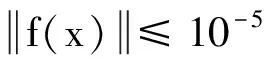
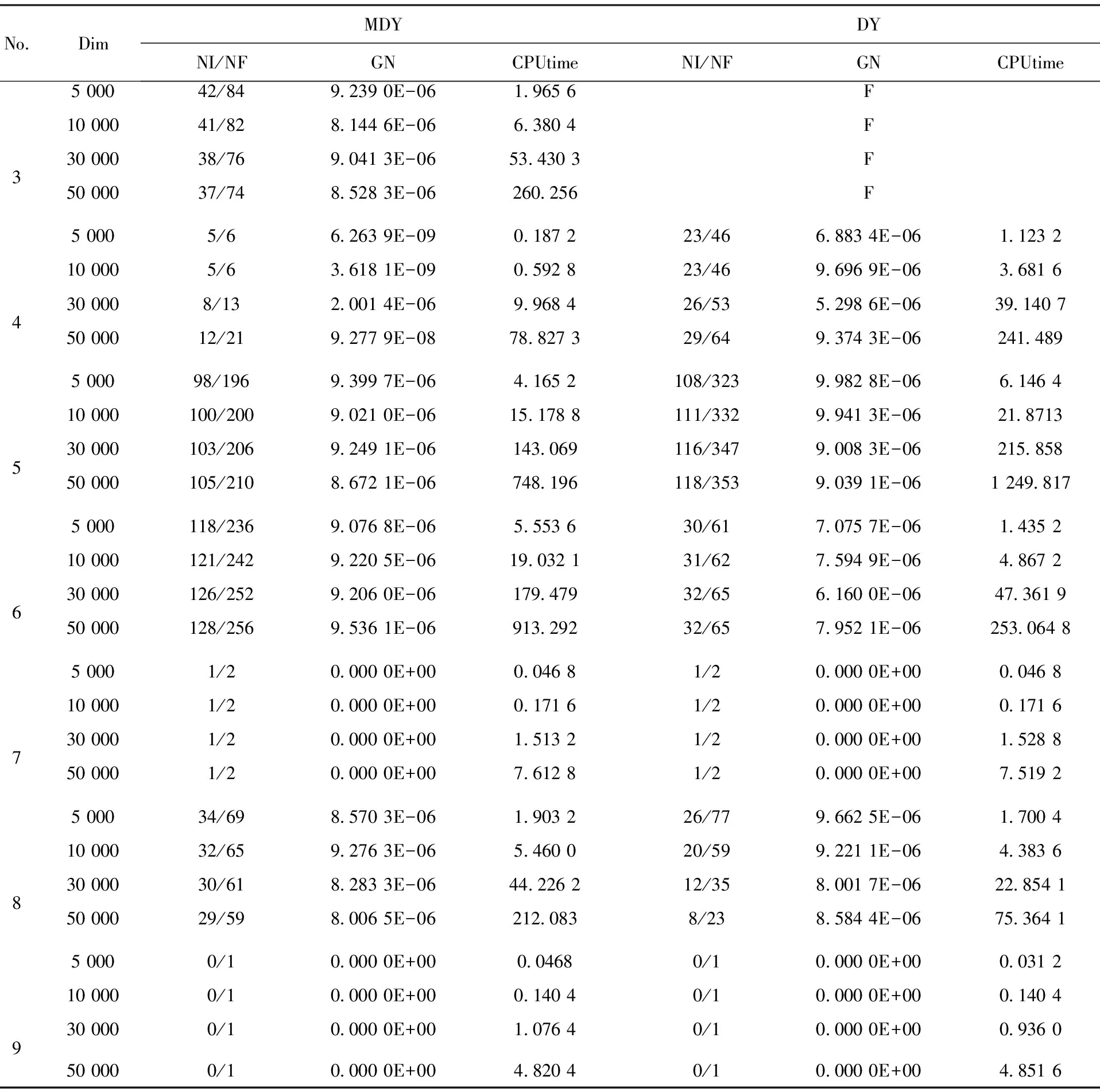
續表2

上表中No.表示測試問題的序號，Dim表示問題的維數，NI表示算法迭代次數，NF表示函數值的計算次數，GN表示程序終止時f(x)的范數值，CPUtime表示實驗所需時間(單位為秒)，F表示失敗.從表2中的數據容易看出，針對測試問題1，2，3，MDY算法能成功求解，而DY算法對這3個問題基本失敗(問題2中的5 000維和30 000維情形除外).對問題4和5來說，MDY算法無論是迭代次數、函數值計算次數，或者是運算消耗時間上均優于DY算法.對問題7和9的求解效果，兩種算法基本一致. 當然，在問題6和8的求解上，DY方法也一定程度上表現出了它的優勢. 綜上所述，我們認為新算法能夠有效求解大規模非線性方程組問題，而且新算法MDY總體上的數值表現要優于傳統的DY算法．

[1] 戴彧虹， 袁亞湘. 非線性共軛梯度法[M].上海:上海科技出版社，1999．

[2] YUAN G， ZHANG M. A three-terms Polak-Ribière-Polyak conjugate gradient algorithm for large-scale nonlinear equations[J]. Journal of Computational and Applied Mathematics， 2015，286: 186-195．

[3] YUAN G， ZHANG M， LI Y. A modified hestenes and stiefel conjugate gradient algorithm for large-scale nonsmooth minimizations and nonlinear equations[J]. Journal of Optimization Theory and Application， 2016，168: 129-152．

[4] LI Q， LI D. A class of derivative-free methods for large-scale nonlinear monotone equations[J]. IMA Journal of Numerical Analysis， 2011，31(4):1625-1635．

[5] SOLODOV M V， SVAITER B F. A Globally Convergent Inexact Newton Method for Systems of Monotone Equations[C]//FUKUSHIMA M， QI L. Reformulation: Nonsmooth， Piecewise Smooth， Semismooth and Smoothing Methods. US: Springer， 1998:355-369．

AmodifiedDai-Yuanconjugategradientalgorithmforlarge-scalenonlinearequations

LI Yong, DENG Lili

(School of Mathematics and Statistics， Baise University， Baise， Guangxi 533000, China)

This paper gives a modified Dai-Yuan conjugate gradient algorithm for large-scale nonlinear equations.The presented search direction not only possesses the sufficient descent property but also belongs to a trust region.The new algorithm has the global convergence under appropriate conditions.Numerical results show that this proposed algorithm is more effective than that of the normal method for large scale nonlinear equations．

nonlinear equation; conjugate gradient methods; large-scale; trust region; global convergence

2017-02-20.

國家自然科學基金項目(11661001，11661009)； 廣西省自然科學基金項目(2014GXNSFAA118030)；廣西省教育廳科研項目(YB2014389)．

*E-mail: liyong@3922@163.com．

10.19603/j.cnki.1000-1190.2017.06.002

1000-1190(2017)06-0731-05

O224

A