基于模糊C-Means的改進型KNN分類算法

朱付保， 謝利杰， 湯萌萌， 朱顥東

(鄭州輕工業學院 計算機與通信工程學院， 鄭州 450002)

基于模糊C-Means的改進型KNN分類算法

朱付保， 謝利杰， 湯萌萌， 朱顥東*

(鄭州輕工業學院 計算機與通信工程學院， 鄭州 450002)

KNN算法是一種思想簡單且容易實現的分類算法，但在訓練集較大以及特征屬性較多時候，其效率低、時間開銷大.針對這一問題，論文提出了基于模糊C-means的改進型KNN分類算法，該算法在傳統的KNN分類算法基礎上引入了模糊C-means理論，通過對樣本數據進行聚類處理，用形成的子簇代替該子簇所有的樣本集，以減少訓練集的數量，從而減少KNN分類過程的工作量、提高分類效率，使KNN算法更好地應用于數據挖掘.通過理論分析和實驗結果表明，論文所提算法在面對較大數據時能有效提高算法的效率和精確性，滿足處理數據的需求.

模糊C-Means； 聚類； KNN分類

隨著信息時代的發展，存儲能力的不斷提升，數據增長的速度也日益加快.然而存儲數據的結構也變得復雜多樣，如何在有效的時間內完成數據的處理成為當前關注的問題之一.為了在數據產生后的有效時間內挖掘出隱藏的信息，實現信息的價值，因此在數據的處理速度方面有更高的要求.

數據挖掘中K最近鄰(k-Nearest Neighbor，KNN)分類算法是一個理論上比較成熟的方法，也是數據分析和預測常用到的技術.在數據量較小的情況下，KNN分類算法能夠快速有效的實現數據的分類.由于KNN需要存放所有的訓練樣本，不需要事先建立模型，有新樣本需要分類時才創建，當數據量較大結構復雜時，算法的時間開銷大，且精確度有所下降，因此運用KNN分類算法進行數據挖掘面臨著困難.不少學者提出了改進的方法，閆永剛等提出了用MapReduce并行編程模型，同時結合KNN 算法自身的特點，給出了KNN 算法在Hadoop平臺下的并行化實現，提高KNN算法處理大數據集的能力[1].劉應東、牛惠民等提出了提出一種基于聚類技術的小樣本集KNN分類算法，算法通過進行聚類形成與各類樣本密度相近的新樣本集，在根據新樣本集的特征對輸入的未知樣本對象進行分類標識[2].陳海彬、郭金玉等提出了，提出一種基于改進K-means 聚類的KNN 故障檢測方法，其首先通過改進K-means 聚類將原始建模數據分成C個類，然后利用KNN 分別對每個類建立模型[3].羅賢鋒、祝勝林等提出基于K-Medoids聚類的改進KNN算法為提高海量數據的分類效率，其利用K-Medoids算法對文本訓練集進行聚類，分成相似度較高的簇，根據待分類文本與簇的相對位置，對文本訓練集進行裁剪[4].這些方法對于KNN分類算法的執行效率及準確度都有很大提高.但是學者們對于模糊C-means降低KNN分類算法的復雜度研究的相對較少.KNN分類算法處理大樣本數據效率會大大降低；當最近鄰近分類器K很小時，其對數據噪音很敏感，分類的準確度降低，因此提出了基于模糊C-means的改進型KNN分類算法，通過C-means聚類算法對樣本數據進行聚類處理，以減少數據分類的工作量，同時減弱無關屬性對分類結果的干擾.

1 相關基礎知識

1.1 KNN分類算法

K最近鄰(k-Nearest Neighbor，KNN)分類算法，是一個理論上比較成熟的數據分類方法.

該方法的思路是：存在一個樣本數據集合，也稱為訓練樣本集，并且樣本集中每個數據都存在標簽，即事先知道樣本集中每一數據與所屬分類的對應關系.輸入新的待分類的新樣本數據時，新的樣本數據的每個特征屬性將和訓練樣本集數據集中的對應特征值進行比較，然后分類算法來提取樣本集中特征最相似數據(最鄰近)的分類標簽.在進行分類時，大多情況只選擇樣本數據集的前K個相似度最高的數據，然后選擇K個最相似數據集中出現次數最多的分類作為新的數據集分類.

KNN分類算法最初由Cover和Hart提出用于解決文本分類的問題[5].算法是為了將輸入的測試數據點X分類為與該點最接近的K個鄰近特征分類中出現最多的那個類別[6].K近鄰算法是一種從測試數據點X開始，經過不斷的擴展范圍區域，一直把K個訓練樣本點都包含進去才停止，在歸類的過程中，該算法會把測試樣本點X歸為距離最近的K個訓練樣本點中出現頻率最大的類別.其中測試樣本與訓練樣本的相似度一般使用歐式距離測量.

如果將K的取值固定下來，并且訓練樣本個數能夠趨于無窮大，那么得到所有的K個鄰近都將收斂于X.如同最近鄰規則一樣，K個近鄰的標記都是隨機變量，概率pwi|x，i=1，2，…，K都是相互獨立的.假設pwm|x是較大的那個后驗概率，那么根據貝葉斯分類規則，則選取類別wm.而最近鄰規則是以概率pwm|x來選取類別，根據K近鄰規則，只有當K個最近鄰中的大多數的標記記為wm，才判定為類別wm[7-8].做出這樣斷定的概率為:

(1)

通常K值越大，選擇類別wm概率也越大.

1.2 模糊C-means聚類算法

傳統聚類分析算法把待識別的樣本對象嚴格的劃分到對應的類中，只有“是或否”兩種歸類，按這種算法劃分的界限是分明的.但是對于現實應用中，其樣本屬性并沒有嚴格的屬性，它們在形態和屬性等方面存在中介性，可能同時滿足兩種對立的特性，因此傳統的聚類分析算法無法解決這類問題.

為了更好的解決聚類問題，Dunn利用Ruspini提出的模糊劃分的概念，將其推廣應用到了模糊聚類上，后來Bezdek又將Dunn的工作推廣到基于模糊度m的一般C-means形式，提出了模糊C均值聚類(FCM)，這是一種根據傳統的聚類的改進算法，其目標函數定義如同C-means聚類算法，該算法基于數據樣本集的隸屬度，不同于傳統的聚類嚴格的把樣本單純的歸于某一類中.但是其權重矩陣W不在是二元矩陣，而是應用了模糊理論的概念，以其歸屬程度表示屬于各聚類的程度.

模糊C-means聚類把n個樣本集合Xi(i=1，2，3，…，n)分成對應的k個模糊組，計算出各組對應的聚類中心，使按價值函數求出的非相似性系數最小.模糊C-means聚類算法引用了模糊劃分的概念，為了確定其屬于各個組的程度，要求算法給每個樣本數據點用0到1之間的值來表示隸屬度[9-10].但是一個數據樣本集的隸屬度總和相加等于1.

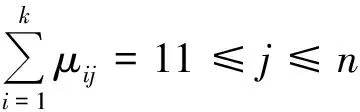
(2)

其中，模糊C-means聚類的樣本集合Xi(i=1，2，3，…，n)目標函數公式為：

(3)

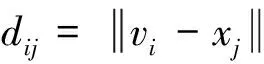
模糊C-means聚類算法的具體實現步驟如下：

1)首先用[0，1]間的隨機數來初始化樣本集的隸屬度，生成隸屬矩陣M，使其滿足隸屬度總和相加等于1的條件.

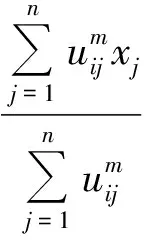
3)根據價值函數公式計算出其對應的價值函數.如果計算出的價值函數小于規定的閾值或者相對上次價值函數值的改變量小于某個閥值，則算法停止[11-13].

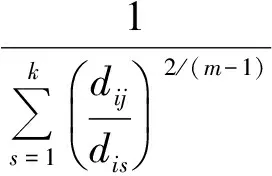
2 本文所提算法

2.1 算法基本思想

首先把樣本集合經過處理分成對應的K個模糊分組，其分組的理論是根據樣本集的隸屬度為依據，將其中的模糊子集A中的所有樣本X，為其定義一個數值μA(x)∈[0，1]來作為樣本X對A集合的隸屬度，從而來確定聚類分組的數目，再根據劃分的組進一步確定每個分組對應的聚類中心vi(i=1，…，k)，進而初始化加權指數m.其次根據聚類處理后形成的子簇數據分類，在子簇數據中按照KNN算法，在子簇集合中找出與測試樣本相對接近的所有樣本集合，然后根據得到的最鄰近列表樣本的多數類進行分類.

算法的實現基本流程圖如圖1所示.

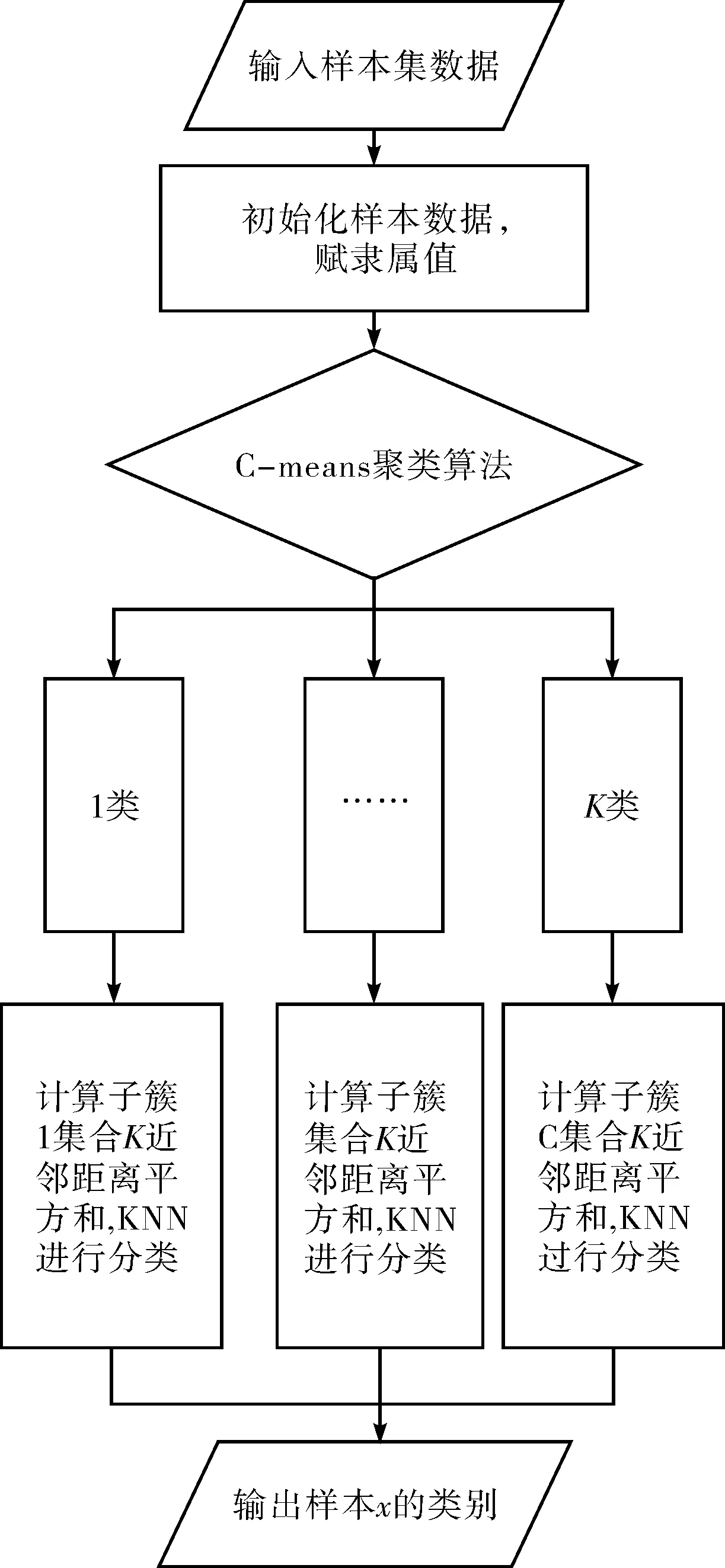
圖1 本文算法流程圖Fig.1 Flow chart of the proposed algorithm

2.2 算法具體描述

根據模糊分組理論，本文算法具體描述如下：

輸入：樣本集D=x1，x2，…，xn，其x1，x2，…，xn為樣本集D的屬性集，C=c1，c2，…，cm是簇數為K的類別屬性.

輸出：樣本屬性值x的所屬類別號.

1) 待分類的樣本集x1，x2，…，xn進行初始化，其中?xi∈R1≤i≤n，設置分類的種類數值為k，即劃分成k個模糊分組.設置樣本集xi的隸屬度，滿足所有樣本的隸屬度(權重)的和為1，生成隸屬矩陣M.

2) 根據模糊聚類中心求解公式，求出各個分組的中心點vi(i=1，…，k).

3) 根據價值函數公式計算出其對應的價值函數，判斷是否收斂，如果不滿足收斂條件則重新構造出新的矩陣M，再返回2).

4) 根據劃分的分組形成的子簇來代替該子簇的樣本集合，對子簇中的樣本用x，y的形式表示，則具有n個屬性的樣本為x1，x2…xn，y，y是樣本的類標號.

5) 依次計算出每個測試樣本t=x'，y'與每個訓練樣本x，y之間的距離d.

6) 按照距離的遞增依次排序.

7) 取出與測試樣本點距離最小的k個點.

8) 根據取出的點，確定這K個點所在類別出現的頻率.

9) 根據計算的頻率值，返回K個點中頻率最高的類別作為當前點的預測分類.

3 實驗對比與分析

為了驗證文中改進算法的有效性，以某房地產公司2012年至2016年房屋銷售管理的數據為例進行實驗對比，其中數據包含客戶信息、房屋信息、銷售人員信息等.實驗的硬件環境為Intel i7處理器，主頻為3.6 GHz，內存為 4 GB；實驗的軟件環境為Microsoft Windows 7 操作系統，Microsoft SQL Server 2005數據庫，Eclipse Luna 4.4.2，jdk7.0；算法實現的語言為java.

本文實驗主要選取房地產公司2012年～2016年銷售信息作為實驗的數據集合.各數據集的詳細信息如表1和表2所示.

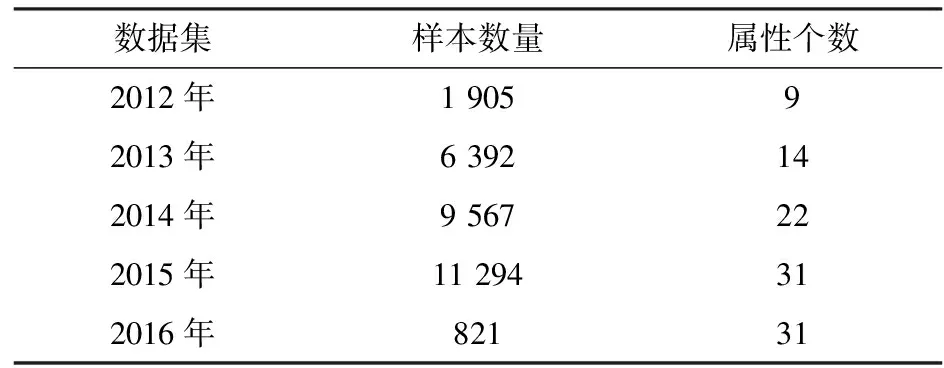
表1 實驗數據集

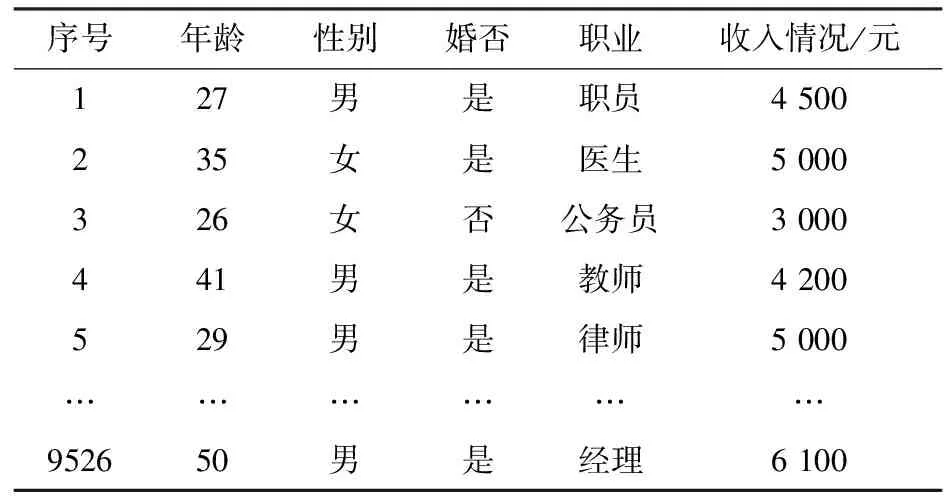
表2 部分客戶信息

為驗證改進算法的有效性，實驗設計了兩組實驗進行對比.本實驗選取基于K-means的KNN分類算法、基于K-Medoids的KNN算法和本文改進算法(基于模糊C-means的KNN分類算法)作比較.本文為改進算法了實現數據的分類，根據需要分類數據的業務背景，簡化實驗復雜度，設定了實驗K值為定值2(是否購買)，用以分類來預測訪客戶購房行為.算法的性能評估從算法的執行效率和分類結果的準確度兩個方面來衡量，執行效率方面比較兩種算法在同一實驗環境下處理同一組數據集的時間.

第一組實驗選取了數據集最大的2015年作為數據模型.對2015年的數據集實驗測試結果對比如圖2和圖3所示.

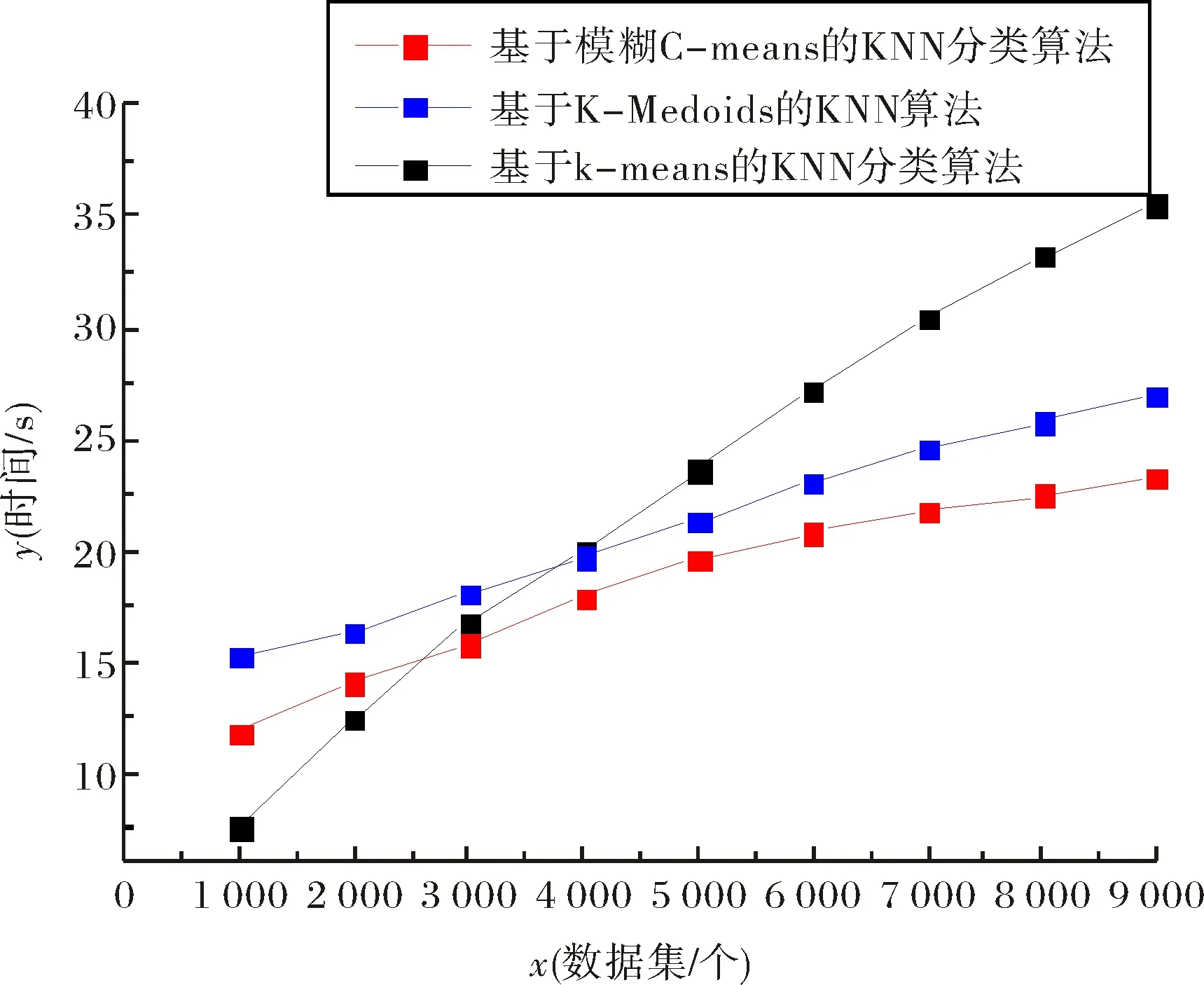
圖2 各算法在2015年數據集上的運行時間比較結果Fig.2 Comparative results of the running time of algorithms on the 2015 data set

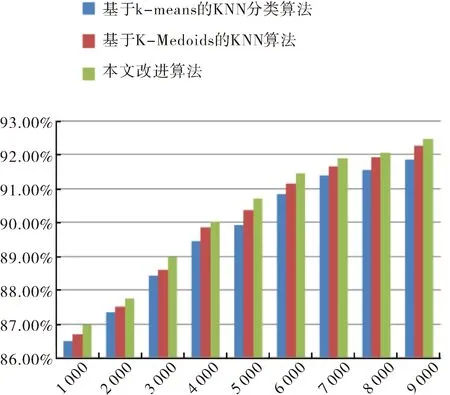
圖3 各算法在2015年的數據集上的分類準確度比較結果Fig.3 Comparative results of the classification accuracy of algorithms on the 2015 data set

第二組實驗使用了2012年～2016年的全部數據集.在各個數據集上進行分類算法的對比實驗測試結果如表3.

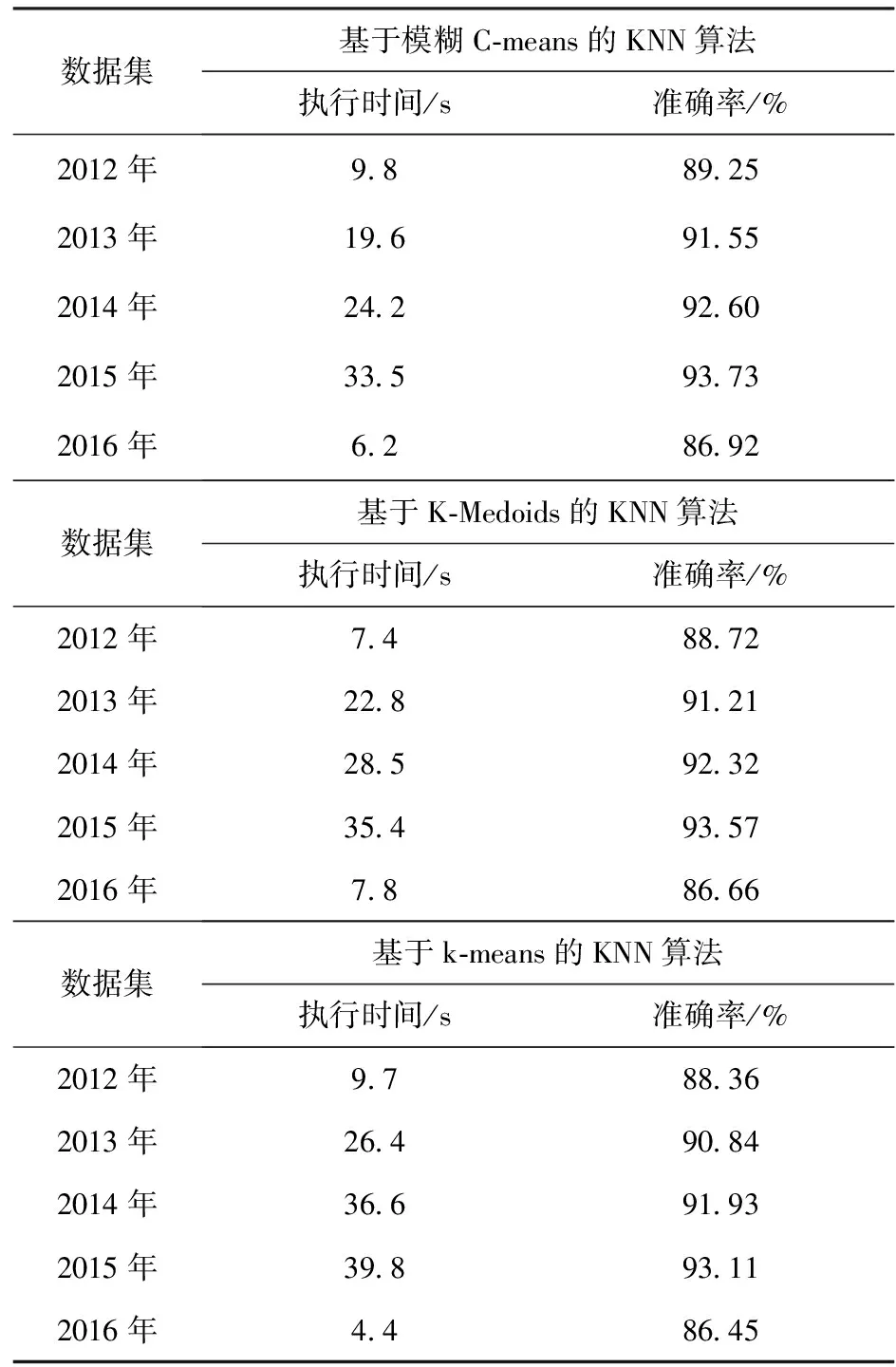
表3 實驗測試結果

根據上述對5組數據分別用兩種算法測試，其對比結果如圖4和圖5所示.

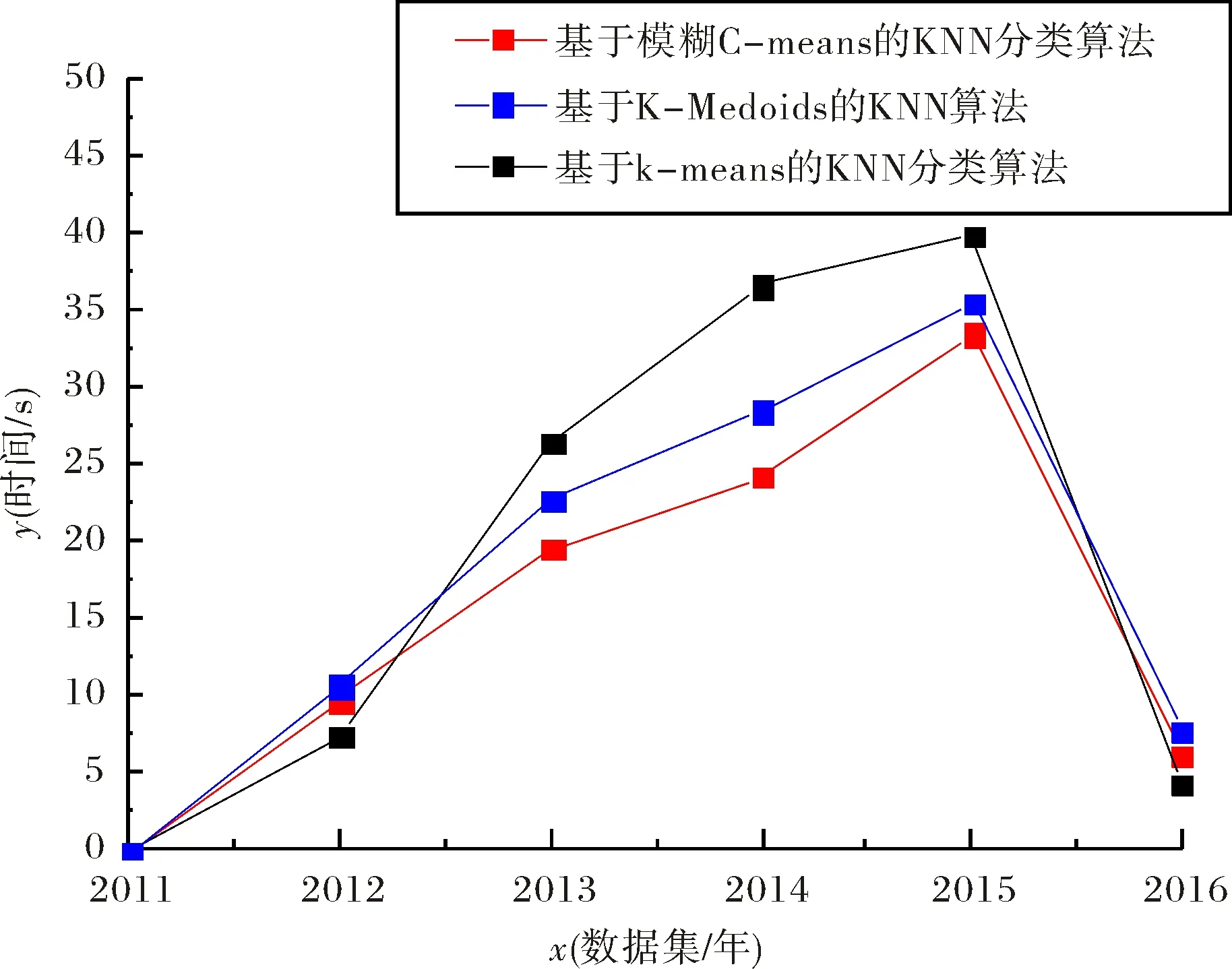
圖4 各算法在各數據集上的運行時間比較結果Fig.4 Comparative results of the running time of algorithms on the data sets

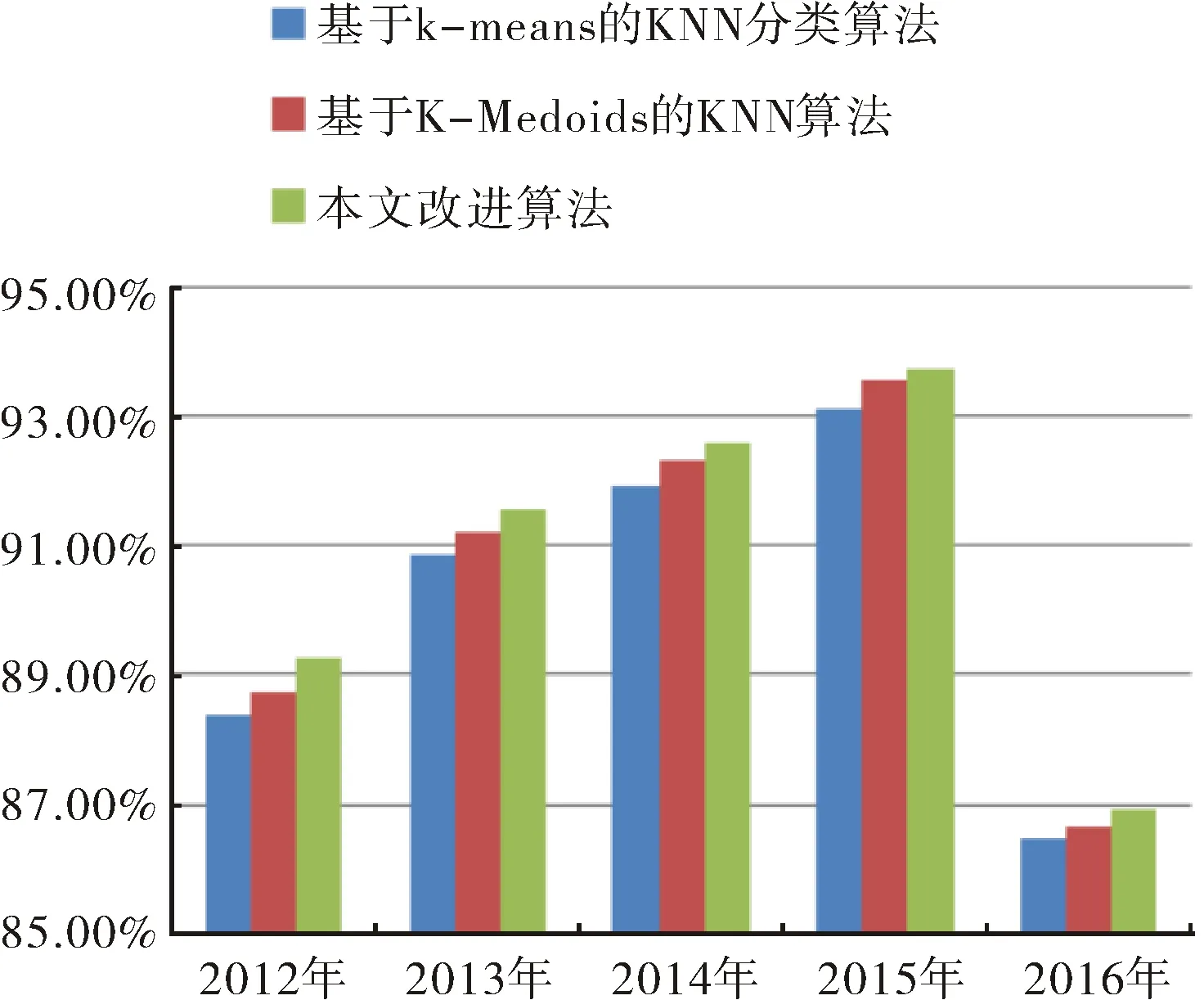
圖5 各算法在各數據集上的分類準確度比較結果Fig.5 Comparative results of the classification accuracy of algorithms on the data sets

本文改進算法與基于K-means的KNN分類算法、基于K-Medoids的KNN算法相比，其主要區別在于本文算法融入了模糊分組理論，使得每一個輸入的樣本數據不再僅隸屬于特定的聚類，而是以其隸屬程度來表示，對樣本集進行聚類，減少分類過程中的算法的計算量，提高了算法執行的效率，充分的發揮了該算法處理大樣本集、高維度數據的優勢.

從圖2～圖5中的實驗對比結果來看，對于第一組實驗采用2015年數據集，隨著實驗樣本量的增大，本文提出的改進算法比基于K-means的KNN分類算法、基于K-Medoids的KNN算法執行效率和分類的準確率高.對第二組實驗用了2012年至2016年的五個數據集，本文提出的改進算法在執行效率方面大都略優于其他兩種分類算法，同樣在分類的準確率方面也高.但對于小樣本集，如第一組實驗中的小樣本集和第二組實驗中的2016年數據集，本算法所執行的效率略低于基于K-means的KNN分類算法，主要是由于本文算法在執行的過程中進行模糊分組聚類需要耗費一部分時間，在樣本量小的情況下，雖然能夠減少分類樣本的數據量，但是這種時間的減少在整體效果上體現不明顯，另一方面改進算法準確率高于基于K-means的KNN分類算法.對于2015年的較大數據集處理上，本算法不僅能在準確率上有所提高，而且在執行分類能力方面高于基于K-means的KNN分類算法.結果表明，相同條件下，基于模糊C-means的KNN分類算法比基于K-means的KNN分類算法運行時間短，在執行大樣本集分類時效率方面優于基于K-means的KNN分類算法，且算法分類準確率更高；本文改進后的算法與基于K-Medoids的KNN算法相比較執行效率略高，由于基于K-Medoids的KNN算法需要得逐步計算直到類收斂，消耗一部分時間.通過兩組實驗對比，本文提出的改進算法對比之前兩種算法在分類性能均有所提高.

4 結束語

本文針對KNN分類算法在處理數據量大、維度高的樣本效率低的問題，提出了一種基于模糊C-means的KNN分類算法，利用樣本集隸屬程度的特性，對樣本集進行聚類，然后根據聚類形成的子簇來代替該子簇的所有樣本集，從而減少對樣本集進行分類處理的數據量，提高算法的運算效率.通過對不同的數據集進行測試表明，本文提出的算法有利于提高大樣本集的分類的效率，降低運算時間的消耗，同時也提高了分類結果的準確率.

[1] 閆永剛， 馬廷淮， 王 建. KNN分類算法的MapReduce并行化實現[J]. 南京航空航天大學學報， 2013，45(4):550-555．

[2] 劉應東， 牛惠民. 基于k-最近鄰圖的小樣本KNN分類算法[J]. 計算機工程， 2011，37(9):198-200．

[3] 陳海彬， 郭金玉， 謝彥紅. 基于改進K-means聚類的kNN故障檢測研究[J]. 沈陽化工大學學報， 2013，27(1):69-73．

[4] 羅賢鋒， 祝勝林， 陳澤健， 等. 基于K-Medoids聚類的改進KNN文本分類算法[J]. 計算機工程與設計， 2014，35(11):3864-3867,3937．

[5] 耿麗娟， 李星毅. 用于大數據分類的KNN算法研究[J]. 計算機應用研究， 2014，31(5):1342-1344,1373．

[6] BHATTACHARYA G， GHOSH K， CHOWDHURY A S. An affinity-based new local distance function and similarity measure for KNN algorithm [J]. Pattern Recognition Letters， 2012，33(3):356-363．

[7] SU M Y. Using clustering to improve the KNN-based classifiers for online anomaly network traffic identification [J]. Journal of Network & Computer Applications， 2011，34(2):722-730．

[8] 夏竹青. 基于不均衡數據集和決策樹的入侵檢測分類算法的研究[D]. 安徽:合肥工業大學， 2010．

[9] GAO Y， GAO F. Edited AdaBoost by weighted kNN [J]. Neurocomputing， 2010，73(18):3079-3088．

[10] 王永貴， 李鴻緒， 宋 曉. MapReduce模型下的模糊C均值算法研究[J]. 計算機工程， 2014，40(10):47-51．

[11] 文傳軍， 汪慶淼， 詹永照. 均衡模糊C均值聚類算法[J]. 計算機科學， 2014，41(8):250-253．

[12] 周世波， 徐維祥， 柴 田. 基于數據加權策略的模糊C均值聚類算法[J]. 系統工程與電子技術， 2014，36(11):2314-2319．

[13] HAVENS T C， BEZDEK J C， LECKIE C， et al. Fuzzy C-means algorithms for very large data [J]. IEEE Transactions on Fuzzy Systems， 2012，20(6):1130-1146．

ImprovedKNNclassificationalgorithmbasedonFuzzyC-Means

ZHU Fubao, XIE Lijie, TANG Mengmeng, ZHU Haodong

(School of Computer and Communication Engineering, Zhengzhou University of Light Industry, Zhengzhou 450002, China)

KNN algorithm is a classification algorithm that is simple and easy to implement, but when the training set is rather big and features are more, its efficiency is low with which takes more time. To solve this problem, an improved KNN classification algorithm was proposed based on Fuzzy C-Means. The improved algorithm introduces the theory of Fuzzy C-Means based on the traditional KNN classification algorithm. Through processing the sample data clustering, the formation of sub clusters substitutes all the sample set of the sub cluster, which helps reduce the number of training set. Thereby the workload of the KNN classification process is reduced, with the classification efficiency improved and the KNN algorithm better applied in data mining. The theoretical analysis and experimental results show that this method is able to significantly improve the efficiency and accuracy of the algorithm when dealing with large data, meeting the demand of processing data.

Fuzzy C-Means; clustering; KNN classification

2017-02-22.

河南省科技攻關項目(162102210146；162102310579);河南省教育廳科學技術研究重點項目(13A52036); 河南省高等學校青年骨干教師資助計劃項目(2014GGJS-084); 鄭州輕工業學院校級青年骨干教師培養對象資助計劃項目(XGGJS02); 鄭州輕工業學院博士科研基金資助項目(2010BSJJ038).

*通訊聯系人. E-mail: zhuhaodong80@163.com．

10.19603/j.cnki.1000-1190.2017.06.005

1000-1190(2017)06-0754-06

TP311.13

A