時間尺度上非保守系統的Lie對稱性及其守恒量

林 魏， 朱建青

(蘇州科技大學 數理學院， 江蘇 蘇州 215009)

時間尺度上非保守系統的Lie對稱性及其守恒量

林 魏， 朱建青*

(蘇州科技大學 數理學院， 江蘇 蘇州 215009)

研究了時間尺度上非保守系統的Lie對稱性及其守恒量.首先，基于時間尺度上微分方程在無限小變換下的不變性，導出了時間尺度上Lie對稱性的確定方程；然后，建立了時間尺度上非保守系統的Lie對稱性的結構方程，以及時間尺度上非保守系統的Lie對稱性的Noether型守恒量；最后，舉例說明其結果的應用.

時間尺度; 非保守系統; Lie對稱性; 守恒量

對稱性和守恒量理論的研究是現代數理科學中的一個重要研究領域，也是分析力學近代發展中的一個重要方向.1979年Lutzky等人給出了分析力學中Lie對稱性[1]，主要闡述了微分方程在無限小變換群作用下，具有不變性.此后，Lie對稱性在動力學系統中有了廣泛的研究[2-11].但是隨著社會生產的實際需要，經典力學系統已不能滿足實際問題.

1988年Stefan Hilger提出了時間尺度上的微積分理論[12]，這種獨特的理論有效的將離散系統和連續系統的研究統一了起來，并且該理論不僅在物理學、最優控制、工程等領域中有廣泛的應用[13-18]，還在分析力學的研究中吸引了廣大學者的關注[19-23].對于時間尺度上微積分理論的研究，國內外學者分別展現了自己的研究成果.如，2004年，Bohner研究了Eluer-lagrange方程在時間尺度上的表達形式及時間尺度上的偏微分問題[24-25]；2008年，Bartosiewicz和Torres將Noether對稱性推廣到了時間尺度上[26]；2010年詹再東和韋維研究了時間標度上的Taylor公式及鏈式法則[27]；2011年Bartosiewicz等學者進一步研究了時間尺度上二階Eluer-lagrange方程變分問題[28]；2013年蔡平平在他的碩士論文時間坐標上約束力學系統的對稱性理論研究中提出了Lie對稱性的研究[29].至此，對于時間尺度上Lie對稱性的研究剛剛起步，本文試圖對時間尺度上非保守系統的Lie對稱性及其守恒量的研究進行些探討.

1 時間尺度上微分方程的不變性

文中所涉及時間尺度上的微積分理論的定義及其有關性質請參閱文獻[13].

對于時間尺度上Lie對稱性的研究是基于微分方程在無限小變換下的不變性為出發點的.下面將從時間尺度上一階微分方程和二階微分方程在無限小變換下的不變性進行討論.

1.1 時間尺度上一階微分方程的不變性

假設時間尺度T上一階微分方程表示為

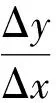
(1)

取無限小變換為

x*=x+εξx，y，y*=y+εηx，y.

(2)

如果有

(3)

則稱方程(3)相對于方程(1)是在時間尺度上的保形不變的，其中Gx，y為保形因子，

根據式(3)得到

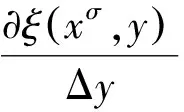
(4)

方程(4)稱為時間尺度上微分方程在無限小變換下的確定方程.

1.2 時間尺度上二階微分方程的不變性

討論時間尺度T上二階微分方程

(5)

在無限小變換下的不變性.問題轉化為如下兩個一階微分方程

ν-Δy=0，Δν-fx，y，ν=0，

(6)

的不變性，其中

(7)

取無限小變換

(8)

則

于是令

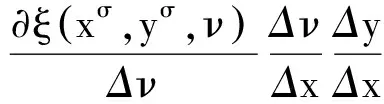
(9)

又有

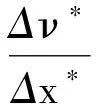
(10)

在變換(8)下，方程(6)的第二個保持不變，有

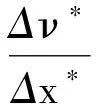
(11)

現將式(10)代入式(11)中，并展開f，得

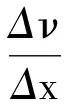
由時間尺度上保形不變性得

(12)

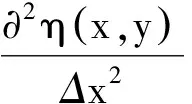
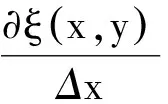
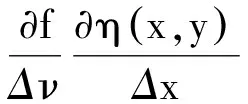
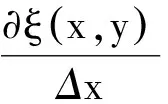
(13)

方程(13)稱為系統的確定方程.

2 時間尺度上Lagrange系統的運動方程

設力學系統的位形由n個廣義坐標qss=1，2，…，n確定，時間尺度T上非保守Lagrange系統的運動方程為

(14)

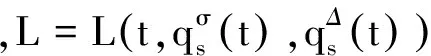
(15)

將方程(14)展開，可求出所有的廣義加速度，簡記為

(16)

3 時間尺度上Lie對稱性的無限小變換與生成元

取時間t和廣義坐標qss=1，2，…，n的無限小單參數變換群

(17)

其中，ε為小參數，ξ0，ξs為無限小變換的生成元.

引入無限小生成元向量

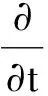
(18)

其一次擴展

(19)

以及它的二次擴展

(20)

根據微分方程在無限小變換下的不變性理論知，方程(16)在無限小變換(17)下的不變性表為

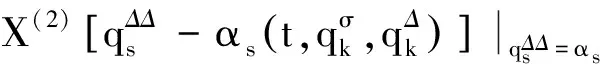
(21)

它可表為

s=1，2，…，n.

(22)

稱方程(22)為方程(16)的確定方程.

定義如果無限小變換(17)的生成元ξ0，ξs滿足確定方程(22)，則稱對應的對稱性為時間尺度上非保守Lagrange系統的Lie對稱性.

4 結構方程與守恒量

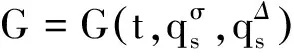
(23)

則非保守系統(14)存在如下形式守恒量

(24)

證明

如果T=，則σt=t，μt=0，于是式(23)給出了經典的非保守力學系統的Lie對稱性的結構方程[3]

(25)

而守恒量(24)也成為經典的非保守力學系統的Lie對稱性的Noether型守恒量

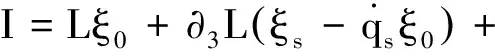
(26)

5 算例

定義時間尺度T=2n:n∈∪0，假設廣義力系統的Lagrange函數為

(27)

受到的非保守力為

(28)

首先，由(14)式可得系統的運動微分方程為

(29)

(30)

其次，建立時間尺度上Lie對稱性的確定方程并求解.由確定方程(22)可得

(31)

(32)

方程(31)和(32)的解為

ξ0=0，ξ1=t，ξ2=1.

(33)

然后，建立時間尺度上Lie對稱性的結構方程，并求解規范函數.由結構方程(23)得

(34)

由方程(34)可得

(35)

最后，求Lie對稱性導致的Noether型守恒量，將方程(35)代入守恒量(24)中得

(36)

如果T=，σt=t，μt=0時，由式(26)知，系統有如下守恒量

(37)

6 結論

本文基于時間尺度上微積分理論，結合變分原理與Taylor展開方法，研究了非保守力學系統的Lie對稱性.最終，得到了時間尺度上非保守系統的Lie對稱性的確定方程、結構方程與守恒量，建立了時間尺度上非保守系統的Lie對稱性的Noether型守恒量.當μt=0時，該文結果可退化到連續系統下的Lie對稱性.因此，本文更具一般性，其思想方法可推廣到時間尺度上非完整系統的Lie對稱性等的研究中.

[1] LUTZKY M. Dynamical symmetries and conserved quantities [J]. J Phys A: Math Gen， 1979，12(7):973-981．

[2] 梅鳳翔. 李群和李代數對約束力學系統的應用[M]. 北京: 科學出版社， 1999．

[3] 趙躍宇. 非保守力學系統的 Lie 對稱性和守恒量[J]. 力學學報， 1994，26(3):380-384．

[4] 梅鳳翔. 尚玫. 一階Lagrange系統的Lie對稱性與守恒量[J]. 物理學報， 2000，49(10):1901-1903．

[5] 梅鳳翔. 包含伺服約束的非完整系統的Lie對稱性與守恒量[J]. 物理學報， 2000，49(7):1207-1210．

[6] 張 毅， 梅鳳翔. 單面完整約束力學系統的Lie對稱性研究[J]. 科學通報， 2000，45(4):353-356．

[7] FU J L， CHEN X W， LUO S K. Lie symmetries and conserved quantities of rotational relativistic systems [J]. Applied Mathematics and Mechanics， 2000，21(5):549-556．

[8] 張 毅. Birkhoff系統的一類Lie對稱性守恒量[J].物理學報， 2002，51(3):0461-0464．

[9] 梅鳳翔. 約束力學系統的對稱性與守恒量[M]. 北京: 北京理工大學出版， 2004．

[10] LUO S K. New types of Lie symmetries and conserved quantities for a relativistic Hamilton system [J]. Chinese Physics Letters， 2003，20(5):597-599．

[11] 張孝彩，張毅.基于分數階模型的完整非保守系統的Lie對稱性與守恒量[J].蘇州科技學院學報(自然科學版)， 2016，33(2):8-13．

[12] HILGER S. Ein Masskettenkalku Anwendung auf Zentrumsmannigfaltigkeiten [D]. Würzburg: Universif?t Würzburg， 1988．

[13] BOHNER M， PETERSON A. Dynamic equations on time scales: an introduction with applications [M]. Bostion: Birkh?user， 2001．

[14] AGARWAL R P， O’REGAN D. Nonlinear boundary value problems on time scales [J]. Nonlinear Analysis， 2001，44(4):527-535．

[15] SAKER S H. Oscillation of nonlinear dynamic equations on time scales [J]. Applied Mathematics and Computation， 2004，148(1):81-91．

[16] AGARWAL R P， BOHNER M. Basic calculus on time scales and some of its applications [J]. Results Math， 1999，35(1-2):3-22．

[17] AGAWAL R P， BOHNER M O， O’REGAN D， et al. Dynamic equations on time scales: a survey [J]. Comput Appl Math， 2002，141(1-2):1-26．

[18] GIREJKO E， MALINOWSKA A B， TORRES D F M. Delta-nabla optimal control problems [J]. Journal of Vibration and Control， 2010，17(11):999-1005．

[19] CAI P P， FU J L， GUO Y X. Noether symmetries of the nonconservative and nonholonomic system on time scales [J]. Sci China: Phys Mech Astron， 2013，56(5):1017-1028．

[20] 張 毅. 時間尺度上Hamilton系統的Noether理論[J]. 力學季刊， 2016,37(2)， 214-224．

[21] SONG C J， ZHANG Y. Noether theorem for Birkhoffian systems on time scales [J]. J Math Phy， 2015，56(10):102701(1-7)．

[22] ZU Q H， ZHU J Q. Noether theorem for nonhonomic nonconserative mechanical syetems in phase spacs on time scales [J]. Journal of Mathematical Physics， 2016，57(10):082701(1-4)．

[23] 祖啟航， 朱建青， 宋傳靜. 時間尺度上相空間中非Chetaev型非完整系統的Noether理論[J]. 華中師范大學學報(自然科學版)， 2017，51(1):23-27．

[24] BOHNER M， GUSEINOV G S. Partial differentiation on time scales [J]. Dyn Syst Appl， 2004，13(3):351-379．

[25] BOHNER M. Calculus of variations on time scales [J]. Dyn Syst Appl， 2004，13(12):339-349．

[26] BARTOSIEWICZ Z， TORRES D F M. Noether’s theorem on time scales [J]. Math Anal Appl， 2008，342(2):1220-1226．

[27] 詹再東， 韋 維. 時間標度上的Taylor公式及鏈式法則[J]. 數學的實踐與認識， 2010，40(7):199-204．

[28] BARTOSIEWICZ Z， MARTINS N， TORRES D F M. The second Euler-Lagrange equation of variational calculus on time scales [J]. European Journal of Control， 2010，17(1):9-18．

[29] 蔡平平. 時間尺度上約束力學系統的對稱性理論研究[D]. 杭州： 浙江理工大學， 2012．

Liesymmetryandconservedquantityfornon-conservativesystemsontimescales

LIN Wei, ZHU Jianqing

(College of Mathematics and Physics, Suzhou University of Science and Technology, Suzhou, Jiangsu 215009, China)

In this paper, Lie symmetry and conserved quantity for non-conservative systems on time scales are studied. Firstly, based on the invariance of the differential equations on time scales under the infinitesimal transformations of groups, the determining equations of Lie symmetry on time scales are provided. Secondly, the structure equations of Lie symmetry for non-conservative systems on time scales are established, and formulation of the Noether conserved quantity is constructed. Finally, an example is presented to illustrate the application of the results.

time scales; non-conservative systems; Lie symmetry; conserved quantity

2017-05-12.

國家自然科學基金資助項目(11572212)；蘇州科技大學研究生科研創新計劃項目(SKCX16_057)．

*通訊聯系人. E-mail: zjq@mail.usts.edu.cn.

10.19603/j.cnki.1000-1190.2017.06.008

1000-1190(2017)06-0772-05

O316

A