地震數據去噪的研究與分析

崔少華，方振國，姜恩華

（淮北師范大學，安徽淮北 235000）

地震數據去噪的研究與分析

崔少華，方振國，姜恩華

（淮北師范大學，安徽淮北 235000）

小波分解利用信號和噪聲在時頻域內小波系數差異，重構信號從而去除噪聲；SVD算法利用信號和噪聲奇異值的差異，選取合適的空間維數重構信號從而去除噪聲。通過模型驗證對比了兩種算法的去噪效果和優缺點，發現小波算法對水平同相軸和傾斜同相軸具有相同的去噪效果，但運算時間較長；SVD算法對水平同相軸去噪效果很好，對于傾斜同相軸幾乎不能去噪，但運算時間較短。

小波分解；SVD算法；水平同相軸；傾斜同相軸

0 引言

實際中采集到的地震數據通常混入大量隨機噪聲，幾乎不可避免，因此對地震數據進行隨機噪聲壓制往往是處理數據的首要工作。小波分解去噪是在時頻域內處理信號，而SVD則是在時域內處理信號。本文主要針對上述兩種去噪方法進行探討和分析，從而歸納兩種算法的優缺點。

1 小波分解與重構去噪法

1.1 基本原理

小波變換顯示的是信號的局部特性，通過伸縮和平移等運算將信號進行多尺度細化分析[1]（Multiscale Analysis）。小波分解與重構去噪法是利用小波變換根據實際需要，將信號（含噪聲）分解到同一個尺度下，得到一系列處于不同頻帶的小波系數（一般認為高頻部分對應信號，低頻部分對應噪聲）。通過將噪聲所在頻帶置為零，再進行小波重構，從而達到去噪的效果[2]。

假設fk是f（t）的采樣數據，即fk=c0,k（零尺度空間小波系數），則可將信號f（t）的正交小波變換分解的公式[3]寫為：

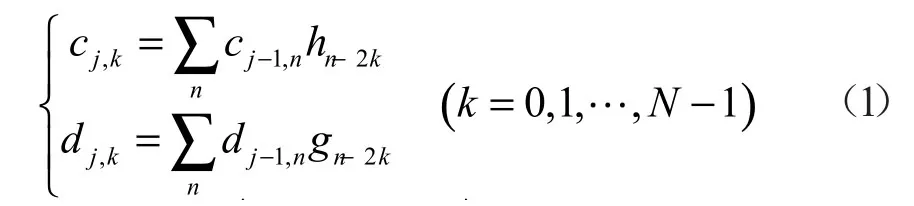
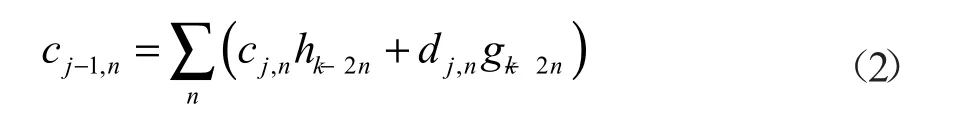
1.2 模型驗證

構成1個二維地震記錄：總共200道，每道501個采樣點，采樣間隔1毫秒，其中一條水平同相軸，一條傾斜同相軸。地震子波采用峰頻為50Hz的Ricker子波，每道數據加入幅度為0.1的隨機噪聲，如圖1所示。對原始數據進行小波分解與重構，去噪結果如圖2所示，噪聲如圖3所示。

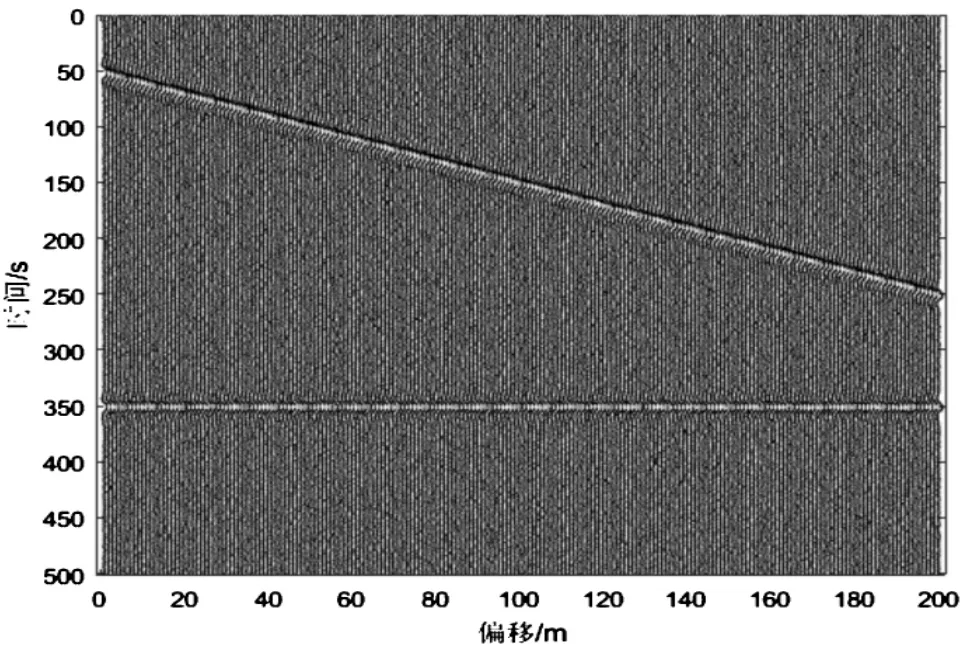
圖1 含噪原始數據

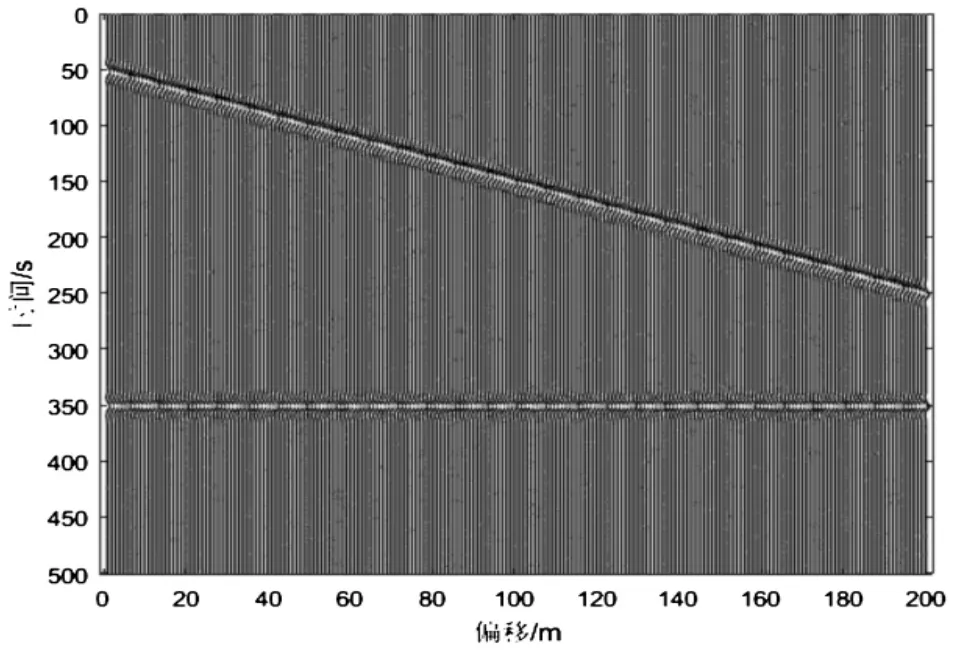
圖2 小波重構有效信號

圖3 小波分解去除噪聲

由圖2可知，小波分解算法可以將混合數據中的大量隨機噪聲進行壓制，對于傾斜同相軸也可以達到很好的去噪效果。但由圖3可知，去除的噪聲中還含有部分信號的能量，這是由于小波分解時采用的Symmlet8小波算子進行8尺度分解，在重構時對信號有一定損傷。可見小波分解算法只要選取合適的小波分解算子，即可達到理想的去噪效果。

2 SVD分解去噪算法

2.1 SVD原理

假設地震記錄為m×n的數據矩陣X，其中m表示地震波通道觀察個數，n表示每個通道上的采樣點數。將矩陣X做分解變換為[6]：

式（3）中U與V均為正交歸一陣，∑為準對角矩陣，在m＜n的情況下，有

一般設 σ1≥σ2≥...≥σm≥0，稱 σi為數據的 X奇異值。

式中ui和vi稱為左、右奇異矢量[7]，其維數分別為m×1和n×1。

因此，維數為m×n的原始數據就被分解成維數相同的m個子矩陣，這就是奇異值分解[8]。

確定有效信號空間維數p，進行選擇前p個本征圖像來進行重構就可以恢復有效信號：

SVD分解算法在去噪時的關鍵是對有效信號進行重構，所選取的重構信號維數p，即加權本征圖像的個數，對于去噪結果有很大的影響[9]。若選用p的維數小于有效信號的維數，則無法重構信號且在去除噪聲中包含信號能量，即對信號有損傷；若選用p的維數大于信號的維數，則會引入過多的隨機噪聲，在重構的信號中含有大量噪聲未被壓制，去噪效果不佳。因此重構維數p的選擇是SVD算法的關鍵。

2.2 模型驗證

采用圖1的含噪原始數據進行SVD分解，由于數據中同相軸僅含有兩種傾角，因此重構維數p=2，重構結果如圖4所示，噪聲如圖5所示。

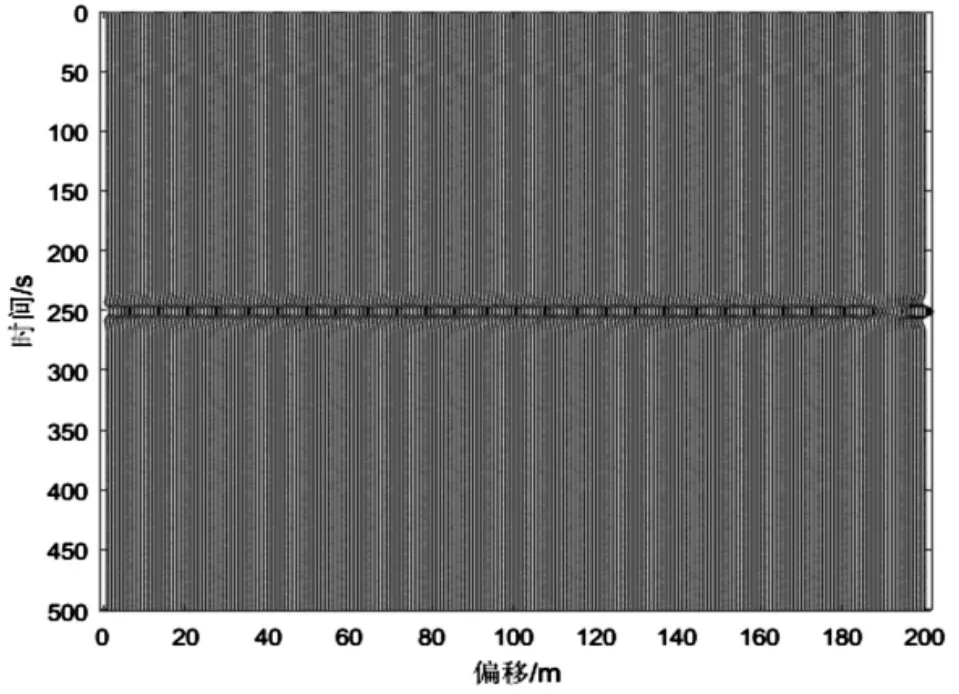
圖4 SVD重構有效信號

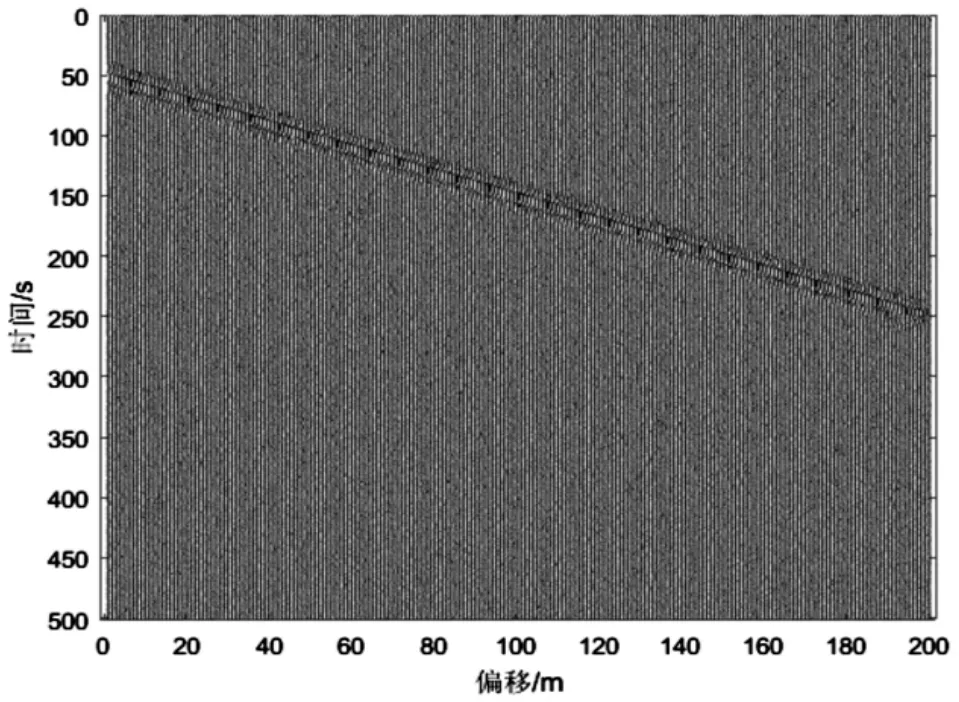
圖5 SVD去除噪聲

由圖4可知，SVD重構信號中只含有水平同相軸，不含有任何傾斜同相軸，這是由于SVD算法是在時域進行分解，利用各道數據之間的相關性將地震記錄分解成奇異值并按序排列，信號的有效性越強，分解出奇異值差異越明顯[10]，越利于提取信號的奇異值進行重構去噪。由于傾斜同相軸各道的相關性減弱（傾角越大，相關性越弱），因此SVD算法無法對其進行重構。從圖5很明顯地看出，傾斜同相軸完全沒有被重構，噪聲中卻不含有任何水平同相軸的能量，所以SVD時域分解對傾斜同相軸有嚴重的損害。

3 小波算法與SVD算法的對比

3.1 PSNR的對比

采用圖像的峰值信噪比（Peak Signal to Noise Ratio，PSNR）對兩種算法對比，結果如表1所示。

表1 兩種算法PSNR對比

由表1可知，小波分解算法的PSNR高出SVD算法的接近8dB，這說明前者還原圖像的程度高于后者，即前者的去噪效果優于后者的去噪效果。

3.2 去噪時間的對比

在實際中往往處理的是大規模地震記錄，因此對于處理時間的要求同樣嚴格。將兩種算法的去噪時間進行對比（基于驗證模型），結果如表2所示。

表2 兩種算法去噪時間對比

3.3 去噪效果的對比

小波算法在分解和重構信號時對有效信號和噪聲采用同一個分解尺度，因此對水平同相軸和傾斜同相軸去噪效果相同（圖2），同時小波分解算法對于傾斜同相軸具有良好的去噪效果（圖3）。

SVD算法對水平同相軸的去噪效果最佳（圖4），對傾斜同相軸幾乎不能去噪（圖5）。

4 總結

綜上所述，小波分解算法和SVD算法各有優缺點，決定小波分解算法去噪效果的關鍵因素是小波算子分解尺度的選取，分解尺度越大，去噪越明顯。但尺度選取過大，在去噪時會引入過多隨機噪聲，反而會使去噪效果下降。

決定SVD算法去噪效果的關鍵因素是重構維數的選取，且重構信號維數的取值需人工判斷，在大數據量的地震記錄中，每個頻率切片上對重構維數均需進行判斷和選取。

［1］王香云.基于信號去噪的小波算法研究［J］.太原師范學院學報（自然科學版），2015，14（1）：33-37.

［2］王超，沈斐敏.小波變換在探地雷達弱信號去噪中的研究［J］.物探與化探，2015，39（2）：421-424.

［3］崔少華，單巍.基于小波分析的地震資料去噪方法的研究和應用［J］.淮北師范大學學報（自然科學版），2016，37（3）：43-46.

［4］蔡正保.一種基于混沌加密和小波變換的數字水印技術研究［J］.廊坊師范學院學報（自然科學版），2016，16（2）：17-21.

［5］謝斌，樂鴻浩，陳博.一種基于小波去噪的DF T信道估計改進算法［J］.計算機工程與科學，2016，38（9）：1790-1796.

［6］崔業勤，高建國，丁國超.L L E重構和SVD分解的地震信號降噪方法［J］.計算機工程與應用，2016，52（15）：266-270.

［7］李目，何怡剛，吳笑鋒，等.基于奇異值分解的分數階小波綜合實現方法［J］.電子測量與儀器學報，2016，30（2）：241-248.

［8］唐炬，董玉林，樊雷，等.基于Hankel矩陣的復小波-奇異值分解法提取局部放電特征信息［J］.中國電機工程學報，2015，35（7）：1808-1817.

［9］邢琮琮，吳燕岡，趙昕，等.奇異值分解（SVD）在位場數據去噪中的應用［J］.世界地質，2016，35（4）：1119-1126.

［10］Thind D K，Jindal S.A Semi Blind DWT-SVD Video Watermarking［J］.Procedia Computer Science，2015，46（2）：1661-1667.

Research and Analysis of Seismic Data Denoising

CUI Shao-hua,FANG Zhen-guo,JIANG En-hua
（Huaibei Normal University，Huaibei 235000，China）

The wavelet decomposition uses the difference of signal and noise in the time-frequency domain wavelet coefficient，then reconstructs the signal wiping off noise；SVD algorithm uses the difference of the signal and noise singular value，selecting the appropriate dimensions to reconstruct the signal wiping off noise.Through the comparison of two kinds of model validation algorithm for denoising effect，we know that wavelet algorithm for level phase axis and dip phase axis has the same denoising effect，but the operation time is long.The SVD algorithm for level event denoising effect is very good and the operation time is short，but it does not fit for dip event axis denoising.

wavelet decomposition；SVD algorithm；horizontal event；dip event

P315

A

1674-3229（2017）04-0033-03

2017-07-16

安徽省高等學校自然科學研究項目（KJ2017B008）；淮北師范大學質量工程項目（jy2016133）

崔少華（1983-），女，碩士，淮北師范大學物理與電子信息學院講師，研究方向：電子與通信。