大學生數學課程與建模的契合點

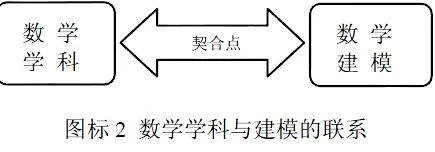
大學生數學課程與數學建模，表面上看二者存在著必然聯系，但是，實際上，兩者之間的關系很微妙。主要表現在，數學水平和建模能力之間沒有明的對應關系。個別有些數學成績很優秀的同學，建模成績不一定也優秀，反過來，數學成績不好的同學，建模能力也可能不差。本文通過二者的關系分析，力爭找到它們之間的契合點，從而相互促進，相得益彰。

一、數學知識對建模思想的滲透。從本質上來說，數學知識本身，就是建模的結果。因為，數學本身就是來自于現實生活，數學理論本身就是服務于社會實踐的，離開了實際背景，數學不會孤立存在的。例如，算籌起源于原始人的狩獵需求，幾何起源于對現實生活的直觀描述（長度、面積、容積等）。但是，實際上，我們在接觸數學知識的時候，往往忽略了它本身的實際意義，單純的去認知，從而養成了數學是抽象概念的思維模式。為此，在數學課程方面，我們應該努力做到以下幾點：

1.牢固樹立數學來自于生活，反過來又服務于生活的基本理念。例如，劉輝的割圓術滲透著極限思想，不規則圖形中隱含著規則圖形，導數可以看做是極限思想的巧妙運用，定積分可以認為是無窮小求和最直接的體現，函數就是變量之間的彼此依存關系，函數表達式就是這種關系的數學模型，而線性代數是線性變量的求解平臺，概率論又是預測學的基礎模塊。

2.建立數學知識點與現實生活及時對接的思維模式。數學學習中，對基本概念，基本定理和基本公式，盡量的對接它們在現實生活中的應用。例如，一次函數與直線，二次函數與拋物曲線，雙曲線與發電廠冷卻塔的側面線，橢圓跟天體運動的軌道線，極限跟無限分割，導數跟光滑曲線，等等。

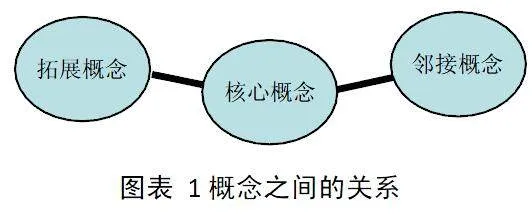
3.抽象概念的應用節點。越是呈現抽象的概念，越要善于尋找它的應用點，盡可能的找到對應實例，使得抽象概念盡可能的具體化。先讓我們看下圖：

圖中不難看出，核心概念鄰接著其它概念，然后就是概念的拓展效應。如定積分的概念本身，就含有若干鄰接概念：連續，分割，和式，極限等等。 給定積分概念做出具體描述，就是概念本身在幾何上對接著不規則圖形的面積、長度、體積等的計算。在物理學上，往往對接著從加速度到速度，再從速度到距離之間的反求關系。

4.數學模型化思維模式的轉變。對待新的數學概念，我們要樹立數學模型化思維模式。如，一元變量方程可以視為一元數學模型，二元方程可以視為二元數學模型，多元方程可以視為多元數學模型。許多函數表達式可以看做是特定意義下的目標函數模型，變量對應的約束不等式可以視為約束條件模型，等等。只要我們建立了這種思想就很容易建立數學概念與數學模型的聯系。

二、數學建模對數學學科的正向促進。從數學建模的基本規律上來看，它自身是來自于現實生活中急需解決而又不容易解決的問題的實際應用。數學建模自身難度是不小的，除了對數學知識本身有一定要求以外，更多的是依賴思維靈感，或者是解決問題的突發奇想。這就決定了建模本身對數學學科具備了良好的正面帶動和促進作用。讓我們從一下幾方面進行分析。

1.數學建模需要比較扎實的基本功和基本技能。例如，除了數學概念本身的熟練程度以外，還需要具備有關數學應用軟件的使用基本技能。例如，matlab ，lingo，excel，數據庫，spss數據處理軟件的使用，等等。當然，數學基本知識點的要求并沒有很高，基本夠用即可。但是，反過來，如果數學基本知識點不全面，需要時想不到也不會用，會影響建模的完成。

2.數學建模需要具備突發靈感。所謂突發靈感，就是在實際問題應用中，能快速的把實際問題和它所蘊含的數學知識點相對接。在對接中找到模型函數表達式和約束條件，使兩者盡可能的相互貼近，不斷優化。例如，在建模給出的實際問題中，我們通常要首先分析變量性質，根據變量性質，給出變量所滿足的約束條件和目標函數。在某些靈感的引導下不斷的優化，不斷的模擬，最終獲得比較理想的結果。

3.數學建模需要雙向思維模式。所謂雙向思維模式，就是從實際問題到數學模型，再從數學模型到實際問題，能實現快速轉換。有些時候我們的思維模式，往往是單向的，不可逆的，這正是我們傳統思維模式的弊端所在。例如，演繹推理和歸納推理的不同模式，很多人會不適應。盡管如此，這種雙向模式的效用是革命性的，它會較大的拓展我們的思維空間。

綜上所述，數學課程與數學建模之間，存在著相互促進，又相互依賴的密切聯系。這種依賴不是因果性的，而是寬松型的。數學學科的優秀不代表數學建模成績的同步優秀，反之亦然。但是，如果我們能處理好二者之間的微妙關系，可以大大促進兩者的交互發展。平時學習中，我們要養成數學模型化，數學知識實際化的思維習慣，反過來，數學模型又反向促進了數學知識本身的豐富和提高。

（作者單位：山東職業學院）