基于FastICA的低信噪比探地雷達信號去噪

戴前偉， 成沁宇， 馮德山

(1.中南大學(xué) 地球科學(xué)與信息物理學(xué)院,長沙 410083；2.中南大學(xué) 有色金屬成礦預(yù)測與地質(zhì)環(huán)境監(jiān)測教育部重點實驗室，長沙 410083)

基于FastICA的低信噪比探地雷達信號去噪

戴前偉1，2， 成沁宇1，*， 馮德山1，2

(1.中南大學(xué) 地球科學(xué)與信息物理學(xué)院,長沙 410083；2.中南大學(xué) 有色金屬成礦預(yù)測與地質(zhì)環(huán)境監(jiān)測教育部重點實驗室，長沙 410083)

在背景條件復(fù)雜的工區(qū)，為了提高探地雷達(GPR)勘探資料解釋的準(zhǔn)確性和可靠性，利用獨立分量分析理論進行了強噪聲背景下的探地雷達信號去噪研究。闡述獨立分量分析(ICA)基本理論，著重討論了基于負(fù)熵最大化的快速獨立分量分析(FastICA)算法。應(yīng)用FastICA算法對單道探地雷達數(shù)據(jù)和正演含噪雷達剖面分別進行去噪分析，得到去噪后的探地雷達信號。以湖北恩施彭家寨隧道GPR實測數(shù)據(jù)為例，將Fast ICA算法應(yīng)用于探地雷達剖面數(shù)據(jù)去噪。研究結(jié)果表明,將FastICA算法應(yīng)用于探地雷達信號處理，擺脫了傳統(tǒng)方法參數(shù)設(shè)置的束縛，流程簡單，在GPR去噪方面有獨特的優(yōu)勢，可較好地對低信噪比的GPR原始數(shù)據(jù)進行噪聲去除，有助于突出探地雷達剖面中異常體特征，達到了提高資料解釋準(zhǔn)確性和可靠性的目的。

獨立分量分析； 探地雷達； 負(fù)熵； FastICA算法； 噪聲去除

0 引言

探地雷達是一種利用地下介質(zhì)的不連續(xù)性來探測地下目標(biāo)的有效工具。憑借其具有探測速度快、探測周期短、探測過程連續(xù)、操作方便靈活等優(yōu)點，在地質(zhì)勘探、城市建設(shè)、國防安全、公路、鐵路、機場、隧道、考古等許多領(lǐng)域都表現(xiàn)出強勁的生命力和廣闊的應(yīng)用前景[1]。由于實際測量過程中，受到地面高低起伏、地下介質(zhì)不均勻、采集系統(tǒng)內(nèi)部噪聲干擾等各方面因素的干擾，使得探地雷達信號分辨率受到較大影響，給資料的準(zhǔn)確解釋和異常體的精確定位帶來了很大困難。目前傳統(tǒng)的去噪方法主要有：傅立葉變換、加窗傅立葉變換[2]、S變換[3]、小波變換[4]、小波-KL變換[5]、希爾伯特-黃變換[6]等。近年來小波變換被廣泛應(yīng)用于信號處理領(lǐng)域，其中以小波閾值去噪應(yīng)用最為廣泛，但其不足的地方在于具體小波閾值函數(shù)、軟硬閾值、尺度系數(shù)的選擇對去噪結(jié)果影響較大，同時對于非連續(xù)信號，采用小波閾值去噪后容易產(chǎn)生偽吉布斯現(xiàn)象[7]，這些問題制約了小波變換在探地雷達信號去噪中的應(yīng)用和推廣。因此，有必要引入一種更適應(yīng)的方法來去除探地雷達信號中的噪聲干擾，以提高資料的分辨率。

1 獨立分量分析基本理論

獨立分量分析(Independent Component Analysis ,ICA)是近十幾年發(fā)展起來的盲源分離理論中的一種統(tǒng)計學(xué)方法[8]。ICA的基本思路是以高階統(tǒng)計量為基礎(chǔ)，遵循統(tǒng)計獨立的原則，采用優(yōu)化算法將觀測信號分離成若干獨立分量，認(rèn)為分離出來的獨立分量是對源信號的近似估計[9]。

圖1 ICA線性模型Fig.1 ICA linear model

1.1 ICA模型

ICA的線性組合模型中，s1(t)、s2(t)、…、sn(t)是n個符合獨立、非高斯分布的源信號；x1(t)、x2(t)、…、xm(t)是m個觀測信號；y1(t)、y2(t)、…、yn(t)為n個源信號的近似解(圖1)。

Y=W×X=W×A×S

(1)

為了使Y更接近于源信號S，則必須使W×A=I。ICA的目的就是在事先不知道獨立信號源s(t)和混合矩陣A的情況下，尋找一個分離矩陣W=A-1[10]。利用獨立分量分析解決上述問題的關(guān)鍵在于兩點：①選擇合適目標(biāo)函數(shù)作為衡量分離結(jié)果非高斯性的依據(jù)；②尋找一種高效的優(yōu)化算法來求解分離矩陣W，當(dāng)某個分離矩陣W能夠使目標(biāo)函數(shù)達到極值，則該分離矩陣W為所求。優(yōu)化算法的目的是為了得到分離矩陣W的修正量，并進行優(yōu)化。筆者采用基于負(fù)熵最大化的快速獨立分量,分析算法進行研究。

1.2 基于負(fù)熵最大化的非高斯性判斷依據(jù)

負(fù)熵是基于信息論中熵的概念提出的，是衡量信號非高斯性的一個相對理想?yún)?shù)。但因為y的概率分布事先無法預(yù)知，所以實際中采用式(2)的近似計算方法[11]：

J(y)∝[E{G(y)}-E{G(ygauss)}]

(2)

其中：函數(shù)G表示非二次型函數(shù)；ygauss表示具有零均值、單位方差的Gauss隨機變量。常用的函數(shù)G有：

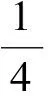
(3)

2 FastICA算法的實現(xiàn)

為了使J(y)∝[E{G(y)}-E{G(ygauss)}]最大化，獲得最優(yōu)的E{G(y)}。根據(jù)Kuhn-Tucker條件，在E{(WTx)2}=‖W‖2=1時，最優(yōu)值在滿足下列條件的各點得到[12]：

E[xg(WTx)]-βx=0

(4)

其中：β是拉格朗日乘子；函數(shù)g是函數(shù)G的一階導(dǎo)數(shù)。利用牛頓迭代法求解式(4)，可得到下面近似的牛頓迭代格式。

W+=E[xg(WTx)]-E[g(WTx)]W

(5)

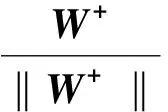
(6)

FastICA算法大體上分為兩步：①對觀察信號進行中心化、白化等預(yù)處理過程，預(yù)處理過程使觀察信號符合獨立分量分析對數(shù)據(jù)零均值、獨立、非高斯性的要求；②計算最優(yōu)的分離矩陣W，提取各個分量[13]。圖2給出了多元FastICA算法的基本流程。

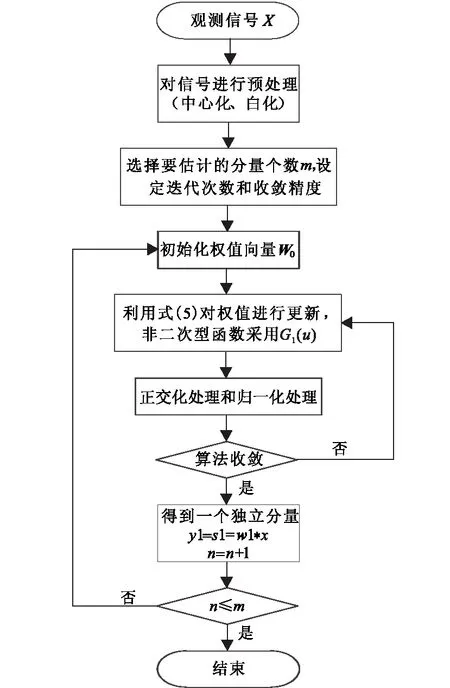
圖2 多元FastICA算法的基本流程Fig.2 Basic processes of FastICA algorithm

為了衡量FastICA算法的分離性能，引入A.Paraschiv-Ionescu等[14]提出的性能函數(shù)PI(performanceindex):

(7)

和相關(guān)系數(shù)ρ:

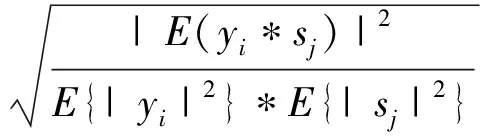
(i，j=1,2,…,N)

(8)

性能函數(shù)PI中的矩陣C為分離矩陣W和混合矩陣A的乘積，cij為矩陣C的第(i,j)個元素。從式(7)可以看出，PI的實質(zhì)就是計算分離矩陣W和混合矩陣A的乘積與單位矩陣I的距離，所以PI越小，算法的分離性能越好；當(dāng)PI等于“0”時，表示混合信號完全分離。同時，當(dāng)相關(guān)系數(shù)ρ等于“1”時，說明這兩個信號完全分離；當(dāng)ρ趨近于“0”時，說明兩個信號不相關(guān)。實際操作中，從多次的仿真實驗結(jié)果中總結(jié)出經(jīng)驗，當(dāng)ρ大于0.5時，即可認(rèn)為成功分離。

3 去噪分析數(shù)值實驗

3.1 單道探地雷達信號去噪分析

實際測量中，噪聲的類型是多種多樣的，除開地層中不同介質(zhì)產(chǎn)生的背景干擾噪聲，還有儀器本底噪聲，直流漂移的干擾和各種外部因素干擾[15]。為了更貼近生產(chǎn)實際，先加入高斯白噪聲測試去噪效果，然后將高斯白噪聲作為背景噪聲，再加入階躍噪聲和脈沖噪聲測試去噪效果。首先利用探地雷達正演模擬程序得到一道原始數(shù)據(jù)，與附加噪聲通過隨機矩陣進行混合，完成對信號的加噪。在加上噪聲的信號圖中(圖3(b)、圖4(b)、圖5(b)、圖6(b))可見，有效信號特征已經(jīng)基本完全淹沒在噪聲信號中，同時由于是采用隨機矩陣混合的方式，分配加權(quán)系數(shù)的影響使得混合后，信號整體幅值比原始信號小。

從圖3(c)、圖4(c)、圖5(c)、圖6(c)可以看出，淹沒在噪聲中的信號通過FastICA算法進行處理后，很好地恢復(fù)了源信號，達到了去噪的目的，體現(xiàn)了算法的有效性。相比傅立葉變換、S變換、小波變換等算法，F(xiàn)astICA算法在具體實現(xiàn)方面操作起來更為簡單，適應(yīng)性更強。從圖3(c)、圖4(c)、圖5(c)、圖6(c)中還可以發(fā)現(xiàn)，分離后的信號幅值和源信號相比總體放大了近兩倍，變化較大。在計算過程中發(fā)現(xiàn)，分離后的各信號之間順序有時也會發(fā)生變化。這正是盲源分離理論上存在的幅度不確定性和分離順序不確定性問題[16-17]。但是只要存在于信號波形中的信號主要特征沒有發(fā)生改變，上述信號部分特征的變化對算法在地球物理工程實際應(yīng)用中無影響。

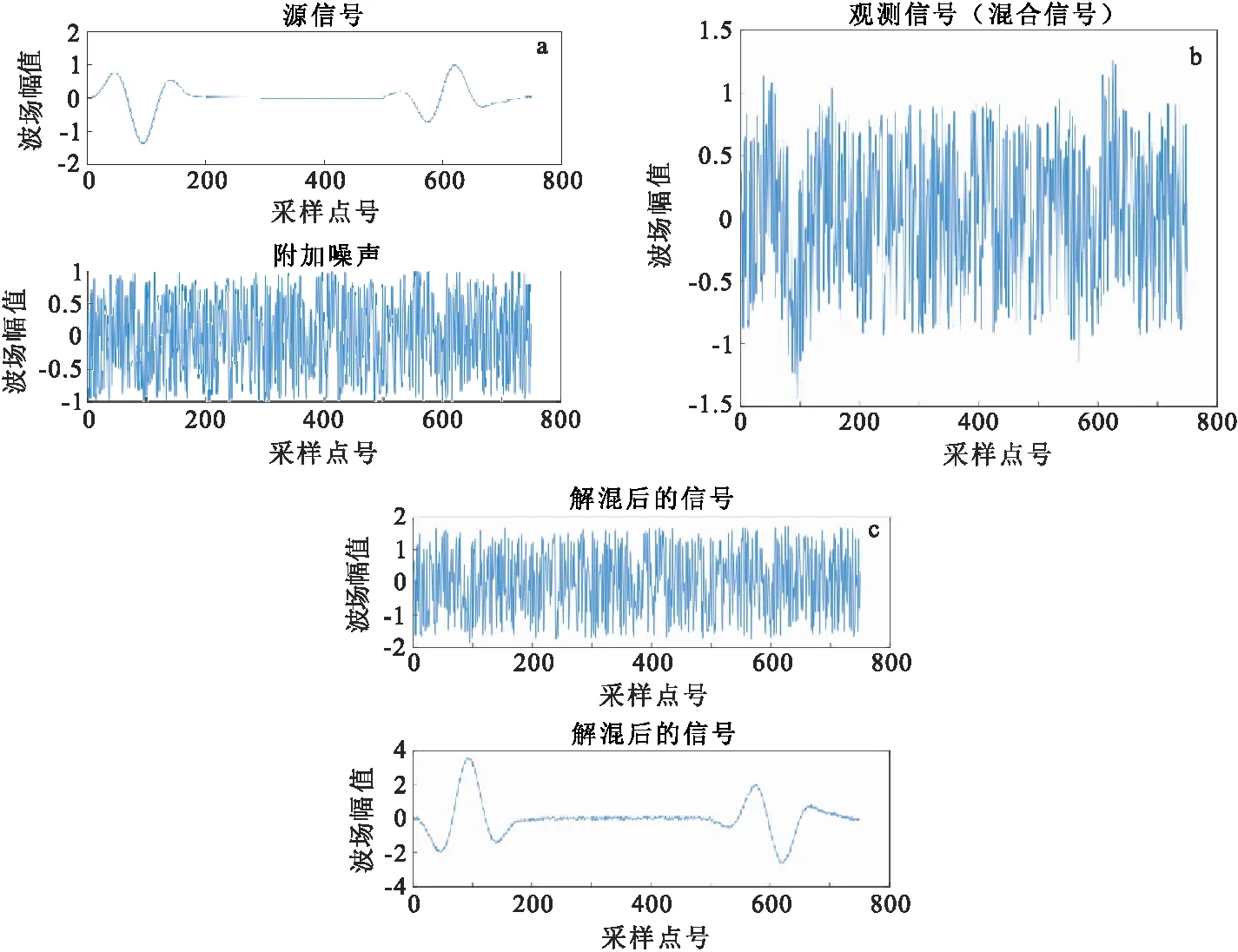
圖3 混合高斯白噪聲Fig.3 Mixed by Gauss white noise(a)源信號；(b)含噪信號；(c)分離結(jié)果

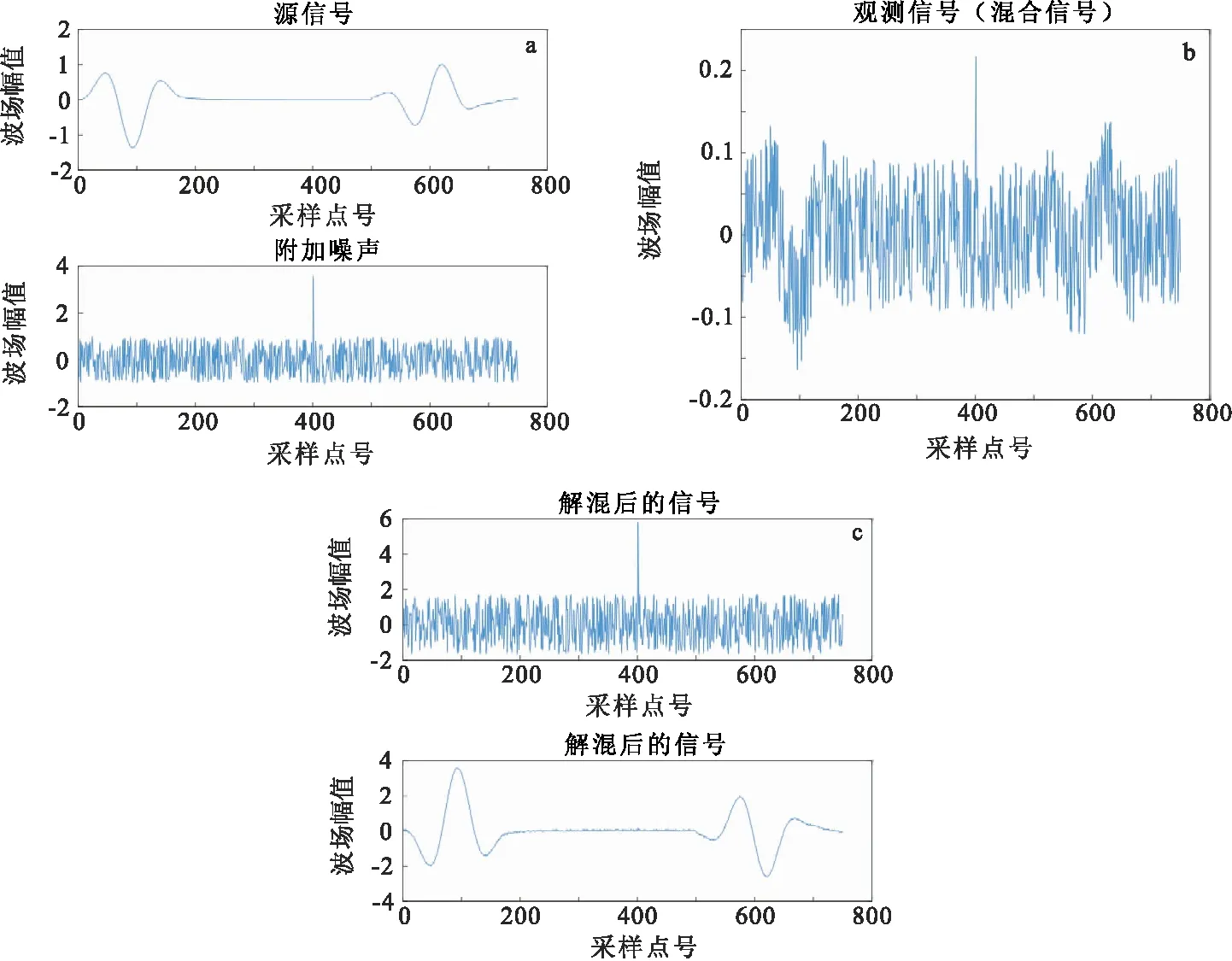
圖4 混合高斯白噪聲和脈沖噪聲Fig.4 Mixed by Gauss white noise and impulse noise(a)源信號；(b)含噪信號；(c)分離結(jié)果

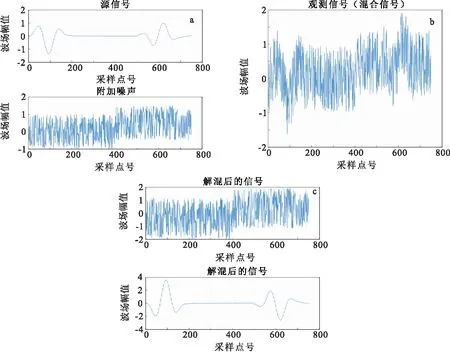
圖5 混合高斯白噪聲和階躍噪聲Fig.5 Mixed by Gauss white noise and step noise(a)源信號；(b)含噪信號；(c)分離結(jié)果

在背景高斯白噪聲中分別加入階躍噪聲和脈沖噪聲作為附加噪聲測試去噪效果。同時，考慮到實際采集中多類噪聲信號并存的復(fù)雜條件，嘗試在背景高斯白噪聲中同時加入階躍噪聲和脈沖噪聲作為附加噪聲測試去噪效果。利用上述的原始數(shù)據(jù)，與附加噪聲通過隨機矩陣進行混合，完成對信號的加噪。在加上噪聲的信號圖中(圖3～圖6)，可見有效信號特征已經(jīng)基本淹沒在噪聲信號中。

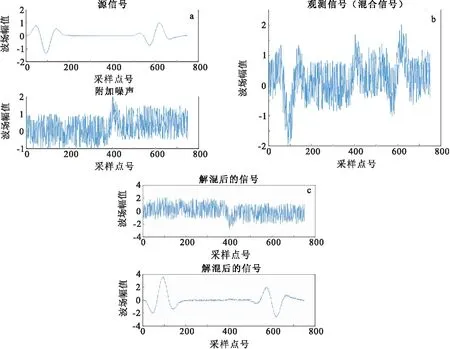
圖6 在背景高斯噪聲中加入階躍噪聲和脈沖噪聲Fig.6 Mixed by Gauss white noise ,step noise and impulse noise(a)源信號；(b)含噪信號；(c)分離結(jié)果

從得到的分離結(jié)果中可以看到，在高斯白噪聲中混合脈沖噪聲或者階躍噪聲兩種條件下，分離結(jié)果和原始數(shù)據(jù)相比，除開幅值整體放大了外，分離的效果都很好，并且在背景噪聲中同時存在階躍噪聲和脈沖噪聲時，算法依然有很好的穩(wěn)健性，去噪效果明顯。表1給出了對于不同附加噪聲條件下FastICA算法分離的性能參數(shù)PI和相關(guān)系數(shù)ρ。表2給出了不同信噪比條件下FastICA算法去噪結(jié)果。從表2中可以看出，F(xiàn)astICA算法對于不同信噪比信號去噪有較強的適應(yīng)性和穩(wěn)定性。

表1 不同附加噪聲條件下FastICA算法分離的性能參數(shù)

表2 不同信噪比條件下FastICA算法去噪結(jié)果

3.2 含噪剖面數(shù)據(jù)的FastICA算法去噪分析

在背景條件復(fù)雜的工區(qū)，現(xiàn)場往往會給探地雷達數(shù)據(jù)采集帶來很多噪聲干擾，如鋼筋網(wǎng)、復(fù)雜的地質(zhì)條件等。因此，為了消除這些噪聲干擾，提高資料解釋的準(zhǔn)確性和可靠性，對信號進行處理，這對復(fù)雜情況下的探地雷達資料處理和解釋是有必要的。

設(shè)計探地雷達應(yīng)用幾何模型，模型寬為0.5 m，深為0.5 m，空間步長為0.005 m。在坐標(biāo)(60，70)處有一半徑為0.02 m的圓形物體，利用探地雷達正演程序進行數(shù)值模擬，天線發(fā)射頻率為900 MHz(圖7)。在圖8中可以看到，加入強噪聲后的剖面圖上，小球的初至波和直達波已經(jīng)基本完全淹沒在噪聲信號中，如果不做任何處理，此時很難分辨出有效信號。

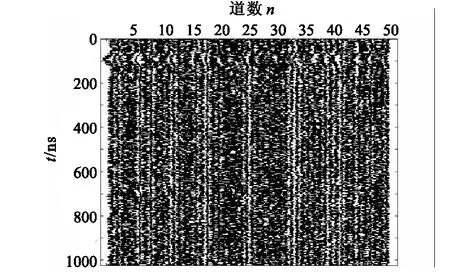
圖7 含噪探地雷達正演合成剖面圖Fig.7 GPR forward simulation section of addition noise

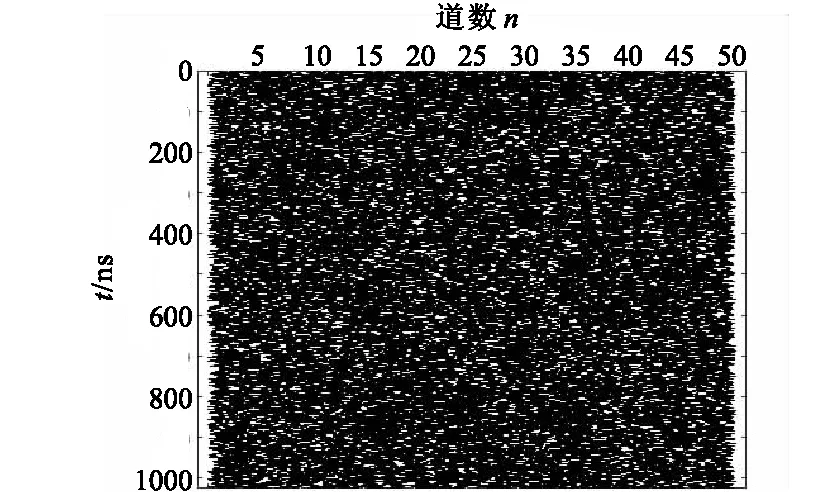
圖8 解混后的噪聲剖面圖Fig.8 Noise section

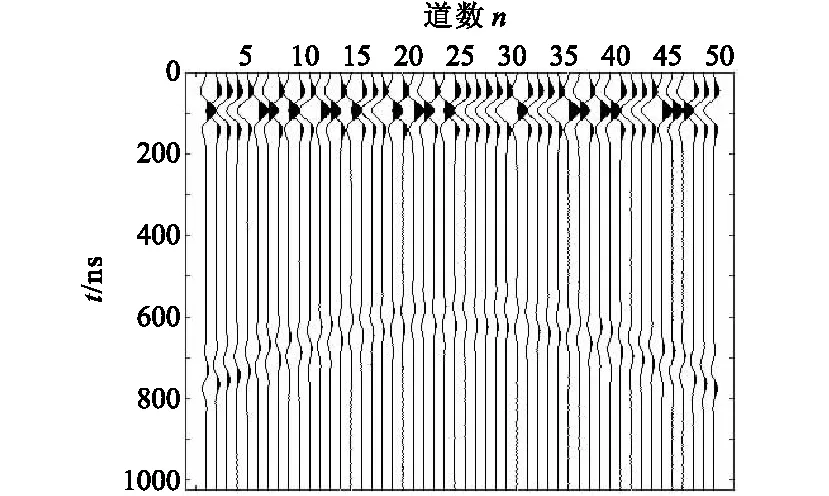
圖9 解混后的初至波剖面圖Fig.9 First arrival section

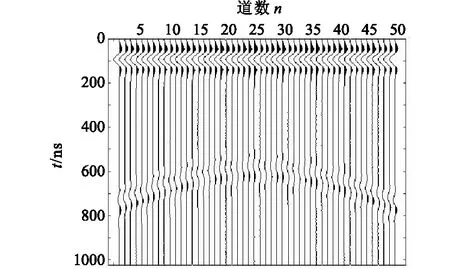
圖10 進行二次處理后的初至波剖面圖Fig.10 First arrival section after post-processes

利用FastICA算法對圖8中的50道數(shù)據(jù)進行去噪處理，得到噪聲剖面(圖8)和初至波剖面(圖9)。從圖9中看到，經(jīng)過FastICA算法處理后，初至波已經(jīng)基本和噪聲分開，研究結(jié)果表明，用FastICA算法去除探地雷達信號中的噪聲是有效的，但是，圖9中第5、7、12、18、19道等數(shù)據(jù)上出現(xiàn)了異常的地方，經(jīng)分析后認(rèn)為這并不是殘余噪聲的影響，而是因為FastICA算法是基于盲源分離理論的，這些異常恰好反映了盲源分離理論有待深入研究的問題之一，即分離后信號可能會發(fā)生反相的現(xiàn)象，這個問題本質(zhì)上和幅度不確定性一樣，都是由矩陣的本質(zhì)相等問題引起[18]，但這對FastICA算法在實際地應(yīng)用中并無較大地影響，可以通過有效手段將其去除。圖10為進行簡單二次處理后的初至波剖面，有效信號的初至更加明顯，圖像分辨率相比第一次解混后(圖9)有了較大地提高，數(shù)據(jù)的信噪比與未處理之前得到了極大地改善，方法的優(yōu)勢顯而易見，并進一步證實了算法的有效性和合理性。

圖11是對含噪剖面數(shù)據(jù)采用傅里葉變換去噪和采用db4基、haar基、sym8基的小波強制去噪效果對比圖。可以看出，相比傅里葉變換和小波變換，在背景噪聲較強的情況下，F(xiàn)astICA算法具有較好的去噪效果。

4 分析實測GPR數(shù)據(jù)

圖12為在湖北恩施土家族苗族自治州彭家寨隧道出口采用探地雷達得到的實測數(shù)據(jù)剖面圖，檢測過程中采用美國GSSI公司生產(chǎn)的SIR-3000型探地雷達儀進行檢測，按照探測目的及要求，選用900 MHz天線，掃描采樣點數(shù)設(shè)為512。從圖12中可以模糊看到存在空洞結(jié)構(gòu)異常，但由于工區(qū)地質(zhì)條件復(fù)雜，巖體破碎，縫隙中有褐黃色物質(zhì)填充，巖性不均，對剖面結(jié)果產(chǎn)生了強烈的干擾，導(dǎo)致異常體形態(tài)模糊，不能準(zhǔn)確定位和判斷解釋。針對該段采用FastICA算法，對實測數(shù)據(jù)進行去噪處理(圖13)。由此可見，經(jīng)過FastICA算法處理的探地雷達剖面圖異常清晰、分辨率高，結(jié)合該段的地質(zhì)條件根據(jù)經(jīng)驗推測此異常為空洞，后經(jīng)鉆探結(jié)果驗證了推測的正確性。

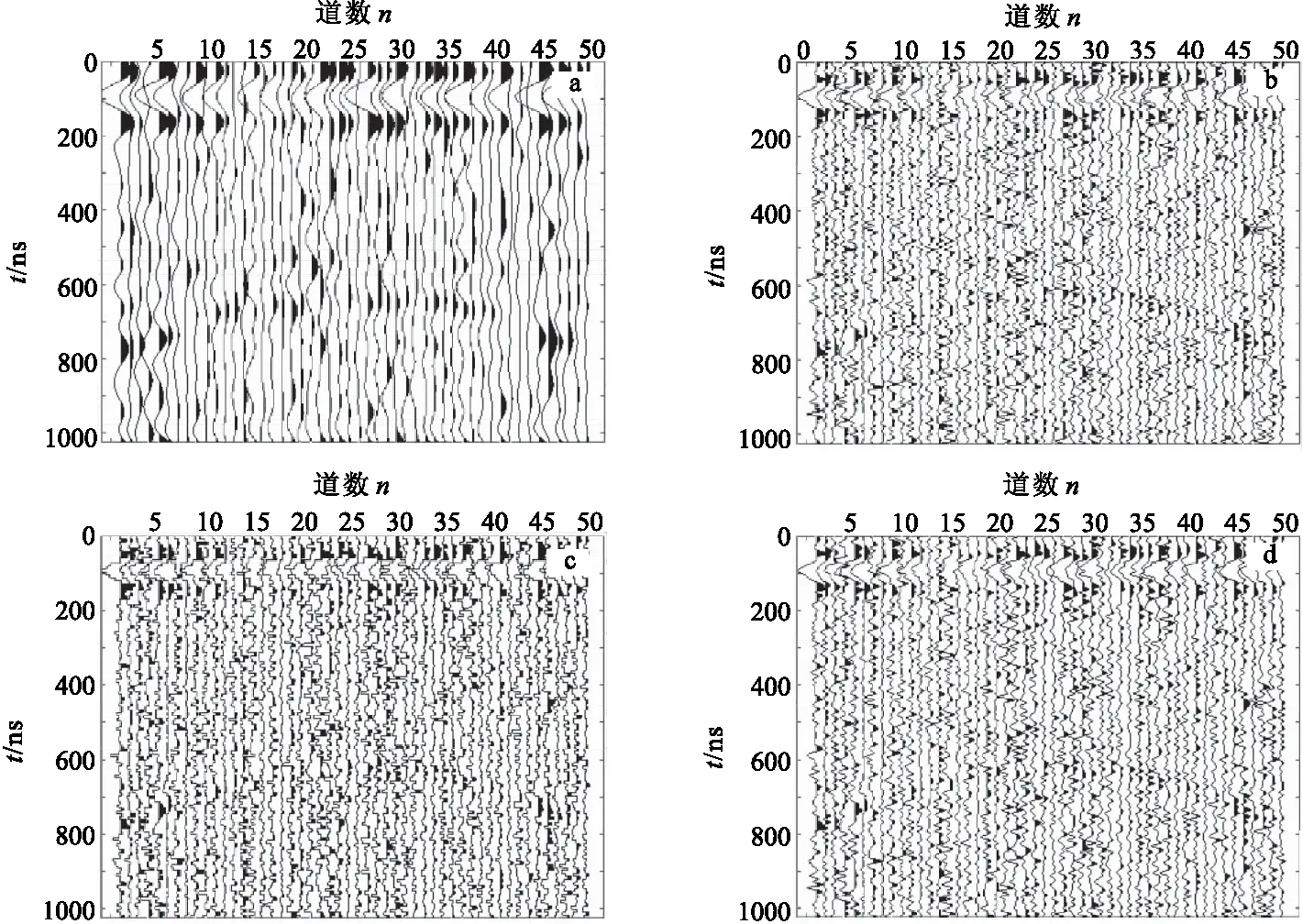
圖11 采用傅里葉變換和小波變換去噪結(jié)果圖Fig.11 Denoising results by using Fourier transform and wavelet transform(a)傅里葉變換；(b)db4基小波強制去噪；(c)haar基小波強制去噪;(d)sym8基小波強制去噪

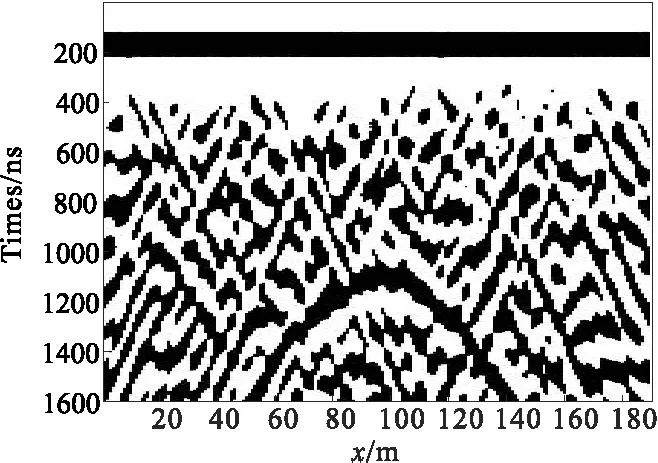
圖12 GPR實測數(shù)據(jù)剖面圖Fig.12 Original section of GPR

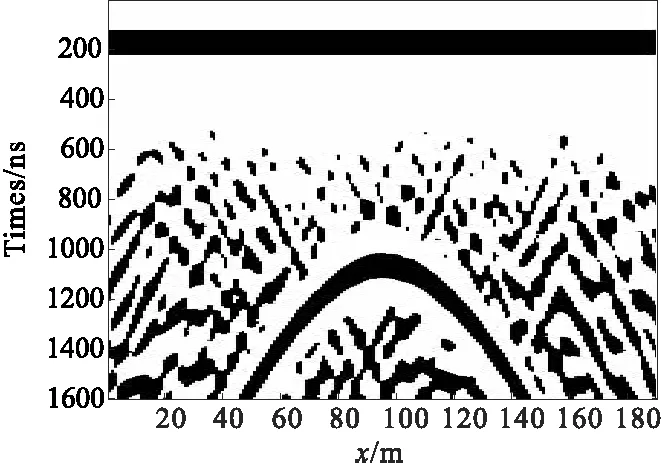
圖13 分離結(jié)果圖Fig.13 The processed result

5 結(jié)論

筆者主要研究了快速獨立分量分析算法在探地雷達信號去噪中地應(yīng)用，對獨立分量分析基本理論和FastICA算法流程進行了介紹，并應(yīng)用FastICA算法進行了探地雷達信號去噪分析。單道信號信噪分離實驗和探地雷達含噪剖面數(shù)據(jù)的處理結(jié)果表明，F(xiàn)astICA算法對探地雷達數(shù)據(jù)中含有高斯白噪聲、脈沖噪聲和階躍噪聲等其他類型的噪聲去除處理，有很好的適應(yīng)性和穩(wěn)健性。將FastICA算法應(yīng)用于探地雷達信號分析不僅算法的參數(shù)設(shè)置簡單方便，而且可以較好地對低信噪比的GPR原始數(shù)據(jù)進行噪聲去除，達到提高數(shù)據(jù)信噪比和資料解釋準(zhǔn)確性的目的，有助于突出探地雷達剖面中異常體特征。證實了快速獨立分量分析算法，應(yīng)用于探地雷達信號去噪的合理性和有效性。

[1] 段煒. 基于小波變換的探地雷達信號去噪方法研究[D].長沙：中南大學(xué),2008.

DUAN W. Research of GPR signal de-noising based on wavelet transform[D].Changsha:Central south University,2008.(In Chinese)

[2] 張麗麗. 探地雷達信號分辨率提高方法研究[D].長春：吉林大學(xué),2012.

ZHANG L L. Research on the method of improving ground penetrating radar signal resolution[D].Changchun:Jilin University,2012.(In Chinese)

[3] 張先武,高云澤,方廣有. 帶有低通濾波的廣義S變換在探地雷達層位識別中的應(yīng)用[J]. 地球物理學(xué)報,2013,01:309-316.

ZHANG X W, GAO Y Z, FANG G Y.Application of generalized S transform with lowpass filtering to layer recognition of ground penetrating radar[J].Chinese Journal Geophysics,2013,56(1): 309-316.(In Chinese)

[4] 鄒海林,隋亞莉,徐俊艷,等. 基于多小波變換的GPR圖象去噪方法研究[J]. 系統(tǒng)仿真學(xué)報,2005(04):855-858+862.

ZOU H L, SUI Y L, XU J Y, at al. Study on methods of GPR image de-noising based on multi-wavelets transform[J]. Journal of System Simulation,2005(04):855-858+862.(In Chinese)

[5] 張志禹,劉亞麗. 基于小波域KL變換的探地雷達信號處理[J]. 煤田地質(zhì)與勘探,2007(02):70-72.

ZHANG Z Y, LIU Y L. Signal processing of ground penetrating radar based on KL transform in wavelet domain[J].Coal Geology&Exploration,2007(02):70-72.(In Chinese)

[6] 王超,沈斐敏. 一維HHT變換在探地雷達數(shù)據(jù)處理中的應(yīng)用[J]. 工程地質(zhì)學(xué)報,2015(02):328-334.

WANG C, SHEN F M.Application of one-dimensional HHT transform to GPR data processing[J].Journal of Engineering Geology,2015(02):328-334.(In Chinese)

[7] 馮德山,戴前偉,余凱. 基于經(jīng)驗?zāi)B(tài)分解的低信噪比探地雷達數(shù)據(jù)處理[J]. 中南大學(xué)學(xué)報(自然科學(xué)版),2012(02):596-604.

FENG D S, DAI Q W, YU K.GPR signal processing under low SNR based on empirical mode decomposition[J].Journal of Central South University (Science and Technology),2012(02):596-604.(In Chinese)

[8] 江華根,楊斌紅,敖春來,等. 基于快速獨立分量分析的自電測井信號去噪[J]. 水文地質(zhì)工程地質(zhì),2013(01):29-33.

JIANG H G, YANG B H, AO C L, et al.Noise removal from spontaneous potential logging signal based on Fastica[J].Hydrogeology&Engineering Geology,2013(01):29-33.(In Chinese)

[9] C.JUTTEN,J.HERAULT. Blind separation of sources.Part I:An adaptive algorithm based on neuro mimetic architecture[J].Signal Processing,1991,24(P):1-10.

[10] 李建鋒. 基于盲源分離的地震信號處理方法研究及應(yīng)用[D].青島：中國石油大學(xué)(華東),2012.

LI J F. Research and application on the method of seismic signal Processing based on blind source separation[D].Qingdao:China University of Petroleum(EastChina),2012.(In Chinese)

[11] 劉喜武,劉洪,鄭天愉. 用獨立分量分析方法實現(xiàn)地震轉(zhuǎn)換波與多次反射波分離[J]. 防災(zāi)減災(zāi)工程學(xué)報,2003(01):11-19.

LIU X W, LIU H, ZHENG T Y. Separation of coverted-wave from seismic multiples by independent component analysis[J].Journal of Disaster Prevention and Mitigation Engineering,2003(01):11-19.(In Chinese)

[12] A.HYVARINEN. E.Oja. Independent component analysis: Algorithm and application[J]. Neural Network,2000,13(4):411-430.

[13] 劉喜武,劉洪,李幼銘. 快速獨立分量變換與去噪初探[J]. 中國科學(xué)院研究生院學(xué)報,2003(04):488-492.

LIU X W,LIU H,LI Y M. Independent component transformation and its testing application on seismic noise elimination[J].Journal of the Graduate School of the Chinese Academy of Sciences,2003(04):488-492.(In Chinese)

[14] A.PARASCHIV-IONESCU, C.JUTTEN, K.AMINIAN,et al. Wavelet denoising for highly noisy source separation[J]. IEEE Conferences on Computer Vision and Pattern Recognition, 1991:586-591.

[15] 周奇才,陳秋峰,馮雙昌. 探地雷達圖像數(shù)據(jù)處理及應(yīng)用研究[J].物探化探計算技術(shù),2010,32(06):666-668.

ZHOU Q C,CHEN Q F,FENG S C. Research on image data processing and application of GPR[J].Computing techniques for geophysical and geochemical exploration,2010,32(06):666-668.(In Chinese)

[16] 鄧丹敏. 基于盲信號理論的地震數(shù)據(jù)處理技術(shù)研究[D].長沙：中南大學(xué),2014.

DENG D M .Research on the technology of seismic data processing based on theories of blind signal[D].Changsha:Central south University,2014.(In Chinese)

[17] A.HYVARINEN. Survey on independent component analysis[J]. Neural Computing Surveys,1999,2(P):94-128.

[18] CARDOSO J.F. ,LAHELD B.H. Equivariant adaptive source separation[J]. IEEE Trans. Signal Proceeding,1996,44(12):3017-3029.

Lowsignal-noiseratioGPRsignaldenoisingbasedonFastICA

DAI Qianwei1,2， CHENG Qinyu1， FENG Deshan1,2

(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China；2. Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Ministry of Education,Central South University, Changsha 410083, China)

To improve the accuracy and reliability of interpretation of ground penetrating radar (GPR) prospecting data in complex area, independent component analysis (ICA) is used for GPR data de-noising process in strong background noise. In this work, the basis theory for ICA is firstly introduced, and negative entropy-based FastICA algorithm is discussed in details. In the following discussion, applied to the de-noising process of single channel GPR data and forward modeling cross-sectional data with noise. Besides, the GPR data from Hubei Enshi transit tunnel is collected for the further test of this FastICA algorithm in this paper. The results show that FastICA algorithm overcomes the constraints on parameter set in traditional methods for GPR data process, simply process, and has advantage on GPR data de-noising, especially for low signal-noise GRP data. The de-noising data can highlight the characteristics of anomalies, which is helpful for improving the accuracy and reliability of interpretation.

independent component analysis; GPR; negative entropy-based; Fast ICA; de-noising

2016-09-05 改回日期： 2016-09-29

國家自然科學(xué)基金資助項目(41374118)

戴前偉(1968-)，男，博士，教授，主要從事電法、探地雷達和重磁的數(shù)值模擬及理論研究，E-mail：qwdai@csu.edu.cn。

成沁宇(1992-)，男，碩士，從事探地雷達信號處理，E-mail：qinyucheng@csu.edu.cn。

1001-1749(2017)06-0727-09

P 631.4

A

10.3969/j.issn.1001-1749.2017.06.03