基于匹配追蹤時頻譜計算的砂體尖滅線檢測方法

汪瑞良， 張文珠， 劉徐敏， 董國輝， 李志曄

(中海石油(中國)有限公司 深圳分公司，深圳 518000)

基于匹配追蹤時頻譜計算的砂體尖滅線檢測方法

汪瑞良， 張文珠， 劉徐敏， 董國輝， 李志曄

(中海石油(中國)有限公司 深圳分公司，深圳 518000)

匹配追蹤算法能夠實現信號的自適應分解。首先研究了快速動態匹配追蹤算法，實現了匹配追蹤高分辨率時頻譜計算，然后通過構建楔形砂體模型深入剖析了薄砂儲層的時域和頻域反射特征，發展了利用時頻譜分量來指示砂體尖滅點位置的方法。該方法綜合了薄層調諧能量和薄層反射向高頻移動的特征，采用相對高頻的瞬時譜分量的異常高值識別薄砂尖滅點，相比單獨使用振幅屬性的尖滅點檢測方法精度有所提高。模型試算驗證了利用時頻譜分量來指示砂體尖滅點位置的方法識別薄層砂體尖滅點的有效性,在實際資料的薄砂尖滅識別應用中，該方法取得了較好的效果，有效地證實了其實用性和可靠性。

匹配追蹤； 尖滅線檢測； 薄層砂體； 時頻分析

0 引言

隨著勘探形勢的日益復雜，復雜巖性圈閉邊界的精確落實以及砂泥巖尖滅線檢測已經成為國內、外研究難點。由于地震信號在地下復雜介質傳播過程中受到大地濾波作用，地震信號是一個帶限信號，地震資料的垂直分辨率較低。當儲層厚度小于調諧厚度(約1/4波長)時，干涉作用導致相鄰地層界面的有效反射形成單個復合波，因此，時間域振幅信息難以準確有效地識別薄砂儲層的空間尖滅位置。

為了克服地震資料分辨率的局限性，高分辨率地震采集和處理方法被不斷提出并得到了廣泛應用(寬頻地震采集、時頻譜白化、吸收衰減補償(Gabor反褶積)以及稀疏反褶積等)，這為利用地震資料識別薄層提供了較好的數據基礎[1-6]。基于地震屬性的薄層分析方法在地震解釋領域發展迅速，其主要包括振幅類、頻率類、相位類、相干類以及幾何類等屬性。作為一種數據驅動的解釋手段，地震屬性薄層分析需明確屬性與薄層結構之間的映射關系[7]。李國發等[8]研究了基于模型的薄互層振幅屬性分析及應用，總結出了薄互層砂體累計厚度和反射振幅之間的定量關系。薄層調諧能量對應的位置十分接近真正的尖滅點，且此位置在瞬時譜剖面會形成亮點，容易被識別和追蹤，因此可利用瞬時譜特征指示尖滅位置。

地震信號本質上是一種非平穩信號，即信號所含的頻率分量隨著時間的變化而變化，地層厚度變化和吸收衰減效應等都會引起頻率異常現象。針對非平穩地震信號的時頻分析方法主要包括短時傅立葉變換(STFT)、連續小波變換(CWT)、S變換(ST)以及Wigner-Ville分布等，這些常規的時頻分析方法雖然計算效率高，但不能滿足識別砂體尖滅線的精度要求。相比傳統的時頻分析方法，基于匹配追蹤的時頻分析能夠較好地適應信號本質結構特征，對地層的識別能力更強，可用于對薄砂巖儲層尖滅的識別[9-12]。何胡軍等[13]通過基于匹配追蹤算法的子波分解技術識別薄互層儲層；相比張繁昌等[14]研究的基于匹配追蹤瞬時譜計算的于三角洲砂體尖滅線識別，筆者結合實際地質沉積模式構建地層薄砂互層模型，對復雜沉積模式下的尖滅線識別進行了更全面地研究分析。

筆者在前人研究的基礎上，首先研究了基于Morlet小波的快速匹配追蹤算法，并通過理論信號和地震信號，驗證了幾種常規時頻分析方法和匹配追蹤時頻譜計算結果的時頻分辨率特征差異。其次，通過構建楔形模型和薄砂互層模型研究了薄層砂體的振幅和頻率響應特征，分析發現薄層調諧振幅位置已十分接近真正砂體尖滅點；在此基礎上，綜合薄層反射位置的頻率域響應信息，利用時頻譜分量來指示砂體尖滅點位置，相比單獨使用振幅屬性的尖滅點檢測精度有所提高。最后，通過對某海域實際資料砂體沉積尖滅線的檢測，驗證利用時頻譜分量來指示砂體尖滅點位置的方法的有效性。

1 砂體尖滅線識別原理

1.1 匹配追蹤時頻分析

時頻分析方法主要可分為三大類：①窗口限制的線性時頻表征方法；②非線性時頻分布方法；③反演譜分解。第一類線性時頻表征的分辨率主要取決于窗口長度的選擇， STFT僅具有單一的時頻分辨特征，而CWT、ST等在實現過程中具有自適應的分辨能力；第二類非線性時頻分布由于不涉及時間窗口的選擇，因此不存在分辨率的問題，如Wigner-Ville分布(WVD)具有較高的時頻分辨率，但其存在交叉項干擾的問題。匹配追蹤算法(MP)可實現信號的自適應分解，通過將信號在超完備時頻原子庫中進行投影，將地震信號表示為匹配原子的線性組合形式。

時頻原子庫是一系列時頻原子的集合，也稱為字典，常用的時頻原子是對窗函數g(t)進行拉伸、平移與調制得到。由高斯窗函數產生的時頻原子具有最高的聯合時頻分辨率，Morlet小波作為一種高斯窗函數調制的時頻原子被廣泛應用于地震勘探中，Morlet小波字典具體表達式如式(1)所示。

D={mγ(t)}γ∈Γ={mγ=(u,ω,φ)(t)}γ∈Γ

(1)

式中：γ=(u,ω,φ)為時頻原子的調制參數；u為中心時間延遲；ω為調制頻率；φ為調制相位。字典D中的原子是非正交的且是過完備的，信號f在D中的分解是稀疏的，其分解可以等價為式(2)所示的優化問題，通過控制迭代次數δ和迭代閾值ε實現信號的自適應投影分解。

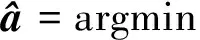
(2)

式中：a為稀疏表示系數向量;f為原始地震信號向量。

匹配追蹤算法是一種貪婪迭代算法，能夠很好地對式(2)進行求解，即估計信號f在字典D中原子上的投影。首次迭代后信號f可以被分解為沿mγ1方向及垂直方向分量之和：

f=[f,mγ1]mγ1+R1f

(3)

式中：[f,mγ1]為信號f與原子mγ1的內積，即信號f沿mγ1方向的分量；R1f為投影近似后的殘差信號，即信號f沿與mγ1垂直方向的分量。為使殘差信號盡可能小，選擇最佳原子應滿足式(4)。

|[f,mγ1]|=max{|[f,mγn|,n=1，2，L}

(4)

利用同樣的方法繼續對殘差進行分解，假設迭代算法已經進行了N次，得到殘差信號為RNf，信號f可以分解為：

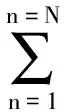
(5)

式中：mγn(u,ω,φ)為時頻匹配原子；an為時頻原子的振幅系數。

針對匹配追蹤算法巨大計算量的問題，考慮原始信號的瞬時振幅、瞬時頻率和瞬時相位等先驗信息[14]，進一步約束頻率和相位的搜索半徑，從而提高匹配追蹤的計算效率。因此每一次搜索方式可以簡單表述為式(6)。

γn={u0,ω∈U[ω(u0),δω],φ∈U[φ(u0),δφ]}

(6)

式中：u0={t0:A(t0)=max[A(t)]}為最大振幅包絡對應的時間；A(t)、φ(t)和ω(t)分別表示地震信號的瞬時振幅、瞬時相位及瞬時頻率信息；U[ω(u0),δω]、U[φ(u0),δφ]為頻率和相位搜索鄰域；δω、δφ為相應參數搜索半徑。按照上述快速匹配追蹤原理即可實現地震信號的自適應分解，借助Wigner-Ville分布的高時頻分辨率特征，則其時頻能量譜可以表示為匹配原子WVD分布的疊加形式

(7)

時頻譜Wf(t,ω)不但繼承了WVD分布的高分辨率特征，而且消除了WVD分布存在的交叉項干擾的問題。

我們設計了由10個Morlet小波組成的理論信號，針對匹配追蹤算法的稀疏重構能力進行了測試，圖1中黑色曲線Syn為理論信號，紅線Rec為匹配重構信號，Res為匹配殘差信號，1st-10th分別表示逐次迭代原子的結果。由此可見，匹配重構信號與理論信號基本保持一致，可較好地識別出合成信號中不同頻率、不同相位的Morlet小波原子。

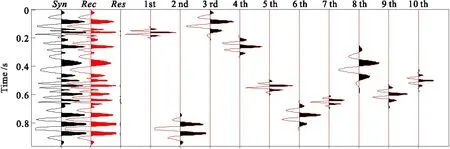
圖1 理論信號匹配追蹤信號重構過程Fig.1 Reconstruction process of theoretic signal matching pursuit

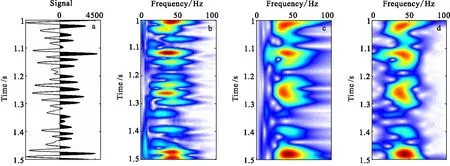
圖2 地震信號時頻分析分辨率特征對比Fig.2 Characteristics comparison of different spectrum analysis methods(a)信號；(b)MP；(c)CWT；(d)STFT

為了驗證基于Morlet小波的動態匹配追蹤WVD時頻表征方法的應用效果，通過對1D地震信號MP時頻譜與連續小波變換(CWT)及短時傅立葉變換(STFT)的時頻譜對比分析，由圖2可以看出，MP時頻譜的時間和頻率分辨率均要高于常規時頻分析方法。MP高分辨率時頻譜分解方法為薄層砂巖尖滅點識別奠定了數據基礎，有助于提高砂泥巖尖滅線的識別精度。

1.2 砂體尖滅線識別原理

為了研究薄層反射信號的振幅和頻率響應特征，我們采用25 Hz的雷克子波對楔形地層模型進行了正演(圖3、圖4)。

由圖4(a)和圖4(b)可見，單楔體情況下，反射最大振幅(均方根振幅)，隨砂體厚度的增大呈現先增大后減小最后達到穩定的變化特征，瞬時頻率則呈現先減小后增大最后趨于穩定的變化特征。此外，當薄層厚度小于調諧厚度時(圖4中黑線和紅線指示位置，砂體厚度為子波波長的1/4)，最大振幅與薄層厚度呈正相關關系，瞬時頻率與薄層厚度呈負相關關系。

由圖4(c)和圖4(d)可見，薄互層的振幅和頻率隨砂體總厚度的變化趨勢與單楔形模型基本一致。由于地震資料受到“子波疊印”的影響[15]，僅僅利用地震振幅信息難以識別出可靠的砂巖尖滅位置；瞬時頻率和瞬時相位屬性在實際地震資料中不穩定存在[16]，因此均難以提供較為準確和可靠的砂巖尖滅點識別效果。結合上述，要綜合薄層位置的反射振幅和頻率信息發展時頻域砂體尖滅線識別方法，利用時頻譜分量來指示砂體尖滅點位置。時頻域地震信號比振幅屬性的尖滅點檢測精度要高，它克服了單獨使用瞬時頻率信息進行尖滅點識別的不穩定問題。

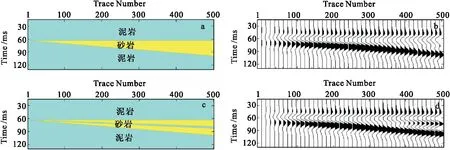
圖3 楔形體模型及合成地震記錄Fig.3 Wedge models and corresponding synthetics(a)單楔形理論模型；(b)單楔形合成地震；(c)雙楔形理論模型；(d)雙楔形合成記錄

圖4 楔形體最大振幅和瞬時頻率響應分析Fig.4 Maximum amplitude and instantaneous frequency analysis of wedge models(a)單楔形最大振幅；(b)單楔形瞬時頻率；(c)雙楔形最大振幅；(d)雙楔形瞬時頻率

基于地震振幅的薄層尖滅點識別方法，僅能夠識別至調諧能量位置處，而基于時頻譜的尖滅線識別方法，綜合利用了調諧尺度內頻率隨地層厚度減小而增大的信息，時頻譜中薄層反射信號的能量團向高頻端移動(調諧尺度內)，通過選取高頻瞬時譜分量即可提高尖滅點的識別精度。由于地震頻帶寬度是局限的，不存在無限增大的現象，因此地震頻帶寬度越寬，薄層尖滅點的識別精確越高。同時，借助高分辨率匹配追蹤時頻分析方法計算地震信號時頻譜，為薄層尖滅點的精確識別提供了可靠的數據基礎。

2 模型試算

為了驗證基于時頻譜分析的砂體尖滅線識別方法的可行性與穩定性，根據我國某南部探區中的地質沉積模式構建了2套縱波阻抗地層尖滅模型。模型頂部為泥巖地層，泥巖地層下方包含兩套薄砂互層，泥巖和薄砂互層之間發育一套高阻地層(圖5和圖6)。模型大小為橫向上CDP道數為450，縱向上采樣時長為300 ms，采樣間隔為1 ms，上覆砂體尖滅位置在CDP100位置。

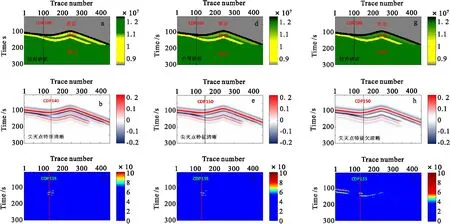
圖6 不同巖性充填縱波阻抗模型以及砂體尖滅點檢測結果Fig.6 Impedance models filled with different lithology and corresponding pinch-out point detection results(a)理論地質模型IV；(b)模型IV合成地震記錄；(c)模型IV去強反射道集；(d)理論地質模型V ；(e)模型V合成地震記錄；(f)模型V去強反射道集；(g)理論地質模型VI；(h)模型VI合成地震記錄；(i)模型VI去強反射道集

圖5(a)、圖5(d)、圖5(g)為不同厚度泥巖隔層縱波阻抗模型I、II、III，泥巖隔層厚度依次為3 ms～13 ms、2 ms～8 ms及1 ms～3 ms，砂體厚度變化范圍為1 ms～12 ms，高速層厚度為10 ms～13 ms。利用主頻為25 Hz的零相位Ricker子波基于褶積模型合成地震記錄如圖5(b)、圖5(e)、圖5(h)所示，由圖5(b)、圖5(e)、圖5(h)中可見，砂巖尖滅點位置受到地震波不同程度的模糊作用，僅依靠地震剖面中的相位突變點難以精確識別砂巖尖滅位置。此外，隨著泥巖隔層厚度的不斷減小，尖滅點的識別精度不斷下降(相位突變點：CDP145- CDP150- CDP165)。圖5(c)、圖5(f)、圖5(i)為基于時頻譜分析的尖滅點識別結果，分析圖5(c)、圖5(f)、圖5(i)可得，由于時頻譜分析綜合了薄層的振幅和頻率響應信息，尖滅點識別位置相比相位突變點更加可靠，并且精度更高(能量異常點：CDP130- CDP143- CDP155)，相比振幅相位突變點檢測到的尖滅點位置向前逼近了約10-15個采用點。

圖6(a)、圖6(d)、圖6(g)為不同巖性充填縱波阻抗模型IV、V、VI，巖性的充填差異主要體現在砂巖和泥巖的縱波阻抗差異上(砂巖為低阻地層)，模型VI中較差砂質代表砂巖和泥巖的縱波阻抗差較小。圖6(c)、圖6(e)、圖6(h)為對應模型IV、V、VI的合成地震記錄。分析圖6(c)、圖6(e)、圖6(h)發現，地震剖面上“砂體尖滅點”位置依次在CDP140、CDP150、CDP150，與真實尖滅點位置CDP100仍然存在較大的差距。圖6(c)、圖6(f)、圖6(i)為砂體尖滅點的時頻譜檢測結果，由圖6(c)、圖6(f)、圖6(i)可見，匹配追蹤算法可以有效檢測出調諧尺度內比較可靠的尖滅點位置(CDP135、CDP135、CDP135)，并且相比地震剖面中的相位突變點識別精度有所提高。

3 實際資料處理

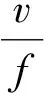
圖7(a)為原始地震剖面I，其中綠色箭頭指示位置為地震剖面中相位突變點；圖7(b)為相位突變處地震道集的時頻譜分析結果，由圖7可見MP-WVD時頻譜的時間和頻率分辨率明顯要高于CWT時頻譜，因此MP-WVD可以更好地為薄層砂體尖滅點識別提供有效的數據基礎。

對比圖8(a)和圖8(b)可得，兩種方法均能有效的識別出尖滅點大致位置；但由于CWT譜時頻分辨能力的局限性，尖滅點在地震剖面中的時空展布仍然存在較大的誤差，而MP-WVD方法識別結果的分辨能力卻有較大程度地提高。

圖9(a)為工區內的另一地震剖面，尖滅點無明顯相位突變現象，圖9(b)為其尖滅點檢測結果，從圖9(b)中可看出，MP時頻譜落實了沉積砂體的尖滅位置(圖9(a)中綠色箭頭所指處)出現了明顯的能量異常現象，該識別效果與地質沉積背景相一致。

針對3D地震資料，開展了各期沉積體邊界平面展布預測。圖10為各期沉積體邊界平面展布范圍預測結果。由于該實際工區多期前積砂體受到砂巖厚度、泥巖隔層厚度、砂巖品質以及砂體連通性等因素的影響，存在多種尖滅點類型，不同尖滅點類型需要優選不同頻率成分進行分析。因此在落實砂體邊界平面展布時，綜合了多個優勢頻率瞬時譜的能量。圖10中所示的3期沉積體邊界預測結果與地質沉積環境相吻合，從而驗證了本文方法的實用性和可靠性。

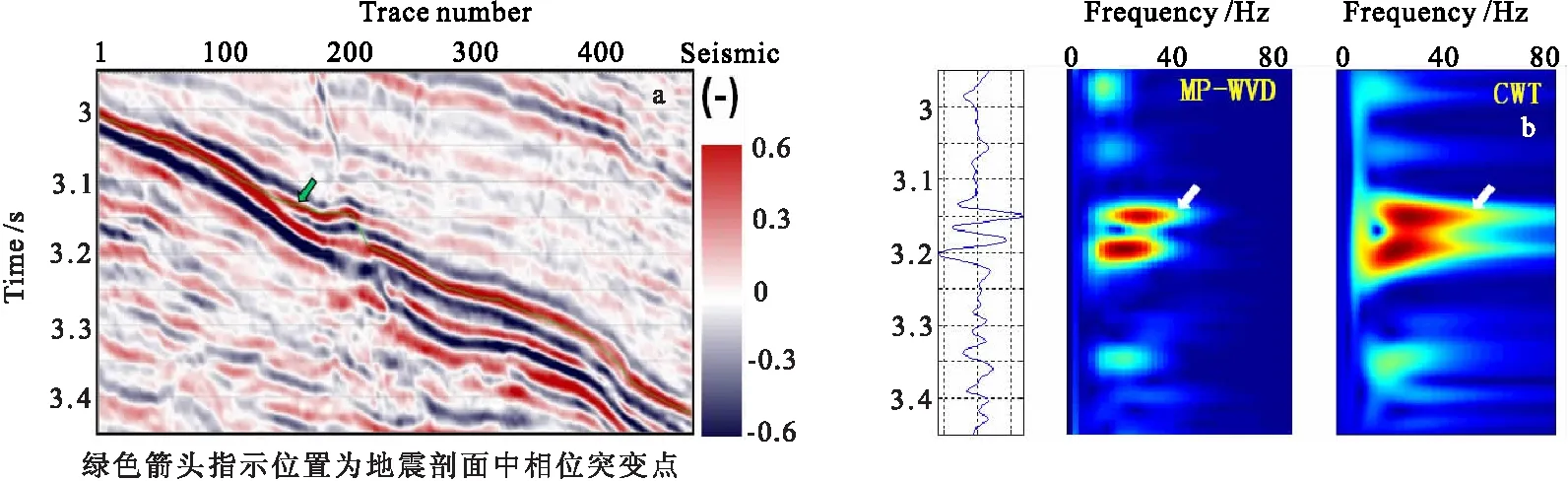
圖7 原始地震剖面I以及尖滅點位置時頻譜分析Fig.7 Orignal seismic section I and spectrum analysis corresponding to pinch-out trace(a)原始地震數據I；(b)尖滅點位置時頻譜

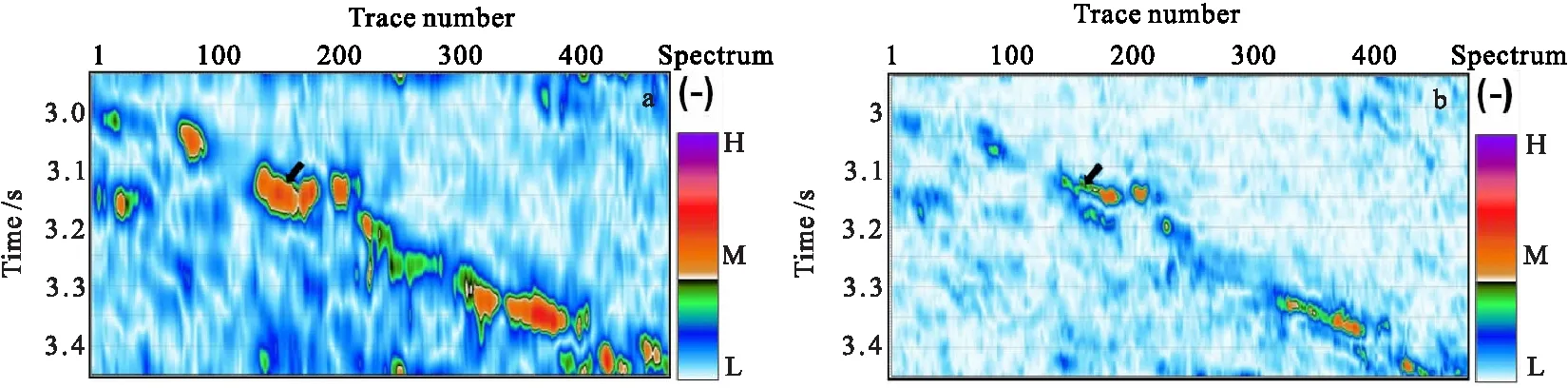
圖8 地震剖面I的CWT譜和MP-WVD譜的尖滅點識別結果Fig.8 Pinch-out detection results of CWT and MP-WVD spectrums corresponding to orignal seismic section I(a)CWT檢測結果；(b)MP檢測結果

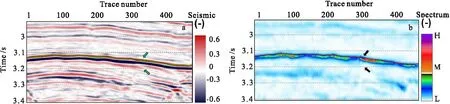
圖9 原始地震數據II及時頻譜檢測結果Fig.9 Orignal seismic section II and spectrum analysis corresponding to pinch-out trace(a)原始地震數據II；(b)MP時頻譜檢測結果

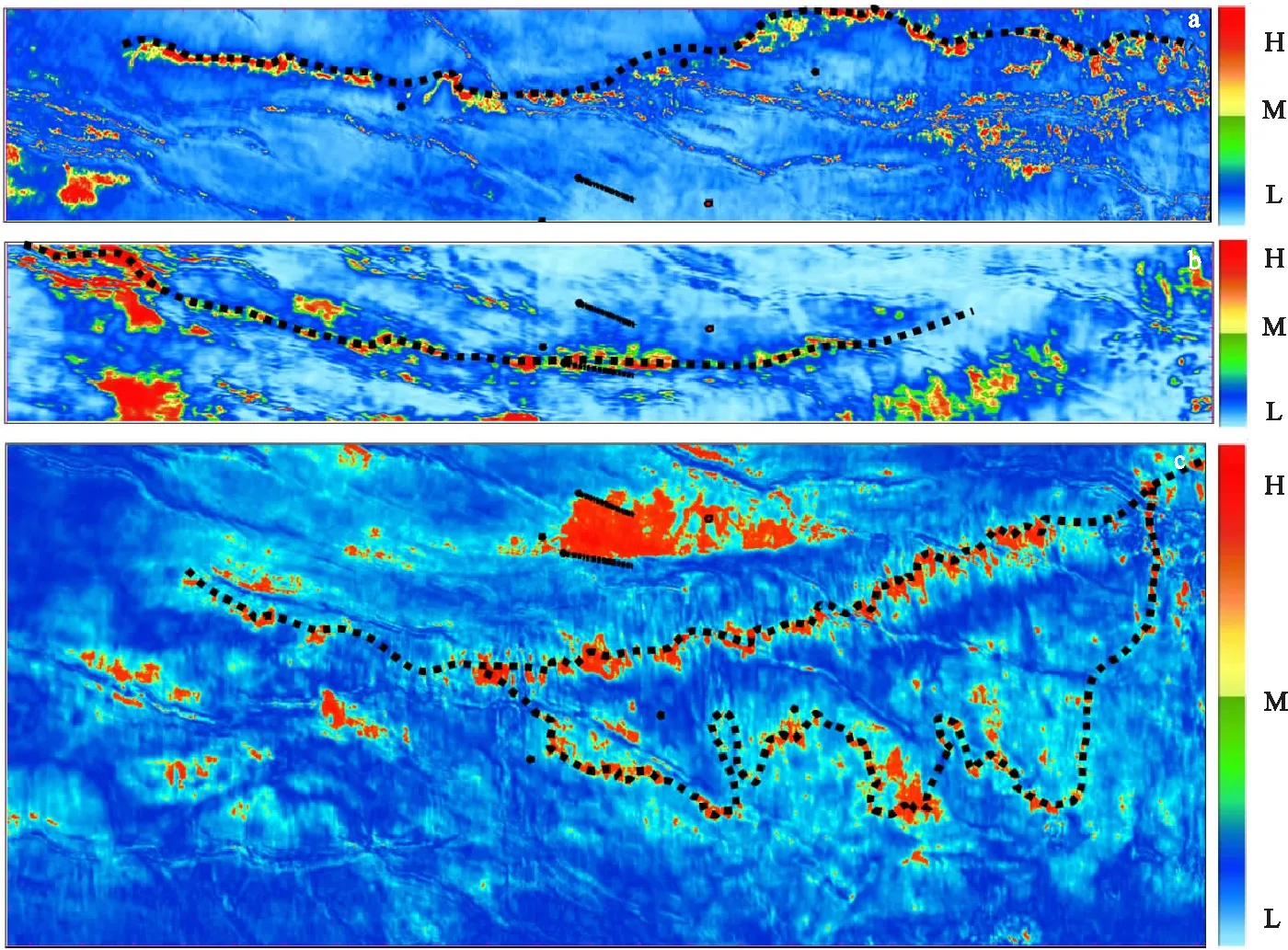
圖10 各期沉積體邊界平面展布范圍預測結果Fig.10 Predicted sediments distribution map in different stages(a)砂體尖滅線I；(b)砂體尖滅線II；(c)砂體尖滅線III

4 結論

通過對比分析了常規時頻分析方法與匹配追蹤時頻譜計算方法的時頻分辨率特征，發現匹配追蹤時頻譜具有最高的時頻分辨率。針對薄層砂體的尖滅線檢測，利用地震資料振幅本身均難以達到理想的識別效果。筆者發展了基于瞬時譜的薄層砂巖尖滅線檢測方法，該方法綜合利用了薄層反射的時間域和頻率域響應信息，利用時頻譜分量來指示砂體尖滅點位置，比振幅屬性的尖滅點檢測方法精度更高；同時，該方法建立在高分辨率時頻譜計算的基礎上，薄層尖滅點的識別精確又有較大的提高。此外，值得關注的是，由于薄層砂體沉積環境的復雜性，薄層砂體邊界的平面預測往往需要綜合優勢頻帶內多頻率瞬時譜分量，才能更好地落實薄層砂體邊界的沉積全貌。

[1] CHAI XINTAO, WANG SHANGXU, YUAN SANYI, et al. Sparse reflectivity inversion for nonstationary seismic data [J]. Geophysics, 2014, 79(3): V93-V105.

[2] NGUYEN T. High resolution seismic reflectivity inversion[D]. Houston: University of Houston, 2008.

[3] ZHANG RUI, CASTAGNA JOHN. Seismic sparse-layer reflectivity inversion using basis pursuit decomposition[J]. Geophysics, 2011, 76(6):147-158.

[4] CHOPRA S., CASTAGNA J. P. , PORTNIAGUINE O. Thin-bed reflectivity inversion[C]. 76th SEG Annual International Meeting, 2006：2057-2061.

[5] 賀錫雷，黃德濟，賀振華. 薄互層反射系數序列時～頻特征研究[J]. 物探化探計算技術，2009，31(3):227-232

HE X L, HUANG D J, HE Z H. Research on time-frequency characteristics of reflection coefficients of thin interbeds[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2009，31(3):227-232.(In Chinese)

[6] 孫雷鳴，曾維輝，方中于. 地震薄層反射系數譜反演算法研究及應用[J]. 物探化探計算技術，2014，36(4):462-470.

SUN L M，ZENG W H,FANG Z Y.Thin-bed reflectivity inversion and seismic application[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2014，36(4):462-470. (In Chinese)

[7] 李國發，岳英，國春香,等. 基于模型的薄互層地震屬性分析及其應用[J]. 石油物探，2011，50(2): 144-149.

LI G F,YUE Y,GUO C X, et al. Seismic attributes analysis based on model in thin interbedded layers and its application[J].Geophysical Prospecting for Petroleum，2011，50(2): 144-149. (In Chinese)

[8] 李國發，岳英，熊金良,等. 基于三維模型的薄互層振幅屬性實驗研究[J]. 石油地球物理勘探，2011，46(1): 115-120.

LI G F,YUE Y,XIONG J L, et al. Experimental study on seismic amplitude attribute of thin interbed based on 3D model[J]. Oil Geophysical Prospecting，2011，46(1): 115-120. (In Chinese)

[9] MARFURT S, ZHANG Z. Matchging-pursuit with time frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12)：3397-3415.

[10] 張繁昌，李傳輝，印興耀. 基于動態匹配子波庫的地震數據快速匹配追蹤[J]. 石油地球物理勘探，2010，45(5):667-673.

ZHANG F C,LI C H , YIN X Y. Seismic data fast matching pursuit based on dynamic matching wavelet library[J].Oil Geophysical Prospecting，2010，45(5):667-673. (In Chinese)

[11] 張繁昌，李傳輝. 地震信號復數域高效匹配追蹤分解[J]. 石油地球物理勘探，2013，48(02):171-175.

ZHANG F C,LI C H.Complex domain efficient matching pursuit decomposition of seismic signals[J]. Geophysical Prospecting for Petroleum, 2013，48(02):171-175. (In Chinese)

[12] 劉杰，張忠濤，劉道理,等. 強反射背景下沉積體邊界檢測及流體識別方法[J]. 石油物探，2016，55(1):142-149.

LIU J Z,ZHANG Z T,LIU D L，et al.Sediment boundary identification and fluid detection for the seismic data with strong background reflections[J]. Geophysical Prospecting for Petroleum,2016，55(1):142-149. (In Chinese)

[13] 何胡軍，王秋語，程會明. 基于匹配追蹤算法子波分解技術在薄互層儲層預測中的應用[J]. 物探化探計算技術，2010，32(6):641-644.

HE H J, WANG Q Y, CHENG M H.The application of wavelet decomposition technique based on matching pursuit algorithm in thin interbedded reservoir prediction[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2010，32(6):641-644. (In Chinese)

[14] 張繁昌，李傳輝，印興耀. 三角洲砂巖尖滅線的地震匹配追蹤瞬時譜識別方法[J]. 石油地球物理勘探，2012，47(1): 82-88.

ZHANG F C,LI C H,YIN X Y.Delta fringe line recognition based on seismic matching pursuit instantaneous spectral characteristics[J].Oil Geophysical Prospecting，2012，47(1): 82-88. (In Chinese)

[15] 劉豪, 辛仁臣.油氣儲層地震綜合預測技術與應用[M].北京：中國地質大學出版社，2013.

LIU H,XIN R C.Seismic integrative prediction of reservoir and hydrocarbon[M].Binjing:China University of Geoscience Press,2013.(In Chinese)

[16] 高靜懷，陳鳳，陳樹民.利用地震瞬時譜屬性進行薄互層分析[J].煤田地質與勘探，2005,33(5)：67-70.

GAO J H,CHEN F,CHEN S M.Using seismic instantaneous attributes to analyze thin interbeds[J]. Coal Geology & Exploration , 2005,33(5)：67-70. (In Chinese)

Themethodofthinsandpinch-outboundarydetectionviaT-Fspectrumbasedonmatchingpursuit

WANG Ruiliang, ZHANG Wenzhu, LIU Xumin, DONG Guohui, LI Zhiye

(CNOOC China LIMITED-Shenzhen, Shenzhen 518000, China)

The adaptive decomposition of seismic signal can be performed by Matching pursuit algorithm. The fast dynamic matching pursuit algorithm is studied, and the computation of high resolution spectrum of seismic data is accomplished in this study. We analyzes the reflection characteristics in time domain and frequency domain through the wedge models-based forwarding, and then develops the method of detection of pinch-out boundary of thin sand reservoir using the time-frequency spectrum component. The energy of thin layers' reflection moves to higher frequency, which is taken into consideration to detect the thin sand pinch-out point. Compared with the conventional method that only use the amplitude of seismic, the proposed method improves the accuracy of pinch-out point detection. Tests on models proves the validity of the proposed method for identifying the sharp vanishing point of thin sand layers. Finally, good results of pinch-out boundary detection in real case application strengthen the practicability and reliability of our method.

matching pursuit; pinch-out line detection; thin sand bed; time-frequency analysis

2017-08-24 改回日期： 2017-09-05

“十二五”國家科技重大專項(2011ZX05023-002-007)

汪瑞良(1960-)，男，教授級高級工程師，主要從事地球物理方法研究及其在油氣勘探開發中的應用，E-mail：wangrl@cnooc.com.cn。

1001-1749(2017)06-0799-09

P 631.4

A

10.3969/j.issn.1001-1749.2017.06.13