基于ANSYS的永磁同步電機的設計與仿真

侯 鵬, 周國鵬, 萬仁卓, 周 芳, 周 智

(1. 武漢紡織大學 電子與電氣工程學院, 湖北 武漢 430200;2. 湖北科技學院 工程技術研究院, 湖北 咸寧 437100)

基于ANSYS的永磁同步電機的設計與仿真

侯 鵬1,2, 周國鵬2, 萬仁卓1, 周 芳2, 周 智2

(1. 武漢紡織大學 電子與電氣工程學院, 湖北 武漢 430200;2. 湖北科技學院 工程技術研究院, 湖北 咸寧 437100)

為了簡化研發永磁電動機的設計周期, 本文提出了一種基于Ansys Maxwell軟件RMxprt電磁計算模塊的建模與仿真方法。 以550w永磁同步電機(PMSM)為例, 首先利用基于磁路法對電機進行電磁計算, 用RMxprt模塊對電機本體建立幾何模型, 然后利用Maxwell2D進行瞬態和負載穩態運行有限元計算與分析, 驗證了電磁設計的合理性, 同時比較了基于磁路法RMxprt的計算和Maxwell2D有限元分析相結合的電機設計過程。 結果表明, 有限元分析法的精度優于磁路法, 該分析方法能夠為永磁同步電機設計提供一種有效途徑, 同時也為永磁同步電機的進一步優化提供了理論依據。

永磁同步電機；Ansys Maxwell；磁路法；有限元分析；瞬態仿真

永磁同步電動機(Permanent Magnet Synchronous Motor, PMSM)運行時,在它的內部存在著電磁場,這個電磁場由定子電流、永磁體所產生,電機內電磁場的分布決定了電機性能的好壞,因此計算和仿真分析電機內部的電磁場對設計電機本體具有重要的意義[1]。

對電機內部電磁場的傳統分析方法是建立在磁路法的基礎上, 通過經驗參數和實驗修正進行數值計算, 計算精度不能滿足現代電機設計的要求。文獻[2]應用了磁路法外加各種系數修正對異步電機的結構設計進行了仿真與分析。 文獻[3]采用等效磁路法與數值解法相結合的計算方法對多種永磁電機的原理進行了深入的研究。 有限元數值解法實質是將連續磁場變為離散磁場來研究,把所求電磁場區域剖分成有限多的網格,將電機模型離散化, 有限元分析法精度高,適用面廣。 文獻[4]采用了有限元法對單相永磁同步電機進行了仿真研究。 在國外, Lipo等在文獻[5]中應用場路耦合有限元法仿真了永磁同步電機的穩態運行性能, Gieras等在文獻[6]中用有限元法計算了同步電動機的參數和性能, 文中參數仿真能真實地反映負載時磁場的飽和程度。 總之, 國內外學者對各種電機電磁場性能仿真分析取得了一些成果, 很明顯利用有限元法分析電機磁場更精確, 但利用有限元法分析各種電機模型還有待完善。

本文將采用有限元法對永磁同步電機(PMSM)內部電磁場進行數值計算與仿真分析。首先基于RMxprt模塊建立永磁電機的數學模型, 然后將RMxprt模塊生成的幾何模型導入Maxwell2D模塊, 利用Maxwell2D模塊對電機進行有限元仿真與分析, 驗證電機設計的合理性, 并為進一步優化打下基礎。

一、永磁同步電機主要尺寸的確定

電機電磁設計需要確定很多尺寸, 而最重要的是電機的電樞鐵心直徑D和長度L。 永磁同步電機主要尺寸的確定與非永磁電機的方法相似, 主要根據永磁同步電機電磁計算確定各部分尺寸, 根據下面公式可以確定電機的電樞直徑D和鐵心長度L:

式中:p—計算功率;A—電負荷;Bσ—氣隙磁通密度;αi—極弧系數;kφ—氣隙磁通波形系數;kdp—繞組系數。

通過基于磁路法的電磁計算確定了電機的尺寸數據如表1所示。

表1 PMSM額定數據和尺寸

二、永磁同步電機模型的建立

根據PMSM的額定數據和尺寸在Ansoft RMxprt 模塊中生成的幾何模型, 導入到Maxwell2D模塊中生成如圖1所示的初始幾何模型, Maxwell2D模塊生成的模型將進一步進行瞬態場求解。

圖1 永磁電機幾何模型圖

三、有限元仿真求解器的設置

為了能保證基于場的有限元求解精度,需要在Analysis菜單中選擇set solver option進行求解方式和精度的設置。 設置初始速度為額定轉速1500r/min, 步長為0.01ms, 仿真時間4ms, 通過Maxwell瞬時求解器的設置來完成550w永磁同步電機的性能仿真。 圖2為電機剛起動時電機內部磁力線的變化,可以看出電機運行0.025s后電機定子槽內漏磁增加, 如圖3所示。 通過圖1與圖2磁力線分布圖直觀地判斷出電機內部磁場的分布是合理的, 沒有飽和, 為優化電機的電磁計算奠定了基礎。

圖2 運動初始時刻的磁密矢量圖

圖3 運動0.025s時的磁密矢量圖

1.空載電磁場分析

永磁同步電機空載磁路是指電機的電樞電流為零時, 永磁體磁場所經過的磁路, 因此應該將電機的激勵源電樞電流設為零, 對電機內部只有永磁體產生的磁場進行有限元計算與分析。

在永磁同步電機中, 氣隙函數是氣隙距離隨轉子相對于定子空間位置變化而變化的函數。 氣隙函數用ge(φ)表示[7], 氣隙函數以360°電角度為周期, 在一個周期內空載氣隙磁密函數的表達式為:

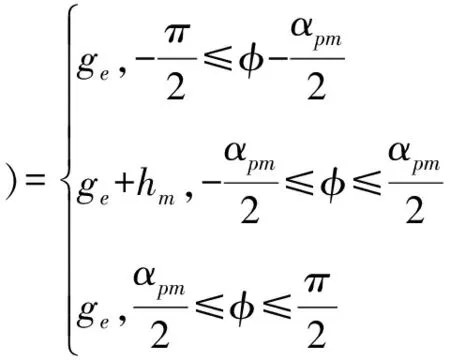
式中αpm為電機有效極弧角度(磁鋼展開角)。 對空載氣隙磁密函數進行傅里葉變換, 得到:

式中,BPMh為永磁氣隙磁密h次諧波幅值;θPM為轉子位置角。

由上式可知, 空載氣隙磁密只含奇數次諧波, 電機的有限元法分析空載氣隙磁密波形如圖4所示, 空載氣隙磁密波形的頂部出現畸變, 對電機的平穩運行不利。 這是由于電機的定子齒與磁極對齊時兩齒間定子槽處的磁阻較大引起的。 通過適當的減小槽口寬度, 增加極靴與磁極的正對面積來改善氣隙磁場分布, 從而減小定子槽處的磁阻, 減小氣隙磁密頂部的畸變[8]。 對比圖4與圖5,基于磁路法的模型的分析結果與實際有一定的偏差。

圖4 有限元計算空載氣隙磁密波形

圖5 基于磁路法的氣隙磁密波形

2.氣隙磁場波形的優化

在氣隙大小為7mm的情況下, 磁路中的磁動勢隨著永磁體厚度的增加而增大, 電機的氣隙磁密也會隨之增大。 但也不能無限地增大下去, 因為電機定子鐵心會隨著磁密的增加而趨于飽和, 故選擇合適的永磁體大小非常有必要。

從圖6中可得到, 隨著永磁體厚度的增加, 電機氣隙磁密形狀基本不變, 但是氣隙磁密也隨之增加, 考慮到磁路飽和的情況, 永磁體厚度為3.5mm時氣隙磁密是最好的。

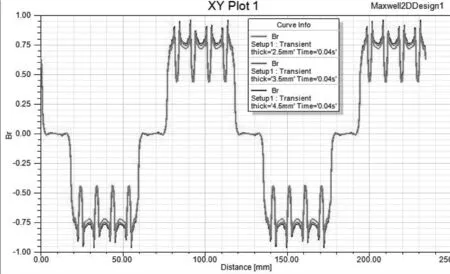
圖6 不同永磁體厚度下氣隙磁密大小

3.空載反電動勢分析

電機各匝線圈的空間分布是關于沿氣隙圓周上電角度φ的函數[9], 將繞組函數定義為:

對其進行傅里葉展開, 得到:

式中φh為繞組函數h次諧波相位角。

永磁磁鏈可由繞組函數和空載氣隙磁密的積分得到, 其表達式為:

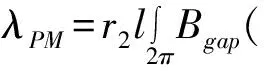
相應永磁電機A相的永磁磁鏈表達式為:

空載反電動勢由永磁磁鏈對時間的偏導數得到, 其表達式為:

相應永磁電機A相的空載反電動勢為:

圖7 空載A相反電動勢

通過上式可知空載反電動勢的諧波成分與電機繞組函數和空載氣隙磁密的諧波成分有關, 我們給定子繞組端懸空, 按額定轉速運行, 得到由空載氣隙磁通在電樞繞組中感應產生的空載反電動勢如圖7所示。 從圖中可清晰看出, 空載反電勢基本按正弦變化,周期與幅值也符合設計要求, 從側面也驗證了電機繞組設計的合理性, 但從圖8中可以看出A相反電動勢含有一定的諧波分量,這是因為一方面電機開有齒槽, 導致磁導不均勻, 感應出齒諧波電動勢; 另一方面鐵芯和轉子都是非線性的, 可以通過提高氣隙磁密正弦度、定子斜槽、使用分布繞組、優化永磁體的布置形式和位置以及改善主極磁場分布等來消除諧波。

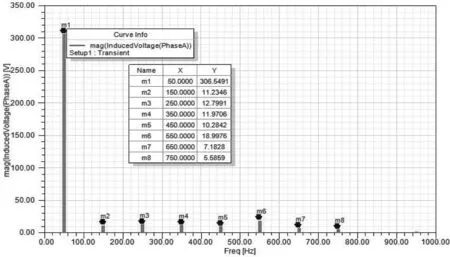
圖8 空載A相反電動勢頻譜特性

表2 PMSM空載A相反電動勢幅值

由上表可知, 永磁同步電動機中產生電磁轉矩的永磁磁鏈有效分量主要是其基波分量, 永磁磁鏈基波部分表達式為:

λPM1=r2lπBPMN1cosθPM

故空載反電動勢基波部分為:

epl=ωer2lπBPMN1sinθPM

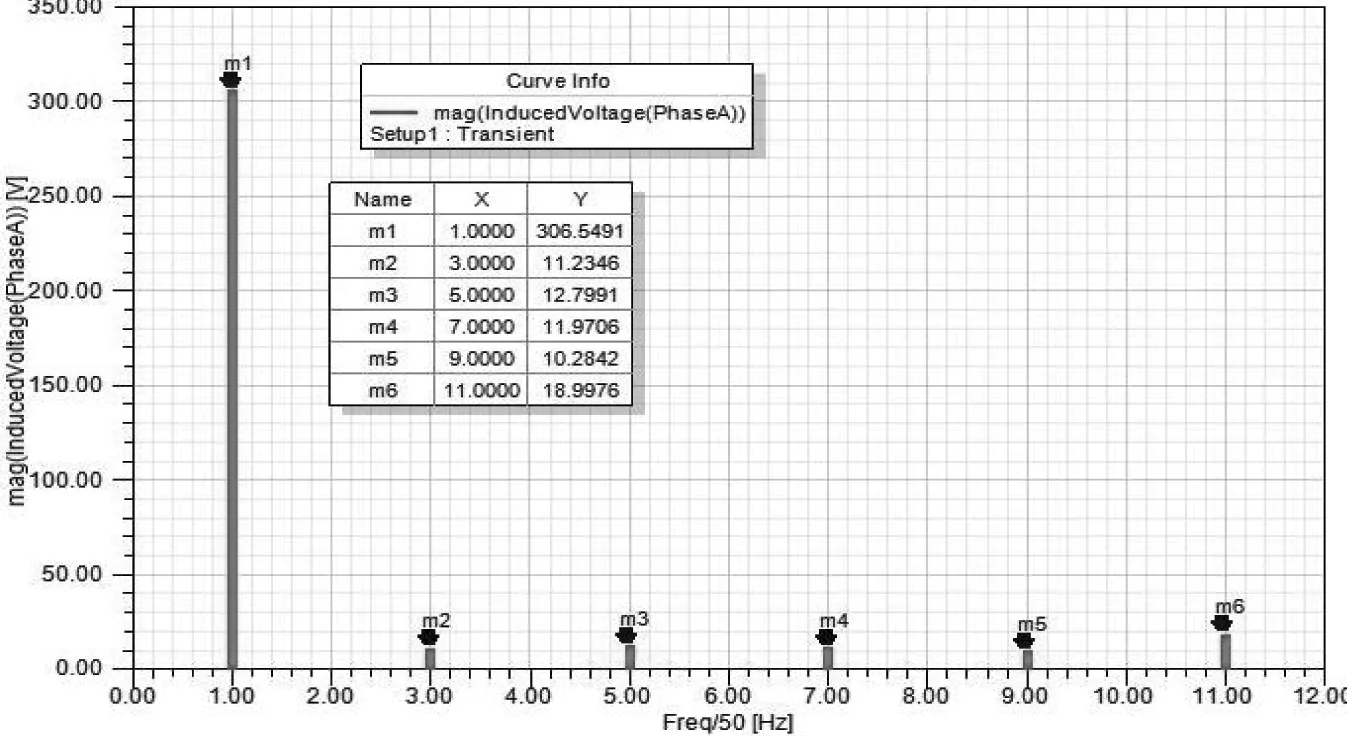
圖9 空載A相反電動勢各次諧波幅值

由以上公式可計算出A相空載反電動勢波形的諧波幅值, 與表2基本一致。 觀察電機諧波頻譜圖9, 可清晰的看出電機的3、5、7、9、11次諧波及幅值, 在空載狀態下, 3次諧波幅值較高, 而諧波幅值的大小也隨著諧波次數的增大而減小, 越是高次諧波由于幅值很小對電機的影響也越來越小, 還可以對諧波進行快速傅里葉變換, 將反電動勢頻譜轉換為傅里葉分解, 將信號的頻譜由波形中提取出來。 反電勢幅值接近額定電壓, 電機額定運行時效率越高, 設計就越合理。

4.瞬態場分析

Maxwell2D模塊默認生成的模型將進行瞬態場仿真求解, 可以得出轉軸上的電磁轉矩如圖10, 對轉矩進行諧波傅里葉分解,各次諧波幅值如圖11, 通過計算可知高次諧波轉矩相對基波轉矩為15%左右, 觀察圖10可得電磁轉矩有一定脈動性, 這在誤差允許的范圍內, 引起這種情況的主要因素是電網電源存在的一定量的諧波。

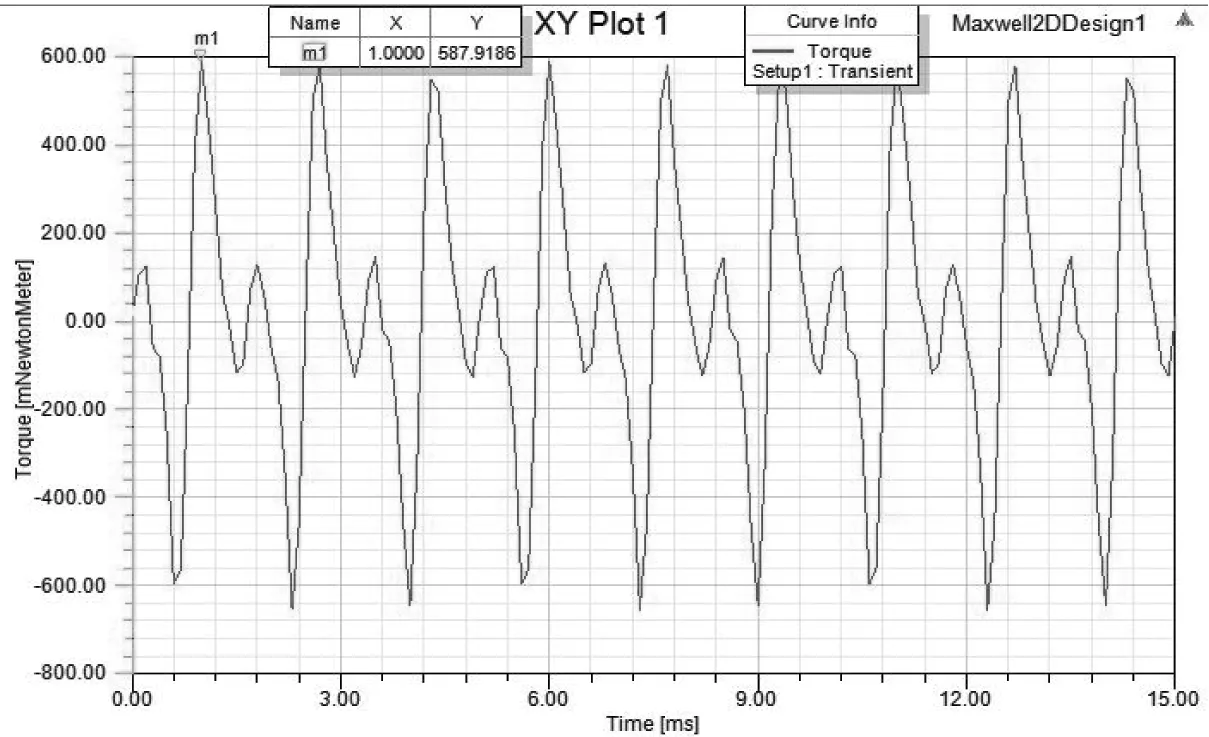
圖10 轉矩特性曲線

圖 11 轉矩頻譜特性

5.額定狀態分析

利用Maxwell2D模塊默認生成的模型進行瞬態場仿真求解分析, 從而模擬電機的性能表現。 額定狀態下, 電磁轉矩、定子電流的波形分別如圖12、圖13所示, 圖14是磁鏈曲線, 明顯發現電機反電動勢波形與定子電流波形類似, 實際反電動勢并不完全是正弦波形, 有一定量的頂部失真, 對于直接轉矩控制的無刷的直流電機正是利用反電動勢波形頂部失真來確定換相點的。

圖12 額定轉速點下瞬態電磁轉矩

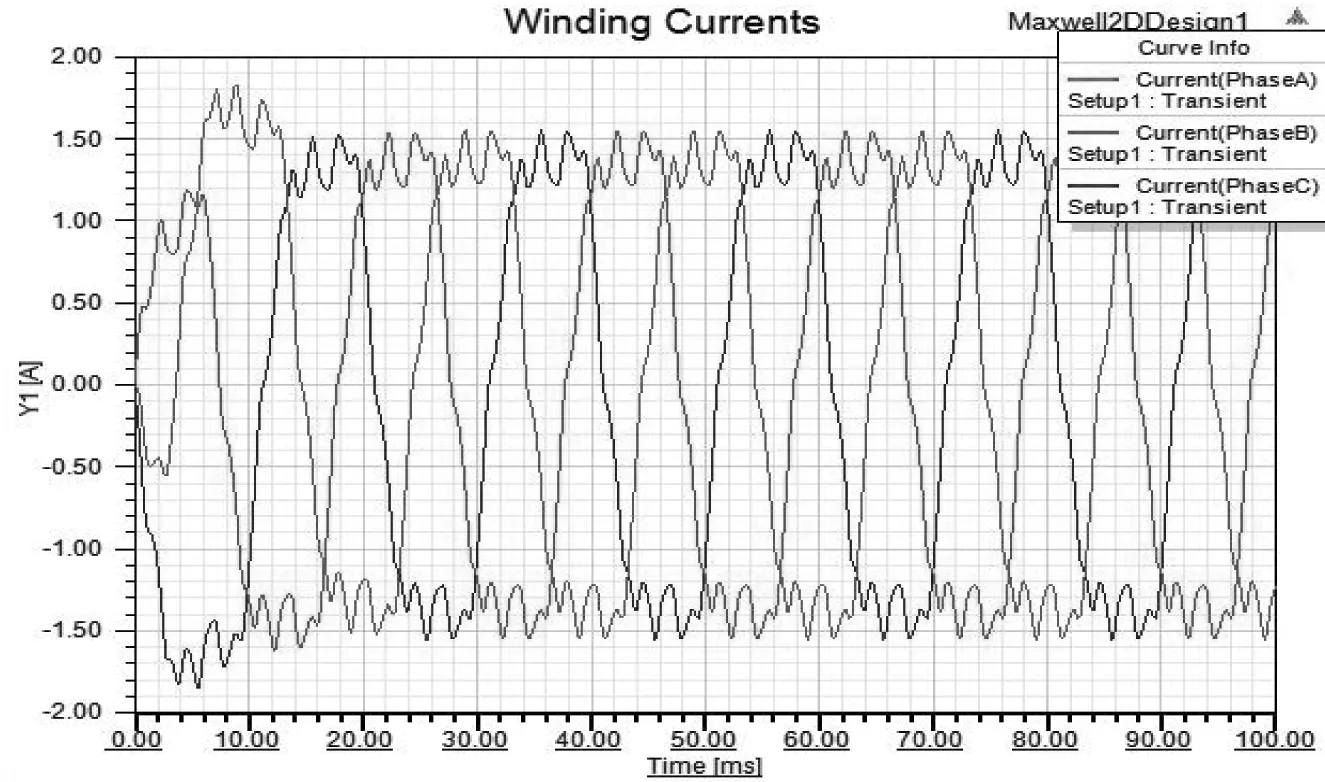
圖13 額定轉速點下的定子電流波形

圖14 額定轉速點下的繞組磁鏈曲線

四、結語

本文首先用磁路法確定了永磁同步電動機的基本尺寸, 然后在Ansys Maxwell RMxprt模塊中建立了電機基本模型, 一鍵生成二維瞬態仿真模型, 對電機內部只有永磁體單獨產生的磁場進行有限元分析, 并對永磁體厚度進行參數化計算分析, 同時用有限元法對各種參數進行了計算, 得出了空載反電動勢,根據波形可以得出波形為正弦, 但有少量的諧波, 證明繞組設計是合理的, 最后借助Ansoft Maxwell 2D模塊對永磁同步電動機的額定狀態下運行性能進行了分析和仿真, 得到了電磁轉矩曲線、定子電流波形、輸繞組磁鏈曲線和數據, 對優化同步電機性能具有重要意義。

[1] 黃明星. 新型永磁電機設計、分析與應用研究[D]. 杭州：浙江大學, 2014.

[2] 黃國. Y2系列三相異步電動機技術手冊[M]. 北京：機械工業出版社, 2011.

[3] 唐任遠. 現代永磁電機理論與設計[M]．北京: 機械工業出版社, 2010.

[4] 唐明. 基于Maxwell 2D的單相永磁同步電動機仿真研究[J]. 微電機, 2013, 38(5), 28～30．

[5] Gieras J.F. Wing M. Permanent Magnet Motor Technology: Design and Applications Second Edition [M]. New York: Marcel Dekker, 2014.

[6] Lipo T.A. Introduction to AC Machine Design[M]. Wisconsin Power Electronics Center, University of Wisconsin, 2007.

[7] 趙博, 張洪亮. Ansoft12在工程電磁場中的應用[M]. 北京: 中國水利水電出版社, 2010.230～335.

[8] 唐任遠. 特種電機原理及應用[M]. 北京: 機械工業出版社, 2010.

[9] 許實章. 電機學[M]. 北京: 機械工業出版社, 2005.

2095-4654(2017)06-0146-05

2017-09-19

NSFC-浙江兩化融合聯合基金項目(U1509217)；湖北省科技支撐計劃項目(2015BAA001)；湖北省中小企業科技創新基金(2015DAL069)；湖北省教育廳科技計劃項目(Q20142803)

T351

A

吳惠娟