基于機器學習的PM2.5短期濃度動態預報模型

戴李杰，張長江，馬雷鳴

(1.浙江師范大學 數理與信息工程學院，浙江 金華 321004； 2.上海市氣象局 中心氣象臺，上海 200030)

基于機器學習的PM2.5短期濃度動態預報模型

戴李杰1，張長江1*，馬雷鳴2

(1.浙江師范大學 數理與信息工程學院，浙江 金華 321004； 2.上海市氣象局 中心氣象臺，上海 200030)

針對目前現有的PM2.5模式預報系統的預報值偏離實際濃度較大的問題，從上海市浦東氣象局獲得2015年2月至7月的PM2.5實況觀測濃度、PM2.5模式預報(WRF-Chem)濃度和5個主要氣象因子的模式預報數據資料，聯合應用支持向量機(SVM)和粒子群優化(PSO)算法建立滾動預報模型，對PM2.5未來24小時濃度進行預報，同時對未來一天的晝、夜均值及日均值濃度進行預報，并與徑向基函數神經網絡(RBFNN)、多元線性回歸法(MLR)、模式預報(WRF-Chem)作對比。實驗結果表明，相比其他預報方法，所提出的SVM模型較大提高了PM2.5未來1小時濃度預報精度,這與此前的研究結論相符; 所提模型能對PM2.5未來24小時濃度進行較好的預報，能對未來一天的晝均值、夜均值及日均值進行有效預報，并且對未來12小時的逐時濃度及未來一天的夜均值濃度的預報準確度較高。

機器學習;粒子群優化算法;動態模型;滾動預報

0 引言

目前PM2.5濃度預報的研究在中國才剛剛起步，觀測數據資料缺乏，PM2.5濃度的預報手段比較粗糙，實際預報效果不盡如人意。現階段，對于PM2.5濃度的預報主要包括數值模式預報和統計預報兩種方法。由于數值模式預報對污染與氣象數據的要求較高，而大量詳細的相關數據往往很難獲得[1]，所以數值模式預報方法在中國大多城市并不成熟。目前，主要通過統計模型對PM2.5濃度進行預報，主要包括回歸模型(線性和非線性回歸模型)、神經網絡模型、支持向量機(Support Vector Machine, SVM)模型及馬爾可夫模型等。

回歸模型在氣象預報領域是一種有效和廣為使用的方法，近年來被較多應用于PM2.5濃度預報。如Cobourn[2]提出一種基于非線性回歸和后推氣流軌跡濃度的預報模型來預報PM2.5濃度日均最大值。Baker等[3]使用非線性回歸模型對單一排放來源的PM2.5濃度進行預報。

人工神經網絡(Artificial Neural Network, ANN)能較好地解決非線性問題，具有自學習功能，近年來也被應用于PM2.5濃度預報，其中尤以反向傳播神經網絡(Back Propagation Neural Network, BPNN)及徑向基神經網絡(Radical Basis Function Neural Network, RBFNN)較為常用。如：Zhang等[4]用變化隱含層神經元數量來改進BPNN，并用地理信息系統來評估不同算法的PM2.5濃度預報效果，結果顯示當隱含層神經元數量為20時有較高的精度；Wu等[5]將氣溶膠光學厚度、邊界層高度、相對濕度、溫度、風速、風向及月份作為神經網絡的輸入，利用基于貝葉斯規則的BPNN對PM微粒(PM1、PM10和PM2.5)進行研究分析。有學者使用RBFNN應用于PM2.5濃度預報，如：Zheng等[6]用RBFNN建立靜態預報模型，選擇8個影響因子作為訓練輸入，相應時間的PM2.5濃度值作為訓練輸出，結果表明RBFNN模型的預報能力優于BPNN模型。近年來，有學者將ANN與其他智能技術相結合應用于PM2.5濃度預報，如：Zhou等[7]建立基于總體平均經驗模式分解和廣義回歸神經網絡的混合預報模型，預報西安市未來一天的日均PM2.5濃度； Feng等[8]將基于軌道的地理參數作為神經網絡的輸入，用氣團軌跡分析和小波變換的方法來提高ANN的性能，預報未來兩天的PM2.5日平均濃度值，結果表明該混合模型有效地提高了預報準確度并具有預報高峰點濃度值的能力；Voukantsis等[9]建立線性回歸與ANN混合的模型對PM10及PM2.5未來一天的日均值進行預報；Mishra等[10]將神經網絡與模糊邏輯相結合，對德里市區的PM2.5濃度進行預報，所建立的模糊神經網絡模型優于ANN模型和多元線性回歸法(Multiple Linear Regression, MLR)模型。

近年來SVM逐漸被成功應用于對PM2.5的濃度進行預報，如：李龍等[11]選擇綜合氣象指數、二氧化硫濃度、一氧化碳濃度、二氧化氮濃度和PM10濃度構成特征向量，并利用特征向量和PM2.5濃度數據來建立最小二乘支持向量機預報模型，結果表明該模型能夠較為準確地預報PM2.5濃度，泛化能力較強。劉杰等[12]提出應用SVM和模糊粒化時間序列相結合的方法，以北京市城六區海淀萬柳監測點為例，結果表明基于模糊粒化時間序列的預報模型能較好解決PM2.5機理性建模方式下由于影響因素考慮不全而造成的預報結果不穩定。

雖然上述國內外學者使用SVM對PM2.5濃度進行預報，但是所建立的模型基本上為靜態模型，采用固定的數據進行訓練，然后用測試數據進行預報。

除了上述基于回歸方程、神經網絡和SVM等技術外，近年來一些其他智能技術也被成功應用于PM2.5濃度預報的領域中，如：Sun等[13]提出改進的隱馬爾可夫模型來預報日平均濃度，他們把重點放在PM2.5高濃度時間段，預報兩個地區的PM2.5濃度過高的時期； Yang[14]使用橢圓軌道模型對日均PM2.5濃度的變化進行預報，并將此方法用在湘潭監測站的日均PM2.5濃度變化的預報，利用前6天的日均值數據來建立模型，預報下一天的PM2.5日均濃度值。

綜上所述，由于PM2.5與空氣質量、氣象因子之間一般來說是非線性的關系，雖然神經網絡能較好地解決非線性關系問題，非線性擬合能力較強，但仍然存在一些問題，其學習速度慢、容易過擬合和陷入局部極小值等問題都會導致預報結果的不準確。SVM在解決小樣本、非線性及高維模式識別中表現出許多特有的優勢，可用于模式分類、非線性回歸和時間序列預報等。目前對PM2.5濃度進行預報進行的研究，所建立的模型基本上為靜態模型。本文提出新的PM2.5濃度預報方法，在此之前，已完成研究應用SVM建立PM2.5未來一小時濃度動態預報模型，利用粒子群優化(Particle Swarm Optimization, PSO)算法輔助尋找適用于每次預報模型的最優SVM參數，實驗結果表明SVM模型的預報精度最優，并且對PM2.5濃度變化劇烈的情況具有較好的預報能力[15]。之后，完成研究聯合應用SVM和PSO建立滾動預報模型，預報PM2.5未來12 h濃度值及未來一天的夜均值濃度，實驗結果表明SVM模型的預報精度最高[16]。在此研究基礎上，由于人類生產生活具有晝夜的區分，則對未來白天和夜晚的PM2.5濃度均值的預報將比日均值更具指導意義，本文將PM2.5模式預報數據與5個主要氣象影響因子模式預報數據結合使用，聯合應用SVM和PSO建立滾動預報模型，對PM2.5未來24 h濃度進行逐時預報，同時對未來一天的晝、夜均值及未來一天的日均值濃度進行預報。本文所采用的方法是建立動態預報模型，每次建模訓練的數據及SVM參數都是動態變化的，即每次預報時，都建立不同的動態模型，以提高PM2.5濃度預報的準確度。

1 數據及預報方法

1.1 數據選取與處理

數據是由上海浦東氣象局所提供的歷史小時數據(2015年2月3日至7月15日)，包括PM2.5實況觀測值、PM2.5模式預報(WRF-Chem)濃度及2 m高度處溫度(Temperature, T2)、2 m高度處相對濕度(Relative Humidity, RH2)、風速(Wind Speed, WS)、風向(Wind Direction, WD)、海平面氣壓(Sea Level pressure, SLVL)等模式預報的氣象要素數據。經過統計分析得出小時PM2.5濃度與該5個主要因子相關性較大，本文選擇此5個氣象因子(T2、RH2、WS、WD、SLVL)及PM2.5模式預報值作為預報PM2.5未來24 h建模的訓練輸入，訓練輸出為相應時刻的實況觀測值，以此可建立未來24 h的滾動預報模型。本文使用模式預報中每日20:00(北京時間)起報數據，利用模式每次預報未來24 h的PM2.5模式預報值及5個氣象因子模式預報數據，即每次預報時間段為21:00時至次日20:00時。

在訓練之前，先對數據進行歸一化處理，將數據都歸一化到[0,1]，可消除各維數據之間的數量級差別，有利于提高模型的預報精度，所用到的歸一化函數為：

xk=(xk-xmin)/(xmax-xmin)

(1)

式中：xmin為數據序列中的最小值；xmax為數據序列中的最大值。

1.2 訓練建模所用樣本量選擇

本文聯合應用SVM和PSO建立PM2.5未來24 h的滾動預報模型，訓練數據分別選擇前18 h至前48 h，得到不同訓練建模數據的PM2.5預報的平均絕對誤差(Mean Absolute Error, MAE)及平均相對誤差(Mean Relative Error, MRE)。本文利用2015年2月3日至7月15日的數據進行分析，尋找最適合預報PM2.5未來24 h濃度值的訓練建模所用數據量。首先選擇2月4日20：00為第一次起報，每次預報未來24 h濃度值，每日20:00預報一次，以此類推，直到7月15日20:00最后一次起報，共162次預報數據。若選擇2月4日為第一次預報，則訓練建模數據量可從前18 h至前24 h，最終可得162次預報數據。若選擇2月5日為第一次預報，則訓練建模數據量可從前25 h至前48 h，最終可得161次預報數據。誤差曲線如圖1所示。

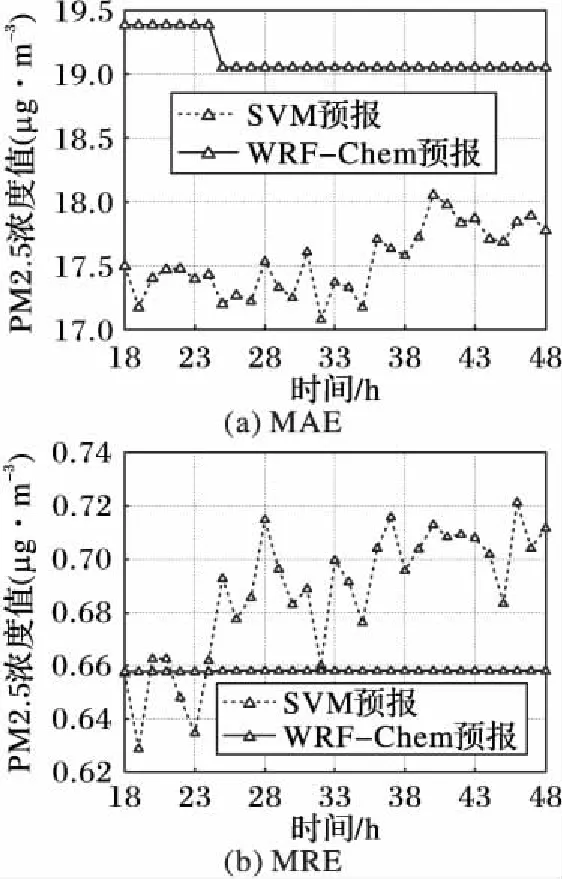
圖1 采用不同樣本量建模的誤差曲線Fig. 1 Error curve of using different sample size for modeling

對于圖1(a)中采用不同樣本量作為訓練建模時的SVM模型的誤差曲線，第一個點為使用前18 h的數據量進行訓練建模，對162次預報(每次預報未來24 h)的MAE進行平均運算后所得數據，以此類推，得到訓練數據量分別從前19 h至前48 h的誤差曲線。圖1(b)中SVM模型的誤差曲線為相同方法下所得的MRE曲線。由圖1可知，對于預報未來24 h濃度，當訓練建模數據量為前19 h時，MAE較小，MRE最小，因此選取待預報時刻的前19 h的歷史數據量作為訓練建模的數據量。

1.3 ε-支持向量機非線性回歸

利用SVM進行非線性回歸和預報是將數據通過非線性映射到高維特征空間Ω中，即將低維線性不可分問題轉化至高維中線性可分，在該特征空間中進行線性回歸。

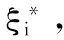
(2)

(3)

式中，C為懲罰常數，用于控制對超出誤差范圍的樣本的懲罰程度。然后用拉格朗日乘子法求解，將原空間中的非線性回歸問題轉化為高維特征空間中的線性回歸進行求解，基本思想是將高維特征空間中的向量內積φ(xi)·φ(x)用輸入空間中的核函數K(xi,x)來替代[18]，即:

K(xi,x)=φ(xi)·φ(x)

(4)

回歸函數可以寫為：

(5)

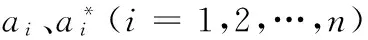
本文基于2015年2月至7月的氣象數據資料，使用Matlab語言編程，用SVM、RBFNN和MLR分別建立預報模型。SVM類型選擇epsilon-SVR，核函數選擇RBF核函數，其中利用PSO優化SVM的懲罰參數c和核函數中的系數γ，通過交叉驗證的方法選擇最佳參數c和γ，然后用選定的參數進行訓練建模，用訓練好的模型進行預報。

2 粒子群優化算法

粒子群優化(PSO)算法中每個粒子代表問題的一個潛在解，用位置、速度和適應度值三項指標來表示該粒子的特征，速度影響粒子的運動方向和距離，適應度值由適應度函數計算所得。在每次迭代過程中，粒子通過個體極值和種群全局極值來更新自身速度和位置，公式如下：

(6)

(7)

式中:ω為慣性權重；d=1,2,…,D;i=1,2,…,n;k為迭代次數；Vid為粒子的速度;Xid為粒子的位置；c1和c2為學習因子；r1和r2為分布于[0,1]的隨機數。

慣性權重ω描述了粒子的慣性對于速度的影響，其取值大小可以調節PSO算法的全局與局部尋優的能力。You等[19]指出隨著迭代次數的增加，慣性權重逐漸減小，算法的局部尋優能力越來越強，但也有可能會陷入局部最優，他們提出了自適應慣性權重的策略，隨著迭代次數的增加，慣性權重將自動改變，表達式為：

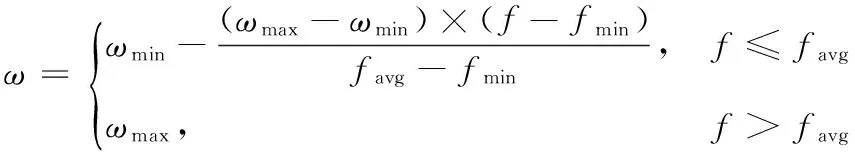
(8)

式中:ωmax和ωmin表示慣性權重的最大值和最小值，f表示當前的目標函數值，favg和fmin表示當前所有微粒的平均目標值和最小目標值，權重值ω會隨著目標函數值而自動地改變，當各粒子的目標值趨于一致或局部最優時，將使慣性權重增加，從而避免陷入局部最優；當各粒子的目標值比較分散時，將使慣性權重減小，有利于粒子靠近最優粒子。該自適應改變慣性權重策略可有效地提高全局和局部尋優能力。在大多數的應用中，ωmax=0.9，ωmin=0.4時，算法性能最好。

粒子群算法存在容易早熟收斂的缺點，當遇到多峰問題時易陷入局部最優解。借鑒遺傳算法中的變異思想，將變異算子引入粒子群算法，即對某些變量以一定的概率重新初始化。本文在粒子群算法的基礎上引入變異算子，在每次速度和種群更新過后，以一定的概率重新初始化粒子，使新粒子可以重新在更大空間中進行尋優，增強粒子群算法的尋優能力。

3 預報模型的建立

基于上海浦東氣象局獲得2015年2月— 7月的PM2.5實況觀測濃度、PM2.5模式預報(WRF-Chem)濃度和5個主要氣象影響因子的模式預報數據資料，在PM2.5模式預報數據的基礎上，加入另外5個主要氣象影響因子模式預報數據，聯合應用SVM和PSO建立滾動預報模型，對PM2.5未來24 h濃度進行預報，同時對未來一天的晝、夜均值及未來一天的日均值濃度進行預報。

具體方案如下：

1)采用三次樣條插值方法對所獲得的數據(2015年2月— 7月)中少量的缺失數據進行插值，然后對數據進行歸一化預處理。

2)利用SVM與RBFNN、MLR分別進行建模，將模式下PM2.5濃度預報值和同時刻5個氣象影響因子模式預報值作為訓練輸入，相應時刻的PM2.5實況觀測值作為輸出，訓練數據量取前19 h的數據。

3)對于已建好的模型，導入未來一個小時PM2.5及5個氣象影響因子模式預報值，預報未來一小時PM2.5濃度值。

4)將預報所得的PM2.5濃度值作為該時刻的實況值，作為預報下一個小時濃度的建模所用，可預報PM2.5下一個小時濃度值，以此建立滾動預報模型，然后轉步驟3)直至預報到24 h為止。

5)將預報所得的未來24 h濃度值的前12 h(21:00至次日8:00)和后12 h(次日9:00至20:00)分別作平均運算，得到未來夜均值和晝均值；將預報所得的未來24 h(21:00至次日20:00)濃度值作平均運算，得到未來一天的日均值濃度。

基于機器學習的PM2.5濃度滾動預報模型流程如圖2所示。

4 實驗結果及分析

本文使用Matlab語言編程，用SVM、MLR和RBFNN分別建

立預報模型。最終經實驗得出未來24 h、未來一天的夜均值、晝均值及未來一天的日均值濃度預報曲線、絕對誤差柱狀圖。

圖2 基于機器學習的PM2.5濃度滾動預報模型Fig. 2 Rolling forecasting model of PM2.5 concentration based on machine learning

4.1 預報未來一天的PM2.5夜均值及晝均值

4.1.1 預報曲線及誤差柱狀圖

2015年2月— 7月的夜均值及晝均值濃度預報曲線如圖3所示。2015年2月— 7月的夜均值及晝均值絕對誤差柱狀圖如圖4所示。

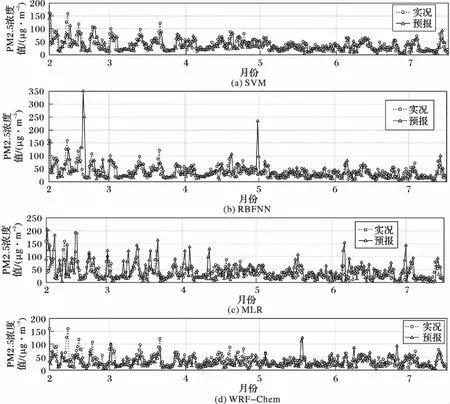
圖3 PM2.5夜均值及晝均值濃度預報曲線Fig. 3 Forecasting curve of nighttime and daytime average concentration

由圖3可知，對于PM2.5未來一天的夜均值及晝均值濃度，各種方法的預報曲線與實際觀測曲線的趨勢都相似。SVM模型的預報曲線與實際觀測曲線最為接近，尤其在濃度轉變的波峰波谷附近，該模型仍能較好地進行預報。WRF-Chem預報曲線的前半部分相比實際觀測曲線偏低。RBFNN模型的預報曲線有少數偏離實況觀測值較大，整體趨勢與實際觀測曲線相似。MLR模型的預報曲線有較多的點偏離實際觀測曲線，預報效果不理想。相比之下，SVM模型的預報曲線與實際觀測曲線的趨勢最為接近。

由圖4可知，對于PM2.5未來一天的夜均值及晝均值濃度，絕對誤差落在最小誤差區間(-5,5]的頻數最多的是SVM預報模型。WRF-Chem預報的誤差柱狀圖中，落在誤差區間(-15,-5]的頻數最多。RBFNN模型和MLR模型預報的誤差柱狀圖中，落在最小誤差區間(-5,5]的頻數最多，但RBFNN模型的預報中有少數落在誤差較大的區間，偏離實況觀測值較大。各種預報方法的MAE從小到大依次是SVM模型、WRF-Chem、RBFNN模型和MLR模型。相比之下，對于PM2.5未來一天的夜均值及晝均值濃度，SVM模型的預報精度最高，并且算法穩定性最好。

圖4 PM2.5夜均值及晝均值絕對誤差柱狀圖Fig. 4 Absolute error histogram of nighttime and daytime average concentration

4.1.2 誤差分析

夜均值及晝均值誤差數據如表1所示，夜均值誤差數據如表2所示。

表1 夜均值及晝均值MAE μg/m3Tab. 1 MAE of nighttime and daytime average concentration μg/m3

由表1可知，對于未來一天的夜均值及晝均值濃度，SVM模型的MAE比WRF-Chem小，RBFNN模型和MLR模型的MAE比SVM模型和WRF-Chem大，并且RBFNN模型的預報穩定性較差，MLR模型的預報誤差最大。對于2月4日— 7月15日的MAE，從小到大分別是SVM模型、WRF-Chem、RBFNN模型及MLR模型。綜上所述，對于未來一天的夜均值及晝均值濃度，SVM模型的預報精度最高，算法性能穩定。同時發現，對于PM2.5的短期預報(未來一天的夜均值及晝均值濃度)，RBFNN模型的預報精度比MLR模型高。

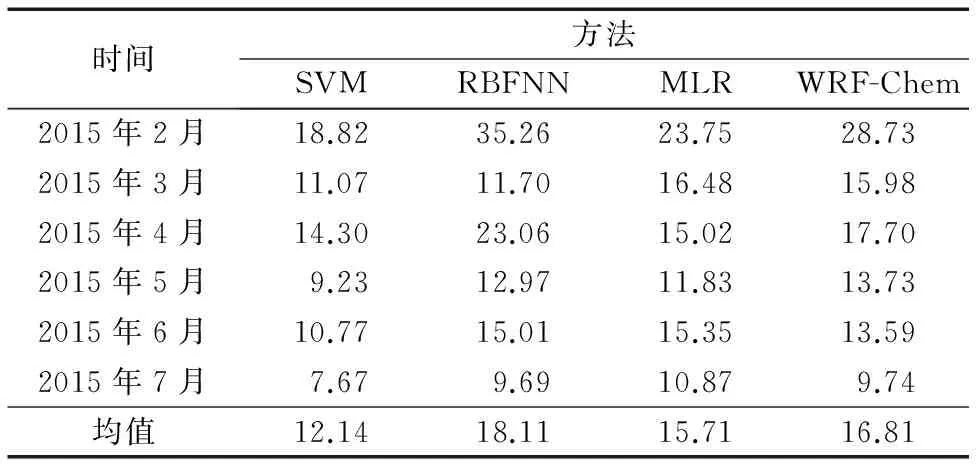
表2 夜均值MAE μg/m3Tab. 2 MAE of nighttime average concentration μg/m3

由表2可知，對于未來一天的夜均值濃度，SVM模型每個月的MAE都比WRF-Chem小，RBFNN模型及MLR模型的MAE比SVM模型和WRF-Chem大，并且 RBFNN模型和MLR模型的預報穩定性較差。對于2月4日— 7月15日的MAE，從小到大分別是SVM、WRF-Chem、RBFNN及MLR。對于未來一天夜均值濃度的預報，SVM模型的預報精度較高，誤差比RBFNN模型、MLR模型及WRF-Chem小。本文所提出的SVM預報模型可以有效地預報未來一天的夜均值濃度，預報誤差相比WRF-Chem預報有一定降低。

4.2 預報未來一天的日均值

4.2.1 預報曲線及誤差柱狀圖

2015年2月— 7月的日均值預報曲線如圖5所示。2015年2月— 7月的日均值絕對誤差柱狀圖如圖6所示。

由圖5可知，對于PM2.5未來一天的日均值濃度，各種方法的預報曲線與實際觀測曲線的趨勢都相似。SVM模型的預報曲線與實際觀測曲線最為接近，尤其在濃度轉變的波峰波谷附近，該方法仍能較好地進行預報。WRF-Chem預報曲線的前半部分相比實際觀測曲線偏低。RBFNN模型的預報曲線有少數偏離實況觀測值較大，整體趨勢與實際觀測曲線相似。MLR模型的預報曲線有較多的點偏離實際觀測曲線，預報效果不理想。相比之下，SVM模型的預報曲線與實際觀測曲線的趨勢最為接近，算法性能最穩定。

由圖6可知，對于PM2.5未來一天的日均值濃度，絕對誤差落在最小誤差區間(-5,5]的頻數最多的是SVM模型。WRF-Chem預報的誤差柱狀圖中，落在誤差區間(-15,-5]的頻數最多。RBFNN模型預報的誤差柱狀圖中，落在最小誤差區間(-5,5]的頻數最多，但有少數點落在誤差較大的區間，偏離實況觀測值較大。各種預報方法的MAE從小到大依次是SVM模型、WRF-Chem、RBFNN模型和MLR模型。相比之下，對于PM2.5未來一天的日均值濃度，SVM模型預報的精度最高，并且算法穩定性最好。

圖5 PM2.5日均值預報曲線Fig. 5 Forecasting curve of daily average concentration

圖6 日均值絕對誤差柱狀圖Fig. 6 Absolute error histogram of daily average concentration

4.2.2 誤差分析

日均值的誤差數據如表3所示。

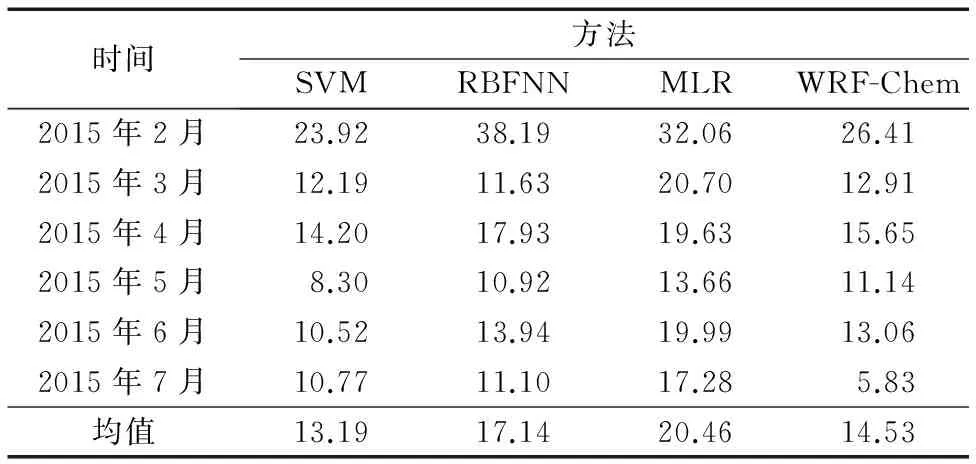
表3 日均值MAETab. 3 MAE of daily average concentration

由表3可知，對于未來一天的日均值濃度，SVM模型的MAE比WRF-Chem小，RBFNN模型預報的穩定性較差，MLR模型的預報誤差最大。相比各個預報方法，本文所提出的SVM模型的預報誤差最小，算法性能最穩定。對于2月4日至7月15日的MAE，從小到大分別是SVM模型、WRF-Chem、RBFNN模型及MLR模型。綜上所述，對于未來一天的日均值濃度，SVM模型的預報準確度最高，算法性能穩定。同時發現，對于PM2.5的短期預報(未來一天的日均值濃度)，RBFNN模型的預報精度比MLR模型高。

5 結語

本文提出基于機器學習的PM2.5短期濃度預報方法，利用氣象影響因子及PM2.5濃度實際觀測數據，聯合應用SVM和PSO建立PM2.5動態預報模型，并對比RBFNN、MLR、WRF-Chem預報效果，經實驗得出如下結論：

1)對于預報未來24 h逐時濃度值，第一個小時的預報精度較高，前12 h的預報誤差相比后12 h更小，本文所提出的SVM模型可以對未來12 h的均值進行有效預報，并且算法性能穩定。由于本文采用滾動預報的方法，預報誤差會不斷累積，不可避免地存在一些不足，而這些問題也是今后努力研究的方向。

2)對于未來一天的夜均值及晝均值濃度，2015年2月— 7月MAE從小到大依次為SVM模型、WRF-Chem、RBFNN模型及MLR模型，體現了SVM在處理高維非線性問題上的優勢。此前已完成的研究表明：在預報未來一小時濃度中，MLR模型的誤差比RBFNN模型小[15]，說明在臨近預報中，MLR模型優于RBFNN模型，而在本文的短期預報中，RBFNN模型優于MLR模型，說明RBFNN模型比MLR模型具有更強的非線性問題的處理能力。本文所提出的SVM預報模型可對未來一天的夜均值(12 h均值)進行較為準確的預報，并且算法性能穩定。若使用模式每日8:00起報的數據，則對未來12 h均值(晝均值)進行較為準確的預報，體現了滾動預報模型的優勢，可為人們出行及生產生活起到指導作用。

3)對于未來一天的日均值濃度，2015年2月— 7月MAE從小到大依次為SVM模型、WRF-Chem、RBFNN模型及MLR模型，體現了SVM在處理高維非線性問題上的優勢。同理說明在臨近預報中，MLR模型優于RBFNN模型，而在短期預報中，RBFNN模型優于MLR模型。相比之下，SVM模型可對未來一天的日均值濃度進行有效預報。

References)

[1] 劉慧君. 武漢市PM2.5污染的演變預測及成因分析和仿真[D]. 長沙: 湖南大學，2014.(LIU H J. Developing pattern prediction， casual analysis and simulation of PM2.5 pollution in Wuhan city [D]. Changsha: Hunan University, 2014.)

[2] COBOURN W G. An enhanced PM2.5 air quality forecast model based on nonlinear regression and back-trajectory concentrations[J]. Atmospheric Environment, 2010, 44(25): 3015-3023.

[3] BAKER K R, FOLEY K M. A nonlinear regression model estimating single source concentrations of primary and secondarily formed PM2.5[J]. Atmospheric Environment, 2011, 45(22): 3758-3767.

[4] ZHANG P, ZHANG T, HE L, et al. Study on prediction and spatial variation of PM2.5 pollution by using improved BP artificial neural network model of computer technology and GIS[J]. Computer Modelling and New Technologies, 2014, 18(12): 107-115.

[5] WU Y R, GUO J P, ZHANG X Y, et al. Synergy of satellite and ground based observations in estimation of particulate matter in eastern China [J]. Science of the Total Environment, 2012, 433(7): 20-30.

[6] ZHENG H M, SHANG X X. Study on prediction of atmospheric PM2.5 based on RBF neural network[C]// Proceedings of the 2013 4th International Conference on Digital Manufacturing and Automation. Piscataway, NJ: IEEE, 2013:1287-1289.

[7] ZHOU Q P, JIANG H Y, WANG J Z, et al. A hybrid model for PM2.5 forecasting based on ensemble empirical mode decomposition and a general regression neural network [J]. Science of the Total Environment, 2014, 496(2): 264-274.

[8] FENG X, LI Q, ZHU Y J, et al. Artificial neural networks forecasting of PM2.5 pollution using air mass trajectory based geographic model and wavelet transformation[J]. Atmospheric Environment, 2015, 107: 118-128.

[9] VOUKANTSIS D, KARATZAS K, KUKKONEN J, et al. Intercomparison of air quality data using principal component analysis, and forecasting of PM10 and PM2.5 concentrations using artificial neural networks, in Thessaloniki and Helsinki[J]. Science of the Total Environment, 2011, 409(7):1266-1276.

[10] MISHRA D, GOYAL P, UPADHYAY A. Artificial intelligence based approach to forecast PM2.5 during haze episodes: a case study of Delhi, India [J]. Atmospheric Environment, 2015, 102: 239-248.

[11] 李龍, 馬磊, 賀建峰,等. 基于特征向量的最小二乘支持向量機PM2.5濃度預測模型[J]. 計算機應用, 2014, 34(8): 2212-2216. (LI L，MA L，HE J F，et al. PM2.5 concentration prediction model of least squares support vector machine based on feature vector [J]. Journal of Computer Applications, 2014, 34(8): 2212-2216.)

[12] 劉杰, 楊鵬, 呂文生,等. 模糊時序與支持向量機建模相結合的PM2.5質量濃度預測[J]. 北京科技大學學報, 2014, 36(12): 1694-1702.(LIU J, YANG P, LYU W S, et al. Prediction model of PM2. 5 mass concentrations based on fuzzy time series and support vector machine [J]. Journal of University of Science and Technology Beijing, 2014, 36(12):1694-1702.)

[13] SUN W, ZHANG H, PALAZOGLU A, et al. Prediction of 24-hour-average PM2.5 concentrations using a hidden Markov model with different emission distributions in Northern California [J]. Science of the Total Environment, 2013, 443(3): 93-103.

[14] YANG Z C. Modeling and forecasting daily movement of ambient air mean PM2.5 concentration based on the elliptic orbit model with weekly quasi-periodic extension: a case study[J]. Environmental Science and Pollution Research, 2014, 21(16): 9959-9972.

[15] 張長江,戴李杰,馬雷鳴. 應用SVM的PM2.5未來一小時濃度動態預報模型[J]. 紅外與激光工程,2017, 46(2):252-259.(ZHANG C J, DAI L J, MA L M. Dynamic model for forecasting concentration of PM2.5 one hour in advance using support vector machine[J]. Infrared and Laser Engineering, 2017, 46(2): 252-259.)

[16] ZHANG C J, DAI L J, MA L M. Rolling forecasting model of PM2.5 concentration based on support vector machine and particle swarm optimization[C]// Proceedings of the 2016 International Symposium on Optoelectronic Technology and Application. Bellingham, WA: SPIE, 2016: 10156.

[17] 梁棟, 楊勤英, 黃文江, 等. 基于小波變換與支持向量機回歸的冬小麥葉面積指數估算[J]. 紅外與激光工程，2015, 44(1)：335-340. (LIANG D，YANG Q Y，HUANG W J，et al. Estimation of leaf area index based on wavelet transform and support vector machine regression in winter wheat[J]. Infrared and Laser Engineering, 2015, 44(1):335-340.)

[18] 金焱, 褚政, 張瑾. 改進加權支持向量機回歸方法器件易損性評估[J]. 強激光與粒子束, 2014, 26(12):177-182.(JIN Y，CHU Z，ZHANG J. Improved weighted support vector regression algorithm for vulnerability assessment of electronic devices illuminated or injected by high power microwave [J]. High Power Laser and Particle Beams, 2014, 26(12): 177-182.)

[19] YOU Z Y, CHEN W R, HE G J, et al. Adaptive weight particle swarm optimization algorithm with constriction factor[C]// Proceedings of the 2010 International Conference of Information Science and Management Engineering. Washington, DC: IEEE Computer Society, 2010: 245-248.

This work is partially supported by the National Natural Science Foundation of China (41575046), the Project of Commonweal Technique and Application Research of Zhejiang Province (2016C33010), the Science and Technology Planning Program of Jinhua City (2014- 3- 028).

DAILijie, born in 1990, M. S. candidate. His research interests include signal and information processing, machine learning, pattern recognition.

ZHANGChangjiang, born in 1974, Ph. D., professor. His research interests include signal and information processing, machine learning, pattern recognition.

MALeiming, born in 1975, Ph. D., research fellow. His research interests include meteorological numerical forecasting.

Dynamicforecastingmodelofshort-termPM2.5concentrationbasedonmachinelearning

DAI Lijie1, ZHANG Changjiang1*, MA Leiming2

(1.CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China;2.CentralMeteorologicalObservatory,ShanghaiMeteorologicalBureau,Shanghai200030,China)

The forecasted concentration of PM2.5 forecasting model greatly deviate from the measured concentration. In order to solve this problem, the data (from February 2015 to July 2015), consisting of measured PM2.5 concentration, PM2.5 model (WRF-Chem) forecasted concentration and model forecasted data of 5 main meteorological factors, were provided by Shanghai Pudong Meteorological Bureau. Support Vector Machine (SVM) and Particle Swarm Optimization (PSO) algorithm were combined to build rolling forecasting model of hourly PM2.5 concentration in 24 hours in advance. Meanwhile, the nighttime average concentration, daytime average concentration and daily average concentration during the upcoming day were forecasted by rolling model. Compared with Radical Basis Function Neural Network (RBFNN), Multiple Linear Regression (MLR) and WRF-Chem, the experimental results show that the proposed SVM model improves the forecasting accuracy of PM2.5 concentration one hour in advance (according with the results concluded from finished research), and can comparatively well forecast PM2.5 concentration in 24 hours in advance, and effectively forecast the nighttime average concentration, daytime average concentration and daily average concentration during the upcoming day. In addition, the proposed model has comparatively high forecasting accuracies of hourly PM2.5 concentration in 12 hours in advance and nighttime average concentration during the upcoming day.

machine learning; Particle Swarm Optimization (PSO) algorithm; dynamic model; rolling forecasting

2017- 05- 16;

2017- 06- 09。

國家自然科學基金資助項目(41575046)；浙江省科技廳公益性技術應用研究計劃項目(2016C33010)；浙江省金華市科技計劃項目(2014- 3- 028)。

戴李杰(1990—)，男，浙江桐廬人，碩士研究生，主要研究方向：信號與信息處理、機器學習、模式識別； 張長江(1974—)，男，黑龍江齊齊哈爾人，教授，博士，主要研究方向：信號與信息處理、機器學習、模式識別； 馬雷鳴(1975—)，男，新疆石河子人,研究員，博士，主要研究方向：氣象數值預報。

1001- 9081(2017)11- 3057- 07

10.11772/j.issn.1001- 9081.2017.11.3057

(*通信作者電子郵箱zcj74922@zjnu.edu.cn)

P456.8

A