不同應力路徑下旋轉硬化方程的統一表示及驗證

張浩 吳志鴻 張峰 戴自航

摘 要：在收集到的大量試驗數據的基礎上，結合旋轉硬化表達式，提出一個適用于不同應力路徑下的旋轉硬化表達式，該公式中共有兩個參數，通過理論分析得到這兩個參數的確定方法。將該公式導入修正劍橋模型來模擬土體在不同加載路徑下的應力 應變行為，將模擬結果與試驗結果進行對比，結果顯示，采用該旋轉硬化表達式的各向異性本構模型得到的結果與試驗結果均吻合較好，從而驗證了該旋轉硬化表達式的合理性。

關鍵詞：旋轉硬化;應力路徑;統一表示;本構模型

中圖分類號：TU411

?文獻標志碼：A? 文章編號：1674-4764（2018）06-0039-07

Unified expression and verification of rotational hardening

equations under different stress paths

Zhang Hao1，2 ， Wu Zhihong1， Zhang Feng1， Dai Zihang2

（1.Strait Construction and Development Co.，Ltd， Fuzhou? 350003， P.R.China;

2.College of Civil Engineering， Fuzhou University， Fuzhou? 350116， P.R.China）

Abstract：Based on the collected series of experimental data and many well-known rotational hardening expressions， a rotational hardening expression for different stress paths is proposed， mainly including 2 parameters which can be determined in a direct way through analysis. The proposed rotational hardening expression has been implemented to the MCC model and adopted to represent the stress-strain behavior of? clays under different loading paths. The simulations are compared with the experimental results. The comparisons show that the simulated results with this proposed method have good agreement with the experimental results， verifying the rationality of the proposed rotational hardening expression.

Keywords：rotational hardening; stress path; unified expression; constitutive model

原狀土體是在一定應力條件下形成的，土體顆粒結構產生定向排列，在宏觀結構上形成一定的各向異性。同時，土體的變形與加載應力路徑密切相關，采用不同的應力加載路徑會得到不同的應變，引起初始各向異性的變化，形成土體顆粒之間的新的排列，這種新的各向異性稱為誘發性各向異性。在屈服面模型中，這種各向異性通過屈服面的旋轉來表示，這就是模型中采用的旋轉硬化表達式。

研究人員對旋轉硬化規律采用了不同的表達形式。Wheeler等[1] 提出的旋轉硬化表達式同時考慮了塑性體積應變和塑性剪切應變的影響，但旋轉硬化參數不能直接確定，需要通過反分析，并且沒有考慮洛德角的影響。Whittle等[2] 提出的旋轉硬化表達式采用臨界狀態線作為旋轉的邊界線，只考慮了塑性剪切應變對旋轉硬化的影響，這與試驗現象不吻合。Taiebat等[3] 沒有考慮塑性剪切應變的影響，同時，參數值不能直接確定，需要通過反分析，屈服面的旋轉存在邊界線。Zhang等[4] 依據交變加載試驗結果提出了一個旋轉硬化表達式，該表達式考慮了塑性剪切應變的作用，但是，參數需要通過反分析才能確定，給計算帶來不便。Hashiguchi[5] 認為屈服面旋轉過程中塑性體積應變沒有影響，采用 K ?0線作為屈服面的傾斜線，這與已有的試驗結果不符。Hueckel等[6] 同時考慮了塑性體積應變和塑性剪切應變對旋轉速度的影響，但是，旋轉硬化參數的確定缺乏依據。Newson等[7] 采用應力表示屈服面的旋轉速度，屈服面的旋轉只考慮了每一步的應力增量，沒有考慮剪切應力的作用，同時，由于該本構模型采用非相關聯流動法則，使得該旋轉硬化表達式非常復雜。王立忠等[8] 提出的表達式同時考慮了塑性體積應變和塑性剪切應變的作用，認為屈服面的旋轉存在一定的范圍，超過該范圍時，對應屈服面的傾 斜角度平衡值為0。對土體旋轉硬化規律表達形式方面的研究成果還有很多[9-14] ，目前提出的旋轉硬化表達式均是針對某一種具體的應力路徑所提出的，當應力路徑發生改變時，旋轉硬化表達式的適用性有待驗證。 基于此，在收集到的試驗數據基礎上，提出了一個考慮應力路徑變化的旋轉硬化規律表達式，該表達式包括兩個參數，通過理論分析得到了這兩個參數的直接確定方法。將該規律導入修正劍橋模型，建立了一個能描述各向異性的本構模型，采用該模型模擬了3種不同應力路徑下土體的應力 應變關系，將模擬結果與試驗結果進行對比，證明該旋轉硬化表達式能適用于不同應力路徑。

1 旋轉硬化方程的統一表示

1.1 旋轉硬化方程的分類

研究人員針對旋轉硬化規律采用了不同的表達形式，不同表達形式之間，塑性剪切應變和塑性體積應變對應的平衡值也不相同。依據加載應力比 η 和相對應屈服面的傾斜角度平衡值 α 之間的關系，這些旋轉硬化表達式可劃分為3種類別。

第1種： η 與 α 之間為線性關系，不存在 旋轉極限線，方程式為

α=xη （1）

式中： x 為 η 與 α 之間的線性比例關系參數，其取值一般為1和0，這種關系式比較典型的旋轉硬化規律包括Whittle等[2] 、Taiebat等[3] 及Zhang等[4] 提出的旋轉硬化表達式。

第2種： η 與 α 之間為線性關系，但是存在旋轉極限線，超出旋轉范圍極限線之后，屈服面對應的傾斜角度平衡值 α 為0，表達式為

α=η ?η ≤ M- α? α=0 ?η > M- α?? ??（2）

這種關系式比較典型的旋轉硬化規律包括王立忠等[8] 提出的旋轉硬化表達式。

第3種： η 與 α 之間為曲線關系，比較典型的包括Wheeler等[1] 提出的旋轉硬化規律表達式。

3 3η-4α? M2-η2 =±8β 3α-η? η-α? （3）

為了分析這3種表達方式的合理性，收集了14種數據的應力比 η/M 和與應力比相對應的平衡值 α/M 之間的試驗結果（[1]， [15-17]） ， M 為考慮了洛德角影響的臨界狀態線的斜率，試驗結果與采用這3種表達式進行模擬的結果對比如圖1所示。

從圖1可以看出，在歸一化應力比 η / M 較低的情況下，除了第1種表達式中 x 取0的情況外，依據這3種表達式得到的模擬結果與試驗結果之間都吻合得比較好，當 η/M 的值達到一定值之后，塑性剪切應變的影響程度開始增加，隨著歸一化應力比 η/M 的增加 ，α/M 反而開始下降。采用第2種關系式得到的曲線雖然也能反映出這種趨勢，但是模擬曲線與試驗結果之間存在明顯差距。

1.2 旋轉硬化方程的統一表示及參數確定

1.2.1 旋轉硬化表達式 ?從圖1可以看出，第3種表達式能較好地反映 α/M 隨 η/M 的增加而下降的趨勢，但試驗結果與模擬結果之間存在一定誤差，尤其在拉伸狀態下，這種誤差比較明顯。同時，通過試驗數據也可以看出，在應力比 η 較低的情況下，塑性體積應變占主導位置， η 與 α 之間相等，當應力比 η 趨向于 M 時， α 接近于0。基于此，提出旋轉硬化規律的統一表達式為

d α=μ? aη-α? ?d ε p v ?-β bη-α? ?d ε p s ???（4）

式中總共包含4個參數，分別是 μ 、 ?β 、 ?a 和 b ，當這4個參數取不同的值時，就可以得到不同的旋轉硬化規律表達式。同時，從圖1可以看出，在應力比 η / M 較低時， η/M 近似等于 α/M ，當達到一定程度之后， α/M 隨著 η/M 的增大逐漸減小，最后趨向于0。為了反映這種趨勢，本文提出參數 a 和 b 分別取1和0，得到的旋轉硬化規律表達式為

d α=μ? η-α? ?d ε p v ?+βα ?d ε p s ???（5）

為驗證該旋轉硬化方程的合理性，將該表達式嵌入修正劍橋模型，有關修正劍橋模型的具體介紹可參考文獻[18] 。建立了一個能描述各向異性的彈塑性本構模型，模型的屈服面方程表示為

f= q-αp - M2-α2? p ?c -p p=0 （6）

1.2.2 旋轉硬化表達式參數的確定

旋轉硬化表達式包含兩個參數，分別是 μ 和 β ，這里介紹對這兩個參數的推導過程。若繼續一維壓縮過程，屈服面不發生旋轉，即

d α=μ? η-α? ?d ε p v ?-βα ?d ε p s ??=0 （7）

一維壓縮過程中

d ε p s ??d ε p v ?=? 2 3? ?d ε 1- d ε 3?? ?dε ?1+2 d ε 3? = 2 3? （8）

式中： ?d ε ?1和 ?d ε ?3分別表示壓縮過程中的單元體豎向應變和水平應變，聯合式（7）和式（8），得到

β= 3 η K 0 -α K 0 ??2α K 0 ???（9）

結合方程式（6），一維壓縮中塑性體積應變和塑性剪切應變之間的關系表示為

d ε p s ??d ε p v ??= ??? f ? q?? ? f ? p? ?= ?2（η K 0 ???-α K 0 ???） M2-η K2 0 ?????= ?2 3? （10）

得到

α K 0 ????= ?η K2 0 ????+ 3η K 0 ???-M2 3? （11）

將式（11）代入式（9），可得到

β= 3 η K 0 -α K 0 ??2α K 0 ?= 3 M2-η2 K 0 ??2 η2 K 0 +3η K 0 -M2?? （12）

如果將土體式樣各向同性固結到先期壓力的2～ 3倍左右，則土體的各向異性將基本消失[19] ，此時，發生的塑性體積應變可表示為

ε p v = λ-k 1+e 0 ?ln ??p p 0? = λ-k 1+e 0 ?ln ?2～3 ≈ λ-k 1+e 0? （13）

各向同性固結時，應力比 η =0， 塑性剪切應變和塑性體積應變之間的比例關系可表示為

d ε p s ??d ε p v ?=? ? f ? q?? ? f ? p? = 2（η-α） M2-η2 = -2α M2? （14）

將式（14）代入式（5），得

1 α 2αβ-M2? ?d α= μ M2 ?d ε p v ?（15）

對式（15）左邊積分，得

∫α α 0 ?1 α 2αβ-M2? ?d α=? 2β M2? ?ln ?2αβ-M2 2αβ?? α α 0 ?（16）

假定屈服面累計旋轉到初始值 α ?0的0.1倍時，土體顯示各向同性性質，這樣聯合式（13）、式（15）和式（16）就可求出參數 μ 的表達式。

μ= 2β 1+e 0? λ-κ ?ln ?10M2-2α 0β M2-2α 0β? （17）

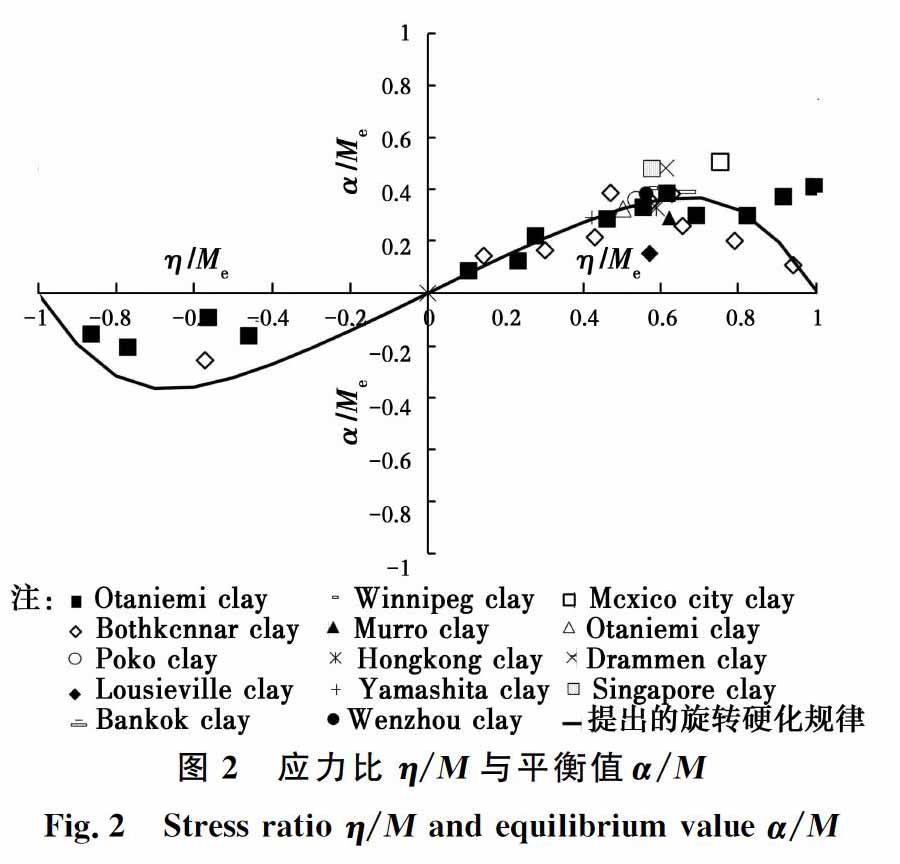
聯合式（5）、式（12）和式（17），可建立 α/M 和 η/M 之間的關系曲線，如圖2所示。

從圖2可以看出，采用本文提出的旋轉硬化表達式得到的曲線與試驗結果之間吻合得較好，能很好地反映屈服面的傾斜角度先增后減，最后趨向于0的過程。將提出的旋轉硬化表達式導入修正劍橋模型，模擬屈服面的旋轉以及不同應力路徑下的土體試樣的應力 應變行為，模型需要輸入的模型與修正劍橋模型需要輸入的參數相同，總共包含6個，分別為 e 0 、 λ 、 κ 、 ?M 、 υ ?和 p m0 ， 參數的物理意義可參考文獻[18] 。

2 不同應力路徑試驗的模擬

為了分析旋轉硬化對不同加載路徑下土體應力 應變關系的影響，選擇3種不同的應力路徑進行分析，分別是溫州軟土三軸排水試驗[20] 、BBC（Boston Blue Clay）土的三軸不排水試驗[21] 、Otaniemi土的循環加載試驗[22] ，這3種土需要輸入模型的參數見表1。

2.1 三軸排水試驗

沈愷倫[20] 對溫州軟土進行了三軸排水試驗，試驗過程先依照原狀土的應力狀態進行固結，然后再分別進行排水狀態下的三軸壓縮試驗。圖3和圖4表示的是應力路徑為BCD50和BED33時，三軸壓縮試驗結果和采用不同旋轉硬化表達式得到的模擬結果之間的對比。

圖3是應力路徑為BCD50時試驗結果和采用不同旋轉硬化表達式時得到的模擬結果之間的對比，從圖中可以看出，總體上模擬結果與試驗結果之間吻合得比較好，采用不同旋轉硬化表達式得到的模擬曲線之間非常接近，在模擬 p - ε ?v時，隨著體積應變的發展，模擬曲線之間開始出現差距。當體積應變達到3%時，模擬曲線之間開始出現一定的差距，與試驗結果之間的差距也慢慢增大，在模擬 q - ε ?s時，采用不同旋轉硬化表達式得到的模擬結果與試驗結果之間非常接近，都能較準確地模擬 q - ε ?s的發展趨勢。

圖4是三軸拉伸試驗BED-33時試驗結果與模擬結果之間的對比，從圖中可以看出，在模擬 p - ε ?v曲線時，采用不同旋轉硬化表達式對模擬結果的影響不是很明顯，采用4種旋轉硬化表達式得到的模擬曲線之間非常接近，都能較準確地模擬 p - ε ?v之間的發展趨勢，但在模擬 q - ε ?s曲線時，模擬結果與試驗結果存在一定的誤差，當剪切應變較小時，模擬曲線之間比較接近，隨著剪切應變的發展，模擬曲線之間開始出現一定程度的誤差，采用本文提出的旋轉硬化表達式得到的模擬結果與試驗結果之間吻合較好。

2.2 三軸不排水試驗

Ladd等[21] 對BBC（Bonston Blue Clay）土進行了三軸不排水壓縮試驗，所取土試樣首先各向同性固結到150 kPa， 然后根據不同的超固結比值 R ?oc ?，分別卸載到相應的應力值，這里選取的 R oc 分別為1和4，土樣在整個加載過程中保持不排水條件，需要輸入模型的土體參數見表1。Yu等[23] 也對該試驗進行了數值研究。

圖5為模擬結果與試驗結果之間的對比，從圖中可以看出，在對應力路徑 p - q 進行模擬時，采用不同旋轉硬化表達式得到的模擬曲線與試驗曲線之間比較接近，采用這4種旋轉硬化表達式都能較準確地反映出 p - q 之間的變化趨勢。在模擬 q - ε ?s時，當OCR為1，即當試樣為正常固結時，模擬曲線位于試驗曲線的上部，在出現相同的剪切應變 ε ?s時，模擬得到的剪切應力 q 要大于試驗過程中的剪切應力，同時，采用不同旋轉硬化表達式得到的模擬曲線之間也不是非常接近，相比較而言，采用本文提出的旋轉硬化表達式得到的模擬曲線與試驗曲線之間最為接近。當OCR為4時，在模擬應力路徑 p - q 時，不同旋轉硬化表達式得到的模擬結果與試驗結果之間非常接近，都能準確地反映出應力路徑 p - q 的變化趨勢，在模擬 q - ε ?s時，模擬結果與試驗結果之間存在一定的誤差，但這種誤差要小于OCR為1時試驗結果與模擬結果之間的誤差，總體而言，這4個旋轉硬化表達式都能較準確地反映出變形趨勢，采用本文提出的旋轉硬化表達式得到的模擬結果與試驗結果之間最為接近。

2.3 循環加載試驗

循環加載試驗選取Otaniemi重塑土進行了研究，這種土的相關參數及試驗過程見Karstunen等[22] 的研究成果，在三軸壓縮之前，先將試樣按照一定的應力路徑 η ?0進行固結，隨后將試樣進行卸載到一定值， 然后對試樣進行加載卸載循環試驗。本文選取了兩組試樣，分別是試樣CAE3516R和試樣CAE3519R，試樣CAE3516R模擬結果如圖6所示。

從圖6可以看出，對于CAE3516R試樣，在模擬應力 應變曲線 p - ε ?v時，采用不同旋轉硬化表達式對模擬結果有較大影響。初始加載時，采用Whittle等和王立忠等提出的旋轉硬化表達式得到的模擬曲線位于試驗曲線的上部，采用本文提出的旋轉硬化表達式與Hueckel等提出的旋轉硬化表達式得到的模擬曲線之間比較接近。卸載階段，不同旋轉硬化表達式得到的模擬結果之間的差距比加載階段不同旋轉硬化表達式得到的模擬結果之間的差距要明顯一些，相比較而言，采用本文提出的旋轉硬化表達式得到的模擬結果與試驗結果之間更為接近。在模擬應力 應變關系 q - ε ?s時， 采用4種旋轉硬化表達式都能反映出應力 應變關系的變化趨勢，但是，相比較應力 應變關系 p - ε ?v而言，不同旋轉硬化表達式得到的模擬曲線之間的差距更明顯。

圖7為CAE3519R的試驗結果與模擬結果之間的對比，從圖中可以看出，在模擬應力 應變曲線 p - ε ?v時，加載階段，不同旋轉硬化表達式得到的模擬結果之間存在一定差距，卸載階段，不同模擬結果之間則比較吻合。在模擬應力 應變關系 q - ε ?s時，不同旋轉硬化表達式得到的模擬曲線之間差距比較明顯，采用本文提出的旋轉硬化表達式得到的模擬曲線與實測數據之間最為接近。

3 結論

對提出的旋轉硬化規律表達式進行總結，依據加載應力比 η 和相對應屈服面的傾斜角度平衡值 α 之間的關系，將提出的旋轉硬化表達式劃分為3種類型，分別是線性關系同時不存在旋轉極限線、線性關系同時存在旋轉極限線以及曲線關系。建立了這3種關系式的函數曲線，函數曲線與試驗結果之間的對比結果顯示，采用曲線表達形式與試驗結果之間最為吻合。

在采用曲線型表達方程的基礎上，提出了一個適用于不同應力路徑下的旋轉硬化表達式，同時考慮了塑性體積應變和塑性剪切應變對旋轉速度的影響。表達式共包含兩個參數，通過理論分析，得到這兩個參數的確定方法。將所提出的旋轉硬化表達式導入修正劍橋模型，建立一個能描述各向異性的本構模型，采用此模型模擬了不同應力路徑下的應力 應變關系，模擬過程中，同時采用了其他3種旋轉硬化表達式。將試驗結果與模擬結果之間以及采用不同旋轉硬化表達式得到的模擬結果之間進行對比分析，分析結果驗證了提出的旋轉硬化表達式的合理性。

參考文獻：

[1] ??WHEELER ?S J， NAATANEN A， KARSTUNEN M， et al. An anisotropic elastoplastic model for soft clay [J]. Canadian Geotechnical Journal， 2003， 40（2）：403-418.

[2] ?WHITTLE ?A J， KAVVADAS M J. Formulation of MIT-E3 constitutive model for overconsolidated clays [J]. Journal of Geotechnical Engineering， 1994， 120（1）：173-198.

[3] ?TAIEBAT ?M， DAFALIAS Y F. Simple anisotropic sand plasticity model [J]. International Journal of Numerical and Analytical Methods in Geomechanics， 2008， 32（8）：915-948.

[4] ?ZHANG ?F， YE B， NODA T， et al. Explanation of cyclic mobility of soils approach by stress-induced anisotropy [J]. Soils and Foundations， 2007， 47（4）：635-648.

[5] ??HASHIGUCHI ?K. Elastoplastic constitutive equation of soils with the subloading surface and the rotational hardening [J]. International Journal for Numerical and Analytical Methods in Geomechanics， 1998， 12（8）：197-227.

[6] ?HUECKEL ?T， TUTUMLUER E. Modeling of elastic anisotropy due to one-dimensional plastic consolidation of clays [J]. Computers and Geotechnics， 1994， 16（4）：311-349.

[7] ?NEWSON ?T A， DAVIES C R. A rotational hardening constitutive model for anisotropically consolidated clay [J]. Soils and Foundations， 1996， 36（3）：13-20.

[8] ??王立忠， 沈愷倫. ?K ?0固結結構性軟黏土的旋轉硬化規律研究[J].巖土工程學報， 2008， 30（6）：863-872.

WANG L Z， SHEN K L. Rotational hardening law of ?K ?0 consolidated structured soft clays [J].Chinese Journal of Geotechnical Engineering， 2008， 30（6）：863-872. （in Chinese）

[9] ?YIN ?Z Y， YIN J H， HUANG H W.Rate-dependent and long-term yield stress and strength of soft Wenzhou marine clay： experiments and modeling [J]. Marine Georesources and Geotechnology， 2015， 33（1）：79-91.

[10] ?YIN ?Z Y， WANG J H. A one-dimensional strain-rate based model for soft structured clays [J]. Science in China Series， 2012， 55（1）：90-100.

[11] ??姚仰平， 張丙印， 朱俊高. 土的基本特性、本構關系及數值模擬研究綜述[J]. 土木工程學報，2012， 45（3）：128-150.

YAO Y P， ZHANG B Y， ZHU J G. Behaviors， constitutive models and numerical simulation of soils [J].China Civil Engineeing Journal， 2012， 45（3）：128-150. （in Chinese）

[12] ??楊召煥， 王建華.循環荷載作用下飽和軟土的各向異性邊界面模型[J].巖土力學，2016， 31（Sup1）：63-70.

YANG Z H， WANG J H. Anisotropic bounding surface model for saturated soft clay under cyclic loading [J]. Rock and Soil Mechanics， 2016， 31（Sup1）：63-70. （in Chinese）

[13] ??褚福永， 朱俊高， 趙顏輝， 等. 粗粒土初始各向異性彈塑性模型[J].中南大學學報，2012，43（5）：1914-1919.

ZHU F Y， ZHU J G， ZHAO Y H， et al. An elastoplastic model for granular soil considering initial anisotropy [J]. Journal of Central South University， 2012， 43（5）：1914-1919. （in Chinese）

[14] ??劉正義.軟黏土屈服特性及各向異性屈服面方程研究[D]. 杭州： 浙江大學，2014.

LIU Z Y. Research on the yield behavior and anisotropic yield surface equation of soft clay [D]. Hangzhou： Zhejiang University， 2014. （in Chinese）

[15] ?KEVIN ?M. The stress-strain behavior of bothkennar clay [D]. Glasgow： University of Glasgow， 2006.

[16] ??但漢波，王立忠.基于彈黏塑性本構模型的旋轉硬化規律[J]. 巖石力學與工程學報， 2010， 29（1）：184-192.

DAN H B， WANG L Z. Rotational hardening law based on elastoviscoplastic constitutive model [J]. Chinese Journal of Rock Mechanics and Engineering， 2010， 29（1）：184-192. （in Chinese）

[17] ??但漢波. 天然軟粘土的流變特性[D]. 杭州： 浙江大學，2009.

DAN H B. Time dependent behavior of natural soft clays [D]. Hangzhou： Zhejiang University， 2009. （in Chinese）

[18] ?ROSCOE ?K H， BURLAND J B. On generalized stress strain behavior of wet clay in engineering plasticity [M]. London： Cambridge University Press， 1968.

[19] ?ANANDARAJAH ?A， KUGANENTHIRA N， ZHAO D.Variation of fabric anisotropy of kaolinite in triaxial loading [J]. Journal of Geotechnical Engineering， 1996， 122（8）：633-640.

[20] ??沈愷倫. 軟粘土結構性、塑性各向異性及其演化[D]. 杭州： 浙江大學， 2006.

SHEN K L. Degradation of soil structure and anisotropic plasticity evolution of natural clay [D]. Hangzhou： Zhejiang University， 2006.（in Chinese）

[21] ?LADD ?C C， VARALLYAY J. The influence of the stress system on the behavior of saturated clays during undrained shear [R]. Research Rep. No. R65-11， Department of Civil Engineering， MIT， Cambridge， MA， 1965.

[22] ?KARSTUNEN ?M， KOSKINEN M. Plastic anisotropy of soft reconstituted clays [J]. Canadian Geotechnical Journal， 2008， 45（3）： 314-328.

[23] ?YU ?C， XU Q， YIN Z Y. Softening response under undrained compression following anisotropic consolidation [J]. Journal of Central South University， 2013， 20（6）：1703-1712.