單軸應變對H在α-Fe中占位及擴散的影響

李守英 王勇趙衛民

1)(中國石油大學(華東)機電工程學院,青島 266580)

2)(青島濱海學院機電工程學院,青島 266555)

單軸應變對H在α-Fe中占位及擴散的影響

李守英1)2)王勇1)趙衛民1)?

1)(中國石油大學(華東)機電工程學院,青島 266580)

2)(青島濱海學院機電工程學院,青島 266555)

金屬Fe,間隙H原子,第一性原理,應力誘導擴散

1 引 言

近年來,環境保護、能源枯竭成為世界各國共同關注的重要問題.氫在燃燒或氧化后的產物是液態水或水蒸氣,作為一種潔凈的可再生能源,由于來源廣泛、轉化效率高,被視為21世紀最具有發展潛力的清潔能源[1?4].對于氫的大量、長距離氣態輸送,管道是最高效、低成本的方式.管道輸氫中一個很重要的安全問題是氫脆.管線鋼長期暴露在高壓氫氣中,其強度會大大降低,導致氫脆失效.特別是管線鋼的焊接接頭區域,由于焊接熱輸入,使得接頭局部出現焊接殘余應力、焊接缺欠等問題,改變了管道內表面的應力狀態,增加了氫致失效的危險[5?7].應力誘導氫脆的機制至今尚無統一定論[8].為了研究應力誘導氫脆問題,需要弄清應力作用下H原子與金屬Fe的相互作用.

關于無應力作用下H原子與Fe的相互作用已有較多的理論研究.Sanchez[9]應用第一性原理CASTEP計算結果表明H原子濃度較低時,H優先占據四面體間隙(Ts),濃度較高時H優先占據八面體間隙(Os).Gong等[10]應用基于簇模型的自旋極化方法計算結果表明H以0.11 eV的優勢優先占據Os.Lee和Jang[11]采用嵌入原子理論研究了Fe-H體系的間隙原子勢,發現H原子優先占據α-Fe的Ts位.Sorescu[12]應用密度泛函理論,通過計算溶解能認為H在α-Fe中的穩定位置是Ts位,H原子與鄰近的4個Fe原子之間的距離是1.667 ?,并沒有結合態密度、電荷布居以及差分電荷密度從電子層次對H與α-Fe晶格的相互作用進行分析.關于H在應力α-Fe中的溶解位置以及應力作用下α-Fe電子結構的變化未見報道.本文采用密度泛函理論,從電子結構層次分析了H原子與應變α-Fe的相互作用及應變對H原子擴散的影響.

2 計算方法與計算模型

本文計算采用CASTEP模塊、周期性邊界條件,晶體波函數采用超軟贗勢和平面波基組展開,選用以廣義梯度近似修正的Perdew-Burke-Ernzerhof泛函描述電子間交換關聯能,選取平面波截斷能為425 eV,自洽場循環收斂1.0×10?5eV/atom,力收斂為0.03 eV/atom.k點取樣采用Monkhorst-Pack網格,k點取值根據不同超胞體系進行設置.體相α-Fe優化取19×19×19,含氫原子的超胞體系則根據超胞的大小而不同.H原子的優化計算,將其放入12 ?×12 ?×12 ?的立方盒子中,k點取1×1×1.文中所選參數均進行了收斂性測試.α-Fe屬于體心立方結構,優化后的晶格常數a=2.845 ?,與試驗結果2.866 ?基本一致,誤差為0.7%.

H的間隙占位以及擴散計算采用α-Fe的2×1×1超胞結構,H原子在α-Fe晶胞中的間隙位置分別位于Ts,Os,如圖1所示.

應力的引入是通過在應力方向施加一單軸拉伸應變ε[13].先對Ts和Os位的Fe4H進行結構優化,使得模型晶胞尺寸和原子處于最穩定位置.基于優化好的模型在[100]方向對其進行單向拉伸,通過改變模型在該方向的尺寸來實現,應變ε在?5%—5%之間.

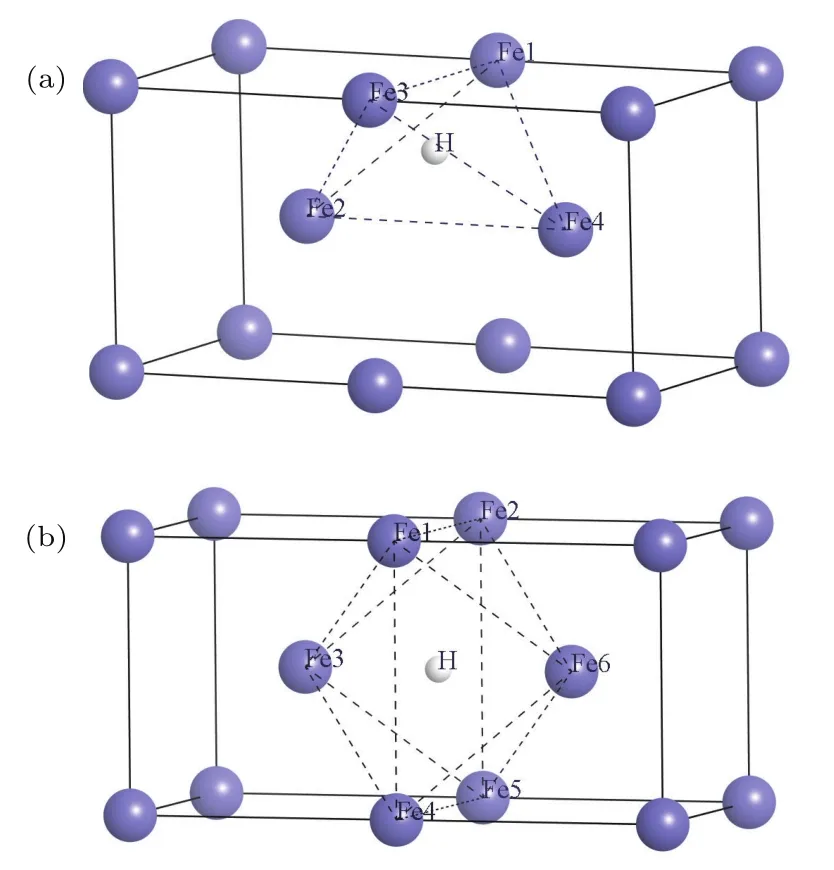
圖1 (網刊彩色)(a)Ts位和(b)Os位的2×1×1 α-Fe超胞Fig.1.(color online)(a)The tetrahedral interstice(Ts)and(b)octaedral interstice site(Os)in 2×1×1 α-Fe supercell.

3 計算結果與討論

3.1 H原子在應變α-Fe中的溶解能

H原子在α-Fe晶胞中有兩個可能的間隙位置,分別為Ts和Os.為分析不同應變下H在α-Fe中的優先占據位,計算了H原子在α-Fe中Ts和Os位的溶解能.溶解能描述間隙H原子和不同應變體系α-Fe原子的相互作用[14?16],定義為

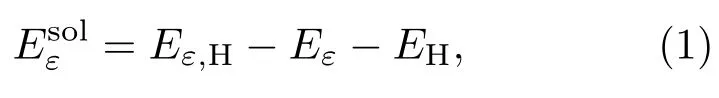
其中,Eε,H,Eε分別是含H、不含H的應變α-Fe晶胞的能量,EH是一個H原子的能量.從定義式可以看出,溶解能為負值時,溶解過程為放熱反應,H原子易溶解于金屬中.溶解能數值為負且越小時,H原子越易溶于α-Fe;溶解能數值為正且越大時,H原子越難溶入,該Fe-H體系結構越不穩定.不同應變和不同占位的溶解能如圖2所示,可以看出,無應變時,在Ts和Os位溶解能均為正值與Sichone[17]的計算結果一致;在壓應變及小的拉應變情況下,溶解能也為正值,表明H原子溶解進入α-Fe的Ts和Os需要吸收熱量.

隨著壓應變的減小或拉應變的增加,溶解能逐漸降低,H原子越易溶入α-Fe晶胞.壓應變使得Ts,Os體積減小,H原子難以溶入.拉應變的增大使得晶胞間隙體積增大[18,19],H原子易溶入.所有計算應變情況下,Ts位的溶解能均小于Os位的溶解能.表明單向拉或壓應變情況下,H原子優先占據α-Fe的Ts.

恒定應力下,平衡氫濃度[20]如(2)式所示,可以看出隨著應力的增加,拉應力作用下的平衡氫濃度升高,壓應力作用時,平衡氫濃度降低.

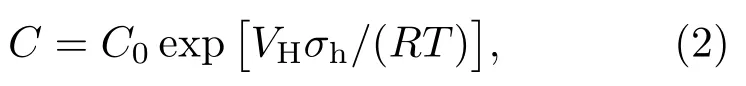
式中,C是應力為σh時的氫濃度;C0是應力為σh=0時的氫濃度;VH是氫的偏摩爾體積,VH=2.0 cm3/mol;σh為靜水應力.這可能是由于應力狀態改變了H原子的溶解能,影響氫的平衡濃度.拉應力作用下,H原子更易溶解,平衡氫濃度高,易向高拉應力區富集.

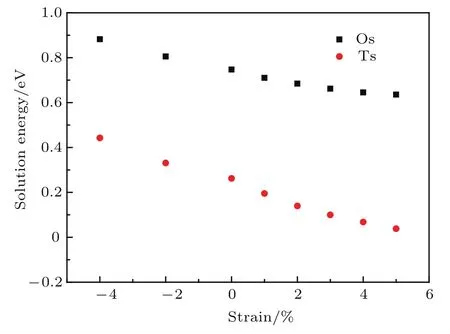
圖2 不同應變Ts和Os位的溶解能Fig.2.Solution energy of hydrogen at Ts and Os under different strain.

3.2 H原子在應變α-Fe晶胞的態密度分析

費米能級處的電子數與晶體的穩定性有關,費米能級處電子數越少,晶體結構越穩定[21].計算得到的費米能級處態密度值列入表1.

表1 不同應變費米能級處態密度Table 1.Density of states at the Fermi level under different strain.

由表1中的費米能級處態密度可以看出,無應力、拉應力、壓應力三種情況下,H位于Ts費米能級處的值低于H位于Os的值,表明H位于Ts的穩定性高于H位于Os.所以不論何種單向應力狀態,H位于Ts更穩定,與之前通過溶解能的分析結果一致.

前面的分析結果表明H原子優先占據α-Fe的Ts,進一步分析Ts位ε=0%的分波態密度,如圖3所示.從圖3可以看出,Fe的4s電子與H的1s電子均在?9.8—?8.5 eV之間有明顯的波峰重合,這表明Fe原子與H原子存在共軛雜化作用.

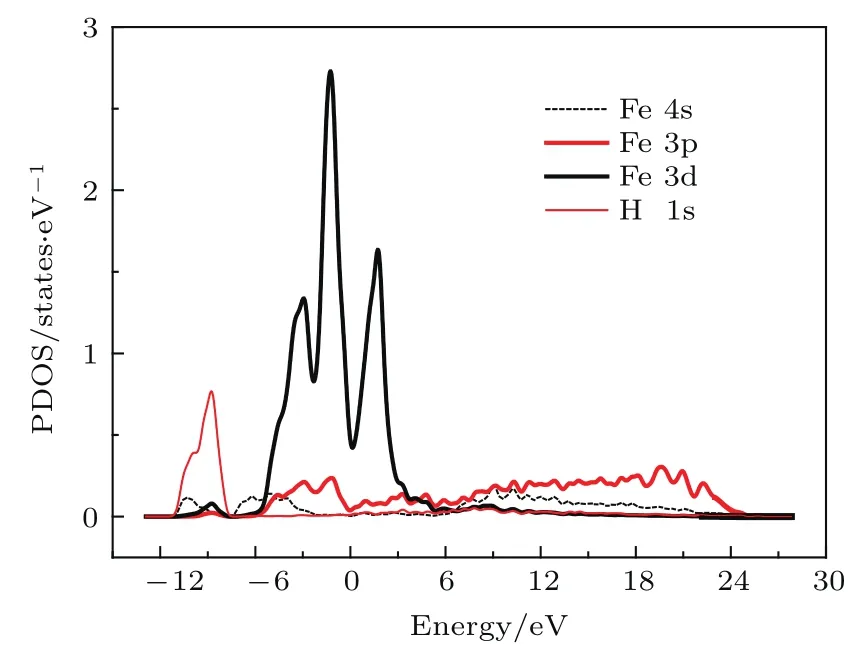
圖3 (網刊彩色)Ts位ε=0%的分波態密度圖Fig.3.(color online)Partial density of states(PDOS)of H at Ts under 0%strain.

3.3 應變對Ts位α-Fe晶體電子結構的影響

為分析不同應變下固溶H原子對α-Fe電荷分布的影響,計算了不同應變下H在Ts位(001)面的差分電荷密度圖,如圖4所示.其中紅色代表得電子,藍色代表失電子.從圖4可以看出,固溶H原子使得電荷重新分布,H原子呈紅色,而鄰近Fe原子呈藍色,表明間隙H原子從近鄰Fe原子得到電子,與張鳳春等[22]和Li等[23]的研究結論一致.壓應變使H原子紅色更深、Fe以及H原子間距減小、電荷轉移增強.拉應變使H原子紅色變淺、Fe以及H原子間距增大、電荷轉移減少.

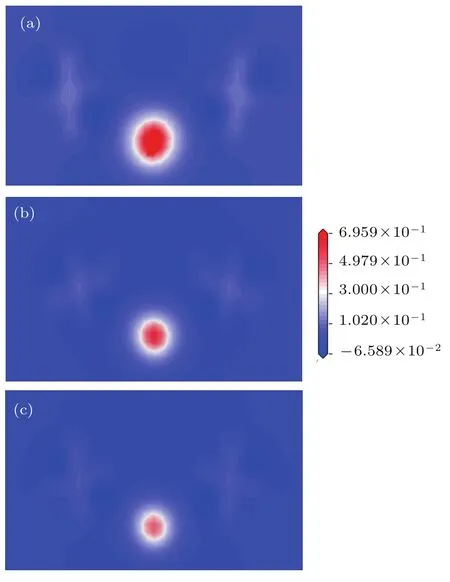
圖4 不同應變Ts位的差分電荷密度圖 (a)ε=?5%;(b)ε=0;(c)ε=5%Fig.4.Charge density difference at Ts under different strain:(a)ε=?5%;(b)ε=0;(c)ε=5%.

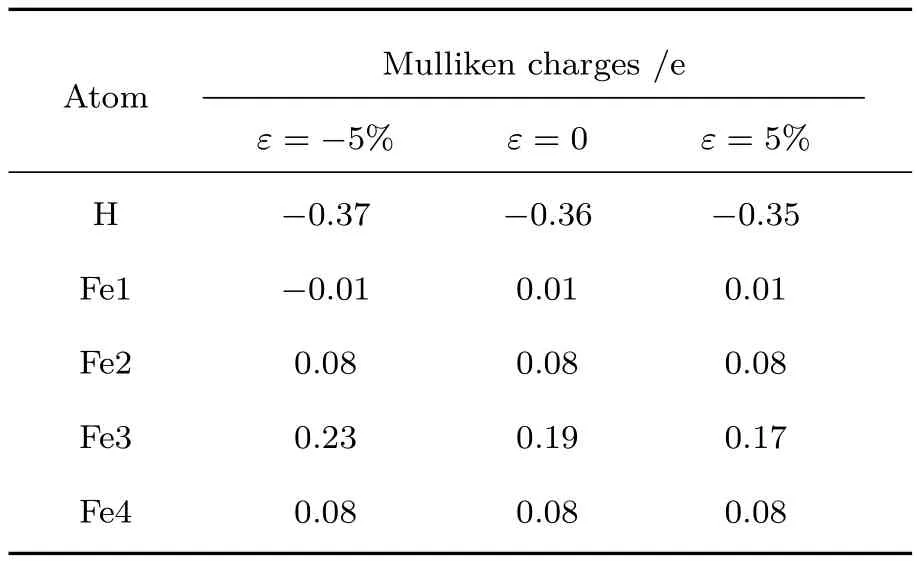
表2 不同應變Ts位Mulliken凈電荷Table 2.Mulliken charge at Ts under different strain.

為了更清楚地理解Fe及H之間的成鍵和電荷轉移,本文對比討論了不同應變Ts位α-Fe-H晶體原子軌道的凈電荷布居.H原子優先占據Ts,僅與臨近的四個Fe原子存在相互作用.從表2中數據可以看出,H從臨近的Fe原子獲取電荷帶負電,Fe原子失去電子帶正電,且壓應變使得電荷轉移增加,拉應變使得電荷轉移減少,與差分電荷密度分析結果一致.

3.4 應變對H在α-Fe中擴散的影響

應變與擴散激活能之間有密切的關系,其中著名的是Flynn[24]原子遷移動力學理論.該理論認為應變體系下的原子的擴散激活能Q與材料的彈性常數C、原子的遷移距離l和彈性應變ε之間有一定關系.Flynn使用二維層模型和試驗參數,沒有考慮原子的弛豫,僅僅是考慮了應力對原子間距的影響[25,26].LST/QST(linear synchronous transit/quadratic synchronous transit)過渡態搜索方法計算的擴散激活能不需要力學試驗數據,完全從第一性原理出發,計算數據更為準確.

本文應用第一性原理LST/QST過渡態搜索的方法計算了H的擴散遷移過程.不同應變作用下,H在α-Fe中穩定的間隙位置是Ts位置,因此主要研究H在與應變垂直的方向[010]兩個Ts位置之間的擴散.不同應變作用下,H原子擴散路徑及相應路徑的能量曲線如圖5所示.擴散路徑中能量最高點與起始點的能量差值為擴散激活能.擴散路徑中能量最高點是擴散的過渡態.從圖5可以看出,擴散過程中α-Fe晶胞的總能量先升高,到達擴散路徑的中點達到最大值后降低.不同應變作用下,H原子擴散的過渡態都是H原子位于Os位.

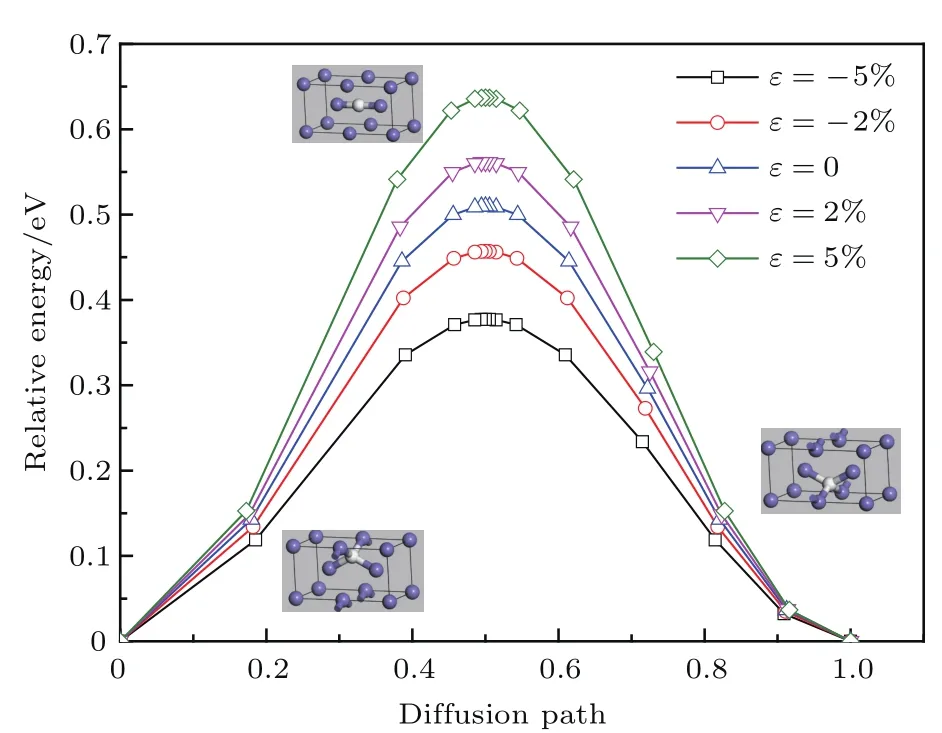
圖5 (網刊彩色)不同應變下H在α-Fe中擴散路徑的能量曲線Fig.5.(color online)The diffusion energy pro file of H atom in a Fe under different strain.

圖6是擴散激活能與應變之間的關系.無應力狀態下H的擴散激活能為0.508 eV.通過圖6可以看出,應變與擴散激活能近似呈線性關系,Q=0.508+2.6ε.擴散激活能與初態Ts能量、過渡態Os能量有關.隨著拉應變的增加,擴散激活能升高,擴散困難;隨著壓應變的增加,擴散激活能降低,擴散更容易.

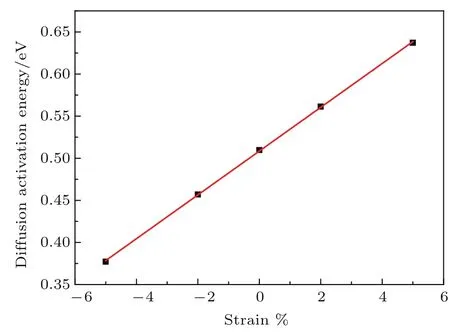
圖6 不同應變作用下的擴散激活能Fig.6.Diffusion activation energy as a function of applied strain.

4 結 論

1)通過溶解能以及費米能級處的態密度計算結果表明在?5%—5%單軸應變α-Fe中,H原子優先占據Ts位,且隨著壓應變減小、拉應變增加,H原子越易溶于α-Fe.

2)差分電荷分析結果表明應變改變了電荷的分布,壓應變使得Ts位的H獲得更多的電子,而拉應變減少了這種電荷轉移.

3)過渡態搜索計算擴散結果表明,在垂直于應變方向,應變與擴散激活能近似呈線性關系,Q=0.508+2.6ε.隨著拉應變的增加,擴散激活能升高,擴散困難;隨著壓應變的增加,擴散激活能降低,擴散更容易.

感謝英國曼徹斯特大學呂建仁教授提供軟件支持.

[1]Zhao Y Z,Meng B 2015Chem.Ind.Eng.Prog.34 3248(in Chinese)[趙永志,蒙波 2015化工進展34 3248]

[2]Dodds P E,McDowall W 2013Energy Policy60 305

[3]Nanninga N,Slifka A,Levy Y 2010J.Res.Natl.Inst.Stan.115 437

[4]Dodds P E,Demoullin S 2013Int.J.Hydrogen Energy38 7189

[5]Jothi S,Croft T N,Wright L 2015Int.J.Hydrogen.Energy40 15105

[6]Briottet T,Batisse R,Dinechin G D 2012Int.J.Hydrogen Energy37 9423

[7]Han Y D,Jing H Y,Xu L Y 2012Mater.Chem.Phys.132 216

[8]Nanninga N,Grochowsi J,Heldt L 2010Corros.Sci.52 1237

[9]Sánchez 2008Phys.Rev.B78 014113

[10]Gong X G,Zeng Z,Zheng Q Q 1989J.Phys.Condens.Matter1 7577

[11]Lee B J,Jang J W 2007Acta Mater.55 6779

[12]Sorescu D C 2005Catal.Today105 44

[13]Dong N,Zhang C,Liu H,Li J,Wu X 2014Comp.Mater.Sci.90 137

[14]Wen P,Li C F,Zhao Y,Zhang F C,Tong L H 2014Acta Phys.Sin.63 197101(in Chinese)[文平,李春福,趙毅,張鳳春,童麗華2014物理學報63 197101]

[15]Jiang D E,Carter E A 2004Phys.Rev.B70 064102

[16]Counts W,Wolverton C,Gibala R 2011Acta Mater.59 5812

[17]Sichone 2014M.S.Thesis(Harbin:Harbin Institute of Technology)

[18]Zhao W M,Zhang T M,Sun J B 2016Electrochim.Acta214 336

[19]Mouanga M,Ber?ot P,Takadoum J 2010Corros.Sci.52 2010

[20]Wang Y F 2014J.Shanghai.Jiaotong Univ.48 610(in Chinese)[王燕飛2014上海交通大學學報48 610]

[21]Kecik D,Aydinol M K 2009Surf.Sci.603 304

[22]Zhang F C,Li C F,Wen P,Luo Q,Ran Z L 2014Acta Phys.Sin.63 227101(in Chinese)[張鳳春,李春福,文平,羅強,冉曾令2014物理學報63 227101]

[23]Li X,Gao C,Xiong X L 2015Int.J.Hydrogen Energy40 10340

[24]Flynn C P 1972Point Defects and Diffusion(London:Oxford University)pp25–30

[25]Zang B,Yi D Q 2013J.Cent.South.Univ.T.44 2214(in Chinese)[臧冰,易丹青2013中南大學學報44 2214]

[26]Li J,Zhen Z Q,Chen D Q,Li S C,Yin S G 2005Rare Metal29 539(in Chinese)[李劍,鄭子樵,陳大欽,李世晨,殷順高2005稀有金屬29 539]

In fluence of single axis strain on site occupation and diffusion of hydrogen atom in α-Fe

Li Shou-Ying1)2)Wang Yong1)Zhao Wei-Min1)?

1)(College of Mechanical and Electrical Engineering,China University of Petroleum(East China),Qingdao 266580,China)
2)(Qingdao Binhai College,Qingdao 266555,China)

16 March 2017;revised manuscript

29 April 2017)

As is well known,hydrogen plays an important role in degrading mechanical properties of steel due to hydrogen embrittlement behavior.Thus,much attention should be paid to the interaction between hydrogen atom and Fe matrix especially in theoretical calculation and mechanism study.In this paper,the site occupations of hydrogen atom under different single axis strains in interstitial of α-Fe atoms are studied by the first principles calculation based on the spin-polarized density functional theory.The Kohn-Sham equations are solved under periodic boundary conditions,by using revised Perdew-Burke-Ernzerhof version of the generalized gradient approximation to account for the electron exchange and correlation.The total energy of the steady state crystal,binding energy,solution energy,density of states,charge density difference and charge population are calculated.The analyses of solution energy and density of states indicate that the hydrogen atom preferentially occupies the tetrahedral interstitial of α-Fe atoms under different single axis strains.With increasing tensile strain or reducing compressive strain,hydrogen atom prefers to occupy the site of tetrahedral interstitial.The analyses of charge population and charge density difference reveal that the hydrogen atom collects charges from Fe atoms,leading to electron density redistribution.The tensile strain reduces the charge transfer slightly while the compressive stress promotes the transfer process.The LST/QST(linear synchronous transit/quadratic synchronous transit)transition state search method is used to investigate the diffusion of hydrogen atom between two tetrahedral interstitials along the direction perpendicular to strain.Diffusion of hydrogen atom goes through transition state where the hydrogen atom is coordinated at octahedral interstitial.The minimum energy pathway for hydrogen diffusion under strainless state indicates the diffusion activation energy with a value of 0.58 eV.It is noticeable that the diffusion activation energy and the strain conforms to linear relation and are consistent with the fitting formula,Q=0.508+2.6ε.The diffusion activation energy increases with reducing compressive strain or increasing tensile strain.According to the calculation process and analysis results,we introduce the interaction between hydrogen atom and α-Fe at a level of electronic structure systematically and figure out the diffusion of hydrogen in fluenced by different states of stress.

metal Fe,interstitials hydrogen, first principles,stress-assisted diffusion

PACS:71.15.Mb,68.43.–h,73.20.HbDOI:10.7498/aps.66.187101

?Corresponding author.E-mail:zhaowm@upc.edu.cn

(2017年3月16日收到;2017年4月29日收到修改稿)

采用基于密度泛函理論的第一性原理方法,研究了H在不同單軸應變下α-Fe中的間隙占位,計算了H原子的溶解能、態密度、電荷差分密度和電荷布居.結果表明:不同單軸拉壓應變作用下,H原子優先占據四面體間隙(Ts)位,且隨著壓應變減小、拉應變增加,H原子越易溶于α-Fe.壓應變使得Ts位的H獲得更多的電子,而拉應變減少了這種電荷轉移.應用LST/QST過渡態搜索計算垂直應變方向的擴散.八面體間隙位是鄰近Ts位H的擴散過渡態.擴散激活能與應變呈線性關系,且隨著壓應變的增加,擴散激活能降低,擴散更容易.

10.7498/aps.66.187101

?通信作者.E-mail:zhaowm@upc.edu.cn