多品種混流生產計劃制定方法研究

（中國計量大學 質量與安全工程學院，杭州 310018）

在激烈的市場競爭環境下，嚴格按質、按量、按期交貨，全方位滿足客戶的要求，己成為企業贏得客戶訂單的重要條件[1]。顧客對產品多樣性的需求呈持續增長趨勢，因此造成產品的生命周期不斷縮短、每批訂單的產品數量不斷變化。面對制造品種、原材料種類繁多、客戶需求急迫和多樣化這些現實難題，企業不會輕易添置或更新昂貴的生產設備。如果產品剛好在成長期，將會出現生產能力短缺、交貨期延長等問題，會影響客戶滿意度，降低產品市場競爭力。因此，多品種小批量混流生產模式產生，這種生產方式很好地融合了大規模定制當中批量生產降低成本的優點，又盡可能地滿足了多品種的要求。

目前對于有關理論與技術的研究集中在面向約束管理的瓶頸分析管理、緩沖設置管理、加工批量設置和關鍵資源管理等方面[2-4]，涉及相關理論概念的描述、算法研究、緩沖大小的設置、負載率的分析以及一些基本的理論模型的建立等[5-6]。其關鍵技術體現在生產預測、混流路徑規劃與任務成組、瓶頸識別與瓶頸排產、緩沖設置等幾個方面。

本文從生產系統方面用約束管理的思想對混流生產展開研究，通過較好的生產預測為訂單的處理提供有力保障，降低了緊急訂單的突發狀況，使生產計劃的制定更加平穩；通過有效的約束管理，找到生產系統中存在的關鍵約束條件，以目標函數的形式求解得到較優的生產計劃，實現以系統的物流平衡取代生產能力平衡，最終取得系統運作綜合優勢。

1 混流生產系統技術體系

綜合相關研究，按進程實施混流生產方式分為生產預測階段、混流設計階段、混流控制階段。這3個階段構成混流生產體系的橫坐標；從層次上混流生產有目標層、方法層、技術層，這3個層次構成混流生產體系的縱坐標。混流生產系統體系如圖1所示。

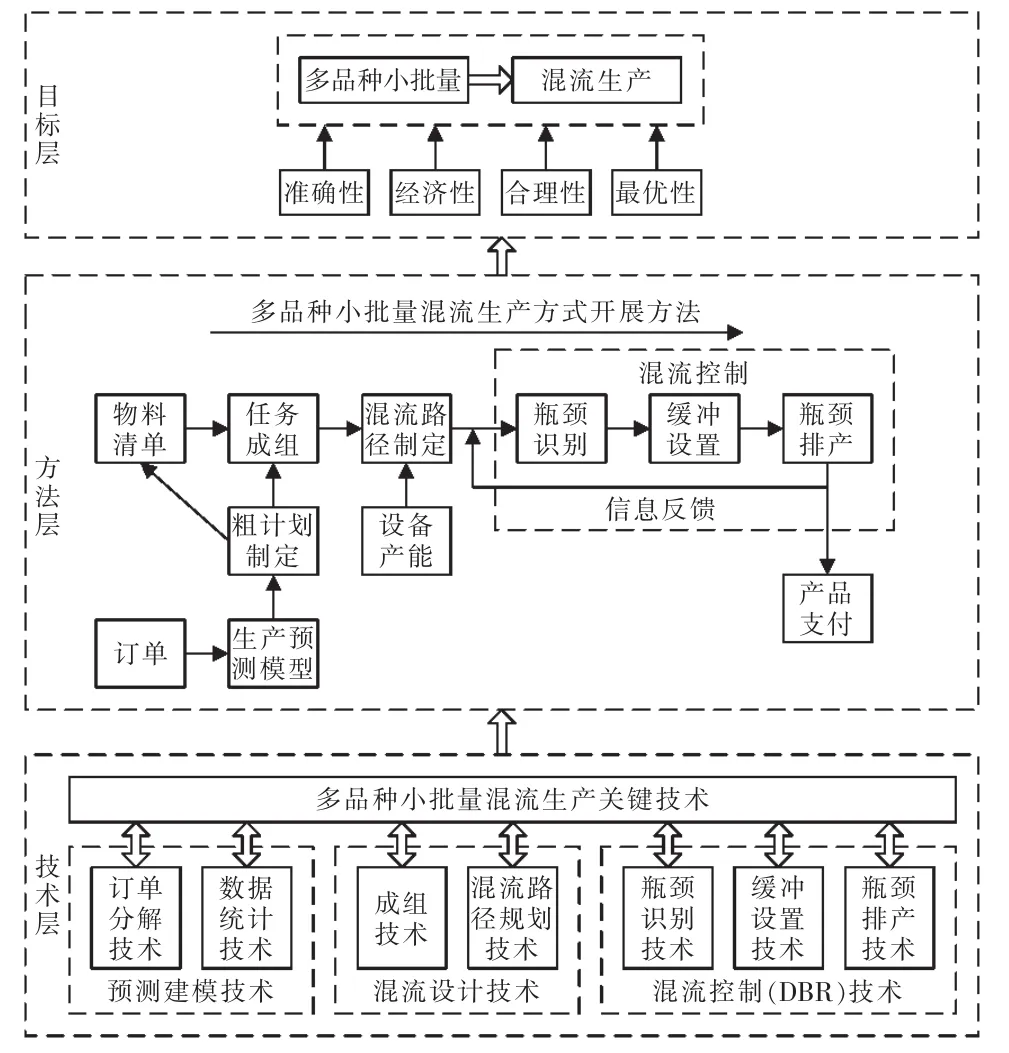
圖1 混流生產系統體系Fig.1 Mixed flow production system

2 生產預測

2.1 訂單處理

生產預測是后續生產活動的關鍵，但由于訂單品種多、數量差別大，需要對訂單進行合并處理。根據以往的訂單情況，通過數據統計，將訂單總集合拆分成按生產類別區分的子集合，取生產數量占統計數量前80%的產品為關重件，其余產品為普通零件，把關重件作為預測的對象構造出可靠合理的生產預測模型。

2.2 預測方法選擇

預測方法有合適、低費用、精準性等要求，目前時間序列預測的常見方法有指數平滑法、狀態空間模型、博克斯-詹金斯法等[7]。博克斯-詹金斯法需要大量的數據才能保證預測的準確性，對于品種多樣以及變化較快的訂單來說是不現實的。灰色預測法中的GM（1，1）模型[8]對于多品種的預測較為合適，建立GM（1，1）模型只需要一個數列，將訂單的某種零件數據設為原始數列X（0），對原始數列進行一階累加，生成后的新數列用矩陣表示為

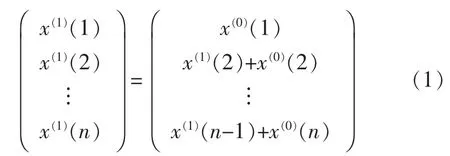
由于新數列是一階累加生成，與一階微分方程的解呈指數增長形式相似，因此，將新數列構造成一階線性微分方程模型：

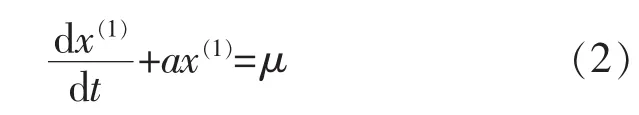
式中：x（1）是生成數列；a， μ 是待求參數。

最小二乘法求解此微分方程時，為計算方便，用離散形式表示微分項并由導數定義得到增量比：

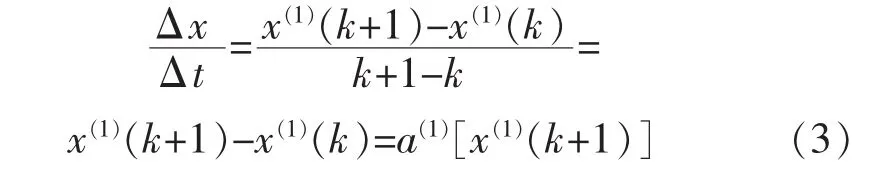
式中：x（1）值因為是離散量，只能取第 k個和 k+1個之間的平均值。微分方程式可寫成矩陣形式：

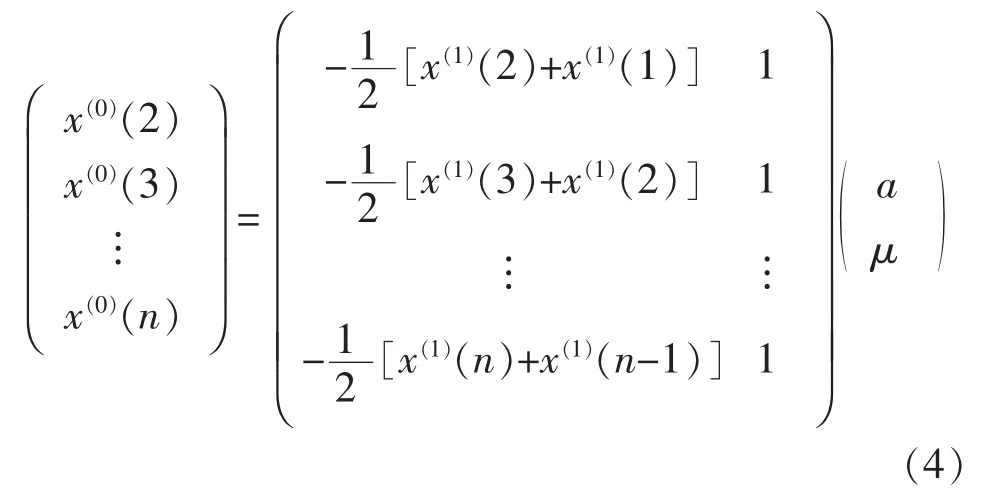
簡記為Yn=BA，用最小二乘法得到近似解即A陣估計值

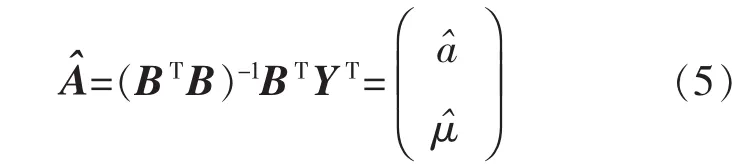
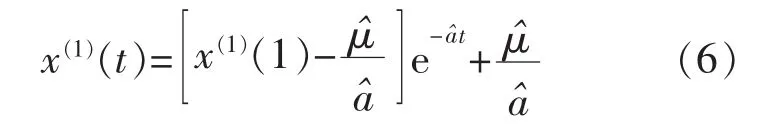
根據遞推累減關系，預測模型為

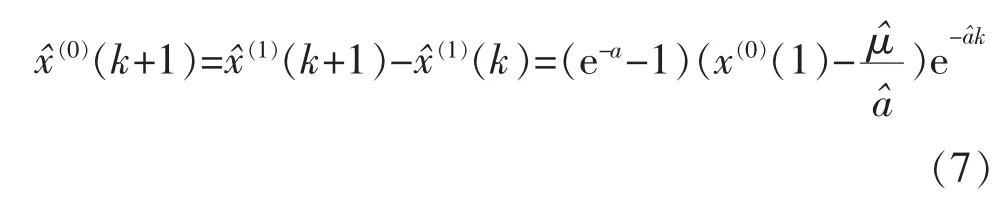
式中：k為整數。

3 混流設計

3.1 參數設計

訂單評估根據生產預測以及當前剩余生產能力對訂單完成的可能性進行評估，以確定是否接受某個具體訂單[9]。而任務投放是對所接受的訂單進行合理安排，根據訂單交期需求和車間現場負荷與產能現狀，準確及時地對訂單任務進行有節奏的投放。因此，在混流設計開始前需要將各參數用數學表達式表示出來作為輸入或者待求量，數學符號及意義如表1所示。

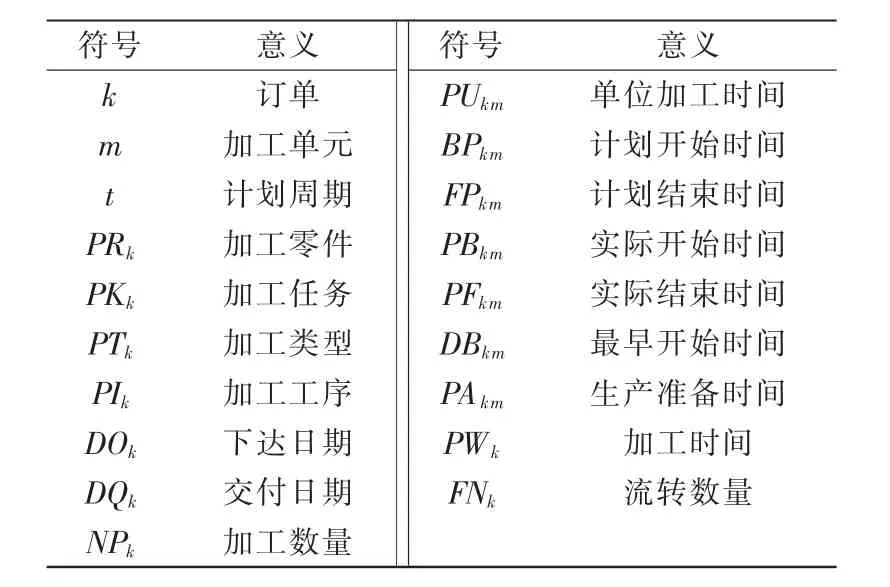
表1 數學符號與意義Tab.1 Mathematical symbols and significance

3.2 混流生產求解模型

3.2.1 決策變量與目標函數

決策變量設為

設定目標：所有訂單在計劃周期內完成，即

設備利用率表示為

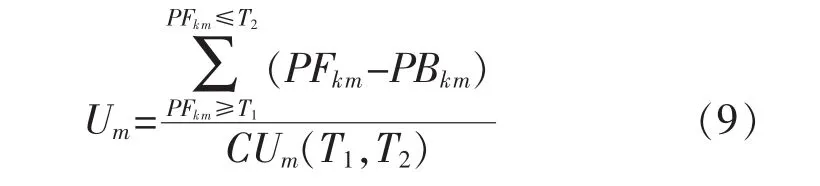
式中：CUm（T1，T2）表示某一設備在時間 T1，T2之間的工時。進一步使設備利用率最高，取設備利用率極值差最小為設備利用率最高，即

綜合目標即為

式中：λ1、λ2為常數，λ1+λ2為正整數 1。

3.2.2 約束條件

1）最早開工時間約束

最早開工時間應晚于任務下達時間，

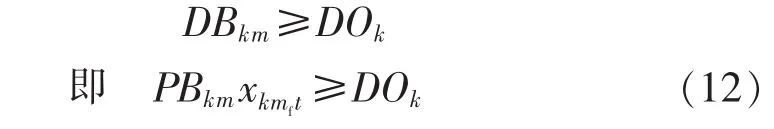
式中：xkmft為第一道工序決策變量。

2）工藝約束

離散生產方式下的零件，工序間有嚴格先后關系，所有的可調度工序都相同，流水生產方式下的零件，前序生產達到一定量生產后，后序即可展開，已經開始生產的零件可調度工序具有較高優先級。因此，混流生產的工藝約束表示為

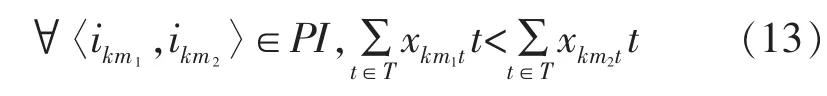
即緊后工序的開始前必須是緊前工序已經加工完成。

3）交期約束

交期約束表示為

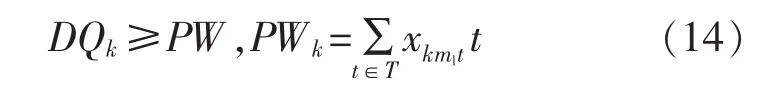
式中：xkmlt為最后一道工序的決策變量。

4）生產準備約束

緊后工序實際開始時間應在緊前工序完成后加上準備時間即

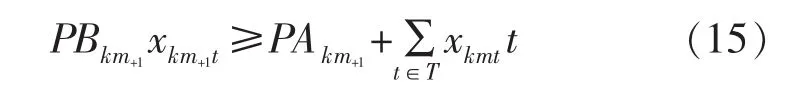
5）生產單元產能約束

生產單元產能約束表示為

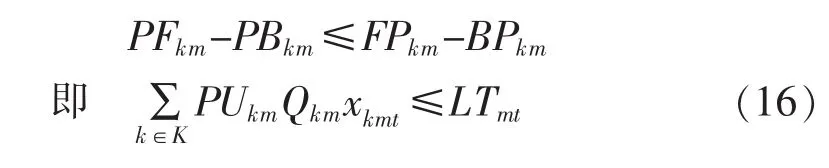
式中：Qkm為數量；LTmt為可用時長。

4 混流控制

離散生產方式下的零件，每一工序只能在特定的設備上生產并且所有的可選設備間可自由選擇，流水生產下的零件，加工時間較長的采用設備組，一般追求相似的加工時長，有邏輯單元優先選擇的特性。邏輯制造單元主要依據工廠的布局、設備的產能、以及任務狀況等基礎條件分析進行的混流路徑方案設計。所以在基于約束理論的混流生產中，不同產品的工藝特點和生產設備的使用會出現靜態和動態的混流生產線，并由此產生設備過多利用即瓶頸的情況。

混流控制階段主要應用Drum-Buffer-Rope（DBR）技術，在瓶頸處設置合理的緩存并使生產系統的節拍穩定。解決瓶頸問題的有效策略是在混流設計中均衡各設備利用率，避免出現單個設備利用率過高現象。緩沖設置中采用關重件（80%關重件）設備加工與普通（20%普通件）加工相結合的方式，即用普通零件加工提高利用率相對較低的設備，生產單元調控邏輯[11]如圖2所示。

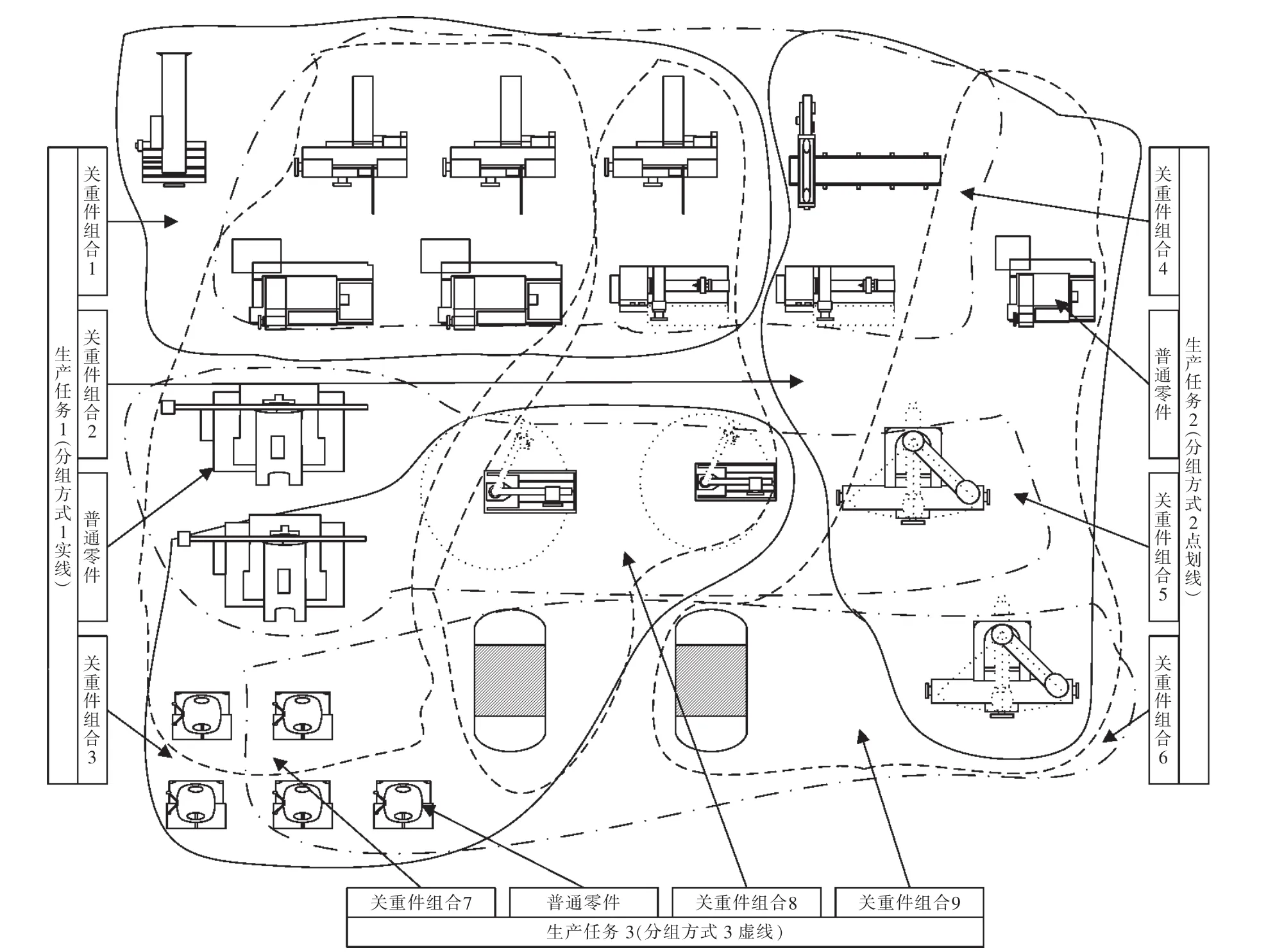
圖2 生產單元邏輯示意Fig.2 Schematic diagram of the logic unit production

5 訂單排產與分析

以某主要從事汽車配件如活塞、前輸出軸、頂柱體等冷擠壓產品生產的企業為研究對象，取上一季度銷售訂單數據，統計出活塞為主要產品，其中5785.9B型號活塞產量占到活塞總量的33.2%，為關重件。因此，以此型號產品為例，將訂單數據作為初始序列，得到預測值如表2所示。

從表2可以看出，最大預測相對誤差在13%以內，平均相對誤差（8.72%）在9%以內，預測精度達到90%以上，這對多品種、變批量企業來講是非常容易接受的。在生產排產時，以活塞為例，活塞的生產工藝依次為①鋸料、②拋丸、③磷皂化、④預成型、⑤磷皂化Ⅱ、⑥成型、⑦拋丸Ⅱ、⑧分選包裝。為簡化運算，將生產訂單分解成為在每個加工單元每日可以完成的工作量，算例數據如表3所示。

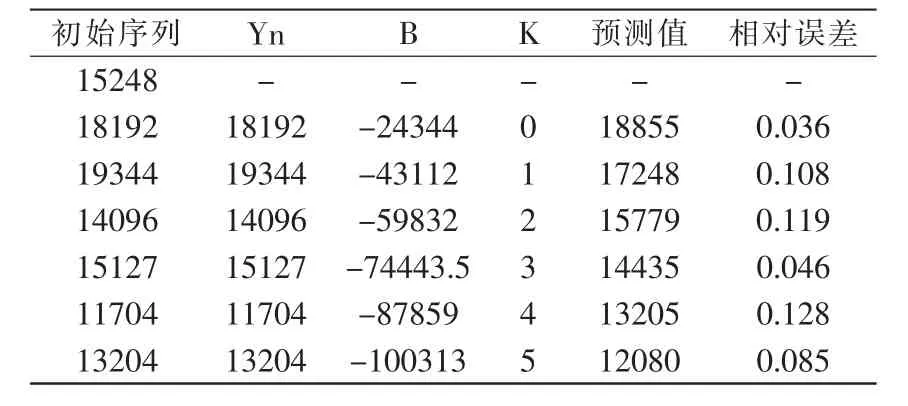
表2 預測值Tab.2 Predictive value

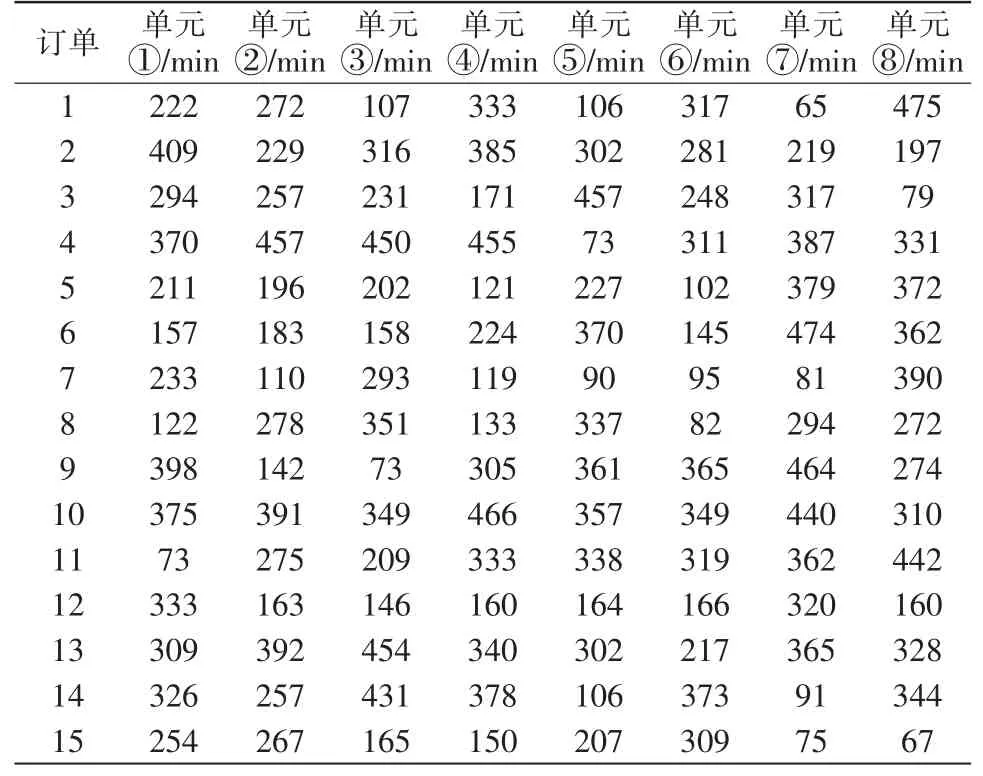
表3 算例數據Tab.3 Example data

每個生產單元的可用時長設定為每日8 h，計劃周期為20個工作日，生產提前期為1個工作日，生產準備時間設定為0。

事實上，生產預測階段在時間上相對獨立，混流設計和混流控制階段相互交叉，混流控制的結果作用于混流設計。因此，將混流控制階段的DBR技術應用到混流設計中，即對原活塞的生產工藝約束進行優化，如圖3所示。

圖3 活塞生產工藝Fig.3 Piston production process

從圖3可以看出，預成型工序前后都包含了拋丸、磷皂化工序，若各工序工時假設都為1個工作日，以預成型后的產品作為緩存，緩存量設置為1 d產量，則局部工藝離散后的產品生產周期為4 d，相較于之前需要8 d提高了一倍。

將所有參數輸入到生產模型中，用Lingo軟件可得到較優的方案，生產計劃如表4所示。

如表4中所示，第一天第一生產單元要完成訂單5、6、11的生產任務，用時441min。所有訂單在15 d內完成，比計劃時間提前5 d，各生產單元的日平均利用率最高為第四單元的84.8%（407 min），最低為第六單元的77.5%（372 min），生產單元間生產負荷相對均衡，總平均設備利用率在80%以上，達到了期望效果。

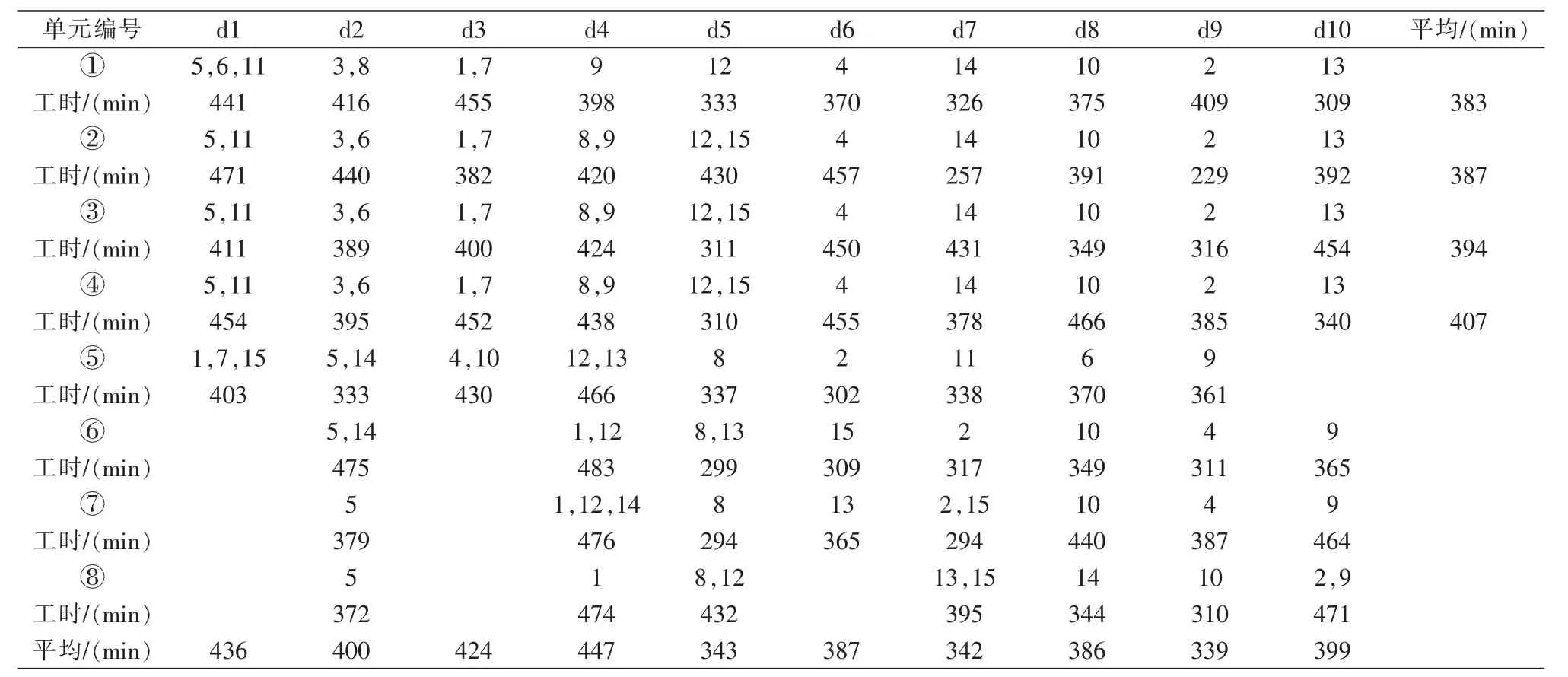
表4 生產計劃表Tab.4 Production schedule

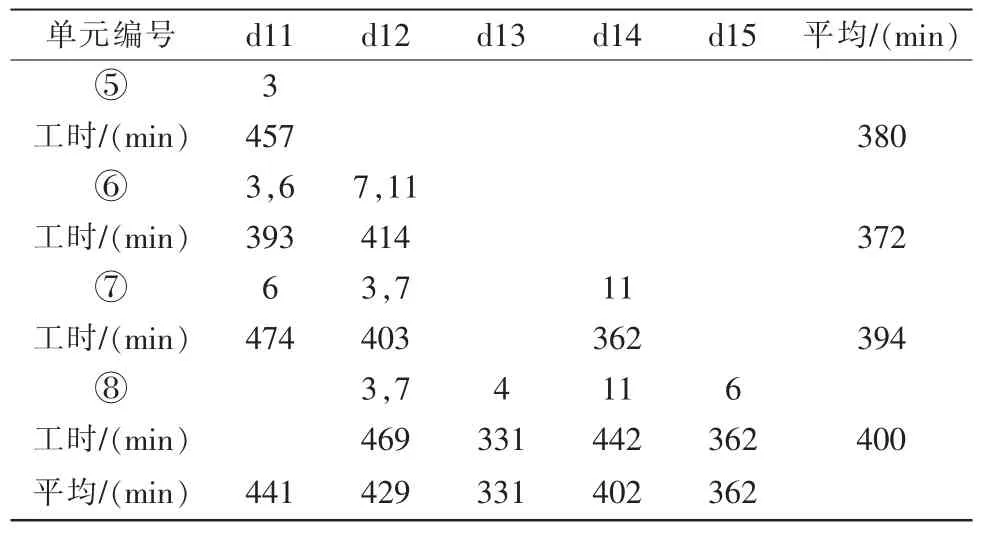
表4續

6 結語

本文提出的多品種變批量混流生產系統方法，首先按生產特性分成了3個階段，并對每個階段的輸出綜合性進行了建模，經企業生產數據的驗證后，能使訂單全部按時完成交付的同時，設備資源也有較高的利用率。在實際生產中，有待通過優化異常值訂單使預測更加準確，通過普通件插空生產與DBR技術的深度應用進一步提高設備利用率。

[1]韓文民，葉濤鋒.混流條件下基于TOC制定生產作業計劃的關鍵問題：研究現狀及發展探討[J].江蘇科技大學學報，2005，19（6）：92-95.

[2]Hamid Y，Mustafa Y.Multi-manned assembly linebalancing problem with balanced load density[J].Assembly Automation，2015，35（1）：137-142.

[3]劉勇，谷寒雨，席裕庚.基于約束理論的混合復雜流水線規劃調度算法[J].計算機集成制造系統，2005，11（1）：97-103.

[4]謝楠，李愛平，尤建新.支持混流生產的可重組邏輯控制器設計方法[J].計算機集成制造系統，2008，14（5）：842-848.

[5]D Wu，M Ierapetritou.Hierarchicalapproach forproduction planning and scheduling under uncertainly[J].Chemical Engineering and Processing.2007，46（11）：1129-1140.

[6]王時龍，易力力，任亨斌，等.多品種小批量成批成套生產滾動計劃的生成方法[J].2009，32（9）：1024-1027.

[7]王麗亞，陳友玲，馬漢武，等.生產計劃與控制[M].北京：清華大學出版社，2013：43-67.

[8]劉思峰，鄧聚龍.GM（1，1）模型的適用范圍[J].系統工程理論與實踐，2000，20（5）：121-124.

[9]楊志偉.多品種小批量面向訂單生產的動態排產研究[D].北京：清華大學，2009.

[10]王愛民.制造執行系統（MES）實現原理與技術[M].北京：北京理工大學出版社，2014：128-167.