非線性不等式約束優化問題的指數型精確罰函數算法

楊 蓮, 姚奕榮

非線性優化問題廣泛存在于工程設計、經濟管理、軍事科研等應用領域.許多學者開始把一些成熟的、有效的算法拓展到求解非線性優化問題中,其中罰函數算法較為引人注目.罰函數算法是求解約束優化問題的一類重要方法,也是一類比較有效的方法.

罰函數算法的基本思想是借助罰函數把約束問題轉化為無約束問題,進而利用無約束最優化方法來求解約束問題.Courant[1]首先提出外點罰函數算法,有效地將帶有約束的非線性優化問題轉化為無約束優化問題.針對非線性不等式約束優化問題,Carroll等[2]提出了內點罰函數算法.精確罰函數的概念由Eremin[3]和Zangwill[4]在20世紀60年代末分別提出.精確罰函數包括非光滑精確罰函數[5-6]和光滑精確罰函數[7].1967年,Zangwill[4]對凸優化問題提出了l1精確罰函數.自此,精確罰函數算法成為解決非線性優化問題的重要方法,人們對該算法開展了許多研究.Rosenberg[8]和Lasserre[9]分別研究了一個精確罰函數算法的全局收斂性.Pinar等[10]提出了一個一次連續可微的罰函數.K¨omer[11]研究了二次規劃問題的精確罰函數的數值算法.文獻[12]給出了精確罰函數的一個充要條件.在文獻[13]中,對于單值標量約束優化問題,Lucidi提出并證明了低階精確罰函數與原約束優化問題的等價性.對于變分不等式的約束優化問題,文獻[14]通過正則間隙函數提出了一個新的精確罰函數.對含有目標約束的優化問題,文獻[15]研究了罰函數的精確性并提出了相應的算法.由于表達式中含有目標函數或約束函數的梯度,在實際計算工作中會顯得過于復雜,大大制約了這類可微精確罰函數算法的實際應用.因此,非線性精確罰函數算法和低階罰函數算法得到了廣泛的關注,在許多新領域不斷有研究成果出現.針對箱子約束的等式優化問題,文獻[16]通過增加一個變量,給出了一個新的精確罰函數.

受文獻[16]的啟發,本工作主要通過增加一個變量,針對非線性不等式約束優化問題構造了一個新的指數型光滑精確罰函數,并證明了該罰函數在集合{(x,ε)|ε=0,x∈S或0＜ε＜ε}上具有二次連續可微性和精確性質.最后,基于牛頓法設計了一種新的指數型精確罰函數算法,并通過數值計算驗證了算法的可行性.

1 指數型光滑精確罰函數

1.1 罰函數的構造

考慮非線性不等式的約束優化問題:

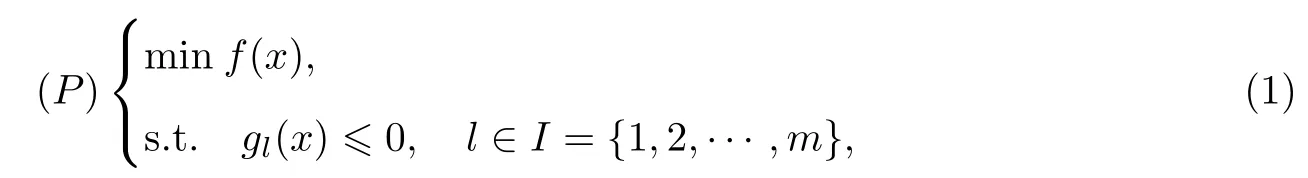
式中,函數f,gl:Rn→R是二次連續可微函數.另記S={x∈Rn:gl(x)≤0,l∈I}.

通過增加一個變量ε,問題(P)等價于

式中,ωl∈ R+為給定的實數.另記 Sε={(x,ε):gl(x)≤ εγωl,l∈ I}.構造相應的罰函數

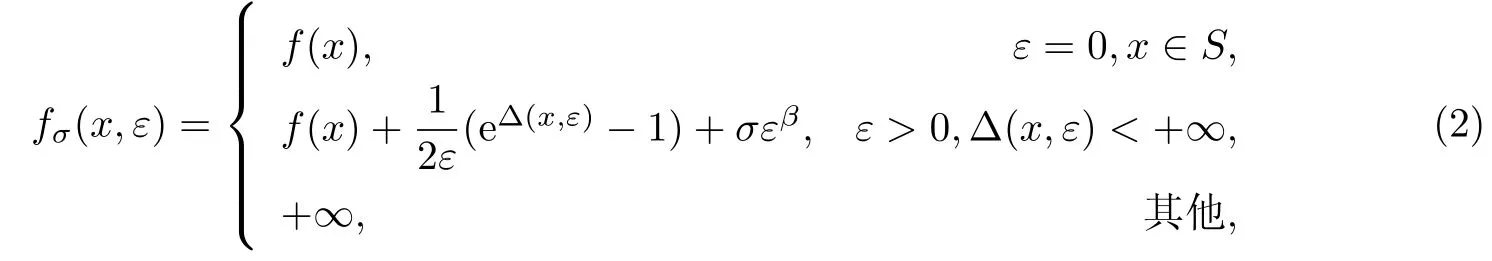
考慮問題(P)的罰問題

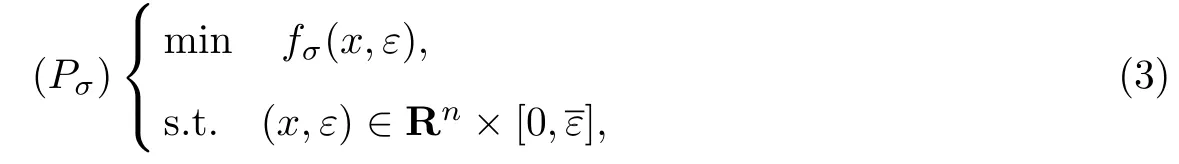
式中,ε＞0是一固定的實數.顯然,問題(Pσ)是一個無約束優化問題.事實上,當罰參數足夠大時,問題(Pσ)的任何局部極小點都是問題(P)的局部極小點.下面對問題(P)做出一些假設:(1)f(x)在可行域S上是下有界的,其中S是一個緊集或是一個無界閉集;(2)x?∈L(P)是孤立的點,L(P)的數量是有限的,其中L(P)表示問題(P)的局部極小點的集合.

若x∈/S且 ε＞0,Δ(x,ε)＜+∞,fσ(x,ε)=f(x)+(eΔ(x,ε)? 1)+ σεβ＞ f(x),則當 Sn是一個無界閉集合且f(x)在S上是下有界時,顯然fσ(x,ε)在集合{(x,ε)∈R×[0,ε]:ε =0,x∈S或者ε＞0,Δ(x,ε)＜+∞}中是下有界的.當S是一個緊集,則對于ε＞ 0,fσ(x,ε)在集合{(x,ε)∈Rn×[0,ε]:ε=0,x∈S或者ε＞0,Δ(x,ε)＜+∞}上是下有界的.因此,fσ(x,ε)在集合 Rn× [0,ε]上是有下界的,這表明 fσ(x,ε)在 Rn×[0,ε]上存在局部極小值.

1.2 罰函數的光滑性

設{σk}是一遞增的罰參數序列,σk→+∞.對固定罰參數σk,記對應的罰問題(Pσk)的最優解為(xk,εk).為了證明罰函數的光滑性和精確性,作如下假設.

(1)函數f,gl,l=1,2,···,m在Rn上是二次連續可微的.

(2)M-F約束品性在x?處成立,即如果存在h∈Rn使得對所有的j∈J(x?),有?gi(x?)Th＜0,其中J(x?)={j∈ I|gj(x?)=0},x?是問題(P)的局部極小點.

(3)max{0,gl(x(k))}=o((ε(k))σ),σ ＞ 1,l=1,2,···,m.

定理1 若(xk,εk)滿足假設(1)～(3),γ,β,N 滿足2N+γ?3＞0,N?2＞0,Nγ?3＞0,β ? 2＞ 0,則當 (x,ε)∈ {(x,ε)∈ Rn×[0,ε]:ε＞ 0,Δ(x,ε)＜ +∞},且 ε→ 0,x→ x?∈ S時,有

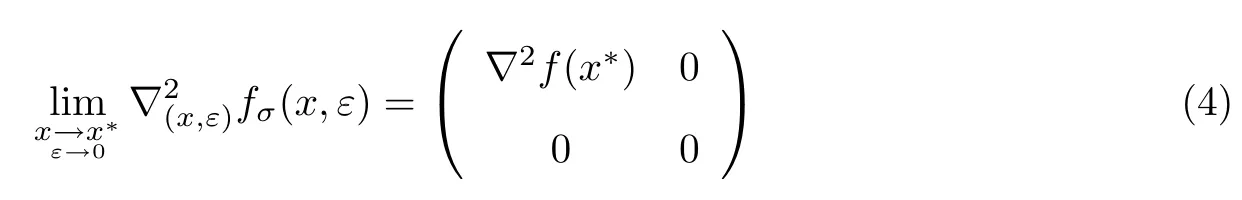
成立,其中

證明 (1)當 ε=0 時,由 fσ(x,ε)的定義可知 fσ(x,ε)=f(x).因此,

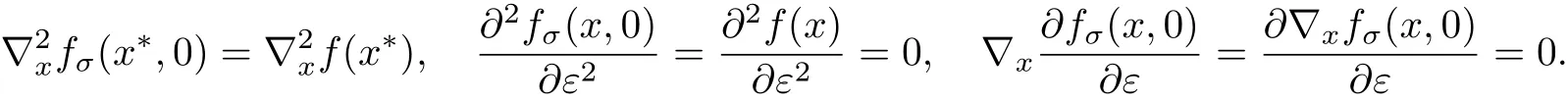
(2)當 ε/=0,(x,ε)∈ {(x,ε)∈ Rn×[0,ε]:ε＞ 0,Δ(x,ε)＜ +∞},由 fσ(x,ε)的定義可知

因此,有

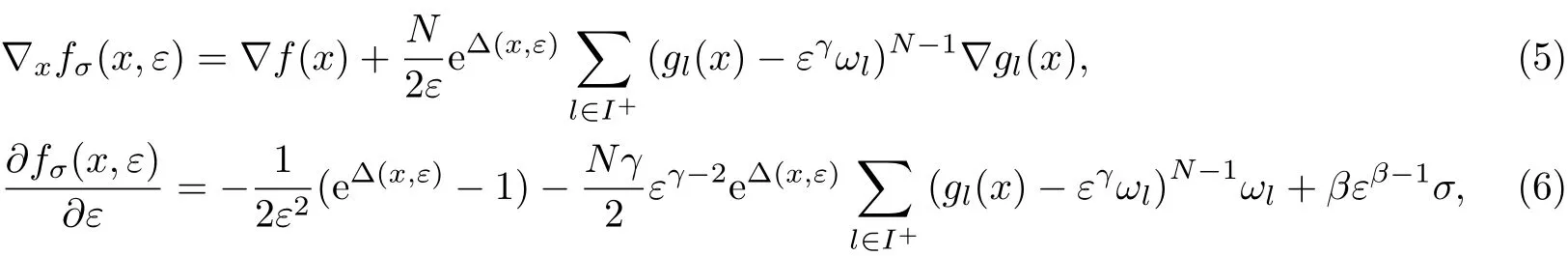
由式(9)和(10)可得,

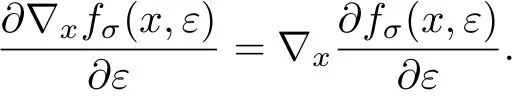
下面證明當ε→0,x→x?∈S時,

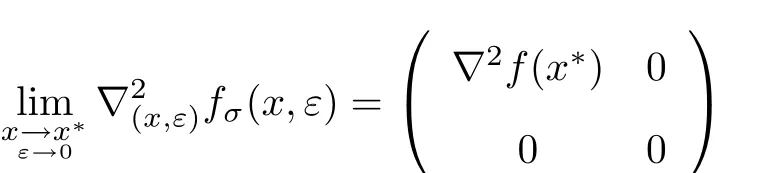
成立.

當ε/=0,ε→0,x→x?∈S時,由假設(3)可得

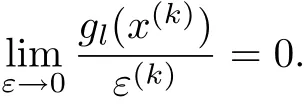
由式(7),(8),(9)和(10)可知,若令γ,β,N 分別滿足

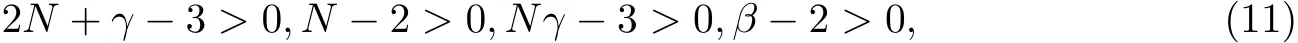
則有

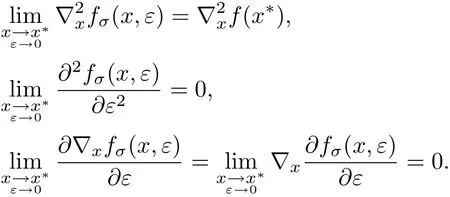
因此,有

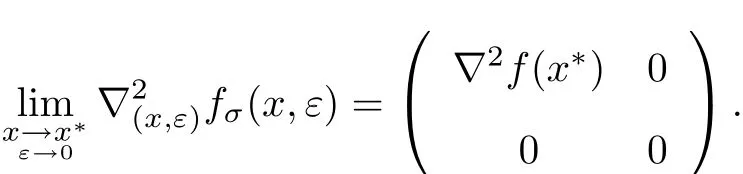
定理得證.定理1表明本工作構造的罰函數是二次連續可微函數.

1.3 罰函數的精確性

下面證明罰問題(Pσ)的局部極小點序列(xk,εk)將會收斂到問題(P)的局部極小點.

引理1 令(xk,εk)是問題(Pσk)的一個局部極小點,且函數值fσk(xk,εk)有限,εk＞0.則(xk,εk)/∈Sε={(x,ε):gl(x)≤εγωl,l∈I}.

證明 若 (xk,εk)∈ Sε,由于 (xk,εk)是罰問題 (Pσk)的一個局部極小點且函數值fσk(xk,εk)為有限值,εk＞ 0,從而有

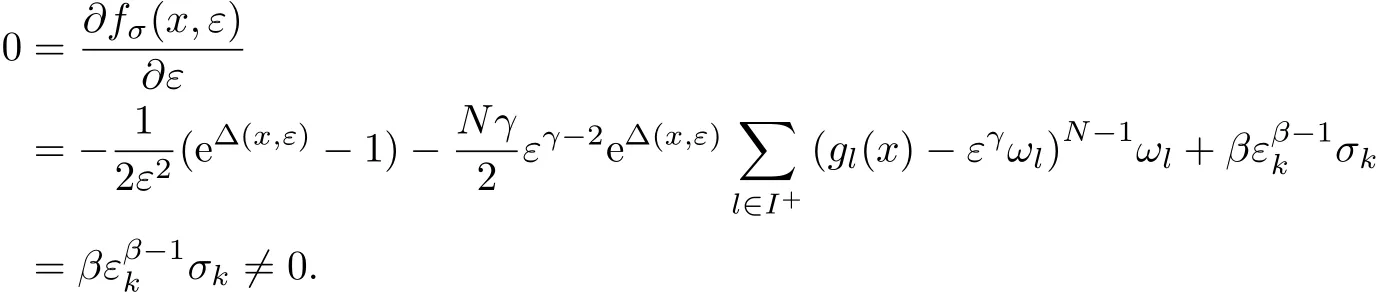
顯然,上式矛盾.因此有(xk,εk)/∈Sε.

定理2 設(xk,εk)是罰問題(Pσk)的局部極小點,函數值fσk(xk,εk)有限,εk＞0.如果k → +∞,(xk,εk)→ (x?,ε?)滿足假設條件(1)～ (3),那么有 ε?=0,x?∈ S.

證明由引理1可知,(xk,εk)/∈Sε,于是有?(x,ε)fσk(xk,εk)=0.因此,有

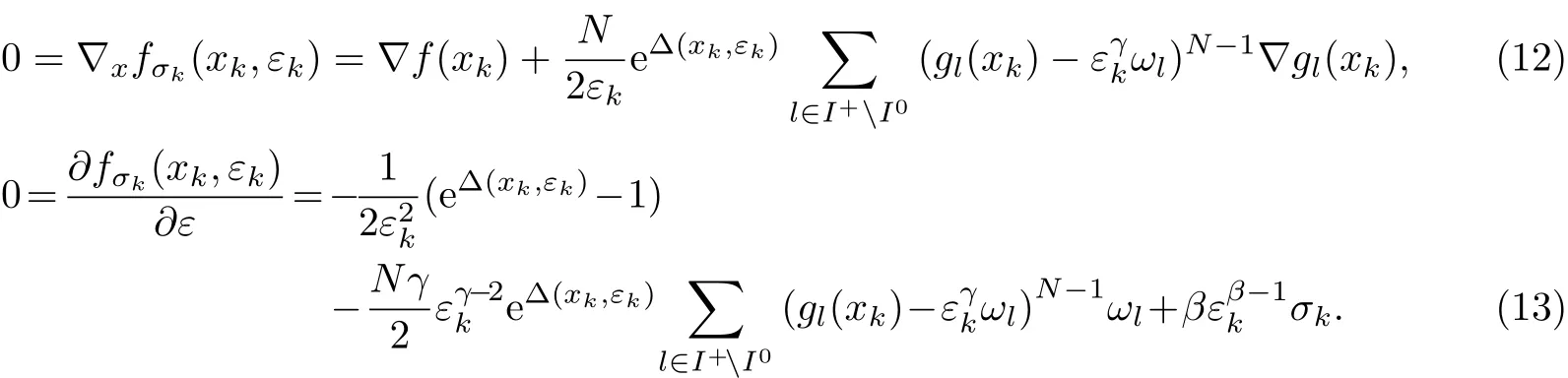
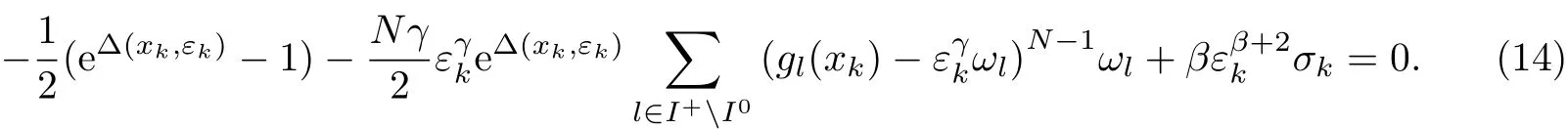
如果ε?/=0,則當σk→+∞,εk→ε?,xk→x?時,式(14)的第一項和第二項均為有限值,第三項則趨于無窮大,等式不可能成立,因此,εk→ε?=0.此外,由式(12)可知,當εk＞0時,

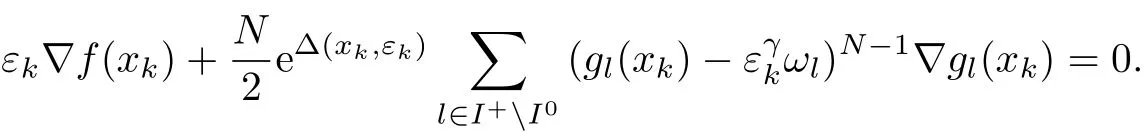
當σk→+∞,εk→ε?=0時,可以得到

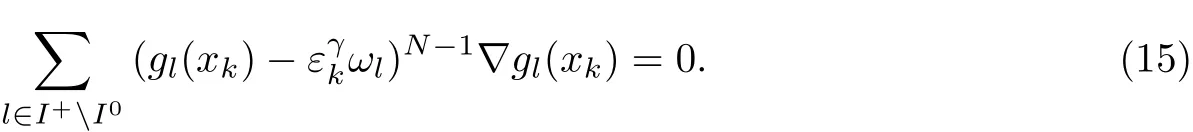
下面證明I+=I0.假設I+/=I0,則存在l0∈I+I0,使得gl0(x?)＞0.由于在x?處滿足假設條件(2),因此存在p∈Rn,p/=0,使得?Tgl0(x?)p＜0,l0∈I+I0,由此可得

顯然上式與式(15)矛盾.因此,I+=I0,且x?∈S.

引理1和定理2表明局部極小點的序列{(xk,εk)}將收斂到問題(P)的可行解且具有有限的目標函數值,且這個可行解是問題(P)的局部極小點.

下面證明所構造的罰函數fσ(x,e)是精確的.

定理3 假設定理2和條件(式(11))成立,則存在k0＞0,使得對任意的k≥k0＞0,都有εk→0,xk∈L(P)成立.

證明 假設結論不成立,則存在序列{(xk,εk)}的子序列{(xnk,εnk)},使得對任何k0＞0,都存在k′＞k0,且滿足εk/=0.根據定理2,有

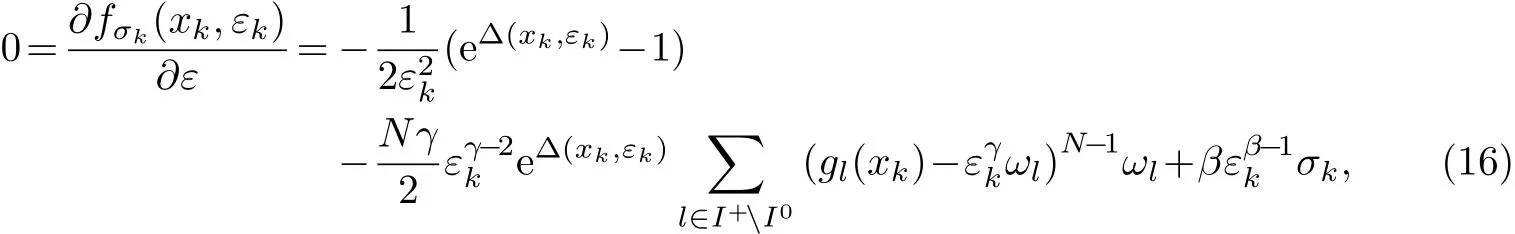
簡化上式,可得

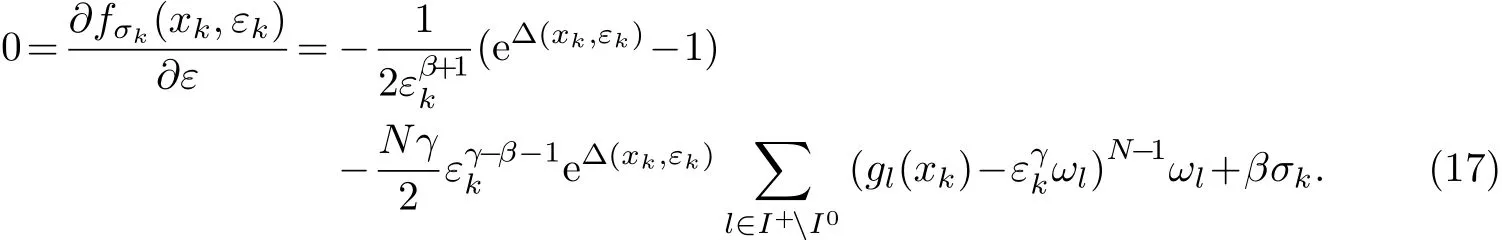
當k→+∞,由定理2可知,εk→ε?=0,xk→x?∈S.因為式(17)的第一項和第二項為有限值,而式(17)的第三項趨于∞,所以式(17)矛盾,因此子序列{(xnk,εnk)}不存在.故定理為真.

定理1和定理3表明所構造的罰函數是光滑的和精確的.

2 罰函數算法及數值計算

2.1 罰函數算法

第1步 選擇適當的(x0,ε0)∈Rn×[0,ε],ε＞0使得Δ(x0,ε0)＞0,σ0＞1足夠大,δ＞0足夠小,H0是一正定矩陣.令k:=0.

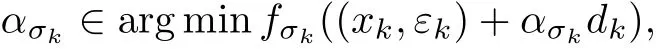
Hk是一正定矩陣.再令ασk滿足

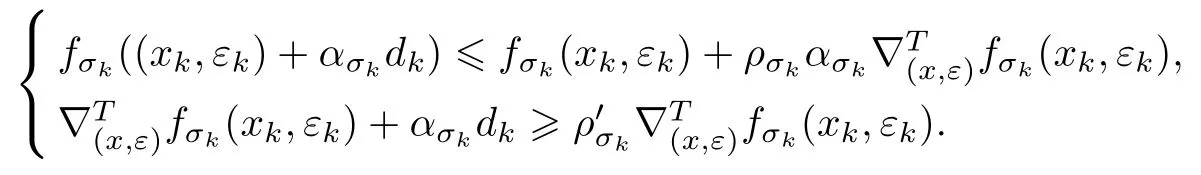
第 4 步 令 (xk+1,εk+1)=(xk,εk)+ασkdk,σk+1=cσk,其中c＞1 為常數.

第5步 令k:=k+1,返回第2步.

2.2 數值計算

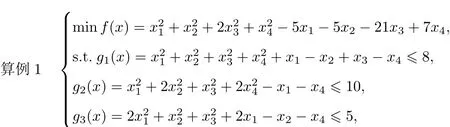
此問題的最優解和最優值分別為=(0,1,2,?1)和f(x?)=?44.在本算例中,取x0=(0.5,1.5,1.5,?1.5),ε0=2.0,N=8,α=6,β=4,ω=0.05.運用Matlab 7.11軟件計算,結果如表1所示.

表1 算例1的數值計算結果Table 1 Numberical calculation results of Example 1

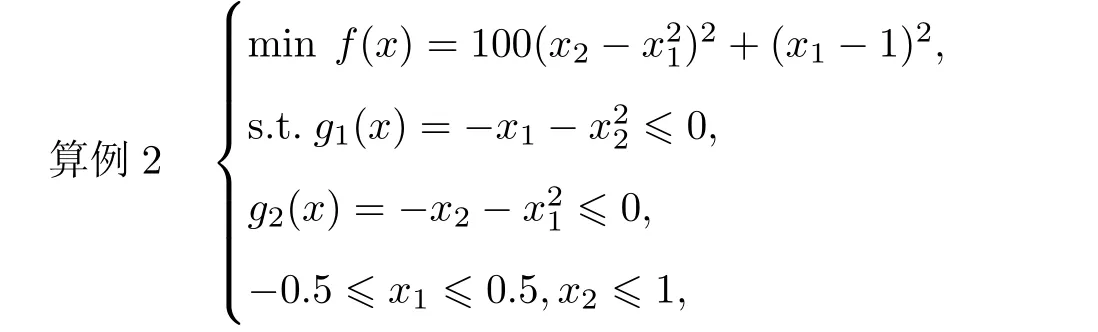
此問題的最優解和最優值分別為x?=(0.50,0.25)和f(x?)=0.25.在本算例中,取x0=(?1,0),ε0=1.0,N=4,α=4,β=4,ω=0.05.運用Matlab 7.11軟件計算,結果如表2所示.

表2 算例2的數值計算結果Table 2 Numberical calculation results of Example 2

算例1和算例2表明,通過選擇合適的參數可以得到原問題的近似最優解,從而說明所設計的罰函數算法是可行的.

3 結束語

本工作針對非線性不等式約束優化問題,通過加入一個變量構造了一種新的指數型光滑精確罰函數,并對罰函數的光滑性和精確性進行了討論.另外,還設計了求解原問題的精確罰函數算法.對于大規模的優化問題,如何提出一種更好的算法,需要進一步的研究和討論.

[1]COURANT R.Variational methods for the solution of problems of equilibrium and vibrations[J].Bulletin of the American Mathematical Society,1943,49:1-23.

[2]CARROLL C W,FIACCO A V.The created response surface technique for optimizing nonlinear restrained systems[J].Operations Research,1961,9(2):169-184.

[3]EREMIN I I.The penalty method in convex programming[J].Cybernetics and Systems Analysis,1967,3(4):53-56.

[4]ZANGWILL W I.Nonlinear programming via penalty function[J].Management Science,1967,13(5):344-358.

[5]ANTCZAk T.Exact penalty function method for mathematical programming problem involving invex function[J].European Journal of Operational Research,2009,198(1):29-36.

[6]ZASLAVSkI A J.Existence of exact penalty for constrained optimization problems in Metric spaces[J].Set-Valued Analysis,2007,15(3):223-237.

[7]ZHENG F Y,ZHANG L S.New simple exact penalty function for constrained minimization[J].Applied Mathematics and Mechanics(English Edition),2012,33(7):951-962.

[8]ROSEBERG E.Globally convergent algorithms for convex programming with applications to geometric programming[J].Mathematics of Operations Research,1981,6(3):437-443.

[9]LASSERRE J B.A globally convergent algorithm for exact penalty functions[J].European Journal of Operational,1981,7(4):389-395.

[10]PINAR M C,ZENIOS S A.On smoothing exact penalty functions for convex constrained optimization[J].SIAM Journal on Optimization,1994,4(3):486-511.

[11]K¨OMER F.On the numerical realization of the exact penalty method for quadratic programming algorithm[J].European Journal of Operational Research,1990,46(3):404-409.

[12]張連生.全局精確罰函數的一個充要條件[J].數學年刊(A輯),1997,18(5):579-586.

[13]LUCIDI S.New results on a continuously diあerentiable exact penalty function[J].SIAM Journal on Optimization,1992,2(4):558-574.

[14]LI W,PENG J.Exact penalty functions for constrained minimization problems via regularized gap function for variational inequalities[J].Journal of Global Optimization,2007,37(1):85-94.

[15]MENG Z Q,DANG C Y,JIANG M,et al.Exactness and algorithm of an objective penalty function[J].Journal of Global Optimization,2013,56(2):691-711.

[16]HUYER W,NEUMAIER A.A new exact penalty function[J].SIAM Journal on Optimization,2003,13(4):1141-1158.