彈性基底粘接薄板起皺的非局部分析

彭香武,趙建中,郭興明

微納米薄膜/基底結構系統在納機電系統(nano electro-mechanical system,NEMS)中有著十分重要的地位.在復合微納電子組件(薄膜、基底、封裝)生產過程中,由于熱學與力學參量的失配,薄膜在各種成型工藝過程的加熱冷卻,會引起殘余熱應力或錯位應變,從而使得NEMS失效.事實上,Bowden等[1]和Chen等[2]通過實驗發現,彈性基底加熱后粘合一層薄膜,待系統冷卻后,未脫粘的薄膜會自發形成有序的結構(起皺或屈曲).對于薄膜/基底系統,薄膜發生起皺失穩但仍未脫粘.Allen[3]通過研究夾層板模型,得出臨界薄膜力由基底的模量所決定的結論.Cerda等[4]對薄膜起皺的幾何和物理原理進行了闡述.Chen等[5]和Song等[6]分別使用數值法和解析法對3種起皺模態所具有的勢能進行了分析,其中基底被模擬為半無限空間.Huang等[7]和Li等[8]根據實際基底為有限厚的情況,分別對條紋形和棋盤形的起皺模態進行了非線性分析.Zhou等[9]研究了石墨烯圓片覆蓋在球基體上的非局部起皺行為.通過與分子動力方法的模擬結果比較,Yakobson等[10]發現連續介質力學模型在微納尺度器件的力學問題具有相當的有效性.關于微納尺度的研究表明需要建立更為精確的理論.Eringen[11-12]通過取消“局部化假設”建立了非局部理論,認為一點處的應力應與整個變形物體的應變有關.Pradhan等[13-14]和Behfar等[15]利用非局部理論研究了納米板和石墨烯的振動問題.Peng等[16]和劉亮等[17]利用非局部理論對復合粘接材料系統屈曲進行了尺度分析.

本工作研究了粘接在彈性基底上的薄板的單軸受壓起皺問題,利用彈性屈曲理論和非局部理論分別對薄板和彈性基底進行了建模,其中界面條件遵循“位移連續”和“零剪切應力”,分析了彈性基底的下表面條件、泊松比以及彈性基底與薄板的厚度比、模量比對薄板系統起皺行為的影響.模型的計算結果對微納尺度復合材料系統的構建具有參考意義.

1 理論模型與屈曲分析

薄板/彈性基底系統的條紋形起皺如圖1所示.由圖可以看出,厚度為h的薄板完全粘接在厚度為H的彈性基底上.薄板和彈性基底的彈性模量分別為Ep,Es,泊松比分別為μp,μs.單軸受壓的薄板發生條紋形起皺,且起皺過程中薄板和彈性基底粘接完好.

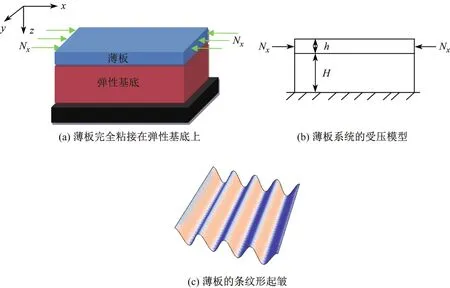
圖1 彈性基底上粘接薄板的條紋形起皺Fig.1 Stripes wrinkle of thin plate bonded on an elastic substrate

1.1 薄板的屈曲控制方程

由Kirchhoあ板假設可知,薄板上點(x,y,z)的位移場為

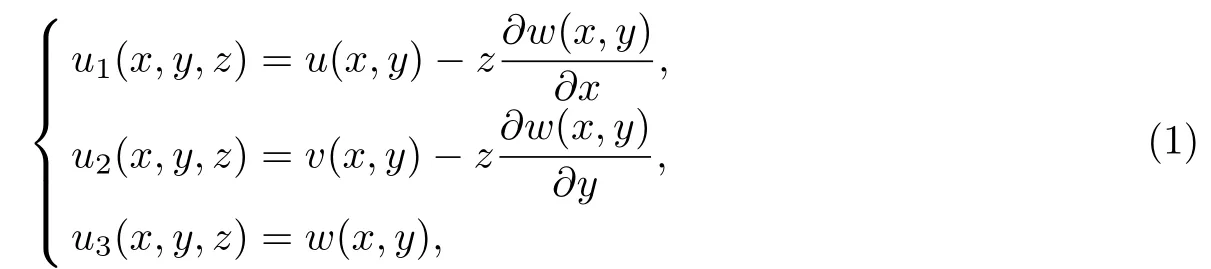
式中,u,v,w為中面上對應點的位移.

薄板的幾何方程為

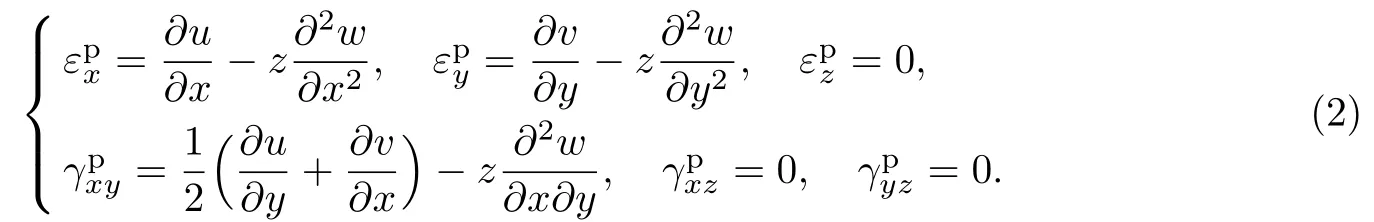
非局部本構方程可表示為[12,16]

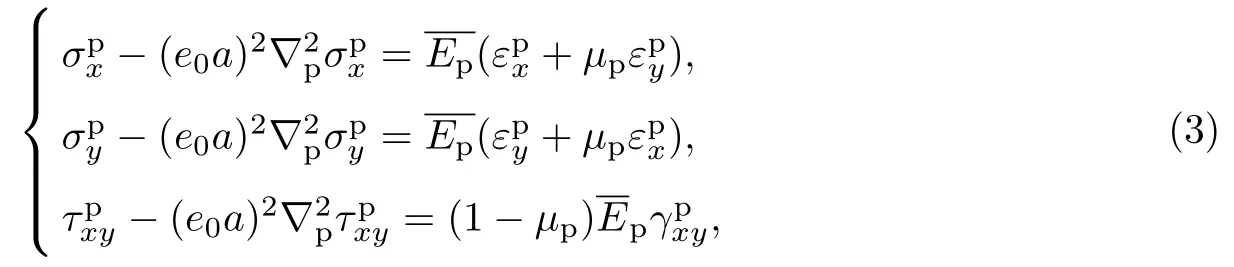
薄板的內力和內力矩可表示為

把式(3)代入式(4),則有

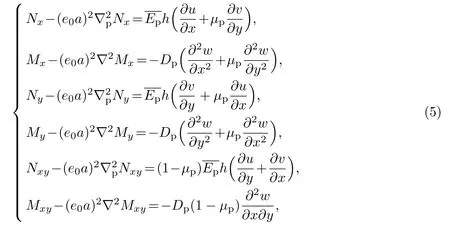
若不計體力,則薄板的力和力矩的平衡方程為

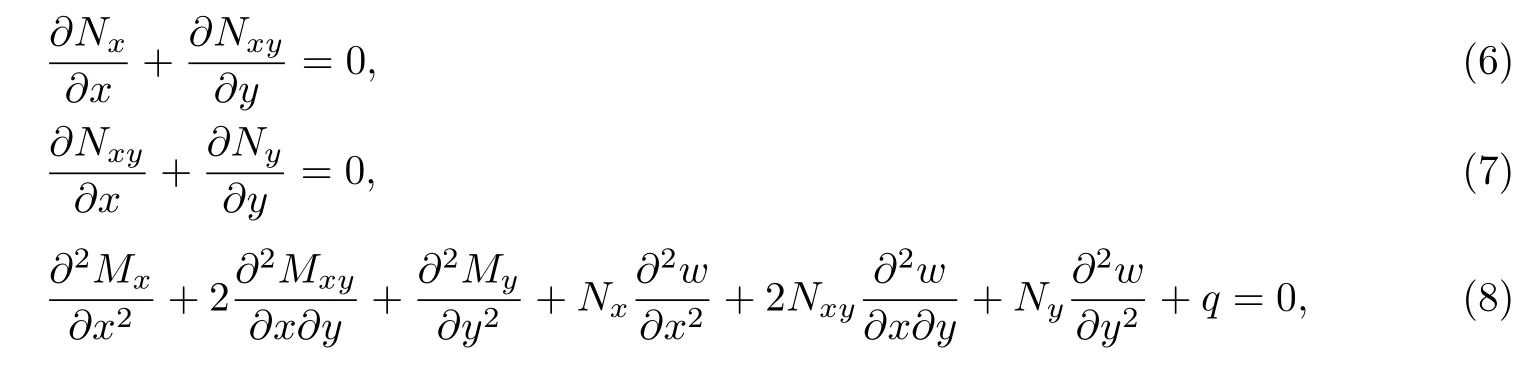
式中,q表示彈性基底對薄板的法向作用.

令Nx=N,Ny=0,Nxy=0,則其自然滿足式(6)和(7).同時,彈性基底等效為Winkler彈性后,應有q=Kww,其中Kw為對應變形的Winkler彈性系數.薄板的非局部屈曲控制方程可表示為

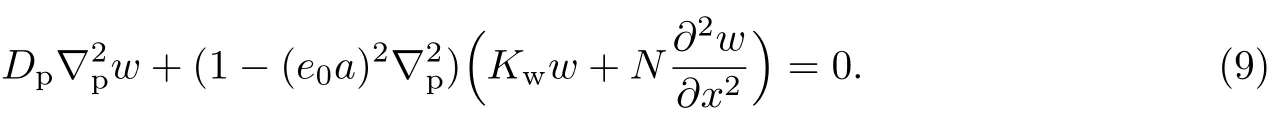
若考慮薄板的條紋形模態屈曲,則有w=Acos(kx).將其帶入式(9),可得

1.2 Winkler彈性系數的計算

當薄板發生條紋形模態起皺時,彈性基底也相應地發生變形,如圖2所示.

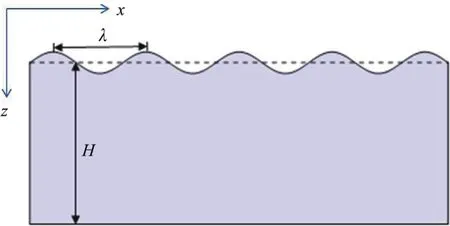
圖2 彈性基底的變形Fig.2 Deformation of elastic substrate

設彈性基底上點(x,z)的位移為(ux,uz),則其應變為

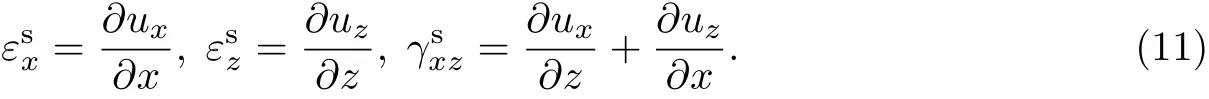
從而,應變協調方程可表示為

彈性基底的非局部本構方程為[12]

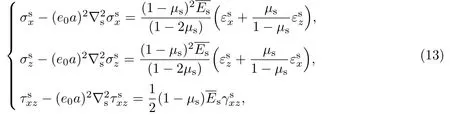
若忽略體力,彈性基底的受力平衡方程為

聯立式(12),(13)和(14),可推得應力函數表示的相容方程為

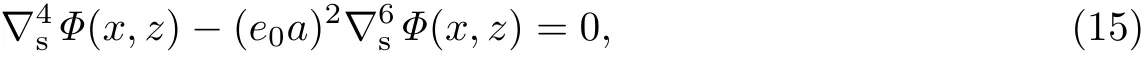
相應的應力分量分別為

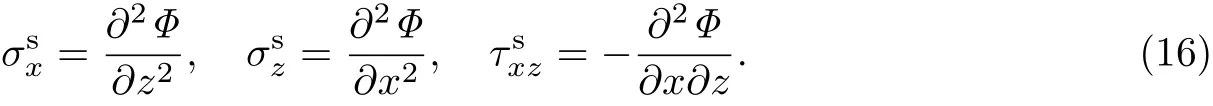
假設應力函數Φ(x,z)=F(z)cos(kx),將其代入相容方程(15),整理可得

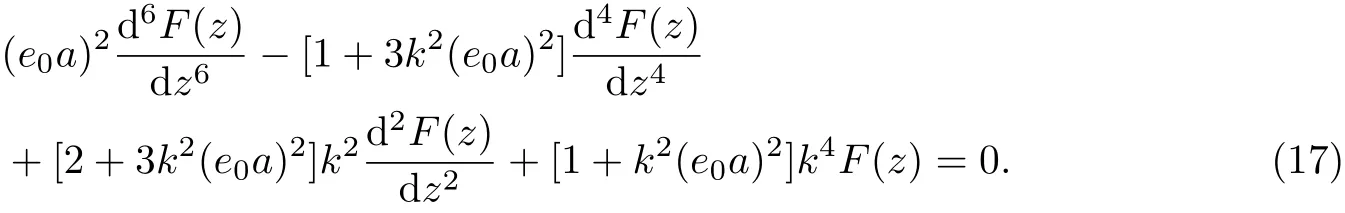
特征方程為

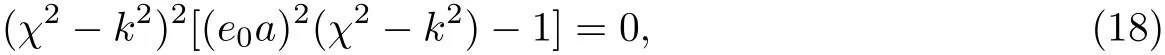
其特征根為

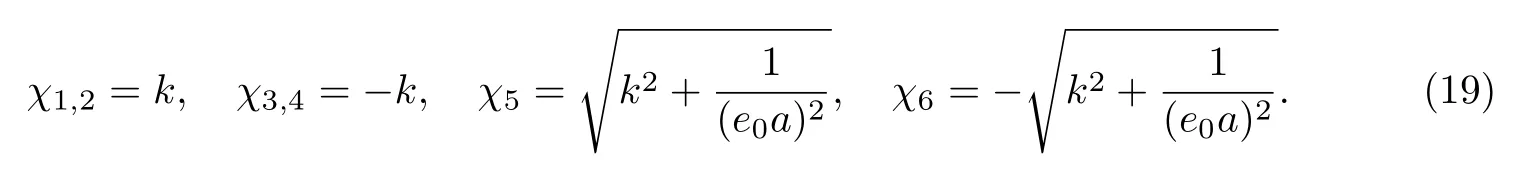
因此,方程(17)的解為

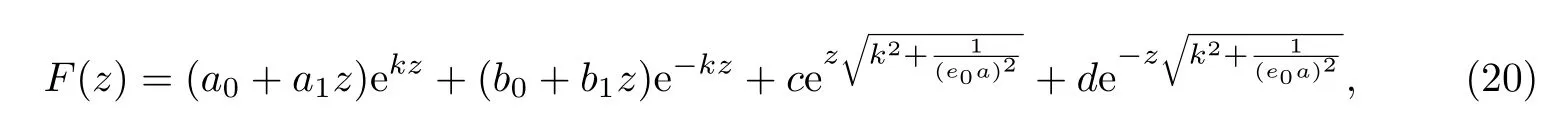
式中,a0,a1,b0,b1,c,d都是待定系數.

從而,所求的應力函數為

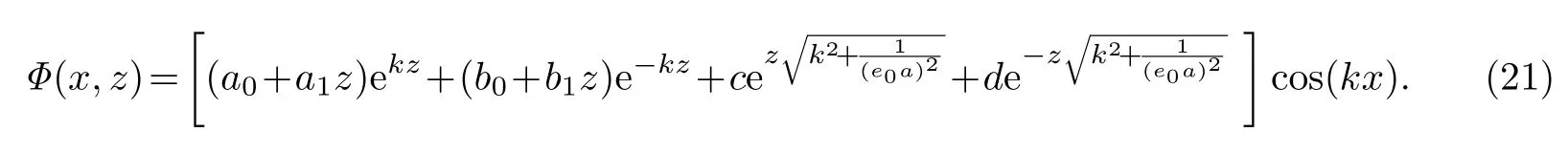
進而,相應的應力分量分別為

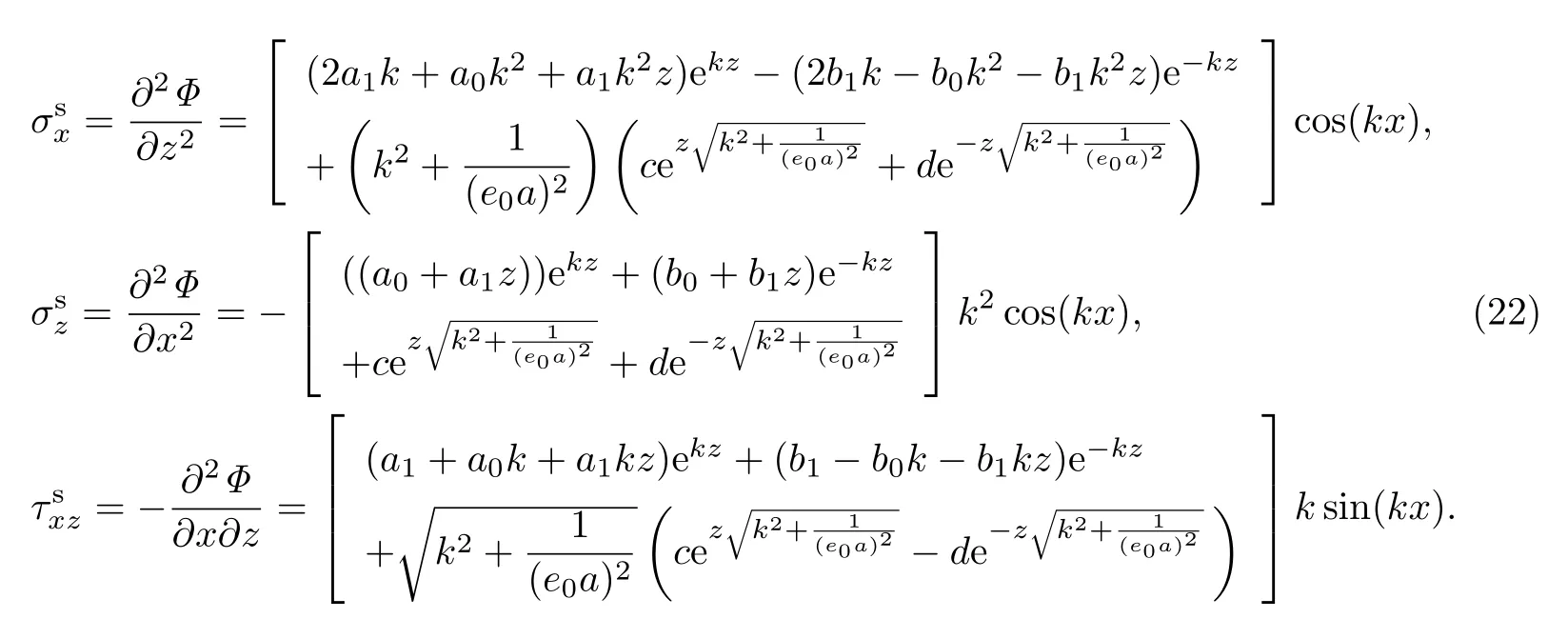
對應的位移分別為

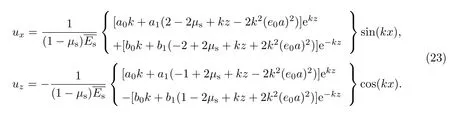
下面考慮彈性基底的邊界條件.若彈性基底下表面為完全粘接界面,此時彈性基底上表面與表層板粘結,其變形應與薄板的條紋形模態一致,且剪應力為0,下表面與剛性支撐完全粘接,其位移也為0,即有

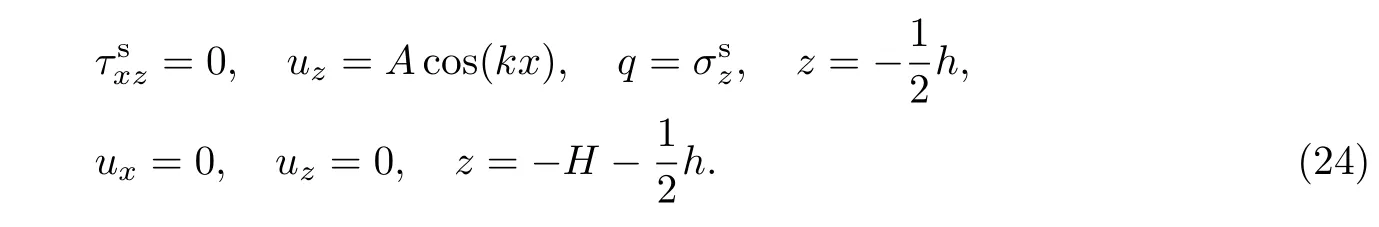
另外,當非局部參數退化為0時,應有

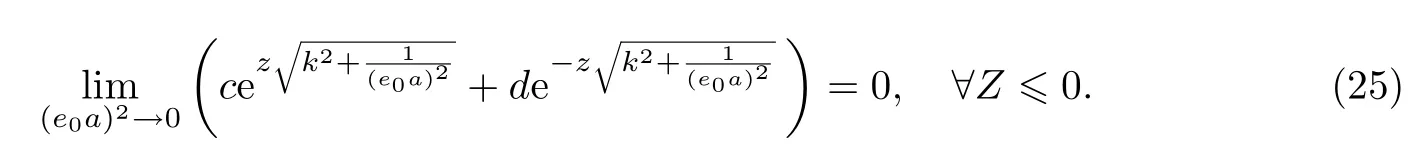
聯立式(24)和(25),最終得到Winkler彈性系數為

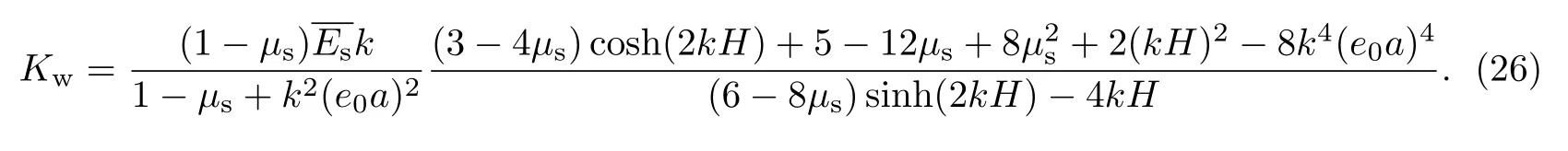
若彈性基底的下表面為滑動界面,則彈性基底的下表面所受剪應力為0.同時,彈性基底的上表面與薄板粘結,其變形應為條紋形,且剪應力為0.因此有

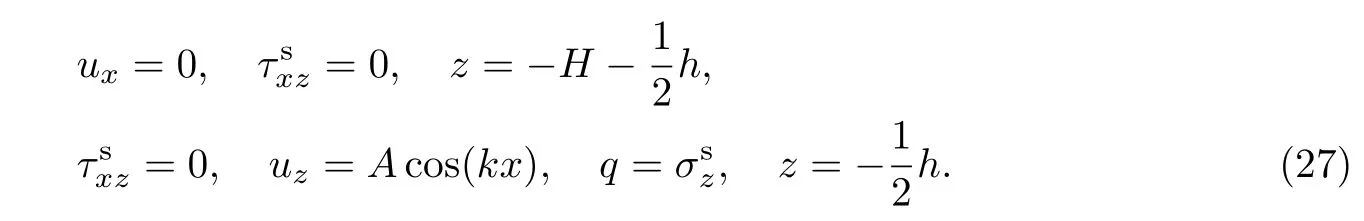
同樣,式(25)也成立.

聯立式(25)和(27),最終得到Winkler彈性系數為

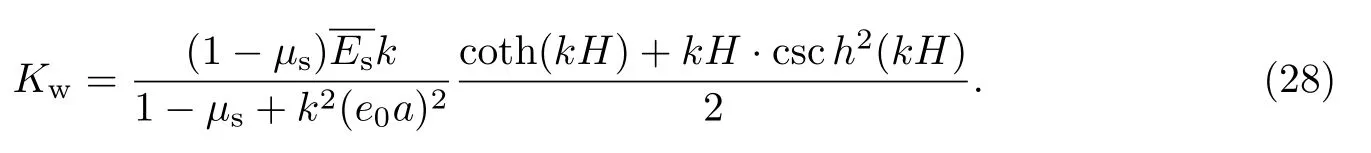
2 算例與討論

下面討論非局部理論下各種參數對系統屈曲行為的影響,首先引進如下無量綱參數:

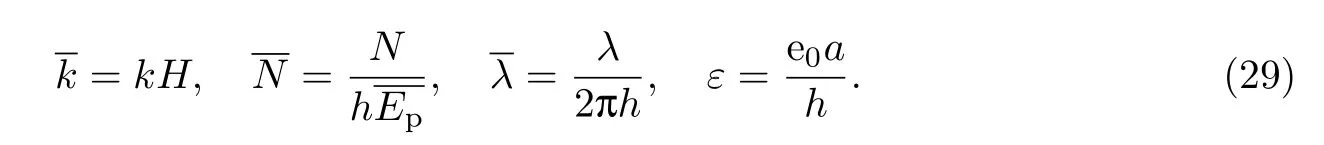
2.1 彈性基底的下表面

當彈性基地的下表面不同時,計算得到的Winkler彈性系數也不同,因此需要了解下界面條件對薄板起皺行為的影響.取薄板的厚度h=10 nm,彈性基底的泊松比μs=0.4,薄板與彈性基底的模量比=100,彈性基底與薄板的厚度比H/h=10,則可得到不同界面下非局部參數e0a對臨界載荷的影響,結果如圖3所示.

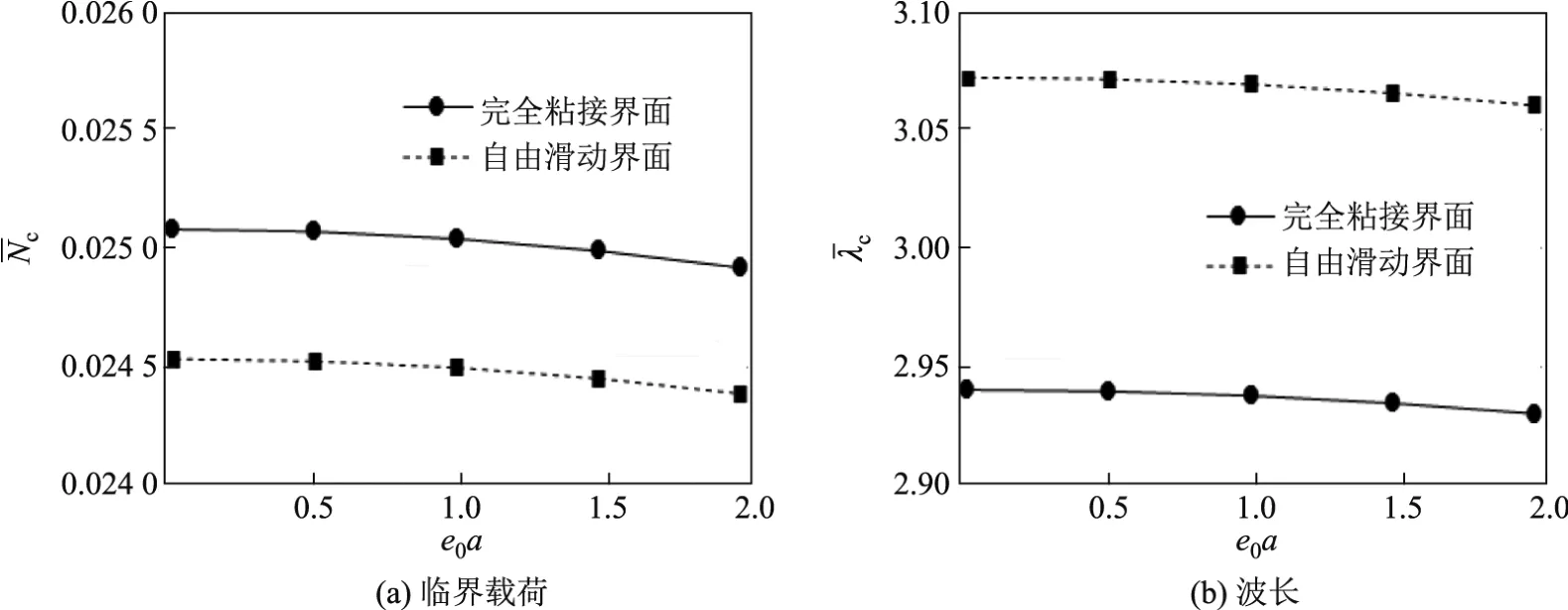
圖3 非局部參數對臨界載荷和波長的影響Fig.3 Eあects of nonlocal parameter on critical load and wavelength

由圖3可以看出:不論是完全粘接界面還是自由滑動界面,起皺載荷Nc和波長λc均隨著非局部參數e0a的增大而下降;與自由滑動界面相比,完全粘接界面下的臨界載荷Nc更大,而波長λc更小.

2.2 泊松比μs

彈性基底決定了Winkler彈性系數,因此彈性基底的泊松比影響薄板起皺行為.圖4為完全粘接界面下臨界載荷比和波長比關于泊松比μs的變化,其中為經典連續介質力學(非局部參數e0a=0)中對應的臨界載荷和波長.薄板的厚度h=10 nm,彈性模量比=100和厚度比H/h=10.

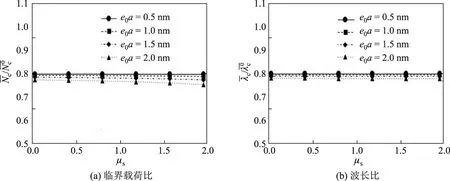
圖4 臨界載荷比和波長比關于泊松比的變化Fig.4 Curves of critical load ratio and wavelength ratio on Poission ratio

由圖4可以看出:非局部參數e0a越大,臨界載荷比隨著泊松比μs的增大而下降的趨勢越明顯;波長比隨著泊松比μs的變化基本不變.由此可見,引入非局部參數e0a后,薄板發生起皺時的臨界載荷對彈性基底的不可壓縮性變得敏感,而波長不受影響.

2.3 厚度比H/h

彈性基底和薄板的厚度比對Winkler彈性系數的影響較大,因此對薄板起皺行為也有影響.圖5為完全粘接界面下臨界載荷比和波長比關于厚度比H/h的變化,其中薄板的厚度h=10 nm,彈性基底的泊松比μs=0.4,彈性模量比=100.固定非局部參數e0a的情況下,臨界載荷比和波長比均隨著厚度比H/h的增大而增大,且趨于1.由此可見,彈性基底越薄,非局部效應越顯著.另外,彈性基底的厚度遠大于薄板時,非局部效應可忽略.

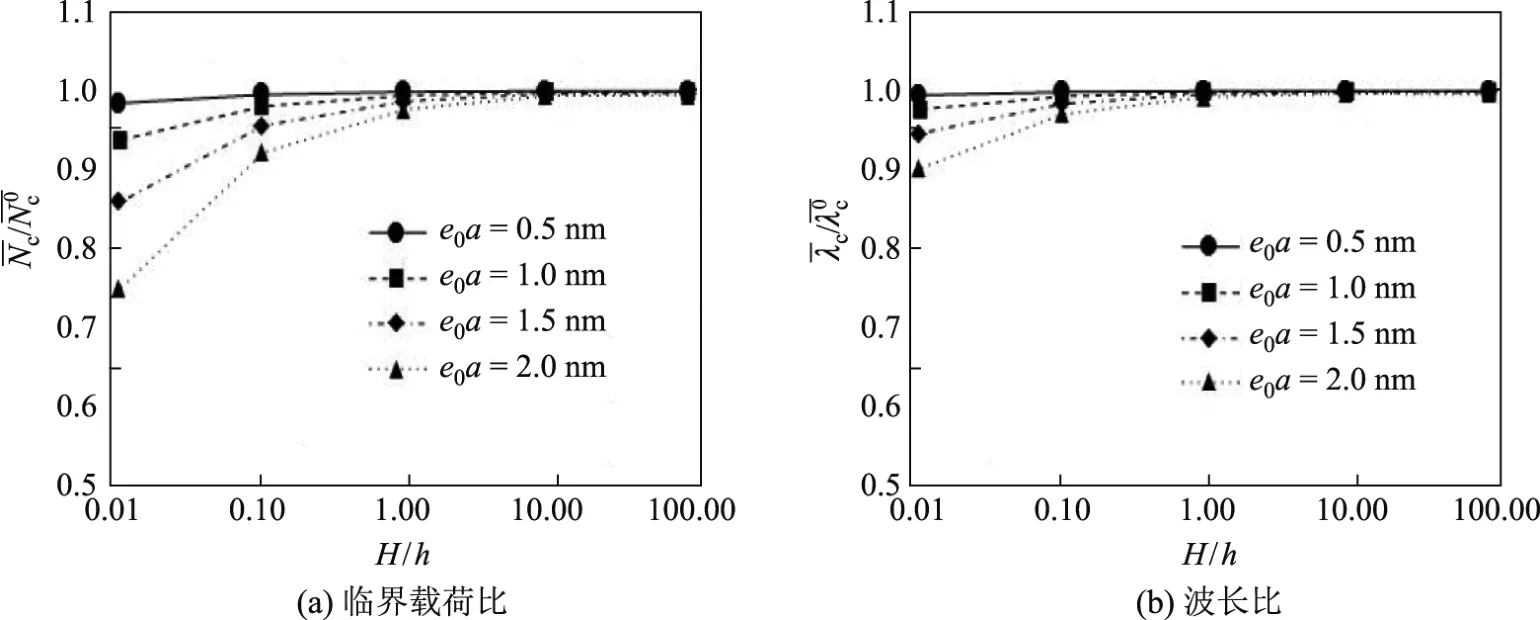
圖5 臨界載荷比和波長比關于厚度比的變化Fig.5 Curves of critical load ratio and wavelength ratio on thickness ratio

2.4 薄板與彈性基底的模量比

臨界載荷和波長的表達式中均含有表示薄板和彈性基底的模量比的變量,因此模量比對薄板的起皺行為有影響.圖6為完全粘接界面下臨界載荷比和波長比關于模量比的變化,其中薄板的厚度h=10 nm,彈性基底的泊松比μs=0.4,厚度比H/h=10.由圖6可以看出:隨著模量比的增大,臨界載荷比和波長比均增大,且趨于1;對于較小的模量比,非局部參數e0a越大,臨界載荷比和波長比的數值越小.因此,對于粘接在彈性基底的薄板系統,彈性基底的模量比薄板更大時,薄板的起皺行為具有顯著的非局部效應.

3 結束語

本工作基于非局部理論對彈性基底上粘接薄板的起皺問題進行了研究,分析了彈性基底的下表面、泊松比以及薄板與彈性基底的厚度比、模量比對薄板起皺行為的影響.研究結果表明,非局部參數的引入降低了薄板的有效抗彎剛度和彈性基底對薄板的法向作用,從而使得薄板發生起皺所需的載荷和起皺波長均減小.因此,對于厚軟的彈性基底,薄板系統的非局部效應可忽略.

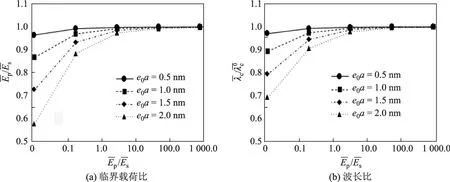
圖6 臨界載荷比和波長比關于楊模量比的變化Fig.6 Curves of critical load ratio and wavelength ratio on modulus ratio

[1]BOWDEN N,BRITTAIN S,EVANS A G,et al.Spontaneous formation of ordered structures in thin fi lms of metals supported on an elastomeric polymer[J].Nature,1998,393(6681):146-149.

[2]CHEN X,HUTCHINSON J W.A family of herringbone patterns in thin fi lms[J].Scripta Materialia,2004,50(6):797-801.

[3]ALLEN H G.Analysis and design of structural sandwich panels[M].Oxford:Pergamon Press Ltd,1969:38-132.

[4]CERDA E,MAHADEVAN L.Geometry and physics of wrinkling[J].Physical Review Letters,2003,90:074302.

[5]CHEN X,HUTCHINSON J W.Herringbone buckling patterns of compressed thin fi lms on compliant substrates[J].Journal of Applied Mechanics,2004,71(5):597-603.

[6]SONG J,JIANG H,CHOI W M,et al.An analytical study of two-dimensional buckling of thin if lms on compliant substrates[J].Journal of Applied Physics,2008,103(1):014303.

[7]HUANG Z Y,HONG W,SUO Z.Nonlinear analysis of wrinkles in a fi lm bonded to a compliant substrate[J].Journal of Mechanics and Physics of Solids,2005,53:2101-2118.

[8]LI B,HUANG S Q,FENG X Q.Buckling and postbuckling of a compressed thin fi lm bonded on a soft elastic layer:a three-dimensional analysis[J].Archive of Applied Mechanics,2010,80:175-188.

[9]ZHOU Y G,CHEN Y L,LIU B,et al.Mechanics of nanoscale wrinkling of graphene on a nondevelopable surface[J].Carbon,2015,84:263-271.

[10]YAkOBSON B I,BRABEC C J,BERNHOLC J.Nanomechanics of carbon tubes:instabilities beyond linear response[J].Physcial Review Letters,1996,76(14):2511-2514.

[11]ERINGEN A C.On diあerential equations of nonlocal elasticity and solutions of screw dislocation and surface waves[J].Journal of Applied Physics,1983,54(9):4703-4710.

[12]ERINGEN A C.Nonlocal continuum fi eld theories[M].New York:Springer-Verlag,2002:71-175.

[13]PRADHAN S C,PHADIkAR J K.Nonlocal elasticity theory for vibration of nanoplates[J].Journal of Sound and Vibration,2009,325(1/2):206-223.

[14]PRADHAN S C,MURMU T.Small scale eあect on the buckling analysis of single-layered graphene sheet embedded in an elastic medium based on nonlocal plate theory[J].Physica E:Lowdimensional Systems and Nanostructures,2010,42(5):1293-1301.

[15]BEHFAR K,NAGHDABADI R.Nanoscale vibrational analysis of a muti-layered grapheme sheet embedded in an elastic medium[J].Composites Science and Technology,2005,65(7/8):1159-1164.

[16]PENG X W,GUO X M,LIU L,et al.Scale eあects on nonlocal buckling analysis of bilayers composite plates under non-uniform loads[J].Applied Mathematics and Mechanics(English Edition),2015,36(1):1-10.

[17]劉亮,彭香武,王青占,等.粘接材料及結構在雙軸受壓和溫度耦合作用下變形的尺度效應和非局部效應分析[J].上海大學學報(自然科學版),2015,21(4):422-431.

[18]LIM C W.On the truth of nanoscale for nanobeams based on nonlocal elastic stress f i eld theory:equilibrium,governing equation and static def l ection[J].Applied Mathematics and Mechanics(English Edition),2010,31(1):37-54.

[19]吳連元.板殼穩定性理論[M].武漢:華中理工大學出版社,1996:19-68.

[20]黃義,何芳社.彈性地基上的梁、板、殼[M].北京:科學出版社,2005:49-74.

[21]徐芝綸.彈性力學簡明教程[M].3版.北京:高等教育出版社,2008:9-21.