基于降維觀測器的最優故障診斷算法研究

，,2,*，

1.北京控制工程研究所，北京 100190 2.北京空間飛行器總體設計部，北京 100094

近年來，面對航空航天等現代工業高可靠、長壽命的迫切需求，國內外關于故障診斷與重構技術的研究已經有了巨大發展[1-4]。憑借實時性高、對輸入信號要求較低等優點，基于觀測器的故障診斷算法得到了廣泛應用。從觀測器的設計原理來看，目前該類故障診斷算法主要有：未知輸入觀測器法(UIO)[5-6]、自適應觀測器法[7-8]以及H2/H∞魯棒觀測器法[9]等。而從觀測器的規模來看，該類故障診斷算法又可以分為：全維觀測器法和降維觀測器法。由于前者計算量大,響應速度慢，在系統較為復雜且實時性要求較高時，其實用性遠不如后者。然而，后者通常需要進行矩陣分塊運算，當系統規模較大時，該項工作十分繁瑣，會影響診斷算法的響應速度[10]。因此，有必要研究無需進行矩陣分塊運算的降維觀測器故障診斷算法。

另一方面，在診斷器設計過程當中，非常關鍵的一步就是觀測器增益的選取問題，現有文獻多采用各類不等式進行求解[7-8]，由此來保證診斷結果的收斂性。然而，收斂并不代表診斷結果最優。文獻[11-12]基于對偶原理，證明了某系統的(最優)觀測器設計問題可以轉換為對偶系統的(最優)控制器設計問題。在上述結論的指導下，可以進一步確定診斷算法的最優增益。

此外，實際工程應用當中，常常會遇到這樣一種情況：雖然不知道真實的故障何時發生、發生時幅值為多大，但知道故障的類型，對其變化特性具有一定的認知。換言之，這類故障的動態特性是已知的，而具體發生時刻與初始狀態未知，需進行診斷辨識得到。

因此，本文針對一類動態特性已知的快變偏差故障，利用正交原理和對偶原理，設計了一種無需進行矩陣分塊運算且增益最優的基于降維觀測器的故障診斷算法，實現了對故障的最小方差估計。在此基礎之上，利用診斷結果對故障系統進行了控制重構。最后，通過數值仿真，驗證了所提方法的有效性。

1 問題描述

假設m個執行器中有mk個受故障影響，考慮如下故障系統模型：

式中：x∈Rn、u∈Rm、y∈Rq分別為系統的狀態向量、控制輸入向量及輸出向量；A、B、C為相應維度的常量矩陣；fa∈Rmk為執行機構的故障信號，不可直接測量，fai是fa的第i個分量；bi代表B的第i列，Fa是故障執行機構對應的編號集，F∈Rn×mk由故障執行機構編號對應的bi順序組合而成，即F=[bi],i∈Fa。

這里借鑒文獻[13-14]中的故障模型描述方法，利用一個“外系統”來描述動態特性已知的故障fa，具體表示如下：

式中：xfa∈Rr是執行機構故障的狀態向量。Afa和Cfa是適當維數的常量矩陣。故障的發生時刻tf和初始狀態xfa0是未知的。

上述故障描述方法可用于正弦曲線型故障、斜坡型故障、階躍型故障、發散型故障、收斂型故障以及其他更一般的持續型故障，具有廣泛的適用性。

2 故障診斷與重構

2.1 故障診斷

下面設計一種基于降維擴展狀態觀測器的故障診斷算法。

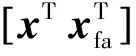
(3)

令W11∈Rn×q,W21∈Rr×q,W12∈Rn×(n+r-q)，W22∈Rr×(n+r-q)，構造如下降階觀測器，即故障診斷器：

設觀測誤差為：

代入式(4)和式(5)，可得觀測誤差方程為：

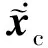
文獻[11-12]基于對偶原理，論證了(最優)觀測器的設計問題可以轉換為對偶系統的(最優)控制器設計問題。

式(7)誤差方程的對偶系統為：

設：

它可以視為對偶系統的等效控制輸入，其中LT為等效狀態反饋增益，則式(8)閉環系統等價于：

文獻[12]證明了待觀測狀態的線性加權Txc(t)的估計方差可轉化成如下形式的積分二次型函數：

J=ψT(t0)S0ψ(t0)+

式中：S0,S∈R(n+r-q)×(n+r-q)和R∈Rq×q分別是正定和半正定矩陣。

(12)

由最優控制理論，可以求得式(10)系統在式(12)二次性能指標下的最優控制律為：

式中：H是下列Riccati矩陣方程的唯一正定解：

對比式(13)和式(9)，可得最優故障診斷器的狀態反饋增益矩陣L為：

2.2 控制重構

基于上述故障診斷結果，可以設計重構控制器，以實現系統與故障的隔離。

假設標稱模型的控制目標是：在規定任務時間tmis內，使系統跟蹤到期望模型：

在已經診斷出故障的前提下，設計相應的容錯控制律ur(t)以隔離故障。可采用故障補償的思想，在標稱控制律un(t)的基礎之上附加故障補償項uξ(t)，即：

這里不妨采用狀態反饋控制器作為標稱控制器，即un(t)=-Kx(t)。其中，反饋增益K滿足：

以一般的偽逆法為例，反饋增益K可取為：

由于F=[bi],i∈Fa，所以存在一個矩陣Ma，使得F=BMa，因此uξ(t)可以設計為：

通過上述故障診斷器和重構控制器的構建，實現了故障系統的主動容錯控制。

3 數值仿真驗證

為了驗證上述診斷算法的有效性，這里采用文獻[15]的算例，進行數值仿真驗證。

考慮式(1)描述的含加性時變故障的線性定常系統，其中的矩陣參數及初始狀態如下：

式(2)描述的故障模型參數矩陣如下：

式(16)所示期望模型的系統矩陣為：

取故障發生時刻為：tf=25 s。

預定任務完成時間為：tmis=100 s。

根據(15)求得故障診斷器的增益矩陣L為：

在以上的參數條件下，仿真結果如圖1～圖7所示。

由圖1、圖2可知，系統在25 s時發生周期性時變故障，故障后系統輸出周期性振蕩，不再收斂為零。

通過對系統輸入輸出的測量，最優故障診斷器得到的故障診斷值和真實值如圖3所示，診斷誤差如圖4所示，可見該故障診斷器可在7 s內快速收斂到真實值，由此驗證了診斷器的有效性。

假設系統發生故障后立即進行控制重構，即tr=tf=25 s，得到重構后的系統響應曲線如圖5所示，可見系統輸出在重構控制器的作用下能夠重新收斂于期望值，由此驗證了重構控制器的有效性。

圖6、圖7為分別在tr1=25 s、tr2=31 s進行控制器重構的系統輸入輸出響應曲線。結果顯示：雖然盡早地采取重構措施，會降低系統偏差，但需要以更大的控制輸入為代價，因此重構時刻并非越快越好，需要折衷考慮狀態偏差與重構代價等多重因素。

4 結束語

本文利用正交原理和對偶原理，設計了一種基于降維觀測器的最優故障診斷算法，在此基礎之上實現了對故障系統的控制重構。該算法具有如下優點：

1)無需進行矩陣分塊運算即可對診斷器進行降維，降低了計算的復雜性；

2)通過求解對偶系統的最優控制律，即可確定診斷算法的最優增益，從而實現對故障的最小方差估計。

最后，通過數值仿真，得到以下結論：

1)本文所提最優降維故障診斷算法能夠快速有效地估計出系統故障，給出故障初值與發生時刻；

2)對系統進行控制重構并非越早越好，因為盡早重構雖然會降低系統偏差，但需要以更大的控制輸入為代價。

References)

[1] 顧朋, 王大軼, 劉成瑞.零動量輪衛星控制系統可重構性設計研究[J]. 中國空間科學技術, 2013,33(1): 7-14.

GU P， WANG D Y, LIU C R. Research on momentum wheel reconfiguration design of zero-momentum satellite[J]. Chinese Space Science and Technology, 2013,33(1): 7-14(in Chinese).

[2] 胡宇桑, 王大軼, 劉成瑞. 基于能耗與可靠性約束的動量輪可重構性評價[J]. 中國空間科學技術, 2014, 34(5): 10-17.

HU Y S, WANG D Y, LIU C R. Reconfigurability evaluation of momentum wheel control system under energy and reliability constraints[J]. Chinese Space Science and Technology, 2014, 34(5):10-17(in Chinese).

[3] 李文博，王大軼，劉成瑞. 動態系統實際故障可診斷性的量化評價研究[J]. 自動化學報, 2014, 41(3):497-507.

LI W B, WANG D Y, LIU C R. Quantitative evaluation of actual fault diagnosability for dynamic systems[J]. Acta Automatica Sinica, 2014, 41(3):497-507(in Chinese).

[4] YIN S, XIAO B, DING S X, et al. A review on recent development of spacecraft attitude fault tolerant control system[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3311-3320.

[5] HAMDAOUI R, ABDELKRIM M N. Timely actuator fault diagnosis and accommodation[C]∥International Multi-conference on System, Signals & Devices. Hammamet: IEEE, 2013: 1-8.

[6] HAMDAOUI R, GUESMI S, EI HARABI R. UIO based robust fault detection and estimation[C]∥Proceedings of International Conference on Control.Strbske Pleso, Slovakia,2013: 076-081.

[7] ZHANG K, JIANG B, COCQUEMPOT V. Adaptive observer-based fast fault estimation[J]. International Journal of Control Automation & Systems, 2008, 6(3): 320-326.

[8] JIANG B, STAROSWIECKI M. Adaptive observer design for robust fault estimation[J]. International Journal of Systems Science, 2010, 33(33): 767-775.

[9] COLLINS E G, SONG T. ROBUST H∞ estimation and fault detection of uncertain dynamic systems[J]. Journal of Guidance Control & Dynamics, 2000, 23(5): 857-864.

[10] TANG G Y, LI J. Optimal fault diagnosis for systems with delayed measurements[J]．IET Control Theory & Applications, 2008, 2(11): 990-998.

[11] 韓京清. 線性控制系統的對偶性[J]. 數學年刊:中文版, 1980(1): 31-39.

[12] 言茂松. 最佳控制與觀測(五)[J]. 電氣傳動, 1979(3): 53-70.

[13] JOSHI S M, GONZLEZ O R, UPCHURCH J M. Identifiability of additive, time-varying actuator and sensor faults by state augmentation,NASA/TM-2014-218669[R].Washington DC:NASA, 2014.

[14] JOSHI SM, GONZLEZ O R, UPCHURCH J M. Identifiability of additive actuator and sensor faults by state augmentation[J]. Journal of Guidance Control & Dynamics,2014, 37(3): 941-946.

[15] TANG G Y, LI J. Optimal fault diagnosis for systems with delayed measurements[J]. Iet Control Theory & Applications, 2008, 2(11): 990-998.