基于容積變換的平滑變結(jié)構(gòu)濾波及應(yīng)用

林孝工, 焦玉召, 李 恒, 梁 坤, 聶 君

(哈爾濱工程大學(xué)自動(dòng)化學(xué)院, 黑龍江 哈爾濱 150001)

0 引 言

隨著對(duì)海洋資源的探索,船舶動(dòng)力定位技術(shù)也得到了更多關(guān)注[1-2]。對(duì)可微非線性系統(tǒng),將非線性系統(tǒng)模型展開(kāi)為關(guān)于均值的泰勒多項(xiàng)式,僅保留線性部分,即得擴(kuò)展卡爾曼濾波(extended Kalman filter,EKF)[3]算法。EKF需計(jì)算Jacoby矩陣,且有高階截?cái)嗾`差。因而對(duì)強(qiáng)非線性系統(tǒng),可能會(huì)出現(xiàn)估計(jì)誤差較大或者無(wú)法收斂的情況。此時(shí)可計(jì)算Jacoby和Hessian矩陣得到二階擴(kuò)展卡爾曼濾波(second-order extended Kalman filter,SOEKF)[4],但計(jì)算量大。非線性濾波的另一種策略是基于Sigma點(diǎn)的無(wú)跡卡爾曼濾波(unscented Kalman filter,UKF)[5],UKF不需要Jacoby矩陣。同時(shí)基于球面徑向容積規(guī)則,得到容積卡爾曼濾波(cubature Kalman filter,CKF)[6]。且這些非線性狀態(tài)估計(jì)方法,已廣泛應(yīng)用于慣性導(dǎo)航[7]、狀態(tài)估計(jì)[8]等。同時(shí)通過(guò)平方根因子傳遞,可保證算法的數(shù)值穩(wěn)定性[9-10]。

模型精確時(shí),基于Kalman的濾波器具有較高估計(jì)精度,然而模型參數(shù)不確定或噪聲干擾的隨機(jī)性,傳統(tǒng)算法可能會(huì)發(fā)散[11]。故文獻(xiàn)[12]將滑模概念引入濾波增益的計(jì)算中,提出變結(jié)構(gòu)濾波(variable structure filter,VSF)。VSF是一種基于不確定模型的濾波算法,通過(guò)引入平滑邊界層,得到具有固定平滑邊界層的平滑變結(jié)構(gòu)濾波[13]。實(shí)際系統(tǒng)干擾和不確定性具有隨機(jī)性,令估計(jì)誤差協(xié)方差對(duì)平滑邊界層求偏導(dǎo),可得近似最優(yōu)平滑邊界層[14]。文獻(xiàn)[15]將邊界層擴(kuò)展為全矩陣形式,得到具有最優(yōu)平滑邊界層的平滑變結(jié)構(gòu)濾波(smoothing variable structure filter,SVSF)算法。

模型不確定時(shí),SVSF是一種有效的濾波算法[16-17]。但仍具有一定局限性:①要求系統(tǒng)方程是適度非線性且可微,需計(jì)算系統(tǒng)的Jacoby矩陣;②受計(jì)算機(jī)字長(zhǎng)限制,誤差積累可能使協(xié)方差失去非負(fù)定性,導(dǎo)致濾波發(fā)散。為解決這兩個(gè)問(wèn)題,一方面將CKF與具有最優(yōu)平滑邊界層的SVSF算法相結(jié)合,利用容積規(guī)則計(jì)算狀態(tài)預(yù)測(cè)值、狀態(tài)協(xié)方差預(yù)測(cè)、測(cè)量預(yù)測(cè)值和測(cè)量協(xié)方差預(yù)測(cè)值,得到了基于容積規(guī)則的平滑變結(jié)構(gòu)濾波(cubature-smoothing variable structure filter,C-SVSF)算法,既提高了SVSF算法的估計(jì)精度,又?jǐn)U展了SVSF算法的應(yīng)用范圍。另一方面,通過(guò)在狀態(tài)傳遞過(guò)程中使用協(xié)方差的平方根因子,保證協(xié)方差的正定性和對(duì)稱(chēng)性,得到平方根容積平滑變結(jié)構(gòu)濾波(square root cubature-smoothing variable structure filter,SRC-SVSF),SRC-SVSF是具有數(shù)值穩(wěn)定性的濾波算法。

1 基于Jacoby的SVSF

考慮非線性系統(tǒng):

xk=fk-1(xk-1)+ωk

(1)

zk=hk(xk)+υk

(2)

式中,fk-1(·)和hk(·)表示狀態(tài)方程和測(cè)量方程;xk是狀態(tài)矢量;zk是觀測(cè)值;ωk和υk是狀態(tài)噪聲和觀測(cè)噪聲,服從高斯分布ωk～N(q,Q),υk～N(r,R),其中q和r是均值,Q和R是方差。

假設(shè)1假設(shè)系統(tǒng)式(1)和式(2)滿(mǎn)足文獻(xiàn)[13]中的定義,即不考慮測(cè)量噪聲時(shí),系統(tǒng)xk=fk-1(xk-1)和zk=hk(xk)是連續(xù)的雙射或是完全可觀和完全可控的,即通過(guò)觀測(cè)矢量zk存在一個(gè)逆映射能唯一的得到狀態(tài)矢量xk,即

(3)

如果系統(tǒng)式(1)、式(2)轉(zhuǎn)換矩陣fk和hk是常系數(shù),那么直接得卡爾曼濾波器。如果轉(zhuǎn)換矩陣是非線性的,那么可通過(guò)計(jì)算Jacoby矩陣得EKF算法。

對(duì)模型不精確系統(tǒng),EKF誤差較大,而SVSF可有效抑制模型不精確帶來(lái)的濾波發(fā)散。原理如圖1所示,當(dāng)預(yù)測(cè)值超出存在的子空間時(shí),說(shuō)明有不確定干擾,可通過(guò)不連續(xù)增益將估計(jì)值矯正到真實(shí)值附近,保證算法對(duì)不確定干擾的魯棒性。

圖1 SVSF算法概念圖Fig.1 Concept of SVSF

同時(shí),為消除不連續(xù)增益的頻繁切換造成的系統(tǒng)顫動(dòng),文獻(xiàn)[13]引入固定平滑邊界層。假設(shè)系統(tǒng)存在有界隨機(jī)干擾,那么令平滑邊界層等于該干擾的保守上界。通過(guò)引入飽和函數(shù)式(4),當(dāng)估計(jì)誤差大于邊界層時(shí),用不連續(xù)增益來(lái)保證算法穩(wěn)定運(yùn)行;當(dāng)誤差在邊界層內(nèi)時(shí),用連續(xù)增益進(jìn)行狀態(tài)估計(jì),進(jìn)而消除一定的顫動(dòng)影響。

(4)

圖2 具有邊界層的SVSFFig.2 SVSF with smooth boundary layer

實(shí)際中該上界不容易獲得,文獻(xiàn)[14-15]提出具有協(xié)方差導(dǎo)引的平滑變結(jié)構(gòu)濾波算法。基于狀態(tài)估計(jì)誤差協(xié)方差最小原則得到具有最優(yōu)平滑邊界層的SVSF。狀態(tài)預(yù)測(cè)值和測(cè)量估計(jì)值分別為

(5)

(6)

(7)

狀態(tài)預(yù)測(cè)誤差協(xié)方差為

(8)

測(cè)量預(yù)測(cè)值為

(9)

新息ez,k+1|k和測(cè)量估計(jì)誤差ez,k+1|k+1為

(10)

(11)

基于新息和測(cè)量誤差,得增益[15]為

?

(12)

進(jìn)而,可得狀態(tài)估計(jì)更新值為

(13)

估計(jì)誤差協(xié)方差更新值為

(14)

(15)

式(5)～式(14)即是變結(jié)構(gòu)濾波算法。下面通過(guò)引理1進(jìn)一步證明算法的穩(wěn)定性問(wèn)題。

引理1若估計(jì)誤差滿(mǎn)足式(16),則狀態(tài)估計(jì)過(guò)程是穩(wěn)定和收斂的[13]。

|ek|<|ek-1|

(16)

因而,只需證明狀態(tài)估計(jì)誤差滿(mǎn)足引理1,就可證明出狀態(tài)估計(jì)過(guò)程是穩(wěn)定和收斂的。

定理1若系統(tǒng)滿(mǎn)足假設(shè)1,狀態(tài)增益滿(mǎn)足不等式,那么濾波算法是穩(wěn)定和收斂的。

|ez,k+1|k|<|Hk+1Kk+1ez,k+1|k|<|ez,k+1|k|+|ez,k|k|

(17)

sign(Hk+1Kk+1ez,k+1|k)=sign(ez,k+1|k)

(18)

證明由不等式(17)可知,|Hk+1Kk+1ez,k+1|k|-|ez,k+1|k|<|ez,k|k|成立,又由于Hk+1Kk+1ez,k+1|k與ez,k+1|k同號(hào),那么可得,|ez,k+1|k-Hk+1Kk+1ez,k+1|k|<|ez,k|k|。結(jié)合式(6)和式(9)～式(13),得ez,k+1|k-Hk+1Kk+1ez,k+1|k=ez,k+1|k+1。則不等式|ez,k+1|k+1|<|ez,k|k|成立。又由于系統(tǒng)是完全可觀和可控的,因而知|ex,k+1|k+1|<|ex,k|k|成立,滿(mǎn)足引理1,故估計(jì)算法是穩(wěn)定和收斂的。

證畢

由上可知,對(duì)于完全可觀和完全可控的系統(tǒng),狀態(tài)估計(jì)誤差具有穩(wěn)定性和收斂性的充分條件是輸出估計(jì)誤差是穩(wěn)定和收斂的。因而,由定理1,令增益為

(19)

綜上,SVSF對(duì)不確定非線性系統(tǒng)具有一定的魯棒性,但是仍無(wú)法克服EKF算法的局限性。針對(duì)此,一種直接的思路是通過(guò)容積變換來(lái)代替非線性系統(tǒng)的線性化,得到CKF算法。CKF由于不需要計(jì)算Jacoby矩陣,同時(shí)簡(jiǎn)化了計(jì)算,因而得到了廣泛的應(yīng)用。

2 基于容積變換的非線性濾波策略

2.1 CKF算法

(20)

狀態(tài)預(yù)測(cè)值和協(xié)方差預(yù)測(cè)值為

(21)

(22)

測(cè)量預(yù)測(cè)值和新息協(xié)方差為

(23)

(24)

估計(jì)誤差互協(xié)方差為

(25)

以上即是CKF的狀態(tài)和協(xié)方差預(yù)測(cè)方程。

2.2 C-SVSF算法

基于以上描述,CKF預(yù)測(cè)方程可有效克服EKF的缺點(diǎn)。因而本文考慮采用容積規(guī)則來(lái)計(jì)算SVSF的狀態(tài)預(yù)測(cè)和協(xié)方差預(yù)測(cè)值,從而得到C-SVSF算法。C-SVSF不僅保持了SVSF算法的魯棒性,而且不需要計(jì)算系統(tǒng)的Jacoby矩陣,因而估計(jì)精度將高于SVSF算法。C-SVSF算法流程如下。

步驟1狀態(tài)預(yù)測(cè)式(5)和協(xié)方差預(yù)測(cè)式(8)分別變?yōu)槭?21)和式(22)。從而得到基于容積規(guī)則的狀態(tài)預(yù)測(cè)和協(xié)方差預(yù)測(cè)值。

步驟2上一時(shí)刻的測(cè)量估計(jì)誤差ez,k-1|k-1

首先，計(jì)算觀測(cè)方程的傳遞容積點(diǎn)為

(26)

(27)

則測(cè)量估計(jì)誤差為

(28)

以上即是C-SVSF算法,克服了非線性系統(tǒng)式(1)必須連續(xù)可微的條件,且不需要計(jì)算系統(tǒng)的Jacoby矩陣,即保持了SVSF的魯棒性,又由于容積規(guī)則的引入使得狀態(tài)預(yù)測(cè)和協(xié)方差預(yù)測(cè)的精度得到了進(jìn)一步提高。因而得到的C-SVSF算法估計(jì)精度理論上要高于基于Jacoby矩陣的擴(kuò)展平滑變結(jié)構(gòu)濾波(extended-SVSF,E-SVSF)算法。同時(shí)與標(biāo)準(zhǔn)E-SVSF算法具有相同的濾波框架,因而仍是一種穩(wěn)定的濾波算法。

與CKF相似,C-SVSF在最優(yōu)邊界層計(jì)算中要求計(jì)算協(xié)方差的逆矩陣,因而協(xié)方差矩陣需要滿(mǎn)足非負(fù)定性的要求。然而由于計(jì)算機(jī)字長(zhǎng)限制或者誤差的累計(jì)可能會(huì)使協(xié)方差失去非負(fù)定性,從而導(dǎo)致算法數(shù)值發(fā)散。因而,為了提高C-SVSF算法的數(shù)值穩(wěn)定性,類(lèi)似于平方根容積卡爾曼濾波算法[6],由下三角分解的方法給出了SRC-SVSF算法。

2.3 SRC-SVSF算法

(29)

式中

步驟3新息協(xié)方差平方根因子為

(30)

步驟5估計(jì)誤差協(xié)方差平方根因子更新公式為

(31)

綜上,將容積卡爾曼濾波策略中計(jì)算狀態(tài)和協(xié)方差預(yù)測(cè)的方法引入到SVSF算法中,得到的C-SVSF由于不需要計(jì)算非線性系統(tǒng)式的Jacoby矩陣,因而其估計(jì)精度要高于E-SVSF算法,且SRC-SVSF保障了算法的數(shù)值穩(wěn)定性。

3 仿真實(shí)驗(yàn)及分析

建立三自由度船舶運(yùn)動(dòng)方程[2]為

(32)

三自由度觀測(cè)方程為

zk+1=hk(xk)+υk

(33)

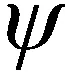
對(duì)非線性動(dòng)力定位船舶位置估計(jì)系統(tǒng),CKF算法的估計(jì)精度要高于EKF算法的估計(jì)精度。因而以CKF作為對(duì)比算法，分別在觀測(cè)噪聲協(xié)方差已知和未知兩種情況下,與E-SVSF、C-SVSF和SRC-SVSF算法進(jìn)行仿真對(duì)比。

3.1 觀測(cè)噪聲協(xié)方差精確已知

假設(shè)測(cè)量噪聲協(xié)方差是精確已知的,即R=diag([20,20,20,20,20,20])。采樣周期1 s,采樣時(shí)間1 800 s。通過(guò)200次蒙特卡羅仿真實(shí)驗(yàn),4種算法下船舶位置和速度RMSE分別如圖3和圖4所示。

圖3 已知噪聲下的北-東-艏向位置RMSEFig.3 RMSE of north-east-head with known noise

圖4 已知噪聲下的縱蕩-橫蕩-艏搖RMSEFig.4 RMSE of surge-sway-yaw with known noise

由于在噪聲已知時(shí),CKF是最優(yōu)狀態(tài)估計(jì)算法,故CKF具有最小RMSE。由于狀態(tài)和協(xié)方差預(yù)測(cè)引入了Jacoby矩陣,因而E-SVSF誤差最大。同時(shí),容積規(guī)則的引入使C-SVSF算法精度高于E-SVSF。而SRC-SVSF算法由于狀態(tài)傳遞過(guò)程中使用協(xié)方差的平方根因子,因而與C-SVSF具有幾乎相同的估計(jì)誤差。表1是狀態(tài)在不同算法下的平均RMSE。可知C-SVSF及其平方根形式SRC-SVSF具有相同估計(jì)誤差,且都高于E-SVSF,說(shuō)明了改進(jìn)算法的有效性。

表1 已知噪聲下算法的平均RMSE

3.2 觀測(cè)噪聲協(xié)方差未知

假設(shè)測(cè)量噪聲協(xié)方差未知,即可令R=diag([500,500,1 000,1 000,1 000,1 000])。采樣周期仍為1 s,采樣時(shí)間1 800 s。通過(guò)200次蒙特卡羅仿真實(shí)驗(yàn),可得此時(shí)船舶位置和速度RMSE分別如圖5和圖6所示。可知當(dāng)測(cè)量噪聲協(xié)方差未知時(shí),由于CKF算法不具有魯棒性,因而CKF估計(jì)誤差最大。而基于SVSF的濾波算法對(duì)不確定干擾具有一定的魯棒性,因而估計(jì)精度高于CKF算法。同時(shí)由于容積規(guī)則的引入,C-SVSF和SRC-SVSF算法的估計(jì)精度要高于E-SVSF算法,這與理論分析相一致。同時(shí)，表2給出了測(cè)量噪聲協(xié)方差未知時(shí),4種算法下的平均RMSE。

圖5 未知噪聲下的北-東-艏向RMSEFig.5 RMSE of north-east-head with unknown noise

圖6 未知噪聲下的縱蕩-橫蕩-艏搖RMSEFig.6 RMSE of surge-sway-yaw with unknown noise

算法參數(shù)x′/my′/m/(°)u/(m/s)v/(m/s)r/((°)/s)CKF6．676．668．325．785．785．39E?SVSF4．224．227．044．954．954．12C?SVSF4．124．123．894．594．613．65SRC?SVSF4．124．123．894．594．613．65

綜上可知:測(cè)量噪聲協(xié)方差已知時(shí),C-SVSF、SRC-SVSF與CKF具有相近估計(jì)精度,且都高于E-SVSF的估計(jì)精度;當(dāng)測(cè)量噪聲協(xié)方差未知時(shí),C-SVSF、SRC-SVSF具有相似估計(jì)精度,且高于E-SVSF,同時(shí)由于SVSF對(duì)噪聲干擾的魯棒性,因而精度均高于CKF。進(jìn)一步說(shuō)明本文C-SVSF和SRC-SVSF算法的有效性以及存在噪聲干擾時(shí)算法的魯棒性。

4 結(jié) 論

本文提出了C-SVSF算法,該算法既能消除Jacoby矩陣計(jì)算,又能充分利用SVSF的魯棒性;為保證算法的數(shù)值穩(wěn)定性,給出SRC-SVSF算法。由仿真知,當(dāng)測(cè)量噪聲協(xié)方差已知,C-SVSF、SRC-SVSF與CKF具有相似估計(jì)精度且高于E-SVSF;當(dāng)測(cè)量噪聲協(xié)方差未知,C-SVSF、SRC-SVSF估計(jì)精度仍高于E-SVSF,同時(shí)由于SVSF的魯棒性,基于SVSF的估計(jì)精度均高于CKF,進(jìn)一步說(shuō)明所提算法的優(yōu)越性。因而,C-SVSF和SRC-SVSF可以作為船舶狀態(tài)估計(jì)器使用,且當(dāng)測(cè)量噪聲協(xié)方差未知時(shí),可以替代已有的E-SVSF或CKF進(jìn)行狀態(tài)估計(jì)。

[1] 邊信黔, 付明玉, 王元慧. 船舶動(dòng)力定位[M]. 北京:科學(xué)出版社, 2011.

BIAN X Q, FU M Y, WANG Y H. Ship dynamic positioning[M]. Beijing: Science Publishing Company, 2011.

[2] 徐樹(shù)生. 船舶動(dòng)力定位系統(tǒng)多傳感器信息融合方法研究[D]. 哈爾濱: 哈爾濱工程大學(xué), 2013.

XU S S. Research on the multi-sensor information fusion methods of vessel dynamic positioning system[D]. Harbin: Harbin Engineering University, 2013.

[3] HAUG A J. Bayesian estimation and tracking: a practical guide[M]. New Jersey: Wiley, 2012.

[4] MAHALANABIS A K, FAROOQ M. A second-order method for state estimation of non-linear dynamical systems[J]. International Journal of Control, 1971, 14(4):631-639.

[5] QUINE B, UHLMANN J, DURRANTWHYTE H. Implicit Jacobians for linearised state estimation in nonlinear systems[C]∥Proc.of the American Control Conference, 1995:1645-1646.

[6] ARASARATNAM I, HAYKIN S. Cubature Kalman filters[J]. IEEE Trans.on Automatic Control, 2009, 54(6):1254-1269.

[7] LIU M, LAI J, LI Z, et al. An adaptive cubature Kalman filter algorithm for inertial and land-based navigation system[J]. Aerospace Science & Technology, 2016, 51(2):52-60.

[8] LIN C, GONG X, XIONG R, et al. A novelH∞, and EKF joint estimation method for determining the center of gravity position of electric vehicles[J].Applied Energy,2017,194:609-616.

[9] 徐樹(shù)生, 林孝工, 趙大威. 強(qiáng)跟蹤SRCKF及其在船舶動(dòng)力定位中的應(yīng)用[J]. 儀器儀表學(xué)報(bào), 2013, 34(6):1266-1272.

XU S S, LIN X G, ZHAO D W. Strong tracking SRCKF and its application in vessel dynamic positioning[J]. Chinese Journal of Scientific Instrument, 2013, 34(6): 1266-1272.

[10] 付夢(mèng)印. Kalman濾波理論及其在導(dǎo)航系統(tǒng)中的應(yīng)用[M]. 北京:科學(xué)出版社, 2010.

FU M Y. Kalman filtering theory and its application in navigation system[M]. Beijing: Science Publishing Company, 2010.

[11] TIAN T, SUN S, LI N. Multi-sensor information fusion estimators for stochastic uncertain systems with correlated noises[J]. Information Fusion, 2016, 27(C):126-137.

[12] HABIBI S R, BURTON R, HABIBI S R, et al. The variable structure filter[J]. Journal of Dynamic Systems Measurement & Control, 2002, 125(3):157-165.

[13] HABIBI S. The smooth variable structure filter[J]. Proceedings of the IEEE, 2007, 95(5):1026-1059.

[14] GADSDEN S A, EL SAYED M, HABIBI S R. Derivation of an optimal boundary layer width for the smooth variable structure filter[C]∥Proc.of the American Control Conference, 2011:4922-4927.

[15] GADSDEN S A, HABIBI S R. A new robust filtering strategy for linear systems[J]. Journal of Dynamic Systems Measurement & Control, 2012, 135(1):359-370.

[16] ATTARI M, GADSDEN S A, HABIBI S. Target tracking formulation of the SVSF with data association techniques[J]. IEEE Trans.on Aerospace & Electronic Systems, 2017, 53(1):12-25.

[17] ATTARI M, LUO Z, HABIBI S. An SVSF-based generalized robust strategy for target tracking in clutter[J]. IEEE Trans.on Intelligent Transportation Systems, 2016, 17(5):1381-1392.