基于脆性指標與物元理論的可爆性分級技術與應用

嚴榮富，黃溫鋼，王清亞，杜 勛

(1.東華理工大學核資源與環境國家重點實驗室培育基地，江西 南昌 330013；2.東華理工大學地球科學學院，江西 南昌 330013)

0 引言

爆破是礦山生產過程中的一項重要工作，爆破巖石或者礦石數量的多少和質量的好壞，無不影響著后續的裝載、運輸、破碎的效率。某礦在露天轉地下的過程中，爆破參數不因礦巖種類變化而做出調整，套用一種設計方案，造成礦巖爆破單耗過高，崩落礦石破碎情況不一，出礦量一直處于偏緊的結果，不能有效滿足選場的生產需求。為緩解矛盾，亟需對礦巖的可爆性進行分級研究，以提高爆破的效率，緩解采掘銜接矛盾。

礦巖的可爆性是對巖體抵抗爆破難易程度的描述，它取決于巖石自身的物理力學性質，是對巖石爆破參數進行優化，改善爆破效果的基礎。要做好礦山的爆破工作，必須要建立對礦巖可爆性的定性尤其是定量標準，即礦巖的可爆性分級。目前，國內外高校和科研單位對巖體可爆性分級提出了很多方法。根據分級準則的不同，提出主要有以巖石強度(抗壓、抗拉、抗剪)、炸藥單位消耗量、工程地質參數(節理、裂隙等)、巖石彈性波速度、巖石波阻抗或巖石爆破能量等作為分級指標,并引入了統計數學、模糊數學中的許多方法，如灰色關聯度可爆性分級[1]、人工神經網絡可爆性分級[2]、遺傳程序設計可爆性分級[3]和模糊聚類分析[4]等進行可爆性分級的評價，均取得了較好的結果。但也反映出可爆破性分級的復雜性，評價指標的多樣性及不確定性等問題。物元理論，通過隸屬函數對物元量值規格化，能夠更好地解決這類多屬性、不相容、定性與定量的綜合評價問題[5]。本文引入基于博弈論的改進物元可拓方法[6]，將主觀權重與客觀權重進行優化結合，對待評物元進行綜合賦權，從而得到一個更加科學合理的評價結果[7]。在評價指標上，除參考相關研究選取容重和抗拉強度外[8]，本文依據爆破中礦巖的破壞主要呈現為脆性破壞這一現象，引入脆性指標[9]，簡易、直觀地描述礦巖爆破難易程度。

1 礦巖脆性指標的引入及試驗

1.1 脆性指標的引入

脆性表示沒有明顯變形就發生破裂。由于目前對于脆性還沒有明確的定義，所以對脆性的度量、實驗方法還沒有統一的標準。在這方面，許多人做了有益的探索，提出了不同的思路，如：用應變表示的脆性指標，認為脆性指數為可恢復應變與總應變的比值；用能量表示的脆性指標，認為脆性指數為可恢復能ωre與總能量ω的比值；用壓痕硬度表示的脆性指標；用軟化模量定義的脆性指標等[10]。

從變形破壞角度來看，脆性巖石破壞時不產生或很少產生塑性變形，易于在低能耗的情況下即被充分爆破；從能量觀點來看，脆性礦石內部儲存能量較大，在爆破作用下這些能量急劇釋放出來作為破碎礦石的補充能量，有效增加了用于破碎礦石的有效能量。從生產反饋來看，脆性也是爆破作業人員一種感性描述，即脆的巖石容易爆。因此，我們把脆性系數作為描述可爆性的一種新指標加以利用。

1.2 脆性指標試驗研究

由于缺乏統一的定義和規定，現階段脆性有著較多的測定方法，在應用上也比較開放，處于探索階段。因此，研究重點是能否用一種方便簡單的方法快速測定脆性，以便將脆性這一特征引入到更廣泛的實際應用。基于對礦巖特性的考慮及礦山現場收集到的信息，從能量原則出發，采用基于沖擊破碎實驗的礦巖脆性測定方法——落錘法[11]來進行試驗研究。落錘法測定礦巖的脆性有著取樣簡便、測定快捷的優點，但這種方法擺脫不了礦巖的尺寸效應對脆性的影響。

試驗將各巖樣制成40～50 mm的標準小樣，稱1 000 g一份，每種礦巖各三份。將沖擊筒放置在砼或水泥地板上，放入試件一份，將18 kg重錘提高到900 mm高度，使其自由落下沖擊試樣，每份沖擊10次。把每種礦巖沖擊破碎后的試樣依次倒入孔徑10 mm分樣篩中篩分，分別測得篩分后樣品質量，求平均值，試驗數據整理見表1。從試驗數據上來看，四種礦巖的篩上百分率有著明顯的差別。磁鐵富礦的篩上比例最低，即脆性較好，篩上比例最高的是角閃斜長片麻巖，脆性最差。

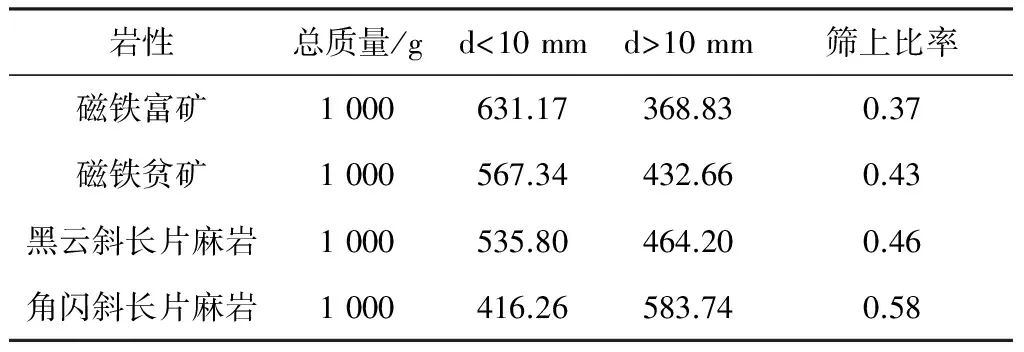
表1 沖擊破碎試驗粒度分析

2 基于物元理論的分級計算

本文引入物元理論進行優化改進，具體的理論與過程分析見參考文獻[7]，具體的計算方法如下所述。

2.1 評價因素選擇與分級標準

根據現場生產反饋和爆破破巖理論，選擇巖石的容重、抗拉強度和巖石脆性系數三個指標進行評價，理由如下所述。

1) 巖石的容重是巖石的最基本的性質之一。根據爆破理論，巖石爆破過程中，巖塊破碎后的移動和拋擲需要爆破能量做功，而做功所需要的能量大小與巖石的容重有直接關系，容重大做功就多，耗費能量也多，巖石就越難破碎。

2) 巖石的抗拉強度是反映巖石爆破重要的力學參數。根據爆破理論，巖石在發生爆破破壞時，由于壓應力產生的破壞僅僅是發生在爆心周圍比較小的范圍內，而其余范圍的破壞諸如藥包周圍的徑向裂隙主要是由于拉伸作用產生的。本文認為巖石力學參數中抗拉強度更具有關聯性，更能表征巖石可爆性。

3) 巖石的脆性系數是直觀反映巖石可爆性的一個新型指標。本文中，采用破碎實驗測定篩上比率的方法測定脆性系數，篩上比率越小，脆性系數越小，巖石越好爆，這也是一種成本型指標。

結合以上三個評價指標和表2各待評巖體參數，參考文獻[1]～[4]中巖體可爆性分級相關研究，將巖體的可爆性分為5個等級：Ⅰ易爆；Ⅱ較易爆；Ⅲ中等可爆；Ⅳ較難爆；Ⅴ難爆。得到的標準評價表及各等級的隸屬范圍見表3。

2.2 物元與待評物元的確定

按照事物、事物的特征以及特征值來構建可爆性分級的物元模型，即R=(N，c，ν)=(事物的名稱，事物的特征，事物的特征值)。根據表2，建立4種巖體的待評物元R1、R2、R3、R4。根據表3，以各評價指標對應的各等級的隸屬范圍作為經典域，建立經典域的物元R0。

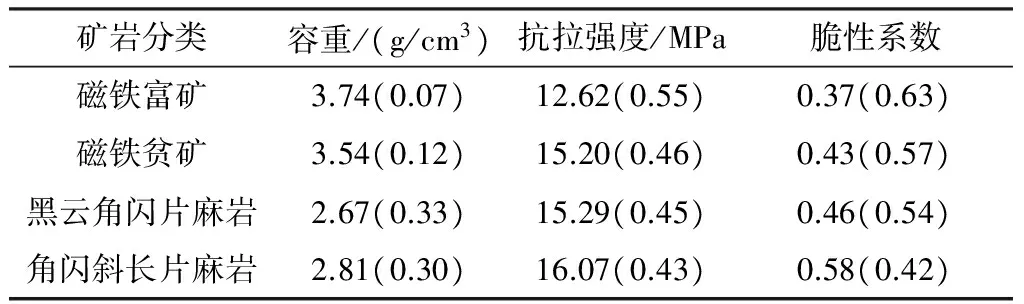
表2 礦巖參數

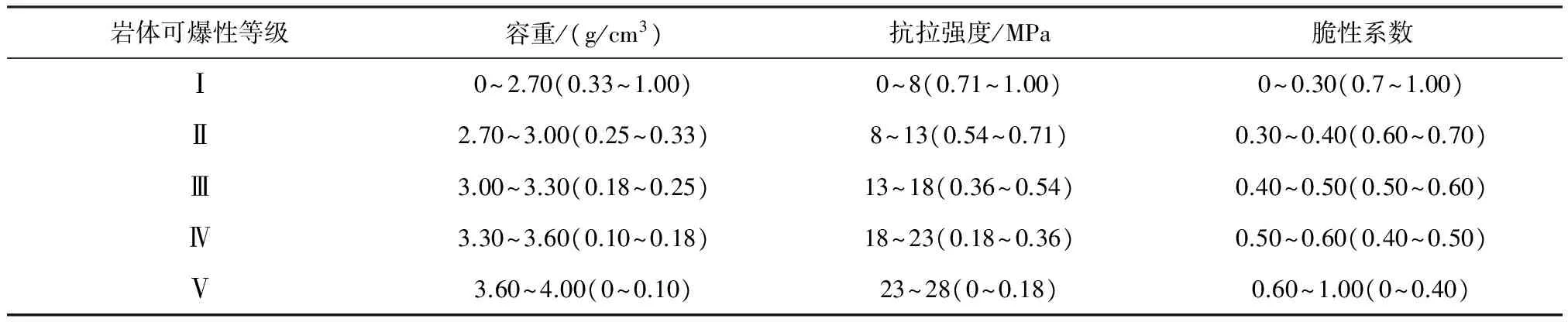
表3 礦巖可爆性分級

2.3 待評巖體與各可爆性等級的關聯度

對于第i類巖體的第k個可爆性評價指標關于可爆性分級標準的第j類分級關聯度由式(1)表示。

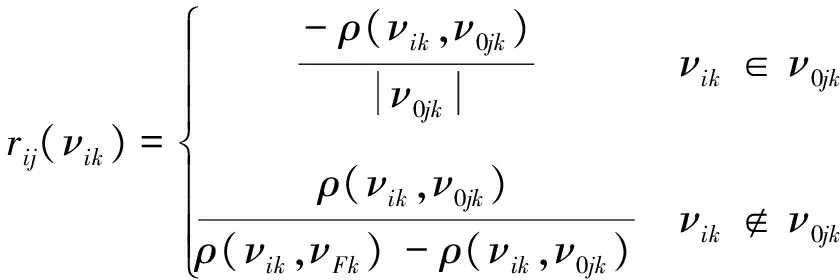
(1)

式中，ρ(vik，v0jk) 與ρ(vik，vFk) 分別為點vik與v0jk、vFk所對應的有限實區間之間的距，是可拓理論中的概念。

通過上述計算，得出待評巖體各特征值對各可爆性等級的關聯度，見表4。

2.4 評價指標的綜合賦權

對于評價可爆性等級各指標的權重，分別用層次分析法和簡單關聯函數進行主、客觀權重的確定。

首先，運用層次分析法確定主觀權重[12]。通過建立遞階層次結構模型，如表5所示，各層次中兩兩比較關系，并構造判斷矩陣；再通過Matlab進行計算并歸一化，即可得到各評價指標的主觀權重，即相對于容重、抗拉強度和脆性系數三個評價指標的權重為ωk=(0.163，0.297，0.540)。

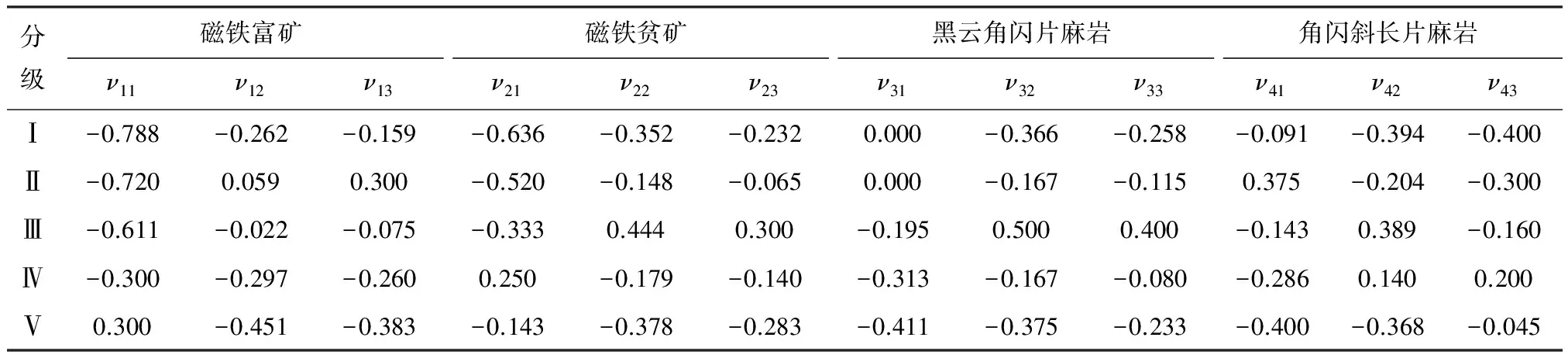
表4 待評巖體的各特征值與可爆性等級的關聯度

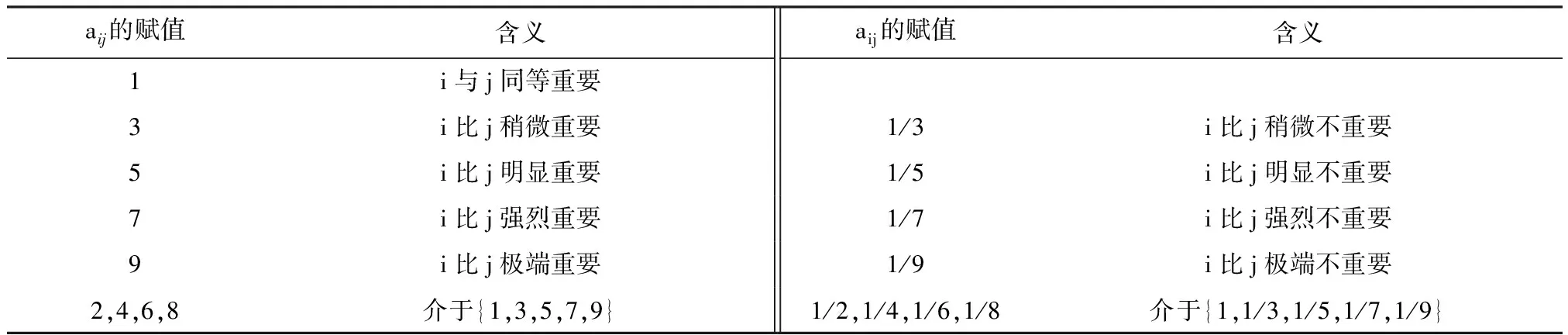
表5 相對重要性比例標度

然后，運用簡單關聯函數計算可爆性評價指標的客觀權重，見式(2)。

(2)

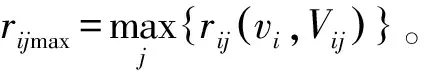
如果特征指標的數據落入的等級類別越大，對考察對象的影響越大時，該指標應賦予越大的權重，γi按式(3)取值。否則，如果特征指標的數據落入的類別越大，對考察對象的影響越小，該指標應賦予的權重越小，即按式(4)取值。

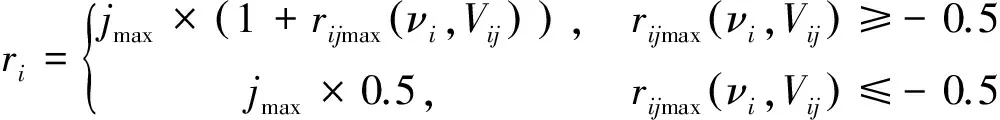
(3)

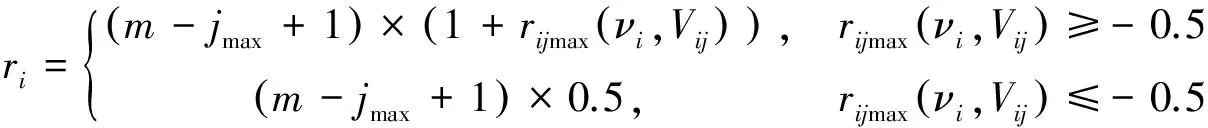
(4)

綜上，可得各特征指標c的客觀權重,見式(5)。

(5)

(6)

2.5 可爆性等級確定

最后，通過計算待評巖體關于各級別的關聯度來評定巖體所屬的可爆性等級。巖體Ni關于級別j的綜合關聯度計算見式(7)。

(7)

其中具有最大關聯度所對應的級別即為巖體Ni的可爆性等級。經計算，得出四種待評巖體可爆性等級的綜合關聯度值，見表7，關聯度與等級對應關系如圖1所示。

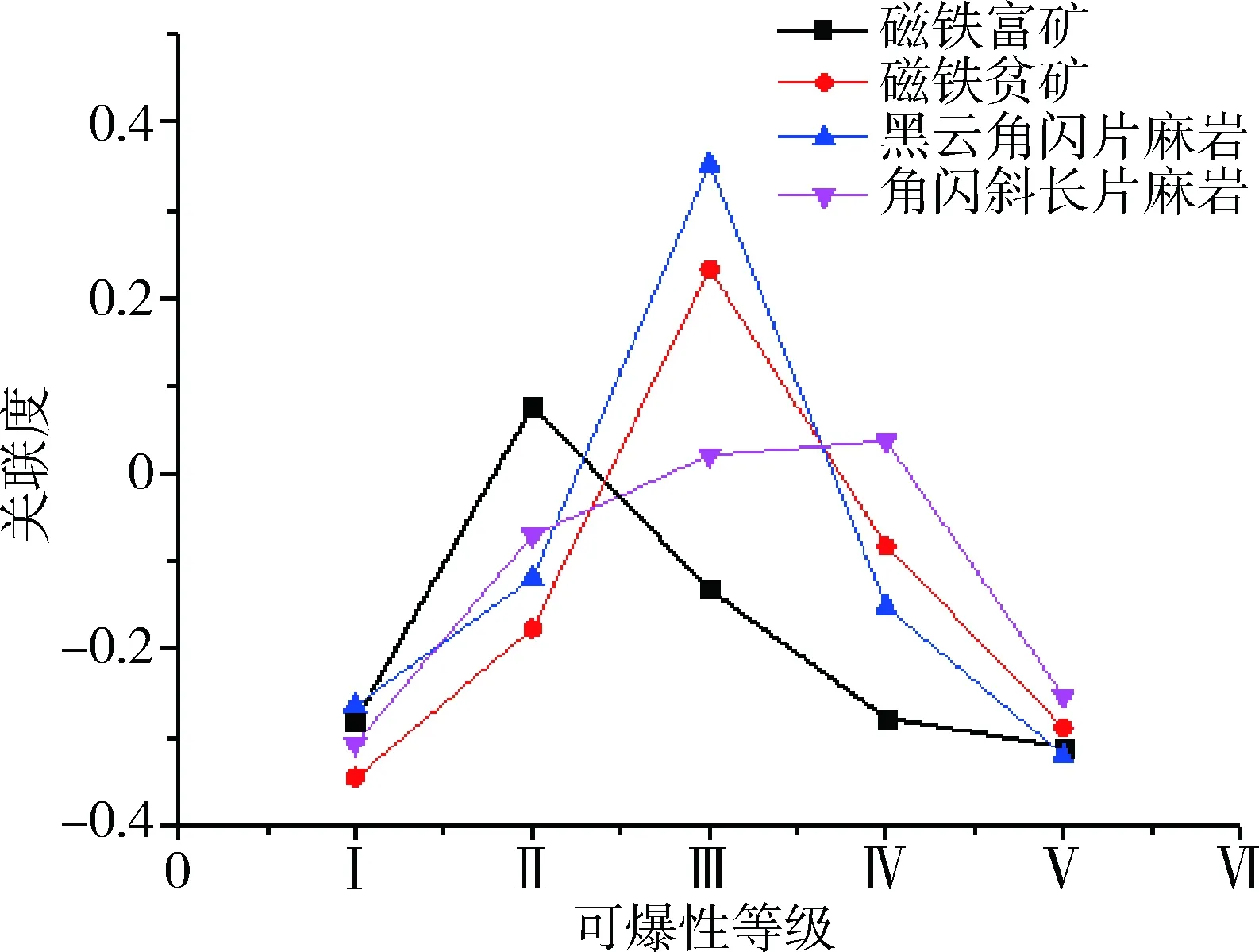
圖1 各待評巖體可爆性等級的綜合關聯度關系

權重磁鐵富礦磁鐵貧礦黑云角閃片麻巖角閃斜長片麻巖ν11ν12ν13ν21ν22ν23ν31ν32ν33ν41ν42ν43主觀0．1630．2970．5400．1630．2970．5400．1630．2970．5400．1630．2970．540客觀0．1280．3590．5130．2230．4210．3560．1420．5370．3210．4640．3510．185綜合0．1390．3390．5220．1830．3380．4790．1520．4220．4260．2950．3210．384

表7 待評巖體關于各等級的綜合關聯度

由圖1可知，該鐵礦磁鐵富礦可爆性等級為第Ⅱ級，較易爆；而磁鐵貧礦與黑云斜長片麻巖可爆性等級為第Ⅲ級，中等可爆；角閃斜長片麻巖可爆性等級為第Ⅳ級，較難爆。

3 基于可爆性分級的驗證試驗及爆破參數優化

3.1 爆破漏斗驗證試驗

本文進行爆破漏斗試驗，一方面可以與實際生產中爆破單耗指標進行比對，另一方面，與本文中可爆性分級方案相互印證，具有重要的實際和理論意義。該試驗選取2號巖石乳化炸藥，炮孔深度1 m，孔間距大于2 m，每孔裝藥量0.45 kg，連續裝藥，炮泥填塞。起爆時，為避免各炮孔之間的相互影響，一次起爆限制在兩個炮孔。

試驗結束后，用爆破漏斗試驗用藥量除以每種巖石的炸藥單耗就可以得到標準測試條件下每種巖石的爆破漏斗體積，試驗結果見表8。雖然這是一個間接獲得的近似值，但因為炸藥單耗來自于生產實際統計，因此具有更高的可靠性和代表性。

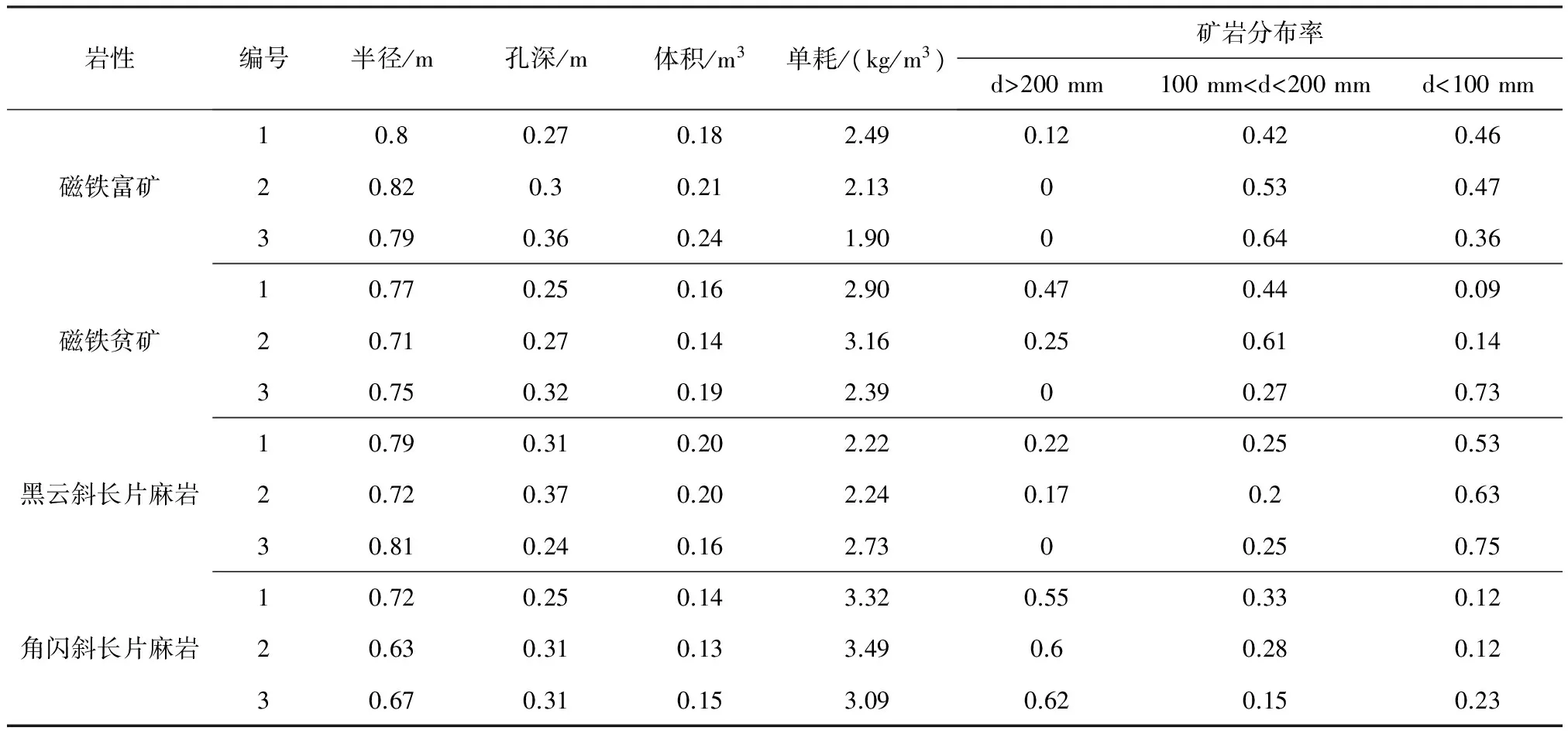
表8 礦巖爆破漏斗試驗結果

從試驗數據上來看，不同巖性中爆破漏斗的體積存在比較明顯的差別，且從爆破漏斗試驗的炸藥單耗和塊度分布來看，磁鐵富礦較好爆，難爆的是角閃斜長片麻巖，這與分級結果一致。

3.2 爆破參數優化

通過對原爆破參數進行分析并結合分級情況進行優化。以磁鐵富礦為例，指出其存在中深孔爆破的排距過小、邊孔角過低等問題。結合相關設計原則和公式進行參數優化：將孔底距由原來的1.5～1.8 m調整為1.7～2.2 m，排間距由1.1～1.3 m調整為排距1.5 m，崩礦步距3.0 m。邊孔角由30°調整為50°，原孔底起爆改為孔口裝藥，采用交錯結構起爆。

優化后，炸藥單耗得到了明顯控制。早期一次炸藥單耗為0.65～0.75 kg/t，最高時甚至達到0.85 kg/t，優化后穩定在了0.48～0.55 kg/t，爆破質量也較好，有效降低了大塊的出現，減少了二次爆破工作量，降低了爆破成本，也提高了后續裝載和運輸環節的效率，提高了采礦強度。

4 結 論

1)通過對現場爆破情況進行分析，首次提出利用脆性反映礦巖受爆破沖擊后的破壞性征。基于能量原則，采用落錘試驗測定待評礦巖破碎后的篩上比例來表征脆性系數，試驗結果表明脆性系數越大，篩上比例越高，礦巖越難以進行破碎。

2)以脆性系數、容重和抗拉強度3個因素作為判別指標，確定待評巖體可爆性等級的判斷標準，建立了可爆性的可判別模型，并運用層次分析法和簡單關聯函數法確定主觀靜態權重和客觀動態權重，得出了磁鐵富礦較易爆，磁鐵貧礦和黑云斜長片麻巖中等可爆，角閃片麻巖較難爆的結果。爆破漏斗試驗結果表明可爆性分級與實際情況相符合。

3)在礦巖可爆性分級基礎上，對爆破參數做出優化，改進爆破方案后，礦山爆破效果有了明顯的改善，礦山生產緊張的局面得到緩解，且炸藥單耗降低25%以上，大大節約了爆破成本。

脆性能夠有效且直觀地表明礦巖爆破性征，但目前基于脆性指標對礦巖可爆性影響的研究甚少，其理論研究和測定量化方法尚有不足，值得進行更進一步的探索。

[1] 鄭偉強，關賢歡，黃鐵平，等.灰色關聯分析在巖體可爆性分級中的應用[J].南方金屬，2009(3)：22-25.

[2] 馮夏庭.巖石可爆性神經網絡研究[J].爆炸與沖擊，1994,14(4)：298-306.

[3] 蔡煜東.巖體可爆性等級判別的遺傳程序設計方法[J].爆炸與沖擊，1995，15(4)：329-334.

[4] 璩世杰，毛市龍，呂文生，等.一種基于加權聚類分析的巖體可爆性分級方法[J].北京科技大學學報，2006，28(4)：324-329.

[5] 汪偉，羅周全，熊立新，等.基于改進物元可拓模型的采空區穩定性評價[J].安全與環境學報，2015,15(1)：21-25.

[6] 陳加良.基于博弈論的組合賦權評價方法研究[J].福建電腦，2003(9)：15-16.

[7] 尚俊龍，胡建華，莫榮世，等.可爆性分級的博弈論物元可拓預測模型及其應用[J].采礦與安全工程學報，2013，30(1)：86-92.

[8] 駱清.巖體可爆性分級現狀及趨勢分析[C]∥中國礦業科技文匯-2013.2013.

[9] 劉恩龍，沈珠江.巖土材料的脆性研究[J].巖石力學與工程學報，2005,24(19)：51-55.

[10] Andreev G E.Brittle failure of rock materials[M].Netherlands Rotterdam，1995.

[11] 林伯泉.用落錘法測定煤體堅固性系數f值的有關參數分析[J].煤炭工程師，1988(6)：5-8.

[12] 何逢標.綜合評價方法MATLAB實現[M].北京：中國社會科學出版社，2010.