基于改進直線特征提取算法的室內移動機器人地圖構建

,,,

(西南交通大學 信息科學與技術學院,成都 611756)

0 概述

自主移動機器人在未知環境中移動,需要根據位置估計和地圖進行自身定位,同時在自身定位的基礎上建造增量式地圖,實現機器人自主定位和導航。這一過程被稱為即時定位與地圖構建(Simultaneous Localization And Mapping,SLAM)。在室內通常采用特征地圖,因其需要更少的內存,能夠更高效全面地提供關于環境的信息。被提取的特征通常是幾何特征,如角和線段,在室內這些特征是很豐富的,可以對障礙物進行表示,并用于建圖和定位。因此,特征地圖被廣泛地研究并用在SLAM中。

從激光雷達掃描室內環境所得數據中提取直線特征的算法主要有分裂合并法[1-2]、增量法[3]、直線回歸法[4]、霍夫變換(HT)[5-8]、隨機抽樣一致性算法(RANSAC)[9-10]、期望最大化算法(EM)等[11-12]。激光雷達對環境的掃描數據具有極角的排列順序,而RANSAC、HT和EM等算法由于自身的算法特性,不會利用掃描數據點的排列順序,試圖虛假地跨順序擬合直線,造成擬合所得直線的假陽性及算法的時間復雜度增高。分裂合并法、直線回歸法和增量法則采用線性回歸方法從掃描數據中擬合直線,但是當掃描數據被大量噪聲干擾時,噪聲點參與直線擬合,造成擬合所得直線的精確性下降。因此,從受到噪聲干擾的大規模離散數據點中剔除噪聲點,精準地提取直線特征,構建精確地圖,實現移動機器人在不同時刻不同位置對同一目標的觀測值相對一致顯得十分重要。文獻[13]討論了在SLAM過程中建圖噪聲去除問題的解決方案。文獻[14]采用無向圖,使用能量函數最小化的方法從2D激光掃描數據中提取直線特征,對噪聲的抑制具有較好的效果。文獻[15]使用在運動連續性和空間連續性上的物理約束來確定噪聲點,但在構建確定性地圖時,計算復雜度較高。文獻[16]運用圖像處理方法,把原始激光掃描數據轉換為二值圖像,每一個掃描點對應一個像素點,對圖像進行腐蝕運算,該算法在移除噪聲點的過程中會把真實點移除,雖采用膨脹算法進行補救,但仍會丟失一些真實點,同時存在轉換誤差,且實時性差。文獻[17]提出一種自適應的圖像線段檢測器,該方法不需要參數調整,可以獲得較精確的提取結果,但是其提取直線特征速度較慢,達不到機器人實時精準建圖的要求。

文獻[18]提出相似三角形法則(STCSM)對每條真實直線上的噪聲點服從的隨機特性進行量化。然后利用統計方法尋找出真實直線的最優方向,以最大程度剔除噪聲點。該方法結合分裂算法,能快速檢測線段,滿足機器人實時建圖。但在確定真實直線最優方向的過程中會誤剔除數據點,導致數據點信息利用率不高造成直線提取精度不穩定。本文針對上述問題提出改進型相似三角形去噪算法。通過雷達在不同位置對障礙物環境進行掃描,從獲得的掃描數據中提取直線特征。

1 直線特征提取算法

本文直線特征提取算法分為下面的5個步驟:數據預處理,數據分裂[2],改進相似三角形法則去噪,去噪數據再次分裂,最小二乘直線擬合。激光掃描數據點在激光雷達自身的掃描坐標系表示為為極坐標形式P(α,r)。數據預處理時計算第i個點Pi(i=2,3,…,m-1,其中m為激光數據點的總數)與前后相鄰點Pi-1和Pi+1之間的極徑差值分別為k1和k2。若k1和k2符號同號,并且其絕對值均大于閾值dc,則該點作為噪聲點。然后對預處理后的數據進行分裂,得到分裂點集,對每2個相鄰分裂點之間的所有數據點采用改進相似三角形算法去噪。最后對去噪后的數據點重新進行分裂,并進行最小二乘直線擬合,計算直線參數和擬合誤差。

算法直線特征提取算法

輸入原始激光掃描數據,參數dc、dth、dr、bin、ε、ds

輸出所有線段所在直線的參數列表S

1.數據預處理(dc),輸出數據集Data1

2.數據分裂(dth,Data1),輸出分裂點集合M1

3.foreach M1中每兩相鄰分裂點間的數據點 do

4.改進型相似三角形法則去噪(dr,bin,ε)

5.end

6.輸出數據集Data2

7.數據分裂(dth,Data2),輸出分裂點集合M2

8.foreach M2中每兩相鄰分裂點間的數據點do

9.最小二乘直線擬合(ds)

10.end

11.輸出直線參數列表S

1.1 相似三角形法則去噪

由于在相鄰2個分裂點之間的大部分離散點在誤差允許范圍內屬于目標直線,同時離散點相對于真實目標直線左右波動的距離關系可以認為服從零均值的正態分布,因此假設目標直線已知,構建一條與目標直線相交于點O的參考直線lr,同時2條直線之間的夾角為γ。令某2個相鄰分裂點間的m個離散點構成集合{Pi|i=1, 2,…,m},則離散點Pi與Oi、O構成RtΔPiOiO,其中Oi是Pi到直線lr的垂線的垂足。此時所有離散點到目標直線距離關系可被間接量化為某一分布X～M(μ,σ2),且該分布的眾數為γ,其中X={Xi|Xi=∠PiOOi}。理論上所有屬于目標直線的離散點Pi,其對應的Xi會集中分布于X的眾數γ。相似三角形去噪算法的執行步驟如下[18]:

步驟1在點集U={Pi|i=1,2,…,m;i≠m}中,以離散點Pi作為基準參考點,以點Pi和點Pm兩點擬合直線li′,并以離散點Pi為旋轉中心,把直線li′順時針旋轉角度θ(即γ=θ,5°<θ<10°)得到參考直線li,如圖1所示。

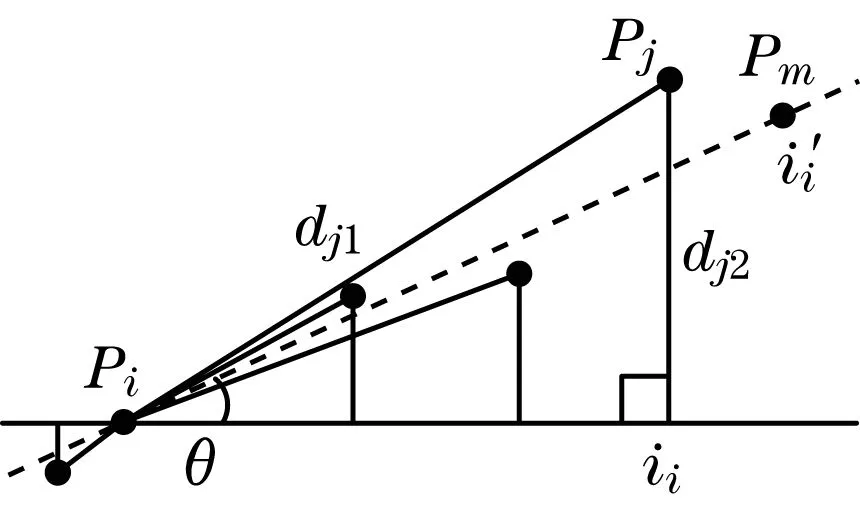
圖1 相似三角形法則去噪示意圖

步驟2對集合W={Pj|j=1,2,…,m-1;j≠i}中的點進行遍歷。計算每一個點Pj與參考點Pi的距離dj1以及點Pj與參考直線li的距離dj2,求比值cij=dj2/dj1。當遍歷完W中所有點后,得到數據集Q={cij|j=1,2,…,m-1;j≠i}。

步驟3求數據集Q的眾數。在數據集Q的最大值和最小值之間進行S等分,得到S個區間間隔。統計在S個區間中的最大頻數ni-max以及該頻數對應的區間平均值ci-max。如果ni-max>nmax,那么令nmax=ni-max、cmax=ci-max、num=i,進入步驟4;否則,直接進入步驟4。其中,眾數nmax表示對集合U中每一個點Pi執行算法步驟1～步驟4后經比較保存的最大區間頻數,cmax表示nmax對應區間的平均正弦比例值,num表示nmax對應的基準參考點Pi在原始數據點中的排列序號。

步驟4當點集U中所有點都作為參考點,并執行算法步驟1～步驟3后,進入步驟5;否則把下一個離散點Pi+1代替Pi作為基準參考點并跳轉至步驟1。

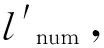
步驟6計算Pk(k=1,2,…,m)到直線l′的距離θi,若dk大于閾值dr,則把點Pk記為噪聲點。算法結束。

相似三角形去噪算法的時間復雜度為O(m2),算法可以歸納為尋求函數J最優的過程:

(1)

其中:

(2)

其中,δ為ci-max對應區間的長度。

相鄰分裂點間的所有離散點到目標直線的距離關系可被間接地量化為某一分布X～M(μ,σ2),當進行正弦函數映射后,Y=sin(X),Y與X的分布不再一致,在步驟3中求出的ci-max所對應的角度arcsin(ci-max)與X的眾數值不嚴格相等。當X較小時,Y=sin(X)≈X,此時Y的分布可以近似為X的分布,角度arcsin(ci-max)則可作為X的眾數值。由圖1可知,集合{Pj|j=1,2, …,m-1;j≠i}中的任意點Pj,其對應的arcsin(d2/d1)在θ附近波動,即arcsin(d2/d1)≈θ,而arcsin(d2/d1)正是隨機變量X的一個樣本點。所以,取5°<θ<10°,就能使Y的分布與X的分布近似一致。

參數S的取值將影響γ的精確性,S由式(3)給出:

S=[max(cij)-min(cij)]/bin

(3)

其中,cij∈Q,bin是各區間間隔值,其實際取值視需要的精度而定,通常較小。

1.2 改進相似三角形去噪法則

當集合U={Pi|i=1,2,…,m;i≠m}中的點Pi作為參考點時構建參考直線,并且相似三角形去噪算法步驟3被執行完成后,可以得到數據Q={cij|j=1,2,…,m-1;j≠i}。假設cij的分布直方圖對應的輪廓線如圖2所示。

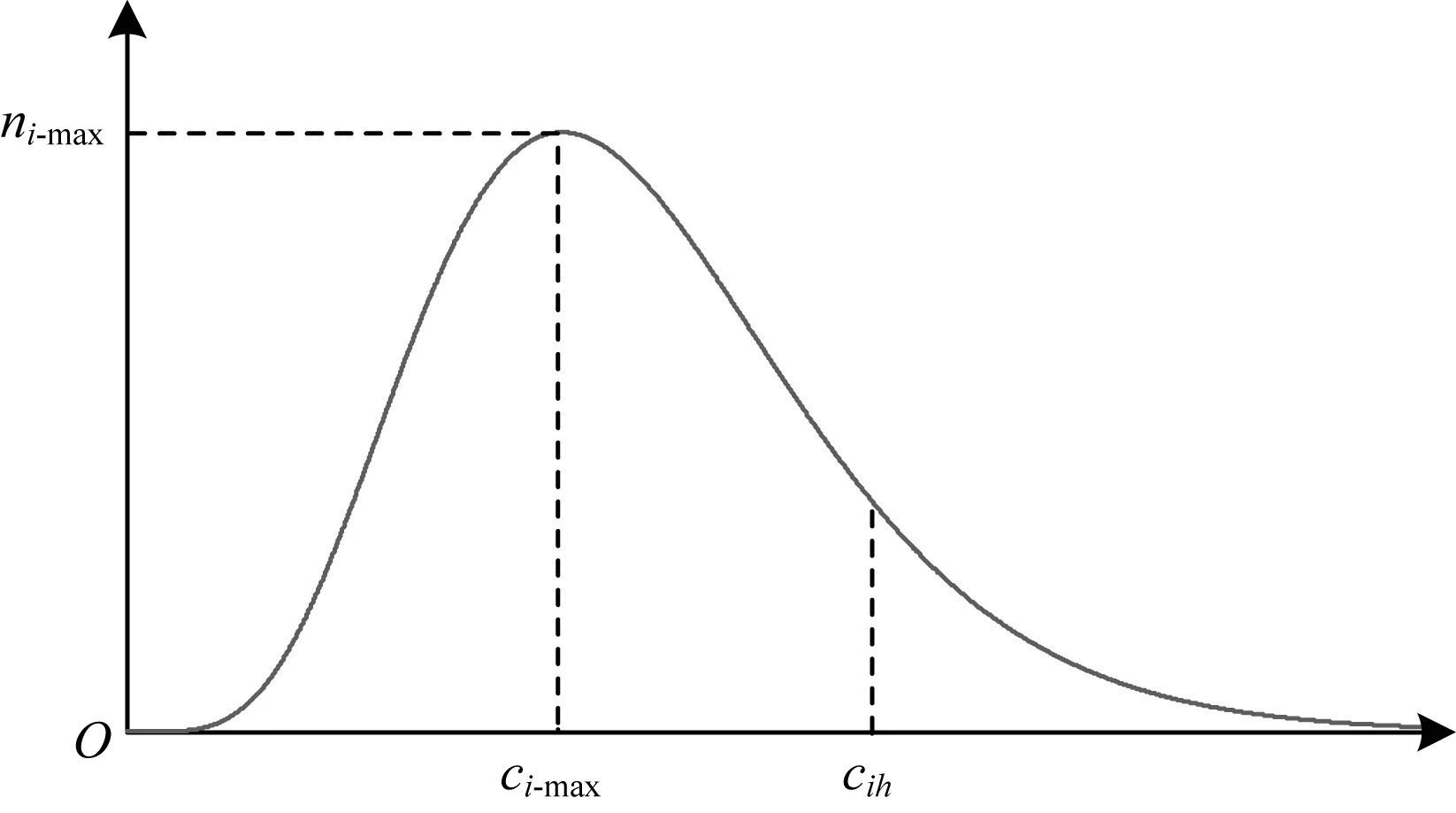
圖2 cij分布直方圖輪廓線

在圖2中,ci-max表示當以Pi作為參考點時,數據集Q的眾數,ni-max表示ci-max對應的頻數,cih對應圖3中的Ph點。

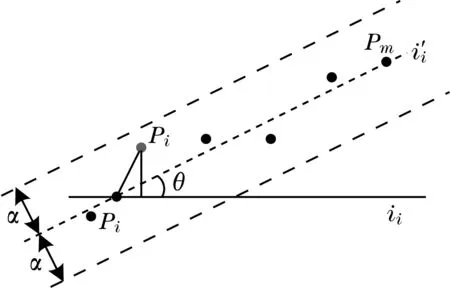
圖3 參考點Pi鄰域內的離散點分布

假設圖3中直線li′是目標直線,左右兩邊的虛線與li′的距離均為dr。由相似三角形去噪算法步驟6可知,離散點到目標直線的距離是否大于閾值dr決定該點是否是噪聲點。因此,圖3中2條虛線間區域內的點都不該視為噪聲點,在此區域內離散點的位置信息需被利用起來確定最終的真實目標直線。圖3中點Ph與參考點Pi的距離dh1很小,Ph對應正弦值cih?sinθ。據相似三角形去噪法則原理,cih不會被包含在用于確定目標直線的離散數據點集合;但Ph處于閾值區域內,應為確定目標直線做出貢獻。由上述分析可知,在參考點Pi的某一空間鄰域內會出現較多屬于閾值區域內的Ph點,忽略這些點的信息將導致求得的目標直線參數不準確。本文針對這一問題提出改進算法,在相似三角形去噪法則的步驟3之后對ni-max進行更新。

算法ni-max更新

輸入基準參考點Pi,及對應的分裂區間點集U、參考直線li、數據集Q、ci-max和ni-max

輸出ni-max的更新值

1. 求φ=arcsin(ci-max)

2. 根據φ、li求出直線lm

3. foreach Pj∈U do

4. if cij?Q

5. 計算Pj到直線lm的距離dj-m

6. if dj-m>dr

7. ni-max++

8. end

9. end

10. end

11. 輸出ni-max

閾值dr的大小隨著原始探測數據的線性一致性增大而減小。當環境中障礙物表面粗糙程度差異較大時,可對U中的點進行二維PCA處理,dr可自適應取值為在次分量方向上數據投影的方差;否則可取dr為定值。

1.3 直線擬合及特征提取

當所有相鄰分裂點構成的線段區間上的離散點經過相似三角形法則去噪后,對去噪后的所有點重新執行分裂算法,得到精確的分裂點集。按照分裂點的順序,對相鄰2個分裂點之間所有非噪聲點的數目進行統計,若點數小于閾值ds,則舍棄該線段區間,否則利用最小二乘法擬合直線。擬合所得直線l表示為:

d=rcos(α-θ)

(4)

其中,d為原點到直線l的垂線長,θ為垂線與極軸的逆時針方向的夾角,(α,r)為直線l上的點P(α,r)。

θ和d由式(5)、式(6)給出:

(5)

(6)

(7)

F=

(8)

(9)

其中,N為參與擬合直線l的離散點個數,F為Jacobian矩陣,C為參與擬合直線l的N個激光測距點參數的協方差矩陣。

2 實驗結果與分析

本文使用RPLIDAR360°激光測距儀對12 m×6 m的實驗環境進行掃描。雷達有效測距半徑為6 m,設置其掃描間隔為0.25°,得到693個掃描點。分裂算法的分裂閾值dth為70 mm,相似三角形去噪過程中的統計區間間隔設為sin 0.5°,距離閾值dr為定值5 mm,再次分裂并擬合直線步驟中的點數閾值ds為5。測量極角的方差忽略不計,測量距離的方差與測量距離的關系如圖4所示。

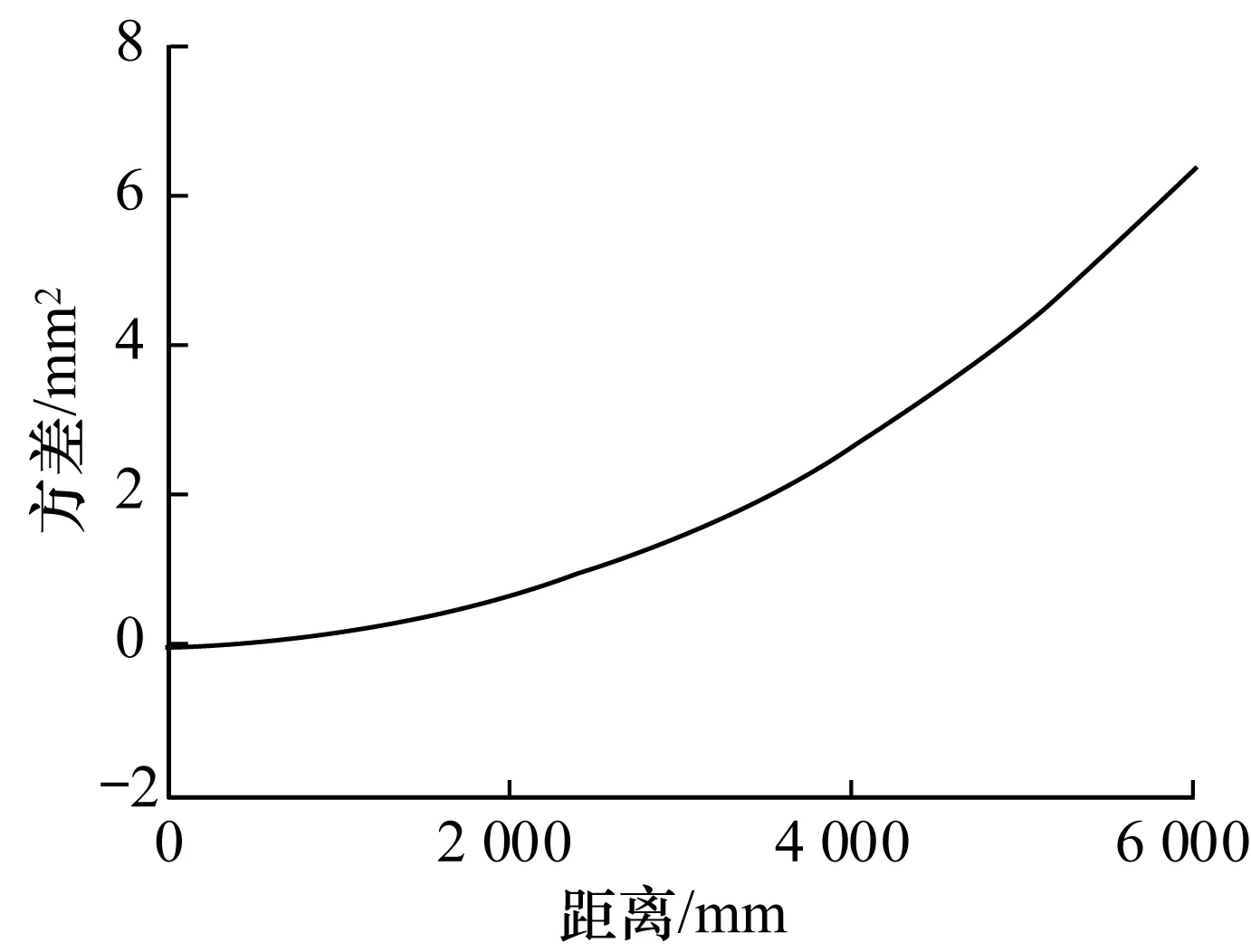
圖4 測量距離方差與測量距離的關系

2.1 算法精度

測試環境如圖5(a)所示,實驗中激光雷達的測量中心所在位置為原點O,沿其測量極坐標系的極軸方向建立x軸,相應建立y軸。采用改進相似三角形去噪算法,最終擬合直線的結果如圖5(b)所示,得到7條直線,與真實障礙物環境中的直線相吻合。由于改進相似三角形去噪法則能最大程度剔除噪聲點及利用有效點確定真實直線所在方向,因此沒有線段合并的過程。各條擬合所得直線的參數如表1所示。表1中皮爾遜系數表示根據如圖5(b)所示的離散點擬合所得各直線的線性程度。點數比例表示去噪后參與擬合各條直線的離散點數在線段區間上的原始數據點數中所占比例。擬合所得各線段的點數比例最低為45.07%,平均比例為52.25%。由相似三角形去噪算法改進原理可知,算法去噪建立在噪聲點服從正態分布的隨機特性基礎上,能避免大量的局部大面積去噪。因此,去噪后的數據點能準確描述真實直線的信息。相關系數最小值為0.999 972,擬合各條直線的離散點線性相關性均趨近1。由此表明本文算法保證在不丟失原始數據絕大部分信息的前提下,利用線性程度較高的數據點擬合得到直線參數。同時,實驗所得直線參數精度也較高,直線li參數di的方差的最高數量級為10-1mm2,參數θi的方差的最高數量級為10-5rad2,針對該激光掃描器的特性而言,算法滿足對環境的精確建模。

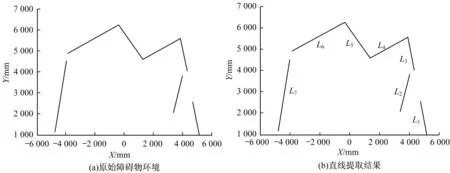
圖5 采用改進相似三角形法則提取的環境直線

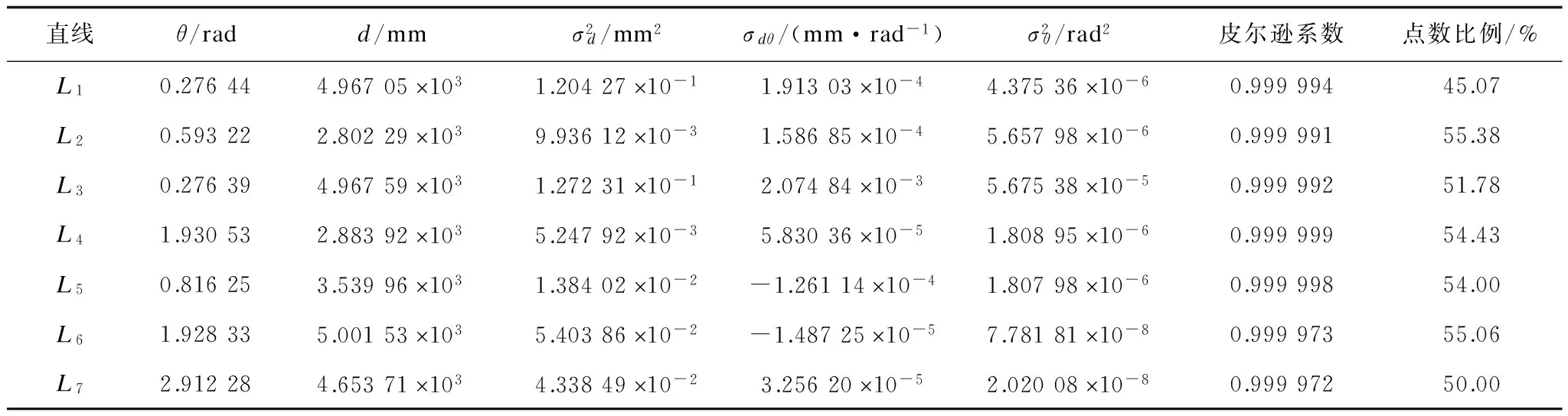
直線θ/radd/mmσ2d/mm2σdθ/(mm·rad-1)σ2θ/rad2皮爾遜系數點數比例/%L10.276444.96705′1031.20427′10-11.91303′10-44.37536′10-60.99999445.07L20.593222.80229′1039.93612′10-31.58685′10-45.65798′10-60.99999155.38L30.276394.96759′1031.27231′10-12.07484′10-35.67538′10-50.99999251.78L41.930532.88392′1035.24792′10-35.83036′10-51.80895′10-60.99999954.43L50.816253.53996′1031.38402′10-2-1.26114′10-41.80798′10-60.99999854.00L61.928335.00153′1035.40386′10-2-1.48725′10-57.78181′10-80.99997355.06L72.912284.65371′1034.33849′10-23.25620′10-52.02008′10-80.99997250.00

2.2 算法準確性

把激光雷達的測量中心分別平移到如圖6(a)所示標號的位置(xj,yj)處對環境進行掃描,j=1,2,…,14。雷達在(x1,y1)處的測量坐標系作為全局不變坐標系。因此,直線li(θi,di),i=1,2…,7,在平移前后的雷達極坐標系中的參數(θi1,di1)、(θij,dij)滿足下式:

Δθi=|θij-θi1|

(10)

(11)

其中,Δθi稱為平移不變性參數,理論上Δθi=0。由于直線li的準確參數(θi,di)無法預知,因此無法對激光雷達平移前后的直線參數進行式(11)的檢驗。但由式(5)、式(6)可知,參數di的準確性依賴于θi,直線極角的準確性在一定程度上能保證極徑的準確性。因此,對平移前后的直線參數進行式(10)的檢驗即可評價算法的準確性。

激光雷達在位置(xi,yi)處掃描環境獲得一幀數據時,分別采用傳統分裂合并法、STCSM算法和本文改進算法進行直線提取。當雷達在所有標號位置處對環境掃描結束,采用每一種算法提取完成直線后,均可得直線極角的集合R={θij|j=1,2,…,14},分別對3種方法所得集合R的元素進行方差分析,結果如圖6(b)～圖6(h)所示。從圖6(b)～圖6(h)可以看出,采用本文改進算法在不同測量位置提取的各條直線參數的方差最小,最大數量級為10-6rad2,即在機器人移動過程中保持的直線平移不變性要優于采用傳統分裂合并法和STCSM算法。隨著雷達平移,障礙物輪廓線L1、L2和L3被激光掃描得到的點逐漸減少,同時激光雷達在位置11～位置14處時,線段L1不在雷達0°～180°的視野內,因此圖6(b)～圖6(d)中所示直線極角參數的方差相較于其余直線參數偏大。圖6(e)～圖6(h)表明,在不同位置提取的線段L4～L7角度參數的波動幅度很小,平移不變性參數Δθi≈0。

西格沃特等[2]的研究結果表明:就正確性而言,增量法表現最好,其假陽性約6%;分裂合并法其次,其假陽性約10%;同時分裂合并法的執行速度是所有算法里最快的,但是該算法的精度卻不是最高的。RANSAC、HT、EM算法較于分裂合并法其提取直線的速度非常慢,假陽性較高,但是它們能夠產生比其他算法更精確的直線,其原因在于它們有能力去除異常點和噪聲大的有效點。綜上分析,本文提出的基于改進相似三角形去噪算法有能力去除異常點或噪聲大的有效點有效提高了提取直線的精度。

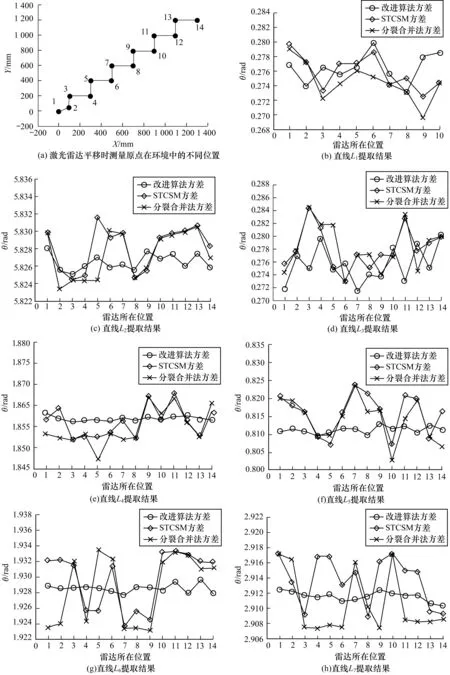
圖6 雷達在不同位置對環境掃描并采用不同方法提取直線結果及對比

3 結束語

在相似三角形去噪法則剔除噪聲點過程中,噪聲點相對于真實直線的空間位置所呈現的分布進行量化存在非線性量化誤差,進而會剔除部分有效點。本文提出的改進相似三角形去噪算法降低了誤剔除有效點的數量。在12 m×6 m的障礙物環境中進行實驗,得到在0°～180°的掃描范圍內693個點。直線參數極徑di的方差數量級在10-1mm2以下,極角θi方差的數量級最高為10-5rad2。激光雷達在不同位置對環境掃描并提取直線的角度參數的方差數量級最大為10-6rad2。實驗結果表明,本文提出的改進算法在直線提取的準確性和精度方面都優于傳統分裂合并法、增量法、直線回歸法、RANSAC、HT和EM算法,對室內機器人精準魯棒地實時地圖構建、路徑規劃、全局定位具有重要意義。

[1] PAVLIDIS T,HOROWITZ S L.Segmentation of Plane Curves[J].IEEE Transactions on Computers,1974,23(8):860-870.

[2] NGUYEN V,MARTINELLI A,TOMATIS N,et al.A Comparison of Line Extraction Algorithms Using 2D Laser Rangefinder for Indoor Mobile Robotics[C]//Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems.Washington D.C.,USA:IEEE Press,2005:1929-1934.

[3] AHMAD H,NAMERIKAWA T.Robot Localization and Mapping Problem with Unknown Noise Charac-teristics[C]//Proceedings of IEEE International Conference on Control Applications.Washington D.C.,USA:IEEE Press,2010:1275-1280.

[4] ARRAS K O,SIEGWART R Y.Feature Extraction and Scene Interpretation for Map-based Navigation and Map Building[C]//Proceedings of MRXI’97.[S.1.]:SPIE Press,1997:42-53.

[5] WANG C F.Fast Line Extraction Algorithm Based on Improved Hough Transformation[J].Advanced Materials Research,2014(926-930):3612-3615.

[6] XU Zezhong,SHIN B,KLETTE R.Accurate and Robust Line Segment Extraction Using Minimum Entropy with Hough Transform[J].IEEE Transactions on Image Processing,2015,24(3):813-822.

[7] 王競雪,朱 慶,張云生,等.疊置分區輔助的相位編組直線提取算法[J].測繪學報,2015,44(7):768-774,790.

[8] 張 帆,高云龍,黃先鋒,等.基于球面投影的單站地面激光點云直線段提取方法[J].測繪學報,2015,44(6):655-662.

[9] CANAZ S,KARSLI F,GUNEROGLU A,et al.Automatic Boundary Extraction of Inland Water Bodies Using LiDAR Data[J].Ocean and Coastal Management,2014,118(1):158-166.

[10] FISCHLER M A,BOLLES R C.Random Sample Consensus:A Paradigm for Model Fitting with Application to Image Analysis and Automated Cartography[J].Communications of the ACM,1981,24(6):381-395.

[11] NGUYEN V,GACHTER S,MARTINLLI A,et al.A Comparison of Line Extraction Algorithms Using 2D Range Data for Indoor Mobile Robotics[J].Autonomous Robots,2007,23(2):97-111.

[12] PFISTER S,ROUMELIOTIS S L,Burdick J W.Weighted Line Fitting Algorithms for Mobile Robot Map Building and Efficient Data Representation[C]//Proceedings of IEEE International Conference on Robotics and Automation.Washington D.C.,USA:IEEE Press,2003:1304-1311.

[13] RAO A,MULLANE J,WIJERUPAGE W S,et al.SLAM with Adaptive Noise Tuning for the Marine Environment[C]//Proceedings of OCEANS’11.Washington D.C.,USA:IEEE Press,2011:1-6.

[14] LI Xinzhao,LIU Yuehu,NIU Zhenning,et al.A Line Segments Extraction Based Undirected Graph from 2D Laser Scans[C]//Proceedings of the 17th IEEE International Workshop on Multimedia Signal Processing.Washington D.C.,USA:IEEE Press,2015:1-6.

[15] YE Cang,BORENSTEIN J.A Novel Filter for Terrain Mapping with Laser Rangefinders[J].IEEE Transactions on Robotics,2004,20(5):913-921.

[16] RAVANKAR A A,HOSHINO Y,RAVANKAR A,et al.Algorithms and a Frame Work for Indoor Robot Mapping in a Noisy Environment Using Clustering in Spatial and Hough Domains[J].International Journal of Advanced Robotic Systems,2015,12(3):57-62.

[17] GROMPONE V G,RAFAEL,JAKUBOWICZ J,et al.LSD:A Fast Line Segment Detector with a False Detection Control [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2008,32(4):722-732.

[18] JIAN Ming,ZHANG Cuifang,YAN Fei,Tet al.A Global Line Extraction Algorithm for Indoor Robot Mapping Based on Noise Eliminating via Similar Triangles Rule[C]//Proceedings of the 35th IEEE China Control Conference.Washington D.C.,USA:IEEE Press,2016:6133-6138.