一種6軸工業機器人的結構設計與運動學建模

（廣東交通職業技術學院 機電工程系，廣州 510800）

0 引言

6軸機器人是工業機器人應用最為廣泛的一種類型[1]。機器人本體結構設計是實現機器人功能的基礎，德國庫卡（KUKA）機器人公司、瑞士ABB公司、日本FANUC公司等所研制的6軸串聯機器人幾乎具備了人類手臂的全部操作功能，但6軸機器人由于大多是垂直旋轉關節，很多時候會出現多軸共線自由度退化的問題，因此此類機器人在諸如焊接的時候，需要從不同的姿態多次焊接，造成焊接時間和質量嚴重下降。

機器人運動學分析是實現機器人運動控制與軌跡規劃的基礎，其中正運動學分析是最基本的問題[2]，而D-H法[3～5]是常用的分析方法，通過仿真可以模擬機器人的運動情況，驗證建立的運動學模型。針對自由度退化，機器人出現奇異點的問題，雖然出現多種解決算法，但是并不能達到完全根除。日本OTC進行了研究，因此推出了特異型5軸6自由度機器人[6,7]。另外通用6軸機器人在焊接的時候任意時間多要通過6軸聯動試驗位姿的插補，因此能耗較大。國外機器人公司從能耗入手提出了很多新穎的機器人，如SCARA機器人等[8～10]。

針對上述的問題，本文提出的新型機器人結構采用5串聯關節+1移動關節的方式組成機器人的本體。具體分配是1、2、3軸為串聯，4軸為平移軸，5、6軸為串聯軸通過第四軸的平移可以解決臂展的問題及避免機器人退化的問題。

1 6軸機器人的結構

本文提出的6軸機器人是由5個串聯軸加一個平移軸組成，機器人1、2、3、5、6軸為旋轉軸，4軸為平移軸，通過4軸的平移可以改變機器人的臂展。這樣機器人的工作區間就是一個球體和圓柱體的結合體，工作范圍加大。利用SolidWorks建立的6軸機器人結構如圖1所示，軸1由基座內的交流伺服電機（軸1電機）和諧波齒輪組成，實現立柱回轉；軸2由肩部的交流伺服電機（軸2電機）和諧波齒輪組成，實現肩關節旋轉；軸3由肩部的交流伺服電機（軸3電機）和諧波齒輪組成，實現肘部轉動；軸4以小臂中心線為軸線，由交流伺服電機（軸4電機）、聯軸器和滾珠絲杠組成，實現手臂的平移運動。為減小轉動慣量，電機安裝在肘關節處，和肘關節電機交錯安裝；軸5由交流伺服電機（軸5電機）、同步帶、諧波齒輪組成，電機安裝在小臂內部末端。實現手腕俯仰P運動，P軸和Y軸（滾珠絲杠）的軸線垂直；軸6由交流伺服電機（軸6電機）、諧波齒輪和法蘭盤組成，電機安裝在腕部。實現手腕翻轉R運動，P軸和R軸的軸線垂直，末端執行器通過法蘭盤安裝在末端。

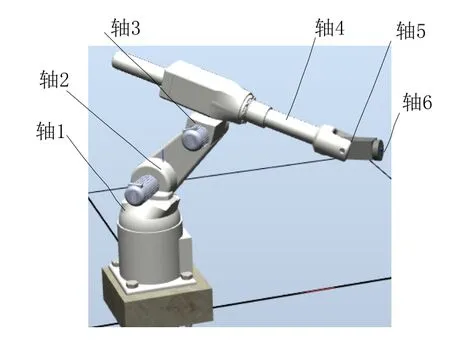
圖1 機器人結構圖

為確保6-DOF機器人運動學算法可靠、高的定位精度，建樣機時應滿足軸1旋轉軸（基座旋轉軸）、軸4平移軸、軸6旋轉軸在同一個平面內；軸2旋轉軸、軸3旋轉軸以及軸5旋轉軸互相平行，而且與前面提到的平面垂直；還需要保證軸4平移軸線、軸5旋轉軸線以及軸6旋轉軸線相交于一點。如果機器人的結構與此差別較大，難以滿足實際的應用。

2 機器人正向運動學建模

機器人正運動學是利用連桿參數表示出末端執行器位姿的過程。下面使用D-H坐標系建立的方法先制定D-H參數表格，如表1所示。

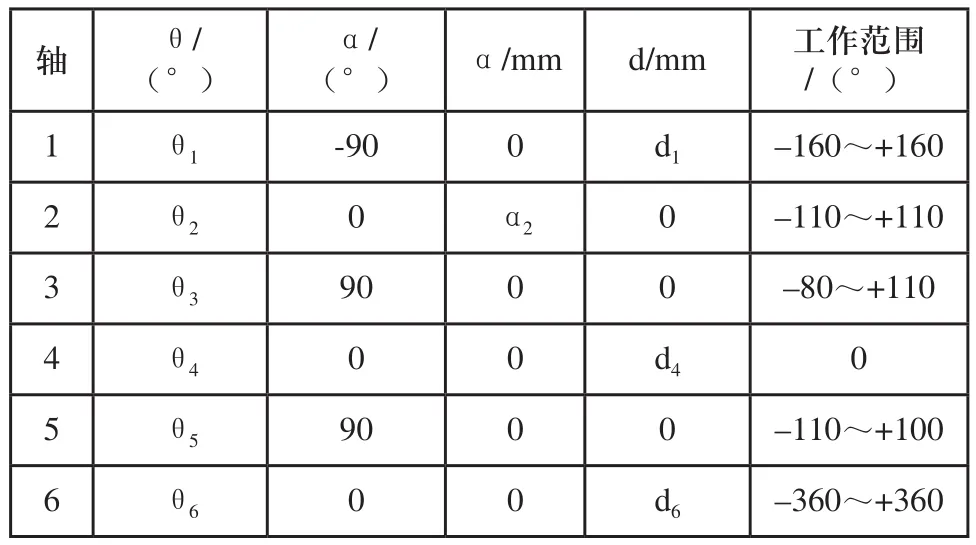
表1 6軸機器人D-H坐標參數

機器人D-H坐標轉換公式：

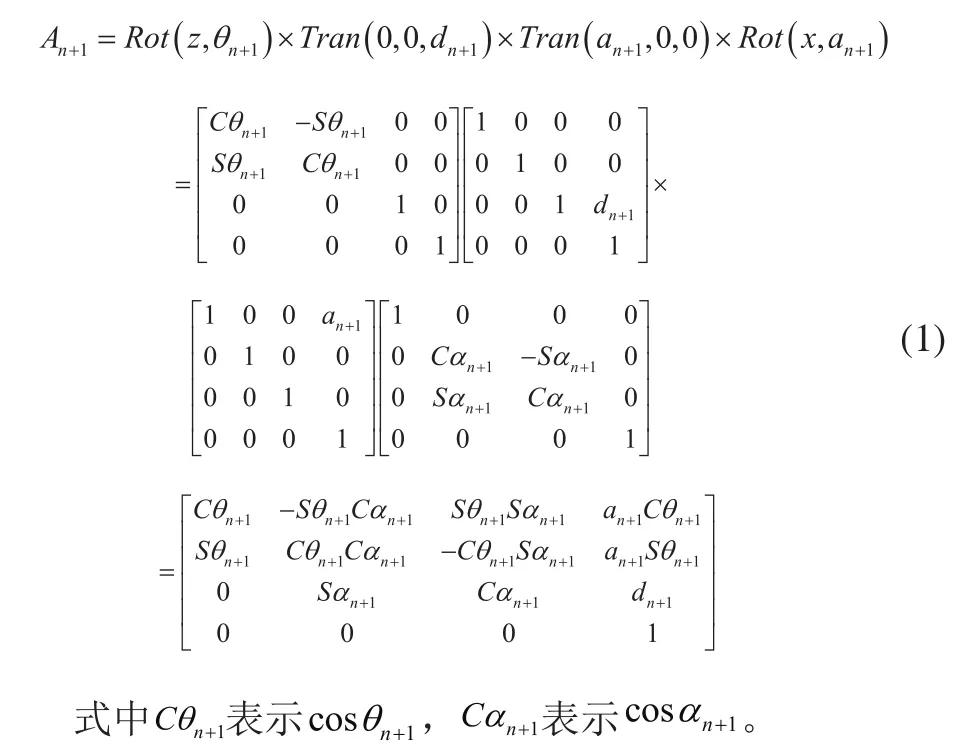
根據式(1)可得出：

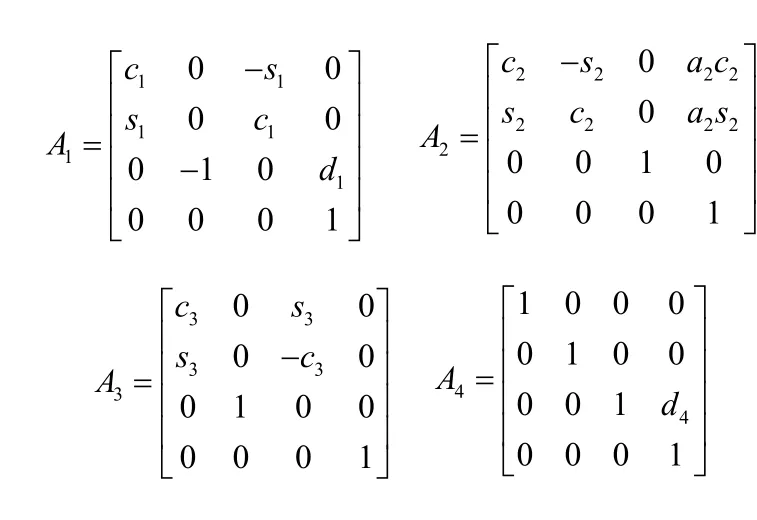
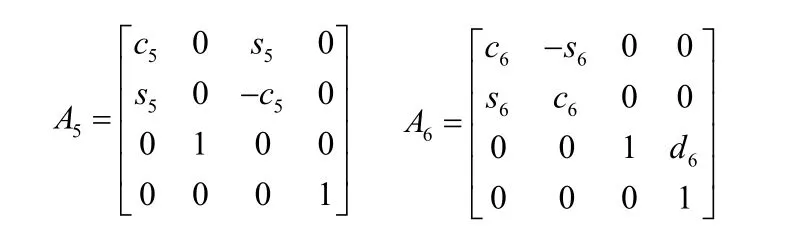
機器人的基座與手之間的總變換則為：

根據式(2)，得出機器人正運動學方程：

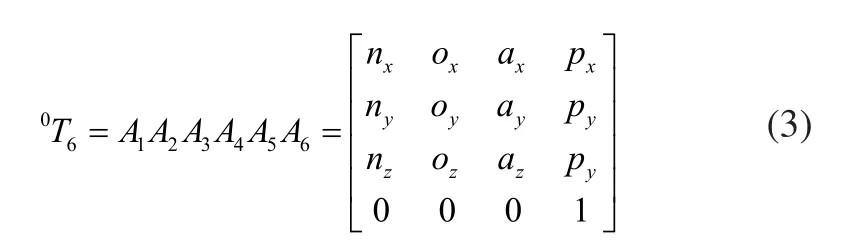
式中：

式(3)即為機器人的正運動學方程，可以通過給定各個關節變量來求得機器人末端執行器的位姿。

3 正向運動學驗證

Robot toolbox是一個專門用來做機器人仿真的軟件包，運行在MATLAB環境下，取機器人的結構參數，a2=0.3，d1=0.2，d6=0.1，根據正運動學方程式(3)，進行驗證，部分軟件代碼如下：

將θ1=-0.2，θ2=-0.1，θ3=0.2，θ5=0.1，θ6=0.6，d4=0.5輸入機器人驅動窗口如圖2中的q1，q2，q3，q4，q5，q6，此時機器人驅動位姿效果如圖3所示。同時在圖2中生成機器人6軸法蘭中心仿真位姿：

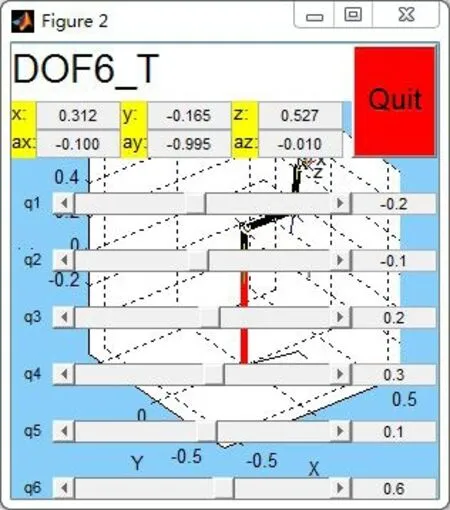
圖2 模擬驅動圖

圖3 機器人位姿圖

為保證論證機器人正運動學模型正確的嚴謹性，并使機器人位姿差異盡可能的大，再取2組機器人角度值如圖4和圖5所示。

圖4 模擬驅動圖

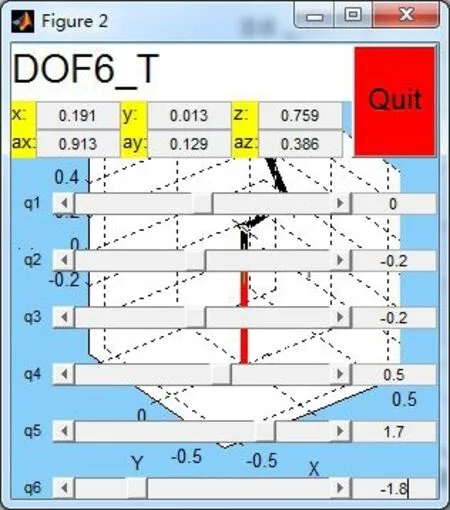
圖5 模擬驅動圖

根據機器人的正運動學方程式(3)，利用Robotics toolbox建立Dof6_fkine函數，并代入三種情況旋轉關節角度和平移關節值，可得出機器人6軸法蘭中心計算位姿。其三種情況理論計算位姿和Robotics計算位姿對比如表2、表3和表4所示。

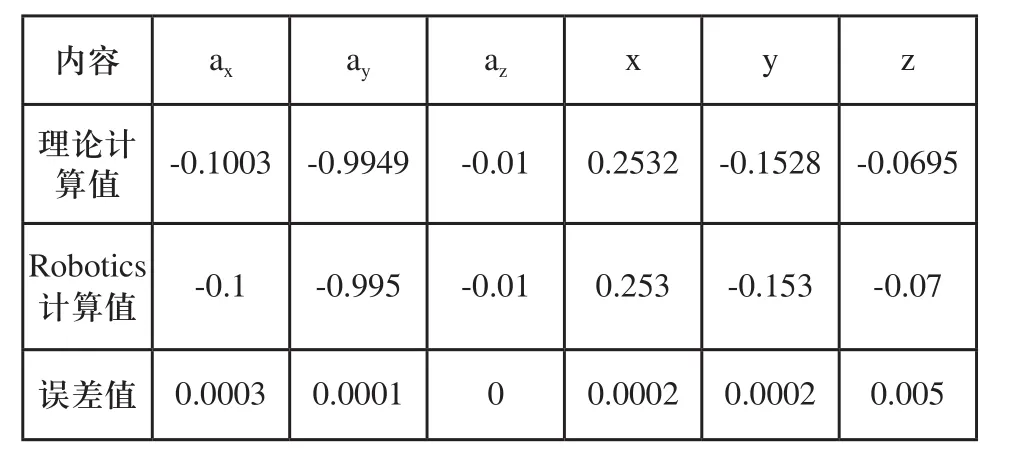
表2 理論計算值與Robotics計算值對比表

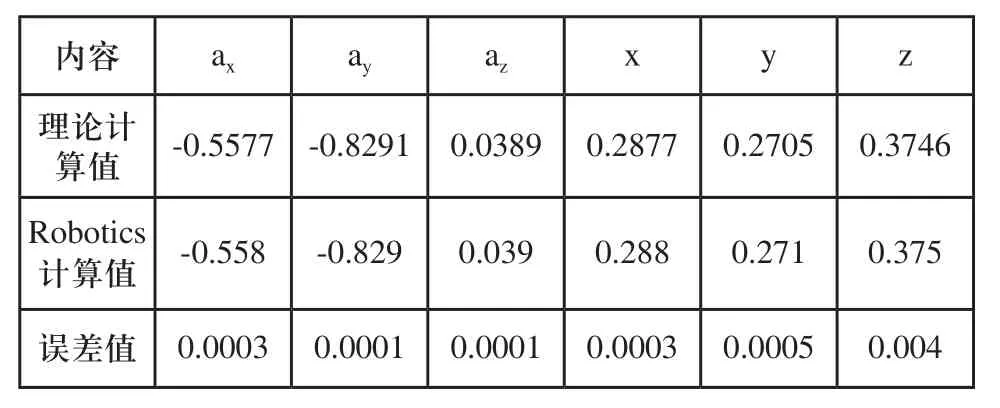
表3 理論計算值與Robotics計算值對比表

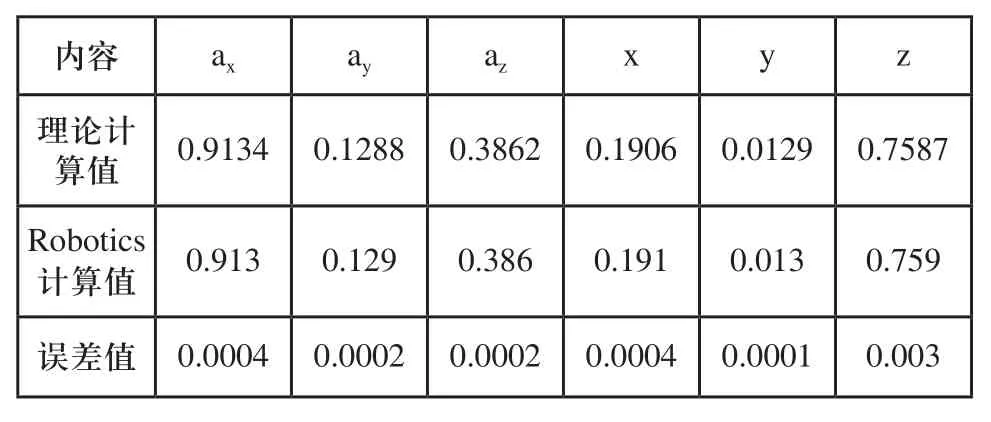
表4 理論計算值與Robotics計算值對比表

數據分析，計算位姿的數據是小數點后四位，實際機器人運行時的精度只能到后三位，因此圖3、4、5窗口仿真位姿顯示的數據是經過四舍五入的。從三組數據計算結果可以看出，機器人的姿態角ax、ay、az，與機器人位置x、y、z的值誤差較小，數量級在小數點后四位，對于機器人來說經過減速機之后角度偏差幾乎可以忽略，因此經過驗證正向運動學模型算法是正確的。

4 MATLAB箱體焊接仿真

運用MATLAB中的Robotics工具箱，仿真焊接一個長寬高為300mm×150mm×600mm的箱體如圖6所示。

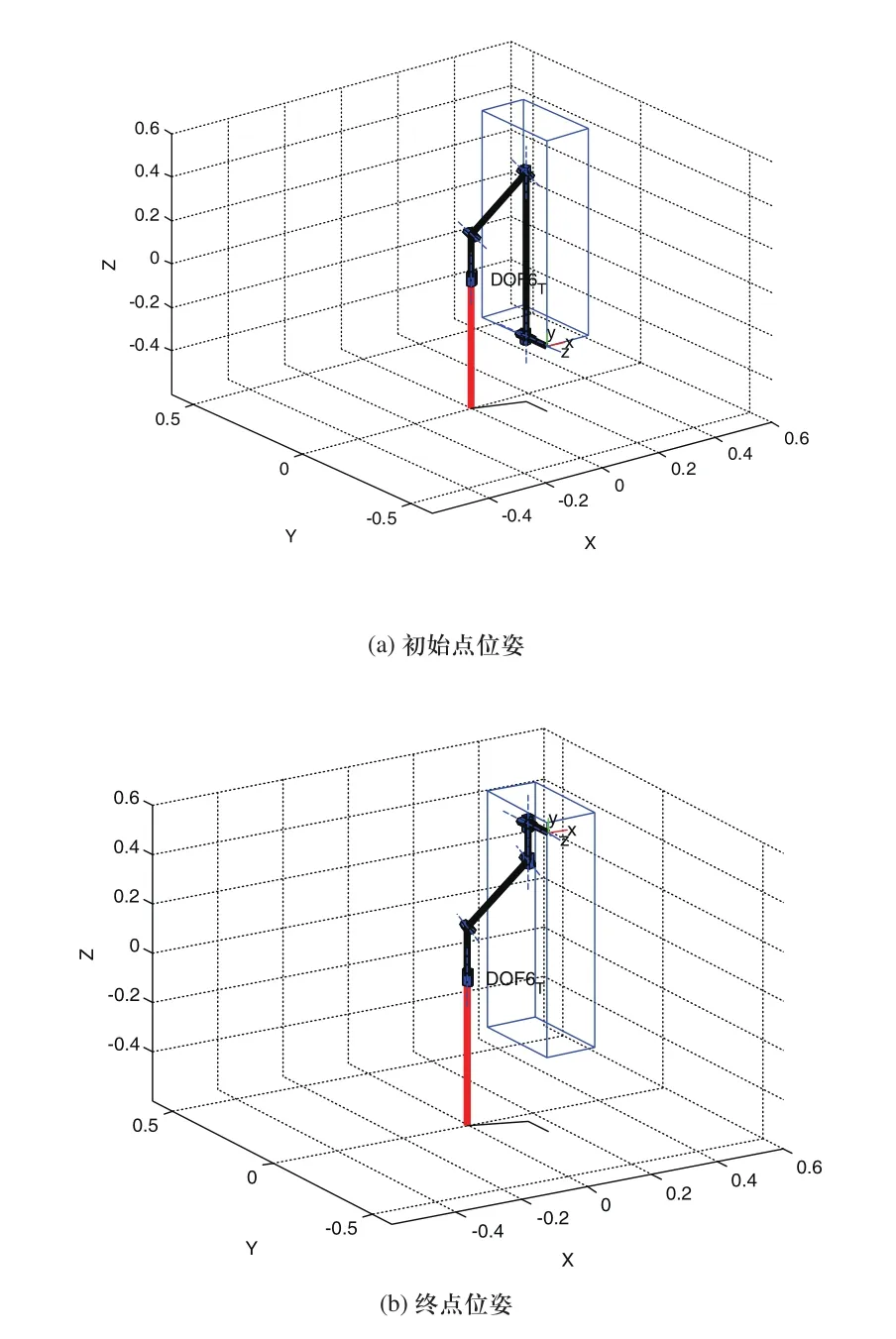
圖6 箱體焊接仿真

仿真動作從底部（焊接起始點坐標X=-0.155，Y=-0.148，Z=-0.3）如圖6(a)所示，向頂部（終止點坐標X=-0.155，Y=-0.148，Z=0.6）如圖6(b)所示，焊接一條豎直的直線（插補間隔Z=0.05）逆解數據表如表5所示。

在箱體的底部機器人關節逆解為表5中第一行數據，在箱體頂部機器人6個關節的逆解為表3中最后一行數據。通過關節數據對比發現只有的d4值發生了變化，其他的關節值沒有發生變化，因此焊接此條豎直焊縫是只有第四軸平移軸在運動。逆解表能夠充分的說明在焊接類似的豎直焊縫時機器人的第四個關節只需要平移就可以完成，其他的關節不需要運動，但是在運動之前需要機器人首先將各個關節的角度調整到一定的角度。另外，焊接過程中不需要其他的關節運動，說明該機器人能夠解決通用6-DOF機器人的奇異位姿不能到達的問題。

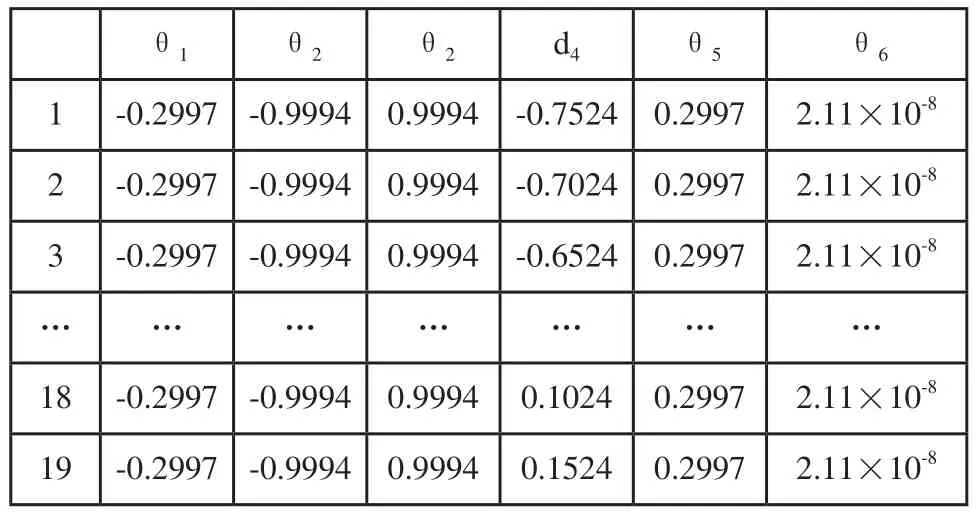
表5 逆解數據表

5 結論

本文提出了一種新型的機器人結構，此結構機器人由于第四軸為平移軸，一定程度上有效的避免了奇異位姿導致的無解和機器人自由度退化等問題。同時由于第四軸為平移軸，若采用高精度絲桿，可以大大的增加直線運動的軌跡精度，在未來的激光跟蹤焊接中，焊接軌跡精度可達到0.001mm。另外，此機器人在焊接箱體結構的工件時，尤其是焊接直線時由6軸聯動變為單軸運動，大大的降低了機器人的能耗。本機器人預計將在超高精度焊接領域發揮重要作用。

[1]潘磊,錢煒,張志艷,祁秋艷, PanLei, & QianWei等.四自由度機械臂運動學分析及matlab仿真[J].機械科學與技術,2013.32(3),115-119.

[2]劉晶晶,彭俊泉,劉新華.基于MATLAB的串并混聯7-DOF仿人機械臂正運動學分析及仿真[J].機械傳動,2015(7):59-62.

[3]熊有倫,唐立辛,丁漢.機器人技術基礎[M].武漢:華中科技大學出版社,2008:8-200.

[4]Seling J M.機器人學的幾何基礎[M].北京:清華大學出版社,2008:150-200.

[5]JOHN J.CRAIG[美].機器人學導論:第3版[M].機械工業出版社,2006.

[6]Peter Corke.Robotics,Vision and Control[M].Berlin:Springer-Verlag Berlin and Heidelberg,2001:50-128.

[7]林義忠,歐爽翔.六自由度焊接機器人本體結構設計及動力學仿真[J].機械設計與制造,2014.6,21-23.

[8]劉 鵬,宋濤,贠超,高志慧.焊接機器人運動學分析及軌跡規劃研究[J].機電工程,2013,290-294.

[9]鄔亞蘭.焊接機器人的軌跡規劃與仿真研究[D].合肥:合肥工業大學,2011.

[10]盧銳,王忠慶.基于MATLAB Robotics Tools的機械臂仿真[J].電子世界,2014(18):417-418.