改進粒子群算法對鋼卷混流包裝線平衡問題的研究

王 強，張含葉，王 利

（1.九江學院 機械與材料工程學院，九江 332005；2.九江學院 教務處，九江 332005）

0 引言

鋼卷的品種和數量隨顧客需求的變化而變化，在最短的時間內，應該能最大限度地滿足不同客戶的個性化需求。鋼卷的混流包裝線能夠適應多品種生產的需要，在基本不改變現有生產手段、生產條件和生產能力的前提下，通過改變生產組織方式，在一定的時間內，在同一條包裝生產線上包裝出不同代碼的多品種鋼卷產品。因此，鋼卷混流包裝生產線能夠快速響應市場需求的變化，節約流動資金，降低成本，提高產品的競爭力。

混流包裝生產線平衡問題屬于NP-Hard問題[1]，采用傳統的精確方法求解比較困難。隨著科技的發展，許多人工智能方法被用來求解混流裝配線平衡問題，例如：遺傳算法[2～7]、蜂群算法[8,9]、蟻群算法[10～14]、差分進化算法[15]等。本文采用改進粒子群算法對對混流鋼卷包裝線平衡問題進行研究。

1 問題描述

混流鋼卷包裝線平衡問題可以描述為：在計劃期內，在同一包裝線上混合連續地包裝M種系列產品的鋼卷，這M種鋼卷結構相似、工藝相近，每個品種鋼卷的包裝由若干任務組成，這些任務都有嚴格的順序要求，產品包裝中任務之間的關系可以用作業順序圖來描述。

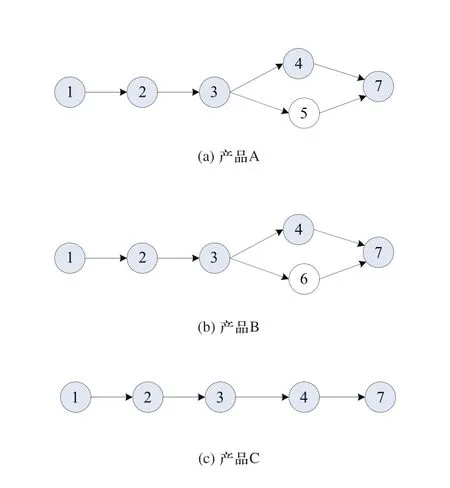
圖1 裝配優先關系圖

圖1為三種產品A、B和C的裝配優先關系圖，因為不同品種產品的裝配優先關系圖之間存在差異，所以在研究混流產品裝配線平衡問題時，常用的方法是將其合并為一個綜合裝配優先關系圖，如圖2所示。

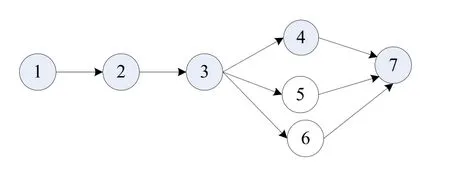
圖2 綜合裝配優先關系圖

2 數學模型

2.1 變量定義

本文用到的變量及其含義如表1所示。

2.2 目標函數

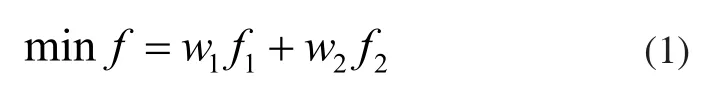
其中：

w1和w2均為權重系數。

2.3 約束條件

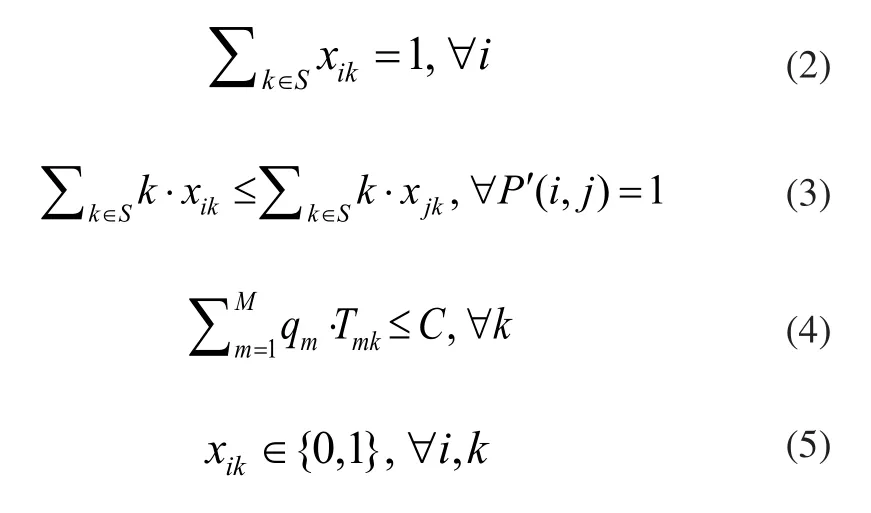
其中，式(2)確保任一作業元素只能分配到某一工作站中；式(3)為裝配優先關系約束；式(4)為節拍約束；式(5)表示變量的取值范圍。

表1 變量定義

3 算法設計

3.1 基本粒子群算法

在每一代，粒子Xα的速度和位置更新公式分別為：

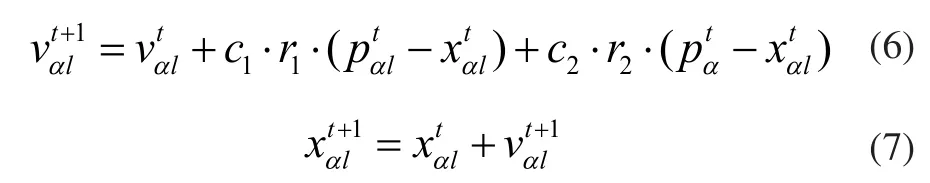
式(6)中右邊第一項為粒子先前速度的繼承；第二項為“認知”部分，是一個增強學習過程；第三項為“社會”部分，表示粒子間的信息共享與相互合作。在搜索過程中粒子一方面記憶它們自己的經驗，同時考慮其同伴的經驗。當單個粒子覺察同伴經驗較好的時候，它將進行適應性的調整，尋求一致認知過程。

3.2 改進粒子群算法

對式(6)進行改進，改進后的粒子群算法如下：

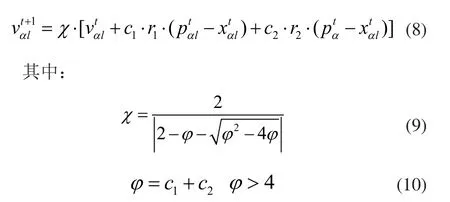
改進粒子群算法的流程如下：

Step 1：確定參數：種群規模PS、加速常數c1和c2、權重系數w1和w2、最大迭代次數Tmax；

Step 2：產生初始種群；

Step 3：根據式(1)和約束條件(2)～(5)，計算適應度函數；

Step 5：判斷是否滿足終止條件（本文以迭代次數是否達到預設的代數Tmax作為終止條件），如果滿足，則進入Step 6；否則，轉入Step 2；

Step 6：輸出最優解，算法結束。

4 實例求解

已知Z企業[16]現有的多條包裝生產線均為單一品種包裝生產線，由于各種產品需求量相差較大，表現在包裝生產線上就是各條線有忙有閑，工作負荷分布不均，為了提高包裝生產線的利用率，有必要引入混流包裝生產線。通過調研發現A、B兩種鋼卷產品結構相似、工藝相近，因此對其混流包裝生產線進行優化設計，其綜合作業優先關系圖和作業元素時間分別如圖3和表2所示。

該企業一天的生產時間為8小時，采用兩班制，即57600秒。根據需求量的要求，包裝線每天至少生產產品480個。兩種產品包裝數量占總包裝數量的比例分別為qA=2/3，qB=1/3，則初始生產節拍為C=57600/480=120秒。

[17]，將改進粒子群算法中的參數設置如下：PS=80，c1=c2=2.05，w1=10，w2=1，Tmax=100。將c1=c2=2.05代入式(10)和式(9)得：?=4.1，χ=0.7298。

根據第3節中的求解流程，采用MATLAB軟件對其進行編程求解，結果如表3所示。

則該鋼卷混流包裝線的平衡率為：

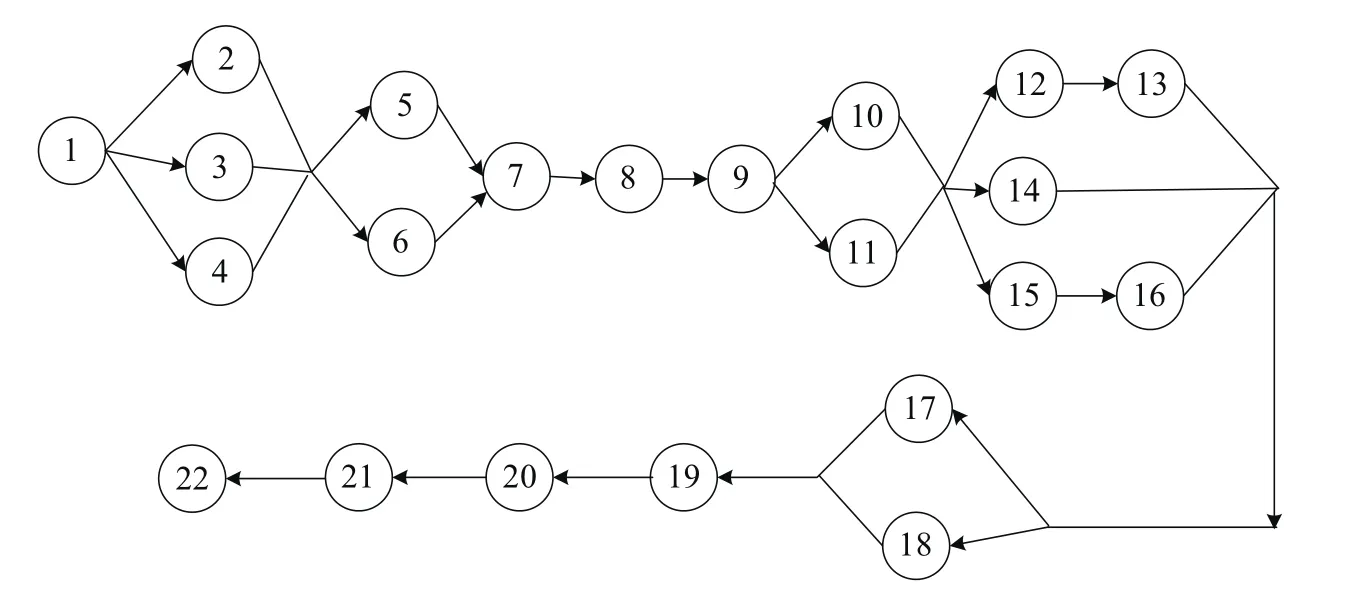
圖3 產品A和產品B的綜合作業優先關系圖

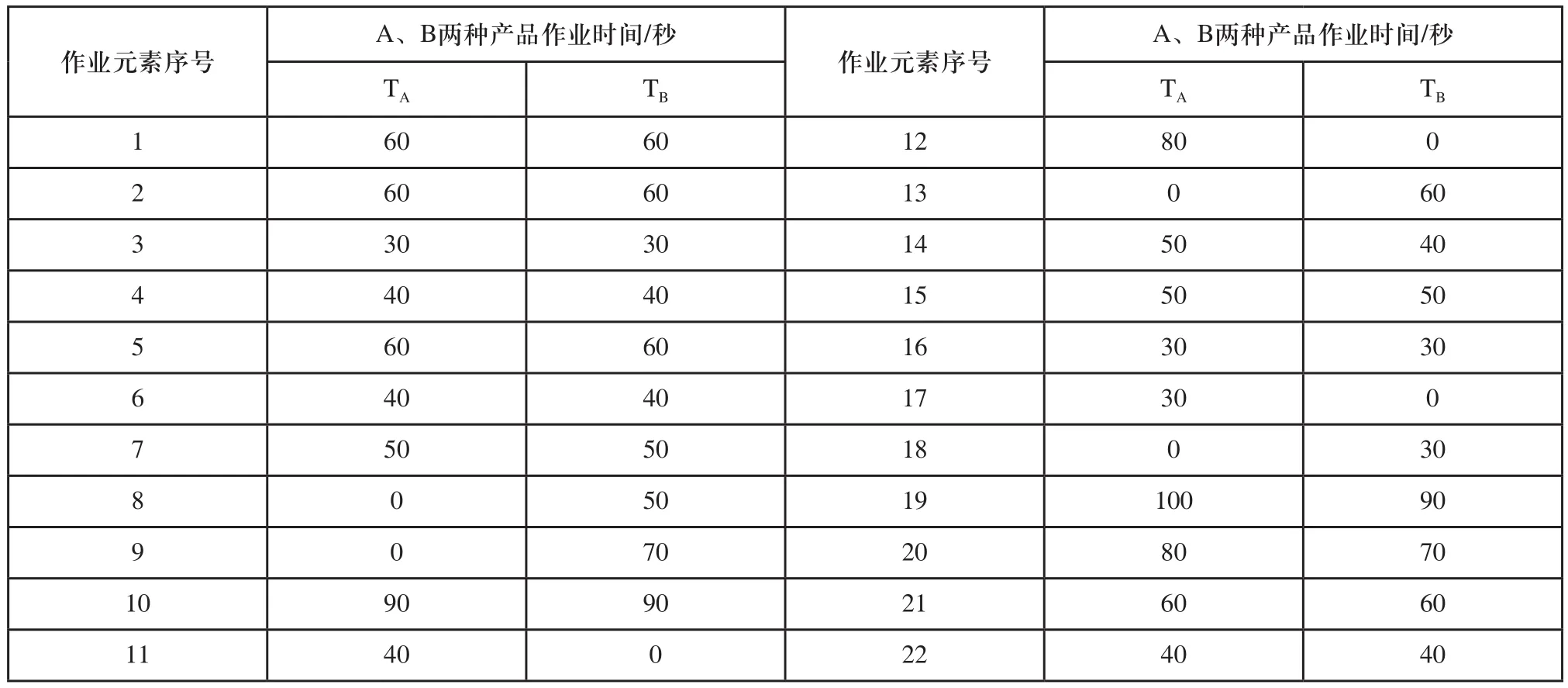
表2 產品A和產品B的作業元素作業時間

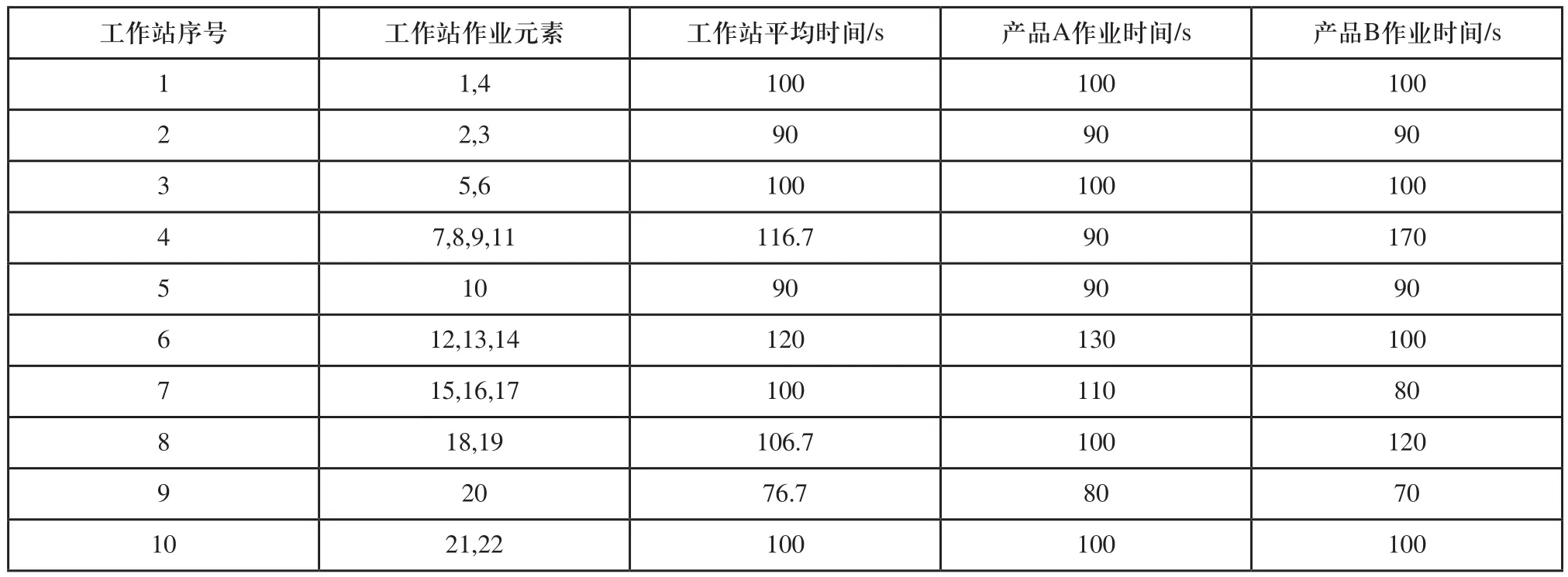
表3 鋼卷包裝生產線平衡結果

由此可以看出，采用改進粒子群算法求解鋼卷混流包裝線平衡問題取得了較好的平衡效果。

5 結束語

針對鋼卷混流包裝生產線的平衡問題，以工作站數和各工作站作業時間均方差的線性組合最小化為目標函數，采用改進粒子群算法對其進行求解，結果表明改進粒子群算法可以有效地求解鋼卷混流包裝生產線的平衡問題。

參考文獻：

[1]苑明海,李東波,于敏建.面向大規模定制的混流裝配線平衡研究[J].計算機集成制造系統,2008,14(1):79-83.

[2]TANG Q H, LIANG Y L, ZHANG L P, et al. Balancing mixedmodel assembly lines with sequence-dependent tasks via hybrid genetic algorithm[J].Journal of Global Optimization, 2016,65(1):83-107.

[3]HAQ A N, RENGARAJAN K, JAYAPRAKASH J.A hybrid genetic algorithm approach to mixed-model assembly line balancing[J]. International Journal of Advanced Manufacturing Technology, 2006, 28(3-4): 337-341.

[4]TIACCI L, SAETTA S, MARTINI A. Balancing mixed-model assembly lines with parallel workstations through a genetic algorithm approach[J]. International Journal of Industrial Engineering:Theory Applications and Practice,2006,13(4):402-411.

[5]MAMUN A A, KHALED A A, ALI S M, et al. A heuristic approach for balancing mixed-model assembly line of type i using genetic algorithm[J].International Journal of Production Research,2012, 50(18): 5106-5116.

[6]YU JF, YINYH. Assembly line balancing based on an adaptive genetic algorithm[J].International journal of advanced manufacturing technology,2010,48(1-4):347-354.

[7]AKPINAR S, BAYHAN G M. A hybrid genetic algorithm for mixed model assembly line balancing problem with parallel workstations and zoning constraints[J].Engineering applications of artificial intelligence,2011,24(3): 449-457.

[8]YUAN B, ZHANG C Y, SHAO X Y, et al. An effective hybrid honey bee mating optimization algorithm for balancing mixedmodel two-sided assembly lines[J].Computers and Operations Research,2015,53:32-41.

[9]SAIF U, GUAN Z L, LIU W Q, et al. Multi-objective artificial bee colony algorithm for simultaneous sequencing and balancing of mixed model assembly line[J].International journal of advanced manufacturing technology,2014, 75(9-12):1809-1827.

[10]AKPINAR S, BAYHAN G M. Performance evaluation of ant colony optimization-based solution strategies on the mixed-model assembly line balancing problem[J].Engineering Optimization,2014,46(6):842-862.

[11]AKPINAR S, MIRAC B G, BAYKASOGLU A.Hybridizing ant colony optimization via genetic algorithm for mixed-model assembly line balancing problem with sequence dependent setup times between tasks[J].Applied Soft Computing Journal, 2013,13(1):574-589.

[12]YAGMAHAN B.Mixed-model assembly line balancing using a multi-objective ant colony optimization approach[J].Expert Systems with Applications. 2011, 38(10):12453-12461.

[13]ZHANG Z Q,CHENG W M,ZHONG B, et al. Hybrid behavior ant colony optimization for mixed-model assembly line balancing problem[J].Journal of Mechanical Engineering,2009,45(5):95-101.

[14]Blum C. Beam-ACO for Simple Assembly Line Balancing[J].Informs journal on computing, 2008, 20(4): 618-627.

[15]ZHANG X M, HAN X C. The Balance Problem Solving of the Car Mixed-model Assembly Line Based on Improved Differential Evolution Algorithm[J].Applied Mechanics and Materials, 2012(220-223):178-183.

[16]劉海江.寶發展鋼產品包裝工藝技術報告[R].上海:同濟大學現代制造技術研究所,2012.

[17]段曉東,王存睿,劉向東.粒子群算法及其應用[M].沈陽:遼寧大學出版社,2007.