基于遞推相關運算的電容投切過零點檢測方法研究

許巧云，王碩君，韓 冰，董超俊，顏世才

（1.江門供電局，江門 529020；2.五邑大學，江門 529020）

0 引言

電力系統中，電容器組投切時會產生涌流及過電壓，從而對電容器造成危害，使其過早損壞，此外在電容器組投切過程中所引起的暫態過程還會造成電網設備絕緣惡化、電能質量下降、干擾靈敏度高的電氣設備正常工作等問題[1]。電容器投切產生涌流的大小與開關關合時電壓的相位有關。電容器組的過零選相投切，可減小電容器合閘涌流[2]。某供電局為監測斷路器合閘過程對電容器造成的影響，在變電站的實時運行數據基礎上，進行分相投切實驗，需要確定過零點時刻的相位。過零點檢測是許多電力系統設備，儀器儀表必須具備的功能之一。目前市場上已經出現的成熟產品，基本方法是通過對測試信號進行濾波處理，在過零點附近采用一些算法處理（例如相位積分法[3]、半波傅氏方法[4]、過零點附近采用信號的插值算法計算過零點時刻[5]、利用相角差計算頻率[6]、一元線性回歸[7]等方式）判別過零點的實際時刻。有的是采用硬件過零比較器來實現[8～10]，但是這種方法電路復雜，比較器需要雙電源才能實現過零信號的檢測。在實際的工程中，電力系統中存在各種諧波和噪聲的干擾，導致過零點檢測不準確，精度較低。

針對上述檢測方法存在的問題，本文基于某變電站實時運行數據，采用遞推相關運算法來檢測零點，確定分相投切的相位。首先建立電網運行的仿真模型，對電壓信號進行數據采集，并模擬工程信號，在采集得到的信號加入高斯噪聲；然后將原始信號與標準50Hz余弦信號進行相關運算；最后，通過計算截取信號的初相角，推算過零點的時刻。遞推相關運算法來檢測零點，可將高次諧波和測試系統中存在的高斯噪聲濾除，且算法結構簡單，過零點的檢測精度較高。

1 理論分析

設電網的工頻為f0=50Hz。根據電力系統實際運行情況，則電網采集得到的電壓信號為U(t)：

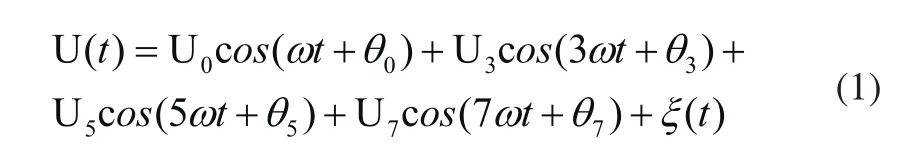
式(1)中U0為電網最大值，ω=2πf0，θ0為采集到信號的初相。U3，U5，U7分別為三次，五次，七次諧波的最大值。θ3，θ5，θ7分別為三次，五次，七次諧波的初相。為存在于測試系統中的高斯噪聲。

對電壓信號U(t)隨機截取50個周期，即截取信號時間的長度為1s。在運算程序中生成標準余弦信號，標準余弦信號與采集得到的信號進行相關計算，則可得到計算結果為A(t)：

對式(2)積分式進行簡化：

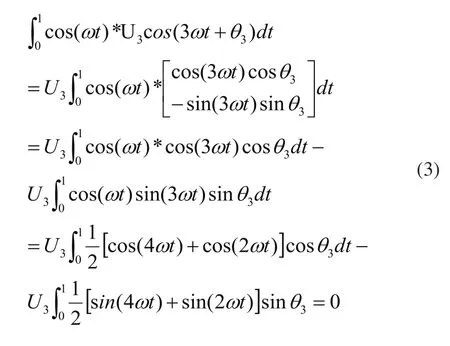
由式(3)可知三次諧波與基波的卷積值為0，三次諧波與基波是是正交的。同理五次和七次諧波與基波是正交的，積分值也將為零。高斯噪聲與基波是正交的，即積分的值也將是零。式(2)只有第一項積分值不為零。對第一項積分進行簡化運算得：

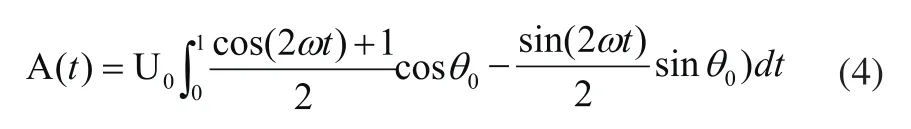
當式(4)中對50個整周期進行積分時，含有2倍基波項的積分值將為零。假設U0為已知的，則計算的值將是關于初相θ0的函數，如式(5)和式(6)：

通過相關運算可以計算截取時刻的初相為角θ0。由于電網運行的工作周期是定值0.02s，且一個周期有兩個過零點。截取信號的時刻設為t0，則相關運算過零點存在于t00：

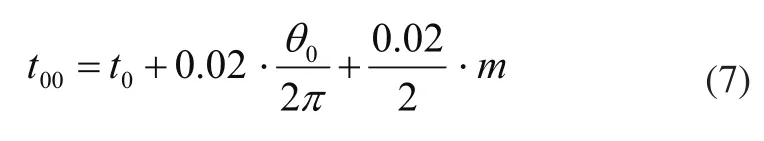
式(7)中的m為自然數。

2 相關分析過程

圖1為相關運算流程圖。在檢測過程中首先得到測量電網運行電壓信號，并隨機截取50個周期的時間長度與標準的正弦進行相關運算，得到截取信號的初相角θ0，從而通過式(7)得到過零點時刻。

圖1 相關運算流程圖

通過圖1的流程圖過程可以得到精度較高的過零點時刻。

3 10kV變電站模型的建立

在PSCAD仿真軟件中電源采用Three-Phase Voltage Source Model 2模型。兩臺變壓器參數均根據某變電站銘牌數據進行設定，在PSCAD仿真軟件中110kV/10kV和10kV/0.4kV兩臺變壓器均采用3-Phase 2-Winding Transformer模型。仿真模型中負載數據均根據供電局實測數據進行設定。在仿真過程中加入三個諧波電流源。分別為三次諧波電流源為0.0025kA，五次諧波電流源為0.0015kA，七次諧波電流源為0.001kA。

4 仿真結果的分析

4.1 仿真實測數據

江門某變電站在實際運行系統中存在有高次諧波。在仿真過程中為了清楚的顯示高次諧波的存在，加入了超額度的諧波含量。在PSCAD仿真系統中加入三、五、七次諧波電流源之后，測的電壓數據如圖3所示。圖3(a)是整體顯示，圖3(b)是圖3(a)的局部顯示。

考慮到實際的工程中實測信號會有噪聲分量。用PSCAD程序生成高斯噪聲（用程序生成范圍為±0.6的隨機數作為高斯噪聲），疊加到所檢測的信號中，得到的信號如圖4所示。圖4(a)是整體顯示，圖4(b)是圖4(a)的局部顯示。

圖3 電壓數據圖

4.2 仿真結果的計算

4.2.1 第一組實驗過程

在實驗過程中，隨機截圖如圖4(a)所示的信號，截取長度為50個周期。通過流程圖1相關算法計算出過零點。隨機截取第一組數據，得到信號如圖5所示。

通過式(5)的計算計算出初相角的余弦值為-0.314，通過式(6)進行反余弦計算，得到初相角為-146.8度。而實際的初相角為-148.5度（實驗系統為已知系統），誤差為1.7度。采用式(7)，計算得到過零點時刻，即誤差為1.7度。

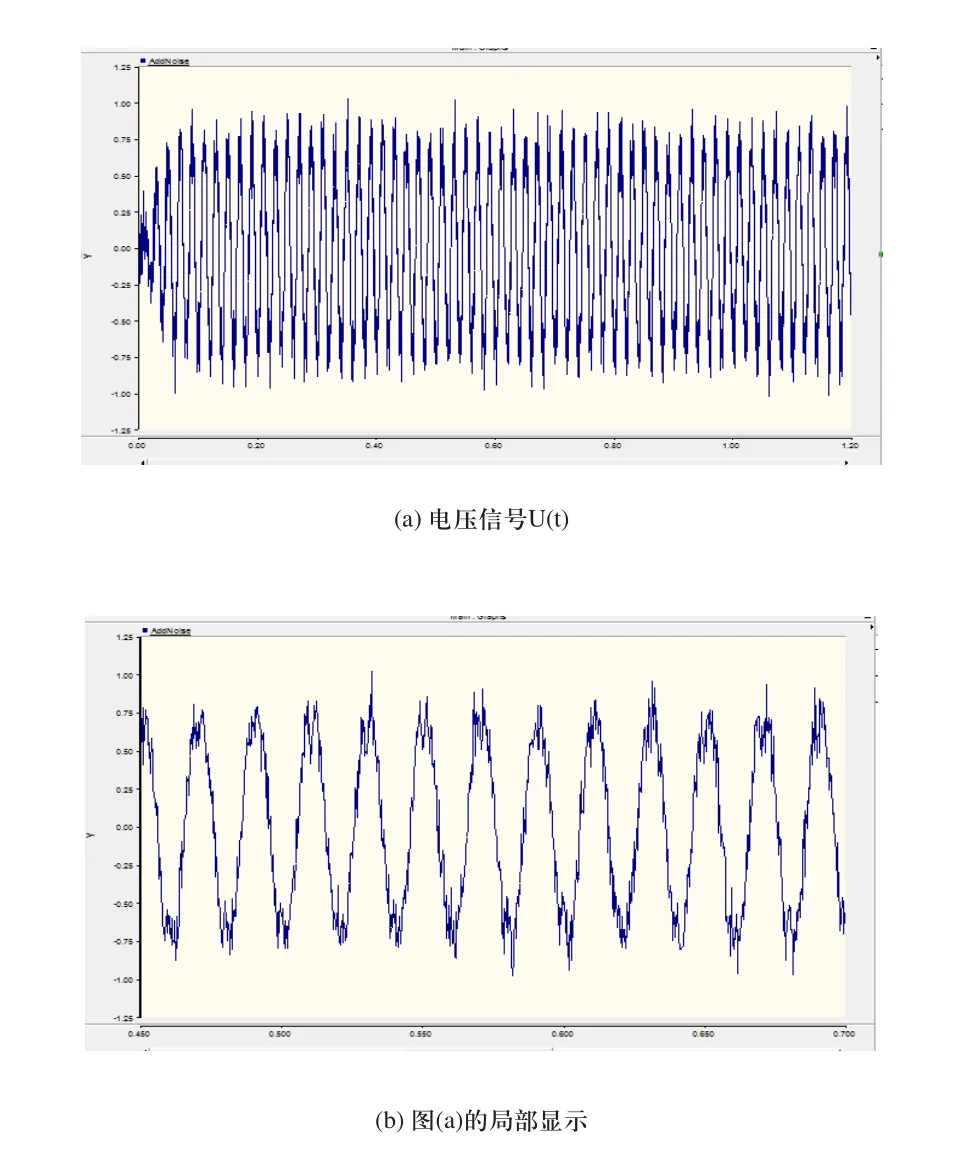
圖4 疊加噪聲后的電壓數據圖

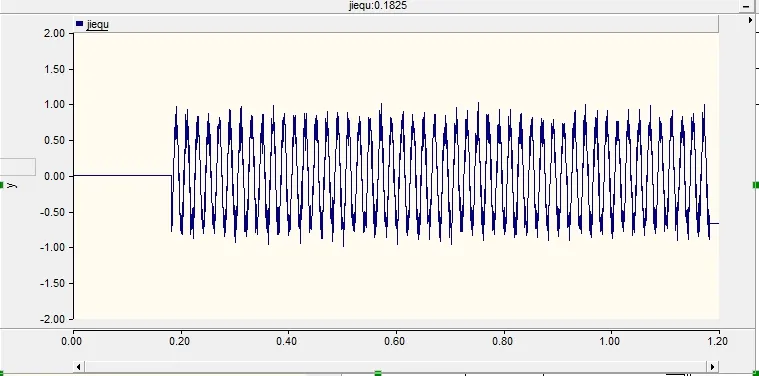
圖5 第一組截取信號

4.2.2 第二組實驗過程

隨機截取另外50個周期信號，得到圖6所示的數據。通過流程圖1相關分析的算法計算出過零點。通過(5)式的計算，計算出初相角的余弦值為0.1918。通過式(6)進行反余弦，計算得出截取信號初相為-59.55度。而實際的余弦值為-58.5度。誤差為1.05度。采用式(7)，計算得到過零點時刻，即誤差為1.05度。

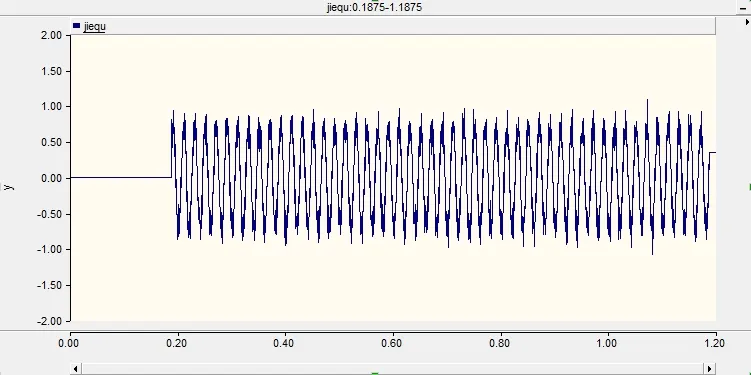
圖6 第二組截取信號

4.2.3 第三組實驗過程

隨機截取第三組50個周期信號，得到如圖7的數據。通過流程圖1相關分析的算法計算出過零點。通過式(5)的計算，計算出初相角的余弦值為-0.0875，通過式(6)反余弦，計算得到截取信號的初相為103.4度。而實際的余弦值為103.5度。誤差為0.1度。采用式(7)，計算得到過零點時刻，即誤差為0.1度。

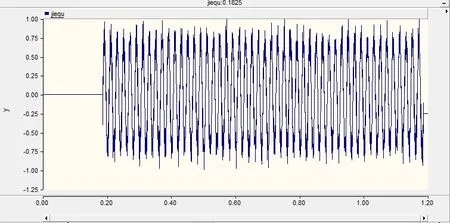
圖7 第三組截取信號

為了驗證試驗結果具有普遍意義，共做32組實驗，得到的實驗結果如表1所示。表中顯示隨機截取32組試驗數據，通過實際的初相角與計算的得到的初相角比較，獲得相關分析計算偏差。

5 結束語

在電網工頻為50Hz不變的情況下，通過隨機的截取50個周期的信號，通過與標準余弦信號進行相關運算，計算得出截取信號的初相角。實驗結果表明該算法得到初相角偏差小于2度，即過零點偏差小于0.1μs。綜上所述，采用相關運算處理機的結構簡單，過零點檢測中可以達到很高的精度，在相控斷路器系統中能夠得到應用。然而在實際的系統中系統的工頻存±0.1Hz的誤差，解決工頻誤差的問題需要進一步的探究，提高過零檢測的精度。

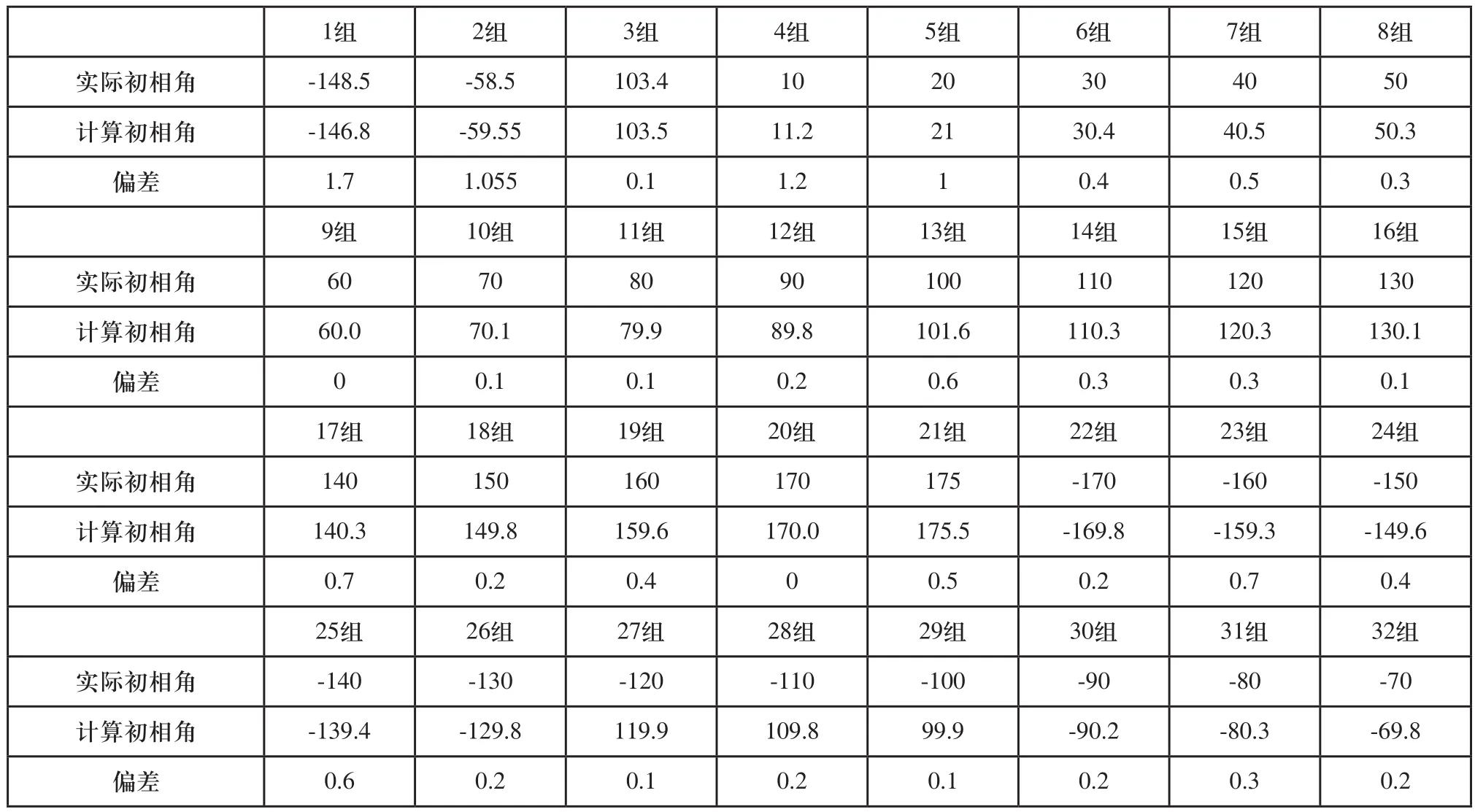
表1 數據的實驗結果

[1]吳世寶,王亮,徐建源,等.真空斷路器同步關合控制中電壓過零點檢測裝置[A].2010電工測試技術學術交流會論文集[C].武漢,2010:162-164.

[2]丁富華.真空開關的選相控制及其應用研究[D].大連理工大學,2006.

[3]陳誠,戴爾晗,馬亞男.基于過零點檢測方法的改進研究[J].微型機與應用,2016,35(20):79-81.

[4]劉紅星.基于真空斷路器選相控制過零點檢測的研究[J].電氣技術,2016(9):51-54,58-59.

[5]R.W. Wall. Simple Methods for Detecting Zero Crossing Industrial Electronics Society[A].IECON’03.The 29th Annual Conference of the IEEE[C],2003.

[6]Wang Maohai,Sun Yuanzhang.A practical method to improve phasor and power measurement accuracy of DFT algorithm[J].IEEE Trans on Power Delivery,2006,21(3):1054-1062．

[7]易龍強.基于一元線性回歸理論的數字正弦信號頻率測量算法[J].電測與儀表,2011(3):20-24.

[8]尤進強.交流電源過零點檢測新方法及運用實踐微探[J].工業技術,2017(1):82-83.

[9]李鳴華,余水寶.基于過零點的信號分析與檢測[J].儀器儀表學報,2004(8),64-65.

[10]Zhipeng Chen and Zhaohui Li.Robust Precise Time Difference Estimation Based on Digital Zero-Crossing Detection Algorithm[A].IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission[C],2016.