一種新的房顫心電特征提取方法

張 瑞，楊宇峰，孫亞楠

(西北大學 醫學大數據研究中心, 陜西 西安 710127)

房顫,又稱心房顫動,是臨床上最常見的心律失常。房顫的發作是由于心房肌喪失了正常有規律的收縮活動,而代之以快速不規則的房顫波,發作時患者通常會有心悸、乏力、眩暈等癥狀,嚴重者可誘發或加重心力衰竭,甚至引起腦卒中[1-2]。心電圖(Electrocardiogram,ECG)是由心電圖儀記錄反映心臟興奮的電活動過程,對房顫的診斷與治療具有重要的參考價值[3]。圖1顯示一個正常心動周期內的心電圖波形,其中P波表示心房去極化過程,QRS復合波表示心室去極化過程,T波表示心室復極化過程[4]。而當陣發性房顫發作時,心房壁各部位出現雜亂無序的興奮,導致心臟無法正常收縮,在心電圖上通常表現為(見圖2):①P波消失,代之以大小不等、間隔不勻、形態不同的f波(也稱為房顫波,頻率在350～600次/分);②RR間期不規則且伴有心率過速[5]。

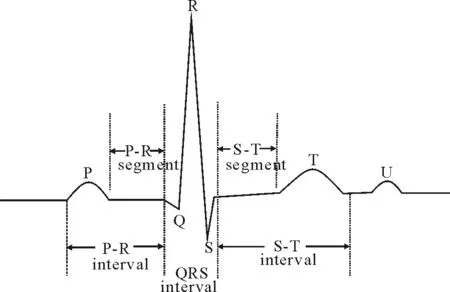
圖1 一個正常心動周期的心電圖波形Fig.1 ECG of a normal cycle

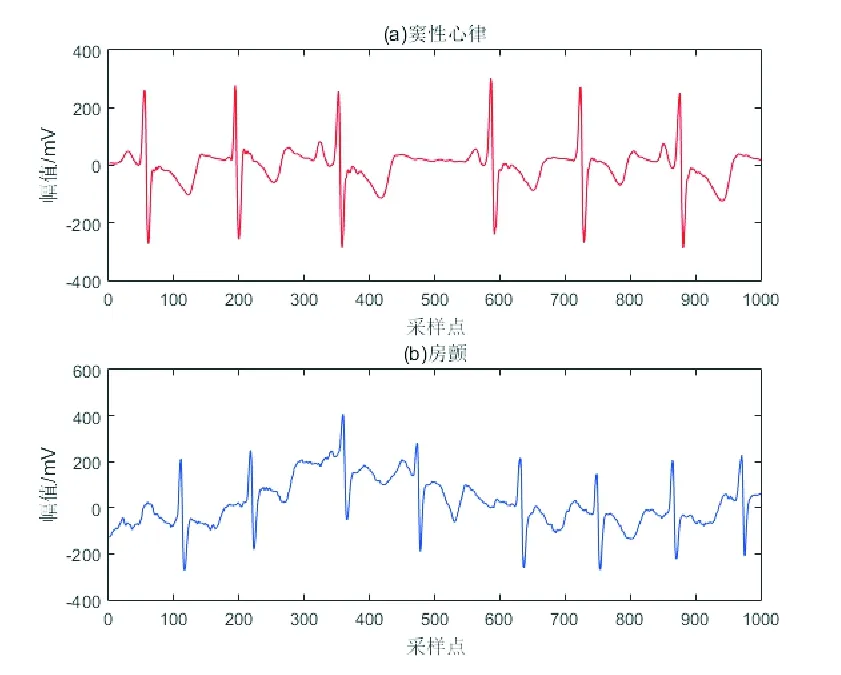
圖2 竇性心律與房顫心電Fig.2 Sinus rhythm and atrial fibrillation

根據房顫發作持續時長,可分為陣發性房顫、持續性房顫和永久性房顫。由于陣發性房顫發作突然且持續時間短暫,臨床上易被漏診,從而往往需要長時程的心電監測。隨之而產生的海量心電數據,使得醫生根據經驗進行視覺診斷這一傳統方法就變得十分耗時。此外,對于陣發性房顫在心電圖上所表現出的短暫且微弱的波形變化,僅依靠視覺觀察往往難以捕捉,從而造成較多漏診。因此,展開關于陣發性房顫自動檢測的研究具有十分重要的臨床意義。

近年來,陣發性房顫的自動檢測受到了越來越多研究者的關注。洛倫茲散點圖(Lorenz plot)作為信號在相空間上的幾何表示,能夠揭示心電信號中心率變異的非線性特征,因此被廣泛應用于房顫心電的特征提取[6-9]。文獻[10-11]中指出,心律失常狀態下的洛倫茲散點圖主要呈現魚雷形、短棒形、扇形、梭形和復雜形等,而竇性心律主要呈現彗星狀;Hargittai等人在文獻[12]中提出了dRR洛倫茲散點圖主要分析了早搏和房顫在該散點圖上的特征,其中房顫表現為不規則發散的圖形,早搏的圖形分為幾個明顯的群;Lian等人在文獻[13]中提出了RdR洛倫茲散點圖,并系統分析了房顫、室性早搏、二聯律、三聯律等心律失常在該散點圖上的表現特點;Chen等人在文獻[14]中采用三維洛倫茲散點圖進行刻畫并得出竇性心律呈現彗星狀,而心律失常則呈現漏斗、心形或不規則圖形等。上述方法均是通過刻畫RR間期的變化規律來提取特征,這就需要將R峰檢測作為預處理,使得最終的房顫檢測結果會直接受R峰檢測性能好壞的影響[15]。基于此,本文采用散點圖對原始心電信號直接刻畫,從中提取相應的度量指標以反映正常心電與房顫心電在散點圖上的表現差異,并將其融合作為房顫心電特征。最后,結合超限學習機(ELM)完成陣發性房顫的自動檢測,并在MIT-BIH心房顫動數據庫上驗證所提方法的有效性。

1 方 法

陣發性房顫的自動檢測本質上是一個模式識別問題。本小節首先介紹ECG信號的去噪過程;其次,從去噪后的ECG信號中提取恰當的房顫心電特征;最后,采用超限學習機完成陣發性房顫的自動檢測。

1.1 數據去噪

心電信號在采集過程中易受各種背景噪聲的干擾,主要包含工頻干擾、肌電干擾和基線漂移。本文分別采用50Hz陷波濾波器、35Hz低通數字濾波器及0.2Hz巴特沃茲高通濾波器,去除工頻干擾、肌電干擾及基線漂移。圖3顯示了一個心電信號片段(時長4s)去噪前后的效果。

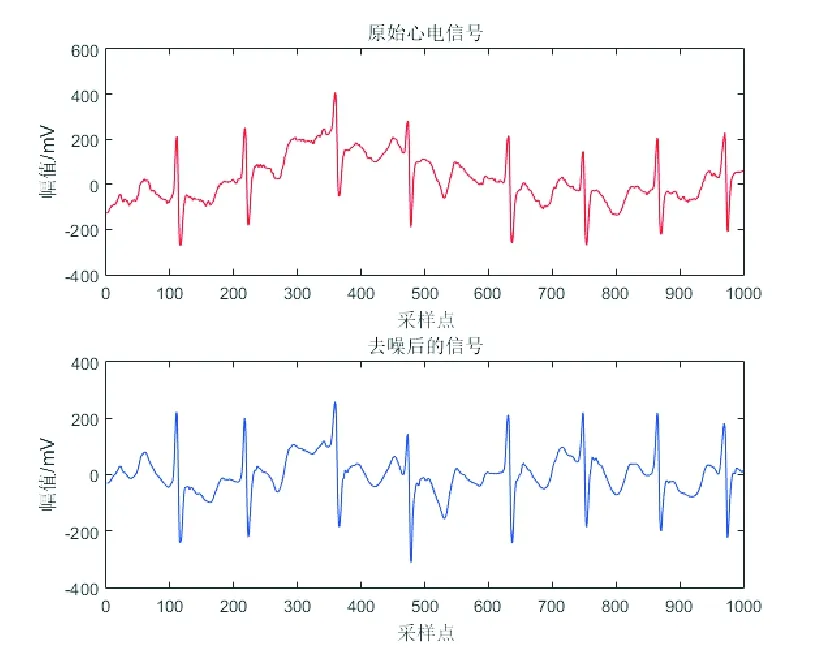
圖3 心電信號的去噪效果Fig.3 The performance of ECG denoising

1.2 特征提取方法

給定心電信號S={s(1),s(2),…,s(N)}。其中N表示心電信號的長度。圖4為正常心電和房顫心電所對應的散點圖。從圖中可以看出,相比于正常心電的散點圖,房顫心電的散點圖中分布在左下方區域、右上方區域以及偏離y=x軸的散點較多,分布較為分散。因此本文采用3個度量指標來刻畫其散度差異,并作為信號S的房顫心電特征。本文所提特征提取方法總結如下:

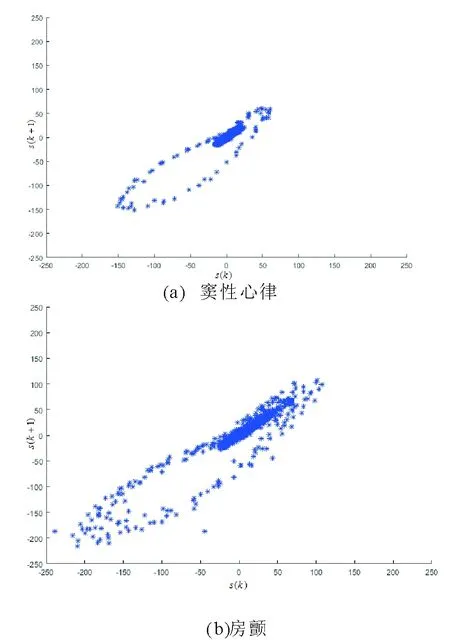
圖4 竇性心律、房顫發作時對應的散點圖Fig.4 The corresponding scatter diagramof sinus rhythm and atrial fibrillation

步驟1將信號S劃分為M個等長的心電片段Si={si(1),si(2),…,si(n)},i=1,2,…,M。

步驟2刻畫心電片段Si在坐標軸XOY上的散點圖(見圖4),并記為

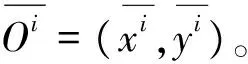
圖5 散點圖對應的98%的置信橢圓Fig.5 98% confidence ellipse corresponding to the scatter graph

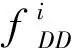
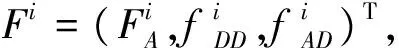
F=(F1T,F2T,…,FMT)

即構成了信號S的融合特征。

1.3 超限學習機

超限學習機是2006年由Huang等人提出的一種新的快速學習算法[16]。相對于傳統的學習算法, ELM具有學習速度快、無需迭代調整隱變量等優點,已被廣泛應用于各種分類和回歸問題。

其中Wi=(wi1,wi2, …,win)T為連接輸入層與第i個隱單元的權重向量,βi為連接第i個隱單元和輸出層的權重向量,bi是第i個隱層單元的閾值,Wi·Xj為Wi和Xj的內積。當網絡的實際輸出等于期望輸出時,則有

在ELM運算過程中,隱層輸入權重Wi和閾值bi隨機確定,則隱層輸出矩陣H被唯一確定。這樣,神經網絡中的訓練問題即轉化為求解線性方程組

Hβ=T

其中

H=

β=(β1,β2,…,βS)T，T=(t1,t2,…,tN)T。

2 數值實驗及結果分析

本小節采用MIT-BIH房顫數據庫中的部分心電記錄來驗證本文所提方法的可行性與有效性。

2.1 心電數據

本文使用的心電信號均來自于MIT-BIH心房顫動數據庫,該數據庫共包含25個心電記錄,采樣率為250Hz分辨率為12bit[17-18]。本文從中隨機選用6個時長為1h的心電記錄進行數值實驗,所有實驗均在Matlab R2016b中運行。

2.2 實驗結果與分析

本文采用50Hz陷波濾波器、35Hz低通數字濾波器及0.2Hz巴特沃茲高通濾波器對原始心電信號進行去噪,并將去噪后的心電信號進行無重疊分段處理,每個心電片段長度為4s(1 000個采樣點)。在實驗過程中,所有數據被隨機均分為訓練集和測試集。為了降低隨機均分所導致的訓練集和測試集中不同類數據點的不均衡,本文將這種隨機均分的實驗執行50次,并取50次實驗的平均結果作為最終分類性能的度量。

在構建置信橢圓時,本文采用ROC曲線實現最佳置信參數U%的選取。圖6為參數U%從95%開始,按1%的步長增加至99%所得的ROC曲線。從圖6可以看出,當參數U%=98%時,ROC曲線下包圍的面積AUC最大,表明分類性能最好。

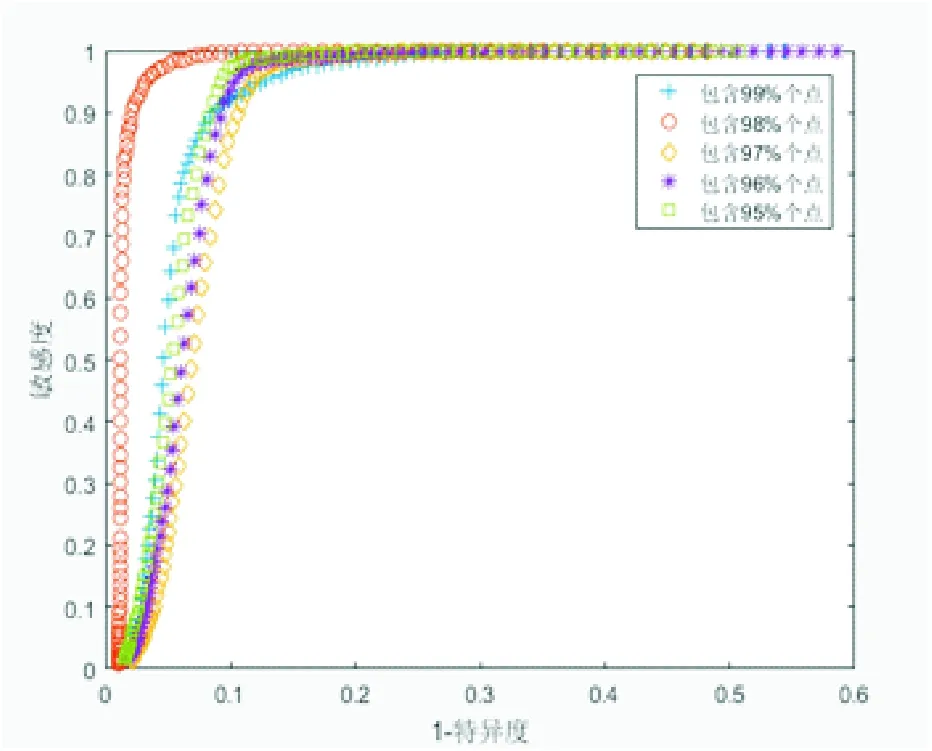
圖6 置信橢圓的參數選取Fig.6 Determination of parameter U

在ELM中,激活函數選取為Sigmoid函數,隱節點選取為可加型節點,并通過訓練準確率來確定最佳隱節點個數。圖7為采用混合數據進行訓練時,隱節點個數從5開始,以5為步長增加到50所對應的分類準確率。從圖7可以看出,當隱節點個數為40時,分類準確率可達到最大94.34%。

圖7 ELM 中不同隱節點在訓練集上的準確率Fig.7 Accuracy of different hidden nodes on training set in ELM

本文采用準確率(accuracy)、敏感度(sensitivity)以及特異度(specificity)作為評估算法的度量指標分別定義為:

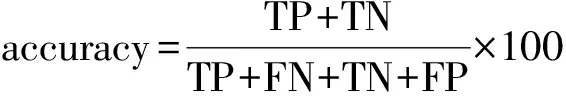
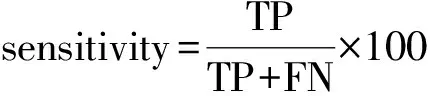
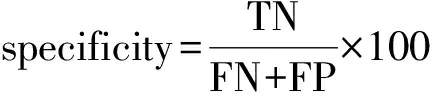
其中TP(true positive)為真陽性,表示實際為發作心電且被正確檢測為發作心電;FP(false positive)為假陽性,表示實際為正常心電卻被錯誤檢測為發作心電;TN(true negative)為真陰性,表示實際為正常心電且被正確檢測為正常心電。FN(false negative)為假陰性,表示實際為發作心電且被錯誤檢測為正常心電。

為了檢驗本文所提取融合特征的可行性與有效性,首先分別對6位病人進行個人5倍交叉驗證,即將每個患者的心電信號平均分為五等份,其中4/5用于訓練,1/5用于測試,進行五次后取其平均結果作為最終的分類性能指標,試驗結果如表1所示。從表1可以看出本文提出的基于融合特征的自動檢測方法對6個病人都具有較好的檢測效果,說明所提特征能夠很好地區分正常心電與房顫心電。

為了驗證本文所提取方法具有普適性,進一步對6位病人的數據進行混合檢驗,即將其中5個人的心電信號混合后作為訓練集,其余1個人的心電信號作為測試集,實驗結果如表2所示。從表2可以看出,此融合特征對于混合數據同樣有良好的檢測效果,說明此特征具有較高的普適性,能夠在臨床應用中有效實現陣發性房顫的自動檢測。對比表1和表2中的實驗結果,發現用混合數據的實驗結果低于個人數據的實驗結果,這是由不同患者間的個體差異所造成。

表1 個人5倍交叉驗證Tab.1 Personal 5 fold cross validation

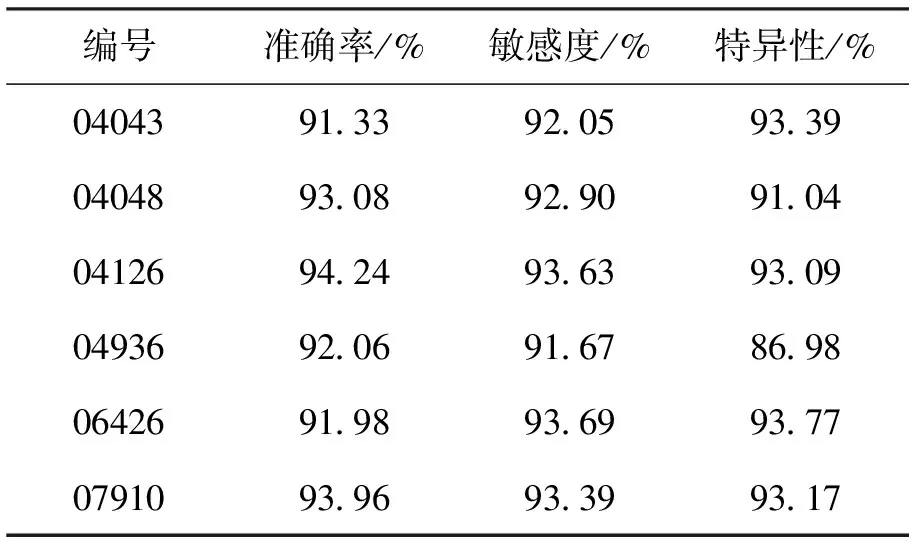
表2 混合數據檢驗Tab.2 Mixed data checking

3 結 論

本文提出了一種新的房顫心電特征提取方法。首先采用50Hz的陷波濾波器、35Hz的低通數字濾波器、0.2Hz巴特沃茲高通濾波器進行數據去噪,分別去除工頻干擾、肌電干擾和基線漂移;其次,將去噪后的心電信號分割成若干等長片段,繪制每個心電片段的散點圖,并計算散點圖的置信橢圓面積、置信距離散度和置信角散度進行融合作為心電特征;最終采用MIT-BIH房顫數據庫中的心電信號,結合超限學習機(ELM)完成陣發性房顫的自動檢測。數值實驗結果表明,本文所提出的陣發性房顫自動檢測方法具有較高的檢測性能,為臨床診斷提供一定的輔助作用。

[1] 陸悠，唐蓉蓉，毛家亮，等. 陣發性房顫、房撲的心電散點圖特征[J]. 臨床心電學雜志，2014, 23(4):271-273.

[2] 向晉濤.心電散點圖表達的心臟電生理現象[J].臨床心電學雜志, 2012, 21(1):6-10.

[3] LI C, ZHENG C, TAI C. Detection of ECG characteristic points using wavelet transforms[J]. IEEE transactions on bio-medical engineering,1995,42(1):21.

[4] 李方潔，沈紅軍，郭小玉，等.心房顫動伴短聯律間期寬QRS波散點圖的類型及特征[J]. 中國心臟起搏與心電生理雜志, 2011, 25(1):41-44.

[5] BRENNAN M, PALANISWAMI M, KAMEN P.Do existing measures of Poincare plot geometry reflect nonlinear features of heart rate variability? [J]. IEEE Transactions on Biomedical Engineering, 2001, 48(11):1342-1347.

[6] STRUMILLO P, RUTA J. Poincare mapping fordetecting abnormal dynamics of cardiac repolarization [J].Engineering in Medicine andBiology Magazine, 2002, 21(1):62-65.

[7] TSUBOI K, DEGUCHI A, HAGIWARA H. Relationship between heart rate variability using Lorenz plot and sleep level[C]∥Engineering in Medicine and Biology Society. IEEE,2010:5294.

[8] PARK J, LEE S, JEON M. Atrial fibrillation detection by heart rate variability in Poincareplot [J]. Bio Medical Engineering Online,2009,8(1):38.

[9] CONTRERAS P, CANETTI R, MIGLIARO ECorrelations between frequency-domain HRV indices and lagged Poincare plot width in healthy and diabetic subjects[J].Physiologicalmeasurement,2007, 28(1):85-94.

[10] WANG W, WEI Y, GUAN N, et al. The automaticdetectionand analysis of Electrocardiogram based on Lorenz plot[J].IEEE Proceedings of Robotics and Biomimetics.2016:644-649.

[11] 王恒迪，朱堅民，藺利峰，等. 洛倫茲散點圖及其在房顫自動診斷中的應用[J]. 生物醫學工程學雜志, 2007, 24(2):449-452.

[12] HARGITTAI S.Is it possible todetect atrial fibrillation by imply using RR intervals?[J].IEEE Proceedings of Computing in Cardiology, 2014:897-900.

[13] LIAN J, WANG L, MUESSIG D.A simplemethod todetect atrial fibrillation using RRintervals[J].American Journal of Cardiology,2011, 107 (10):1494-1497.

[14] CHEN L, ZHANG K, LIU K Q. Study on 3D Lorenz plots of heart rate variability[J].Nanoscience andNanotechnology Letters,2013, 5(2): 248-252.

[15] RUAN X, LIU C, LIU C,et al. Automatic detection ofatrial fibrillation using RR interval signal [C]∥International Conference on Biomedical Engineering and Informatics. IEEE, 2011, 28 (1):644-647.

[16] HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70:489-501.

[17] MOODY G B, MARK R G. The impact of the MIT-BIH arrhythmia database[J].IEEE Engineering in Medicine and Biology Magazine,2001,20(3):45-50.

[18] CASALEGGIO A. Differences on the correlation dimension of MIT-BIH ECG database recordings[J].Computers in Cardiology Conference,1993:539-542.