Delta機器人動力學建模與彈性誤差分析*

陳君杰，李攀磊，韓 威，許楊劍，王效貴

(浙江工業大學 機械工程學院，浙江 杭州 310014)

0 引 言

1985年，瑞士的Clavel[1]發明了Delta并聯機器人，該型機器人為三自由度空間平移機構，具有承載能力強、運動耦合弱、力控制容易等優點。隨著并聯機器人的應用領域不斷得到拓展，其工作環境日趨復雜，并聯機器人不斷向高速度、高加速度、高精度、重載荷和輕量化方向發展[2-3]，導致機構運行中彈性振動和運動誤差也隨之增加。傳統的剛體動力學分析方法無法滿足彈性誤差分析的需求，考慮構件彈性的動力學分析成了研究重點。通過運動彈性動力學分析方法(kineto-elasto-dynamic，KED)，將機構位移視作彈性位移與剛體位移(名義位移)的疊加，在給定機構名義運動條件規律的條件下，確定機構的彈性響應。

Piras[4]利用有限元理論與彈性動力分析方法(KED)研究了3-PRR平面并聯機器人的彈性動力學問題。劉善增等人[5]建立了剛柔耦合并聯機構系統的整體動力學方程的步驟與方法，對3-RRS并聯機器人的頻率特性進行了分析。韓亞峰等人[6]利用有限元理論，采用平面梁單元對Delta機器人進行了彈性動力學建模。Kuo等人[7]基于D-H方法定義了一組全局變量，在不使用約束方程的情況下，導出了Delta機器人的彈性動力學模型。目前，Delta并聯機器人的彈性動力學研究中大都認為其四邊形從動臂機構在運動過程中兩側桿保持平行，從而將其四邊形從動臂機構簡化為一根虛擬從動桿進行分析，而在實際運動過程中，由于驅動桿末端彈性轉角等影響，四邊形機構會產生扭曲，有必要針對機器人的四邊形機構進行動力學建模研究。

本研究將Delta機器人四邊形從動臂機構劃分為2剛性短桿與2柔性從動桿，通過分析其運動協調條件，在有限元理論基礎上建立Delta機器人的彈性動力學方程，通過數值方法求解出機器人在運動軌跡中的彈性誤差，并通過改變桿件截面尺寸，分析桿件截面尺寸對彈性誤差的影響。

1 彈性動力學方程

Delta并聯機器人結構圖如圖1所示。

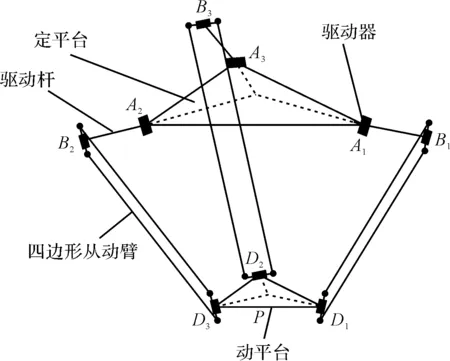
圖1 Delta并聯機器人結構圖

Delta機器人由定平臺、驅動器、驅動桿、四邊形從動臂、動平臺等組成，其中連接動平臺與定平臺的3個支鏈互成120°角對稱分布。每條支鏈包含一個驅動桿與一個從動臂，驅動桿一端通過驅動電機與定平臺相聯接，另一端以轉動副形式與從動臂相連，從動臂為平行四邊形結構，確保動平臺在工作空間內做三維平動。因為構件的柔性以及運動過程中慣性力和外載荷的影響，動平臺中心點P的實際位置相對于理想位置產生偏差，即彈性位置誤差，通過建立Delta機器人的彈性動力學方程可以對其彈性位置誤差進行計算。

1.1 單元劃分及位移分析

根據有限元理論，筆者選擇矩形截面梁單元作為基本單元，用以劃分機構中的柔性桿件，空間梁單元模型如圖2所示。

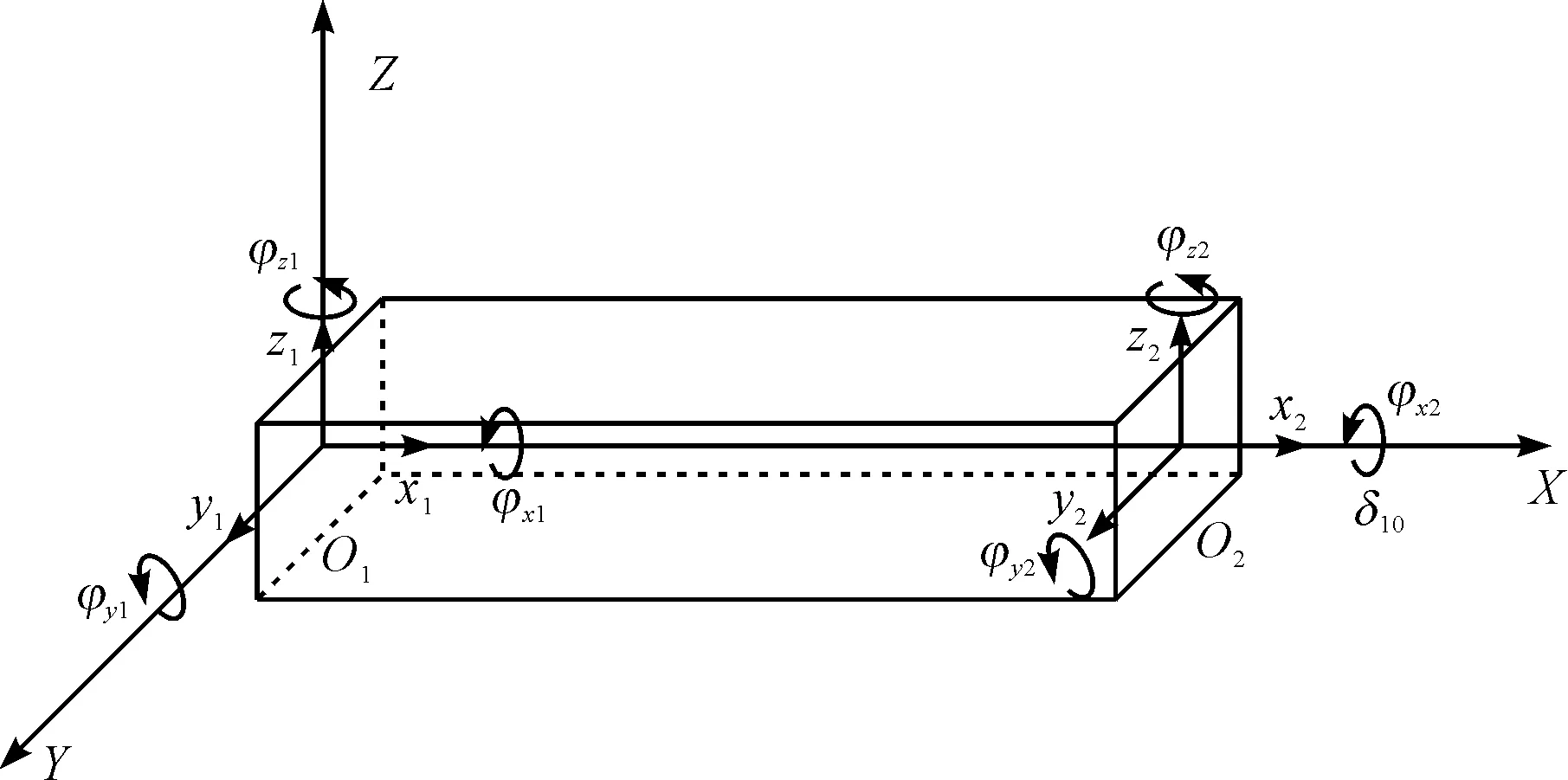
圖2 空間梁單元模型

單元包含2個節點。每個節點有6個彈性位移自由度，表示梁單元彈性位移的廣義坐標：

(1)

式中：x1，x2—兩節點在x軸向的彈性位移；y1，y2—兩節點沿y向彈性位移；z1，z2—兩節點沿z向彈性位移；φx1，φx2—兩節點繞x軸彈性轉角；φy1，φy2—兩節點繞y軸彈性轉角；φz1，φz2—兩節點繞z軸彈性轉角。

根據歐拉-伯努利梁理論，梁單元上任意一點彈性位移可以表示成如下形式：

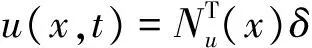
(2)

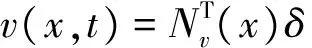
(3)

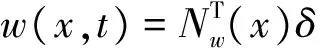
(4)

(5)

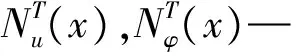
1.2 單元彈性動力學方程

因為單元彈性變形較小，忽略機構剛體運動與彈性變形運動之間的耦合影響，單元的位移看作是剛體位移與彈性位移的疊加，單元動能為：

(6)

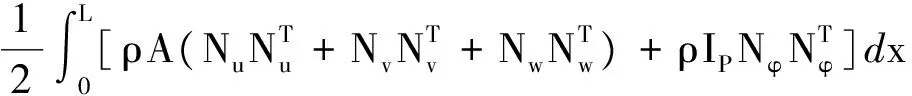
(7)

式中：ρ—單元質量密度；L—梁單元長度；A—梁單元截面面積；IP—梁單元橫截面對x軸的極慣性矩。

單元的變形能包括彎矩、軸向力和扭矩作用時所產生的能量，單元總變形能為：

(8)

式中：Ke—單元剛度矩陣。

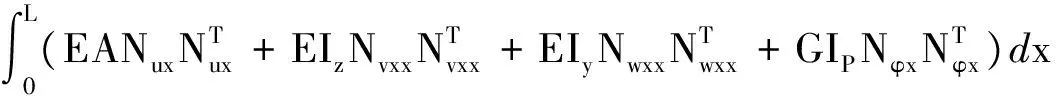
(9)

式中：E—梁單元材料的楊氏模量；G—梁單元材料的剪切模量；Iy，Iz—梁單元橫截面對y軸和z軸的極慣性矩，形函數下標中的x以及xx分別代表對x的一階偏導和二階偏導，例如：Nux代表Nu對x的一階偏導。

將式(6，8)代入拉格朗日動力學方程，導出單元彈性動力學方程：

(10)

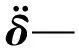
Fe=Qe+Pe+Ge

(11)

1.3 運動協調關系

1.3.1 支鏈內坐標系建立

鑒于Delta機器人支鏈的對稱性，本研究選取一條支鏈進行彈性動力學建模。支鏈有限元模型如圖3所示。

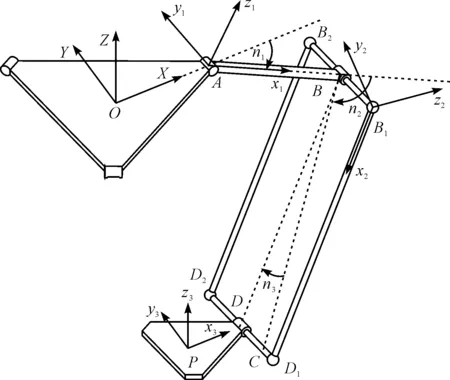
圖3 支鏈有限元模型

圖3中，A為驅動端，驅動桿AB被視為空間懸臂梁，B1B2D2D1為支鏈的平行四邊形從動臂結構，P為機器人末端，因為平臺剛度遠大于空間梁單元機構，視動平臺與定平臺為剛性體。而在四邊形機構中，上下短桿長度遠小于兩側桿，因此本研究將B1B2、D1D2兩桿視作剛性體，并忽略其質量影響，將B1D1、B2D2兩桿作為彈性桿件進行分析。

本研究在圖3中做驅動桿AB直線在B1B2D2D1平面上的投影BC，并如圖中定義角度n1、n2、n3。建立支鏈O-XYZ坐標系，方向定義為Z軸向上，Y軸平行于驅動器轉動軸線，X軸遵守右手定則指向支鏈方向；動平臺坐標系P-x3y3z3方向與支鏈坐標系O-XYZ一致；驅動桿AB單元坐標系A-x1y1z1的坐標軸方向由支鏈坐標系O-XYZ繞Y軸旋轉n1得到；從動桿B1D1單元坐標系B1-x2y2z2方向由支鏈坐標系O-XYZ先繞Y軸旋轉n1+n2，后繞Z軸旋轉n3得到。

定義支鏈彈性位移廣義坐標為：

(12)

其中，前6項元素組成P點在坐標系P-x3y3z3下廣義坐標UP，描述動平臺因為機構彈性變形影響，P點相對于名義位置的位移；7～12項元素組成廣義坐標UB，對應AB梁單元坐標系A-x1y1z1下B節點處的彈性位移；φ1-8分別為B1D1、B2D2兩桿端點在各自單元坐標系下繞y軸與z軸方向的彈性轉角。

1.3.2 支鏈內運動協調關系

驅動桿AB為空間懸臂梁，點A處的彈性位移與轉角均為零，可以得出AB梁單元與支鏈彈性位移之間的關系為：

δAB=SABΨ

(13)

其中：

(14)

式中：I—單位矩陣；0—零矩陣；δAB—AB梁單元廣義坐標。

記D點在動平臺坐標系P-x3y3z3下廣義坐標為：

(15)

則D點與P點位移協調關系為[8]：

(16)

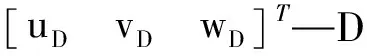
根據圖3中幾何約束關系可以得到B1D1梁單元在單元坐標系下的彈性位移：

x1=(xBc2+zBs2-d(φzBc2-φxBs2))c3+yBs3；

y1=-(xBc2+zBs2-d(φzBc2-φxBs2))s3+yBc3；

z1=zBc2-xBs2+d(φxBc2+φzBs2)；

φx1=0；φy1=φ1；φz1=φ2；

x2=(xDc12+zPs12-d(φzDc12-φxDs12))c3+yDs3；

y2=-(xDc12+zDs12-d(φzDc12-φxDs12))s3+yDc3；

z2=zDc12-xDs12+d(φxDc12+φzDs12)；

φx2=0；φy2=φ3；φz2=φ4

(17)

式中：d=1/2|B1B2|；符號s，c—函數sin和cos，下標數字對應3個角度n1、n2、n3，例如：s12代表sin(n1+n2)，c3代表cosn3。

由式(16，17)可以得出B1D1梁單元與支鏈彈性位移之間的協調關系：

δBD1=SBD1Ψ

(18)

式中：δBD1—B1D1梁單元廣義坐標；SBD1—B1D1梁坐標協調矩陣，同理可以得出B2D2梁單元與支鏈彈性位移之間的協調關系：

δBD2=SBD2Ψ

(19)

動平臺P與支鏈彈性位移協調關系為：

UP=SPΨ

(20)

式中：

1.3.3 系統運動協調關系

本研究建立系統廣義坐標U∈R48×1，根據式(13，18，19，20)，以及3條支鏈的對稱性，建立出任意構件i與系統廣義坐標U之間的協調關系：

δi=SiU

(21)

式中：i—構件編號；δi—構件i的單元廣義坐標；Si—對應的坐標協調矩陣。

1.4 系統彈性動力學方程

動平臺為剛體，其動力學方程[9-10]可以表示為：

(22)

其中，動平臺質量矩陣：

(23)

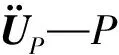
將式(19)代入式(10，22)得到各構件動力學方程：

(24)

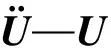
將各構件的單元動力學方程(24)進行總裝得到：

(25)

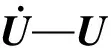
2 彈性誤差分析

2.1 彈性誤差計算

筆者選用系統參數：驅動桿長500 mm，動平臺質量0.2 kg，上平臺外接圓半徑100 mm，動平臺外接圓半徑為50 mm，從動臂結構中短桿長度為50 mm，兩側的從動桿長600 mm，驅動桿截面與從動桿截面均選用正方形截面，驅動桿截面邊長尺寸20 mm，從動桿截面邊長尺寸10 mm，材料密度為7 850 kg/m3，彈性模量210 GPa，泊松比0.3，運行時間T=3s。給定動平臺運動軌跡：

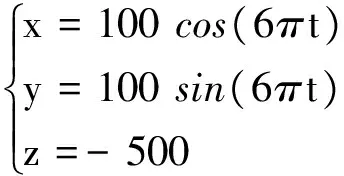
(26)

本研究利用Newmark方法在Matlab中對系統動力學方程(25)進行數值求解，計算出動平臺末端P點的彈性位置誤差在運行時間內的變化情況。

圓周軌跡下彈性位置誤差如圖4所示。

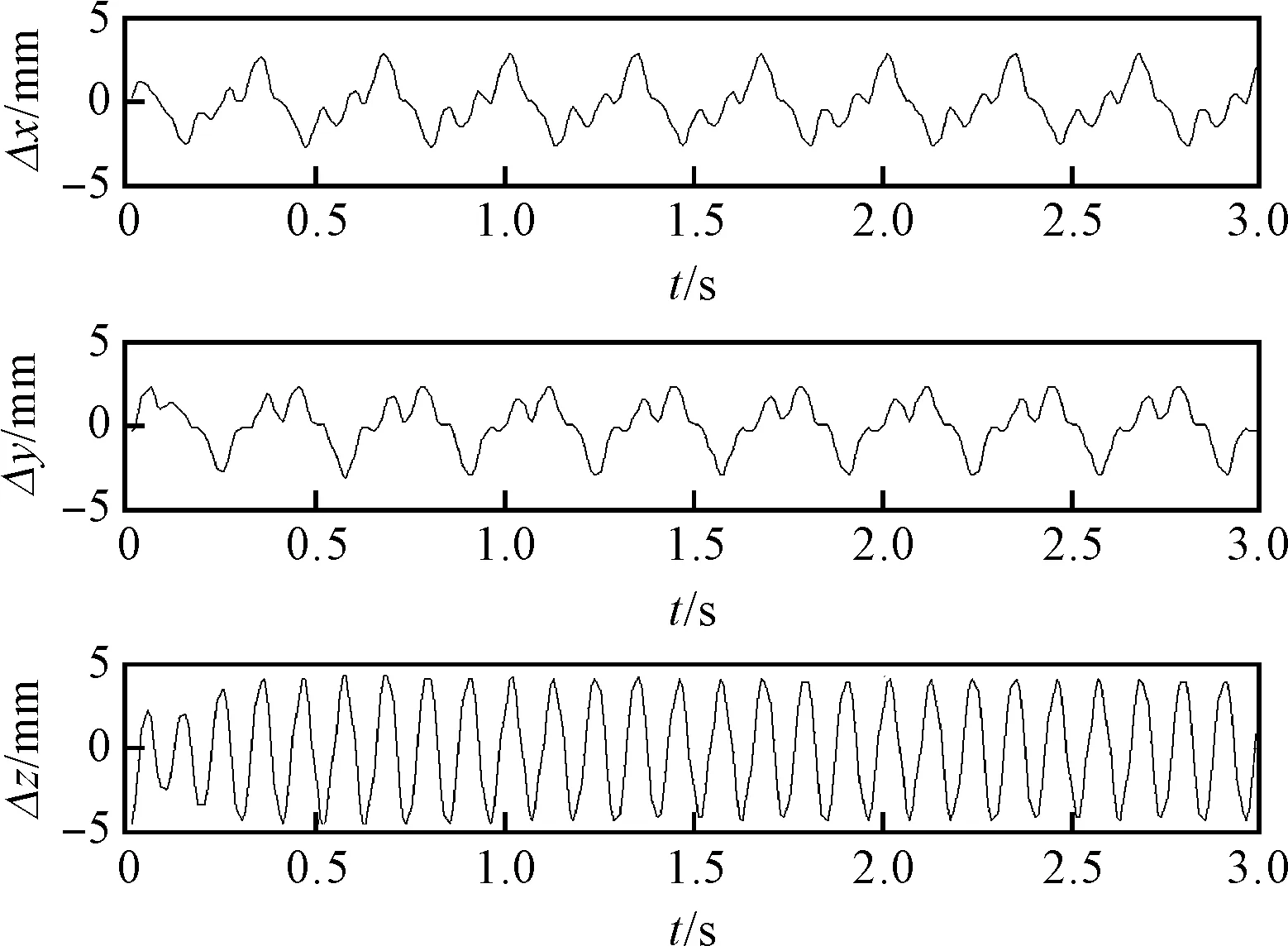
圖4 圓周軌跡下彈性位置誤差Δx、Δy、Δz—P點沿x、y、z三軸方向的彈性誤差。

2.2 桿截面尺寸對彈性誤差影響

通過改變驅動桿與從動桿的截面參數，可以有效改變機器人的力學性能。定義軌跡上誤差均值：

(27)

式中：Δx(t)，Δy(t)，Δz(t)—P點在t時刻沿各軸向的彈性誤差值。

2.2.1 驅動桿截面尺寸對彈性誤差影響

驅動桿截面邊長選擇取值20 mm～30 mm的范圍，其他參數不變。本研究根據式(27)計算誤差均值隨驅動桿的截面邊長的變化情況。結果如圖5所示。

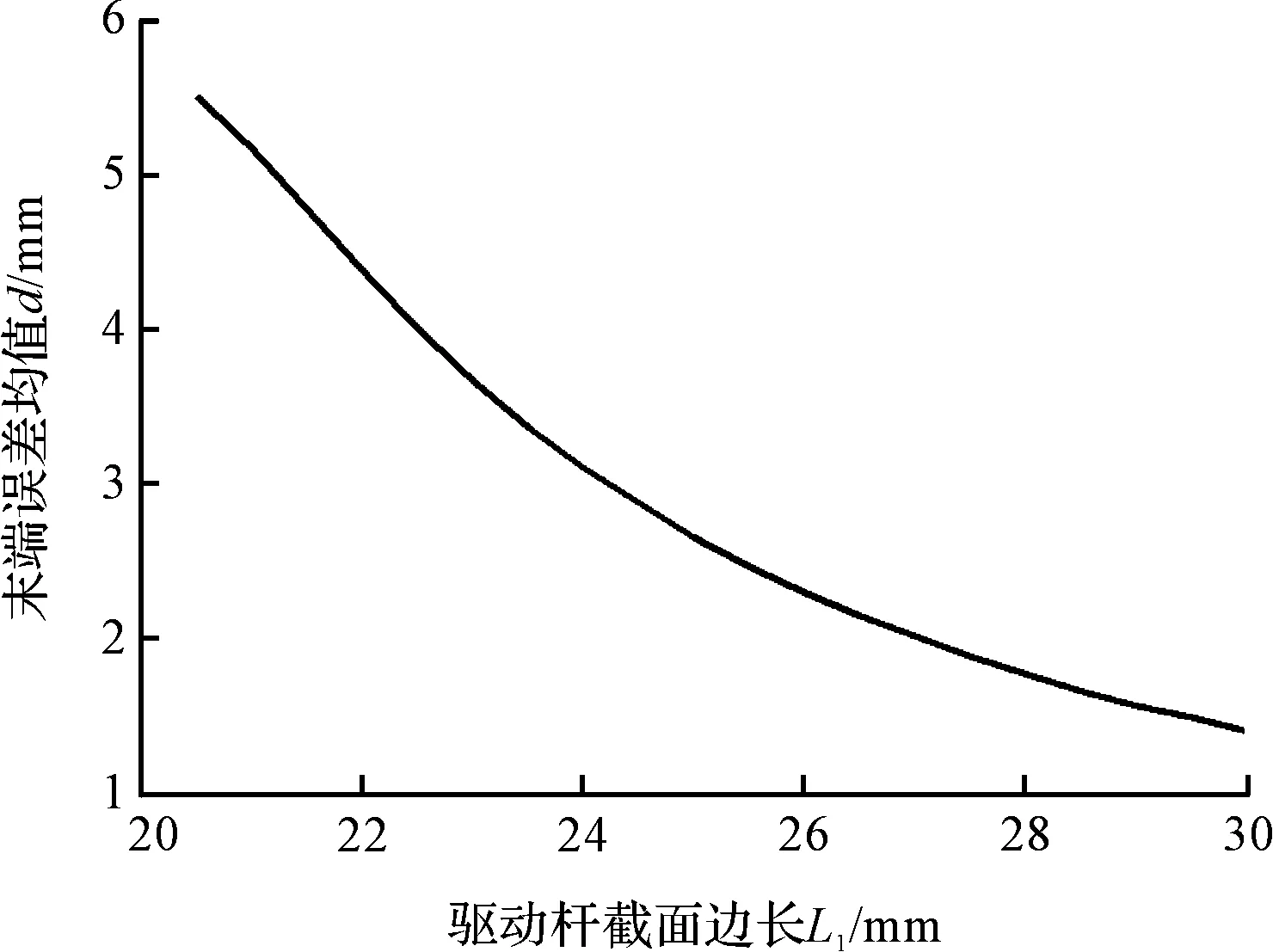
圖5 驅動桿截面尺寸對機構末端彈性誤差的影響

可以看到：隨著驅動桿截面邊長增大，機器人末端的誤差均值明顯減少。究其原因，驅動桿的受力形式類似于懸臂梁，增加其截面尺寸能夠有效提升其彎曲剛度。

2.2.2 從動桿截面尺寸對彈性誤差影響

考察從動桿截面尺寸對機構彈性誤差的影響，從動桿截面邊長選擇取值5 mm～10 mm的范圍，其他參數不變。誤差均值隨從動桿截面邊長的變化情況如圖6所示。

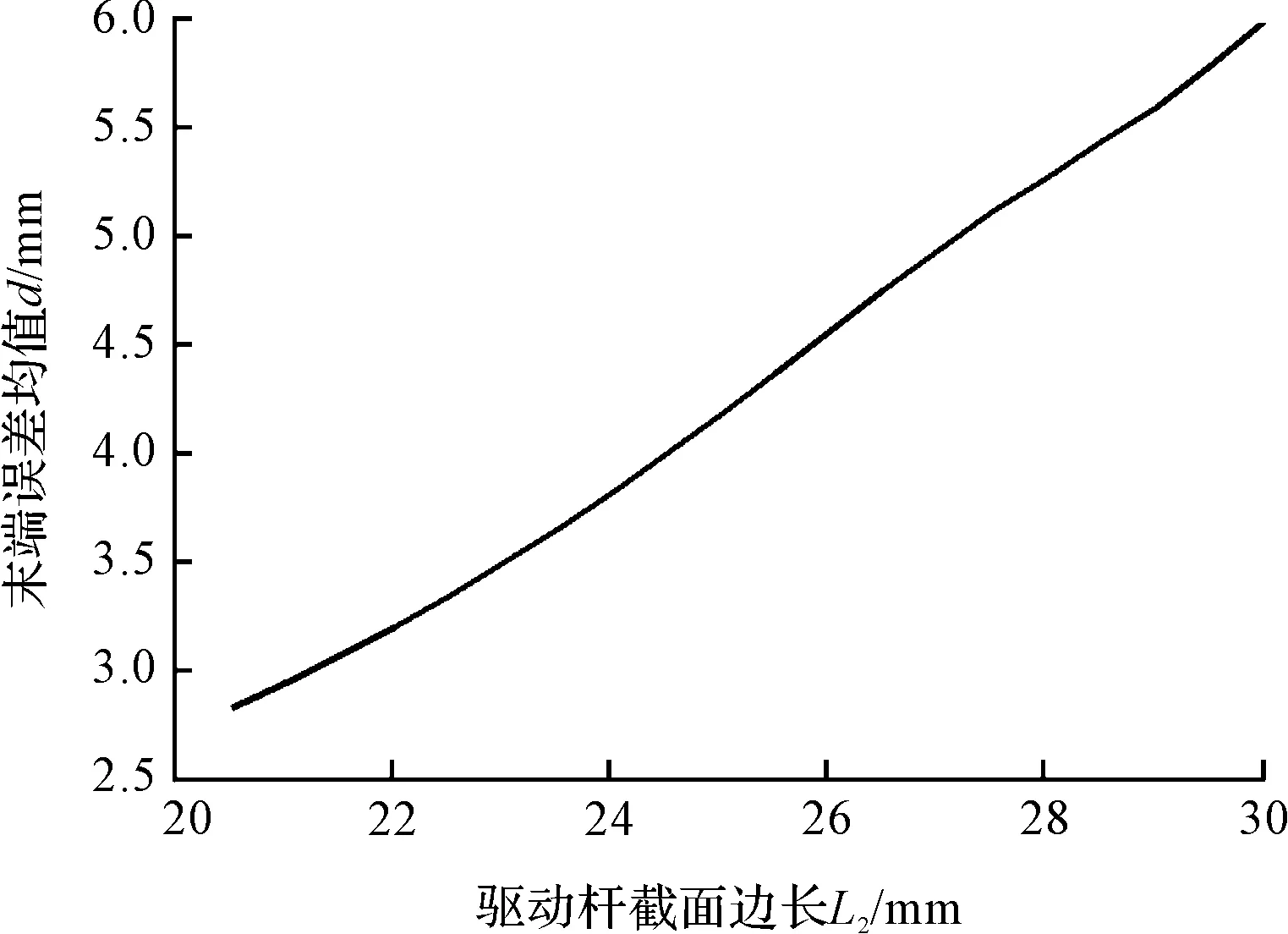
圖6 從動桿截面尺寸對機構末端彈性誤差的影響

由圖可以看到：當從動桿截面邊長增大時，機構的均值誤差隨之增加。分析原因，從動桿兩端均為球鉸關節，其變形方式以拉壓為主，相對于彎曲變形，軸向拉壓變形的尺寸相對較小，其剛度的提升并不能抵消掉由質量增加帶來的額外載荷影響。

2.2.3 兩桿截面尺寸對彈性誤差綜合影響

筆者考察兩種桿截面尺寸對機構彈性誤差的綜合影響，從動桿截面邊長選擇取值5 mm～10 mm的范圍，驅動桿截面邊長選擇取值20 mm～30 mm的范圍，其他參數不變，機器人均值誤差隨兩桿截面尺寸變化如圖7所示。

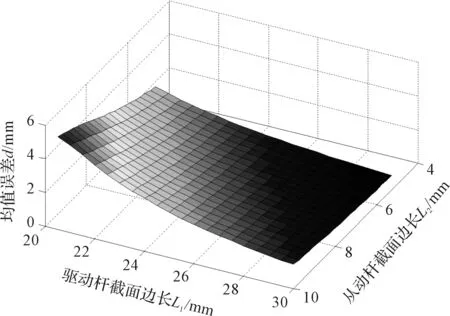
圖7 兩類桿截面尺寸對機構末端彈性誤差的綜合影響

可以看到在區間內均值誤差的變化規律，誤差均值與驅動桿截面尺寸呈負相關，與從動桿截面尺寸呈正相關，具有一定的單調性。

3 結束語

本研究針對Delta機器人運動過程中的彈性變形誤差進行了分析，建立了系統的彈性動力學控制方程，通過數值方法進行算例分析，求解出了機器人在運動過程中的誤差情況，分析了桿件截面尺寸對彈性誤差的影響。

結論顯示：通過增加驅動桿的截面尺寸以及減少從動臂的截面尺寸，能夠有效降低機器人運動過程中的彈性變形。

[1] CLAVEL R, A fast robot with parallel geometry[C]. Proc.Int.symposium. on Industrial Robots, Lausanne: CiNii,1988.

[2] 計時鳴,黃希歡.工業機器人技術的發展與應用綜述[J].機電工程,2015,32(1):1-13.

[3] 馮李航,張為公,龔宗洋,等.Delta系列并聯機器人研究進展與現狀[J].機器人,2014(3):375-384.

[4] PIRAS G, CLEGHORN W L, MILLS J K. Dynamic finite-element analysis of a planar high-speed, high-precision parallel manipulator with flexible links[J].Mechanism&MachineTheory,2005,40(7):849-862.

[5] 劉善增，朱真才,余躍慶,等.空間剛柔耦合并聯機構系統的頻率特性分析[J].機械工程學報,2011,47(23):39-48.

[6] 韓亞鋒,馬履中,吳偉光,等.Delta并聯機器人彈性動力學研究[J].農業機械學報,2011,42(10):197-202.

[7] KUO Y L. Mathematical modeling and analysis of the Delta robot with flexible links[J].Computers&MathematicswithApplications,2016,71(10):1973-1989.

[8] 黃 真,孔令富,方躍法.并聯機器人機構學理論及控制[M].北京：機械工業出版社,1997.

[9] 韓敬虎，俞經虎.食品檢測咀嚼機器人工作空間研究[J].輕工機械，2016，34(3)：1-4.

[10] 熊艷梅，楊延棟.碼垛機器人運動學分析與仿真[J].機械，2015(12)：62-66.

[11] 巴 特.有限元分析中的數值方法[M].北京:科學出版社,1985.