面向國產異構系統的HPL異構協同設計*

甘新標，孫燎原,劉 杰，雄成偉，黃嘉昆

(1.國防科技大學計算機學院,湖南 長沙 410073;2.計算機軟件新技術國家重點實驗室(南京大學)，江蘇 南京 210093;3.國防科技大學量子信息研究所兼高性能計算國家重點實驗室，湖南 長沙 410073)

1 引言

高性能計算是衡量國家科技能力的重要標志，已廣泛應用于大規模數值計算、武器裝備模擬仿真等領域。為了制衡和封鎖中國巨型機技術發展，美國商務部2015年2月18日發布芯片限售令，我國國家超級計算長沙中心、國家超級計算廣州中心、國家超級計算天津中心和國防科技大學4家機構被列入美國芯片限售對象。幸運的是，中國高性能處理器發展技術早有預案，國產加速器(China Accelerator)就是國防科技大學計算機學院自主研發的高性能加速器[1]。China Accelerator的軟件生態不同于GPU、MIC等比較成熟的加速器，其體系結構和編程模型更是有別于傳統的CPU體系結構和編程模式，開發高效的應用程序將面臨體系結構復雜、細節多，并行編程要求高、難度大，數據流動管理與分派繁瑣復雜，優化困難等諸多挑戰。因此，面向國產異構系統的HPL(High Performance Linpack)異構協同設計可以為China Accelerator廣泛應用于核爆模擬、天氣預報、地質資源勘查等領域提供技術參考，加速China Accelerator的推廣應用。

線性系統軟件包Linpack(Linear system package) 通過使用高斯消元法求解稠密一元N次線性代數方程組來評估高性能計算機的實際浮點性能,Linpack根據問題規模與優化選擇的不同分為Linpack100、Linpack1000 以及HPL[2]。HPL采用高斯消元法求解N元一次稠密線性代數方程組來評估高性能計算機的浮點性能。高斯消元法首先將系數矩陣A通過分塊遞歸的LU分解,將其分解為一個下三角陣L與一個上三角陣U的乘積,然后將線性代數方程組Ax=b演算成Ux=L-1b形式,最后,通過上三角方程回代求得線性方程組的解[3 - 5]。HPL由于規模可變,成為目前最流行的用于測試高性能計算機浮點性能的測試基準。當HPL求解問題規模為N時，浮點計算次數為(2/3)N3+(3/2)N2，計算時間為T，HPL測試浮點性能值為(2/3)N3+(3/2)N2)/T，浮點計算性能測試結果是高性能機Top500排名的重要依據。

由于支持China Accelerator的底層矩陣乘接口目前僅支持定制接口，為了提供一個通用的HPL測試環境，需要完成矩陣循環分布細致劃分與封裝dPEM(delicate Partition and Encapsulation on Matrix)。同時，為了充分發揮國產異構系統的效率，設計了異構協同矩陣乘調度算法OA4MM(Orchestrating Algorithm for Matrix Multiplication)。

2 面向CPU+China Accelerator的HPL設計

傳統HPL算法中，求解N×N矩陣將以塊為單位循環分布到所有CPU，由于矩陣采用了塊循環分布，在N較大時，各個處理器的計算量基本相當，對于同構系統，傳統的HPL一般可以獲得較高的系統性能。由于計算速度的差異，如果給異構系統中每個處理器分配相同的計算量，那么計算速度快的加速器在完成計算后必須等待計算速度較慢的CPU進行通信，必然降低異構系統效率。因此，為了充分發揮異構系統的效率，必須基于異構系統結構設計高效協同的HPL算法。由于矩陣乘更新操作占據了HPL求解絕大部分計算時間，因此高效協同的HPL算法設計將滿足CPU端矩陣乘更新計算時間TCPU與China Accelerator端矩陣乘更新計算時間TChina Accelerator在相同時間點完成各自的計算，避免不必要的通信等待。即:

其中，M、N、K分別為矩陣A(M,K)、B(K,N)、C(M,N)的緯度。

2.1 支持China Accelerator的矩陣乘定制接口封裝

China Accelerator由6個DSP超節點、1個CPU節點、1個IO節點、全局Cache、核間同步、4個存儲控制器MCU(Memory Control Unit)及IO設備構成。其中，每個DSP超節點包含兩個飛騰―Matrix2000內核，每個飛騰―Matrix2000內核包含兩個計算核心，每個計算核心包含16個向量計算功能單元；全局Cache GC(Global Cache)采用分布式Cache，由多個子體(SubGC)構成，每兩個SubGC連接一個存儲控制單元MCU；核間同步也采用分布式組織，由多個子體構成。上述節點、SubGC、MCU由環形互連連接。 因此，China Accelerator是一款面向計算密集型應用、能高效處理大量數據的高性能多向量體系結構加速器，如圖1所示[1]。

Figure 1 China Accelerator體系結構圖1 Architecture of China Accelerator

如圖1所示，China Accelerator體系結構復雜、細節多，數據分派繁瑣。為了最大化國產加速器計算資源利用率和提高處理器的性能，支持China Accelerator的底層矩陣乘接口目前僅支持定制接口，即，支持國產加速器China Accelerator的矩陣乘接口僅支持特定規模的矩陣乘A(FT_m,K)×B(K,N)，FT_m是FT-Matrix支持的矩陣乘中第一矩陣的行數，K是FT-Matrix支持的矩陣乘中第一矩陣的列數，也是第二矩陣的行數，N是FT-Matrix支持的矩陣乘中第二矩陣的列數，A(FT_m,K)×B(K,N)中對N、K沒有特殊限制，但是，FT_m只能是576的整數倍，并且必須大于或等于576×6。然而，支持通用CPU的基本線性代數庫矩陣乘接口是能支持任意規模的矩陣乘A(L,K)×B(K,N)，即A(L,K)×B(K,N)中的L、K、N為任意的正整數。

因此，傳統的HPL矩陣乘調度方法不再適合于面向China Accelerator的HPL矩陣乘調度優化，國產China Accelerator迫切需要一種適用于定制接口的異構矩陣乘調度優化方法，將國產加速器僅支持定制接口的異構矩陣乘封裝為類似CPU支持的通用矩陣乘，并且，最大化矩陣塊循環分布計算效率，提升國產異構系統效率。CPU + China Accelerator異構系統的高效協同矩陣乘計算更新劃分如圖2所示。

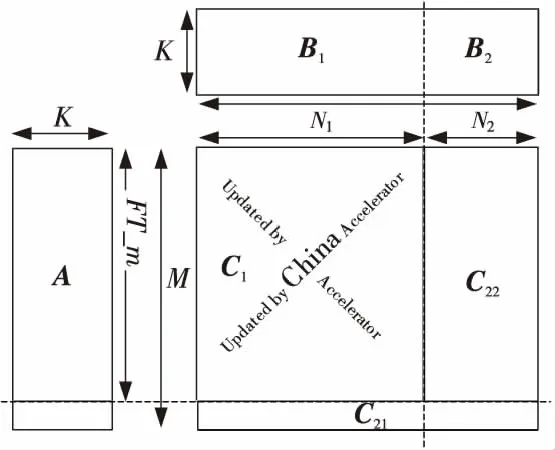
Figure 2 Matrix multiplication between CPU and China Accelerator with coordination圖2 協同矩陣乘更新

如圖2所示，由于China Accelerator目前支持的矩陣乘接口為定制接口，高效協同的矩陣乘更新算法中，CPU不僅要負責邊緣非規則的矩陣乘計算，還必須與China Accelerator協同完成規則的矩陣乘更新操作。

2.2 異構協同矩陣乘調度算法

面向異構系統的矩陣乘調度可分為靜態劃分調度SdS(Static dispatch Strategy)和動態調度dSd(dynamic Schedule dispatch)。面向CPU+GPU的天河1A異構系統中，矩陣乘調度以靜態調度為主，即，探索最優GPU端矩陣乘劃分比例，如公式(2)所示。

其中，Gaccelerator為加速器GPU端矩陣乘更新時間，GCPU為CPU端矩陣乘更新時間。

在天河1A異構系統中，GPU端負責計算更新的矩陣子塊大小預先已經確定[6,7]，通過將CPU與GPU之間的數據傳輸時間隱藏于計算過程中來優化提升異構系統效率；與天河1A異構系統不同，面向CPU+MIC的天河二號異構系統中，矩陣乘調度算法以基于隊列緩沖的動態調度為主[8,9]，即，當前矩陣乘更新操作是分派至CPU還是MIC取決于任務計算隊列的狀態，以最大限度實現異構系統均衡，提高異構系統效率。

面向CPU+China Accelerator的HPL異構設計中，若采用類似天河1A的靜態劃分策略SdS，由于面向China Accelerator的底層數學庫矩陣乘接口限制，只有滿足接口規范要求的矩陣乘計算才能夠調度到China Accelerator上加速，大部分的矩陣乘計算只能在CPU端完成更新操作；若采用基于隊列緩沖的天河二號異構系統HPL矩陣乘更新動態調度方法dSd，將產生冗余的隊列狀態查詢和計算任務請求等待。這是因為部分矩陣乘接口明顯不符合China Accelerator內置的定制接口，但是，仍然需要監控隊列狀態并試圖發送計算任務請求。

不同于天河1A異構系統中矩陣乘調度靜態劃分策略和天河二號異構系統中基于隊列緩沖的矩陣乘更新動態調度方法，基于China Accelerator體系結構和軟件生態，設計了一種異構協同矩陣乘調度算法OA4MM,以提高國產異構系統的效率。OA4MM調度方法屬于一種基于天河1A和天河二號的動靜融合協同矩陣乘均衡調度算法，OA4MM在矩陣乘靜態劃分的基礎上引入動態調度策略，最小化動態調度中冗余的隊列狀態查詢和計算任務請求等待，同時，最大限度劃分矩陣乘更新調度至China Accelerator端加速，算法流程如圖3所示。

Figure 3 OA4MM調度算法流程圖3 Flow chart of OA4MM

3 實驗結果與分析

3.1 CPU+China Accelerator驗證系統

針對CPU+China Accelerator驗證系統結構，系統設計的基于China Accelerator的計算刀片，靈活支持增添基于China Accelerator的加速子板，滿足計算刀片能靈活可配、按需構建的用戶需求。加速子板(包含4個China Accelerator)通過PCIE與計算刀片相連，并通過計算刀片上的高速網卡NIO(Network Input and Output)接入高速互連網絡，實現計算結點間的互連。

CPU+China Accelerator驗證系統由16個計算結點組成，如圖4所示。單結點主要配置如表1所示。

3.2 矩陣分塊對性能影響

由于China Accelerator目前僅支持特定規模的矩陣乘A(FT_m,K)×B(K,N)，國產加速器底層支持的矩陣乘接口規范中對N、K沒有特殊限制，但是，FT_m只能是576的整數倍，并且必須大于或等于576×6，為了充分利用China Accelerator強大的計算資源，調度至國產加速器上進行加速計算的矩陣塊大小必然影響國產加速器的計算資源利用率和PCIE帶寬的占有率，因此，矩陣分塊大小將嚴重影響面向CPU+China Accelerator異構系統的HPL性能，其詳細測試結果如圖5所示。

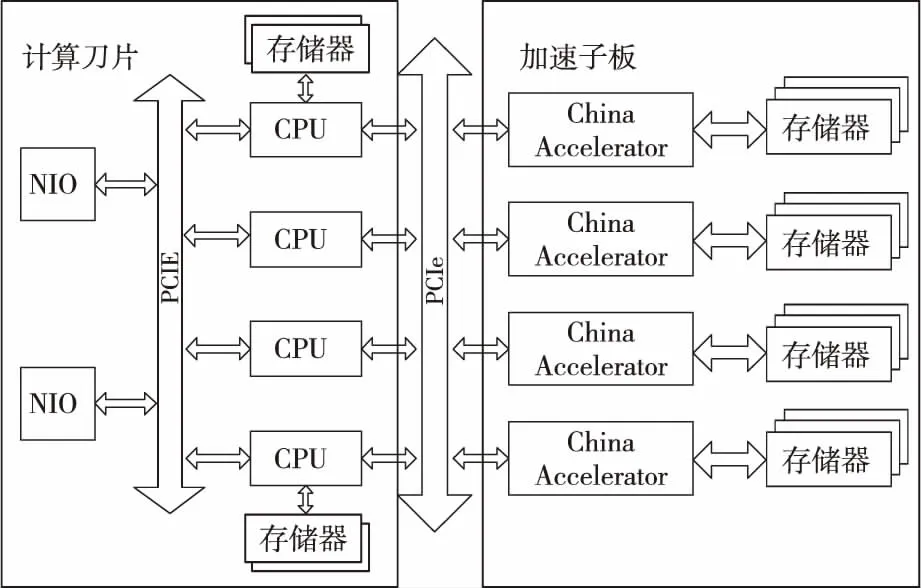
Figure 4 Architecture of node in experimental systems equipped with CPU and China Accelerator圖4 CPU+China Accelerator單結點驗證系統

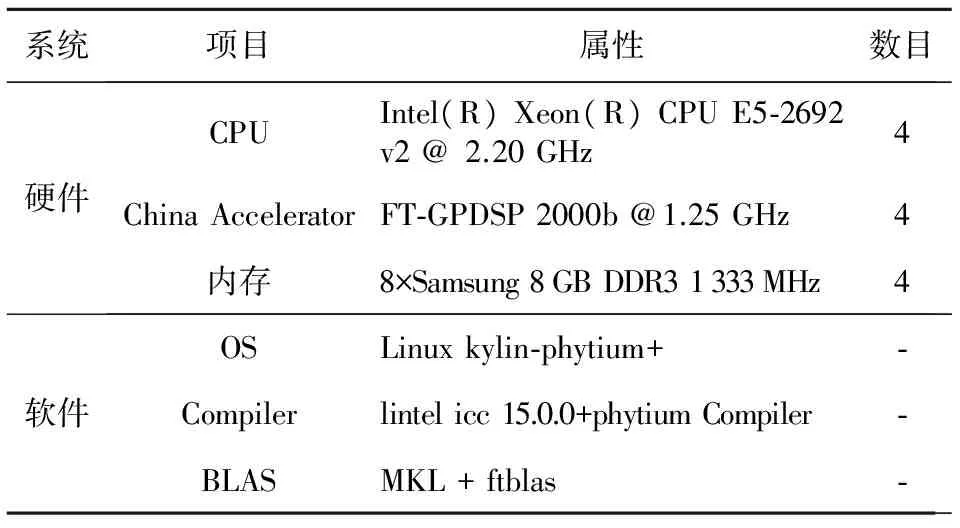
系統項目屬性數目硬件CPUIntel(R)Xeon(R)CPUE5?2692v2@2．20GHz4ChinaAcceleratorFT?GPDSP2000b@1．25GHz4內存8×Samsung8GBDDR31333MHz4軟件OSLinuxkylin?phytium+?Compilerlintelicc15．0．0+phytiumCompiler?BLASMKL+ftblas?

Figure 5 Performance evaluation on matrix block圖5 矩陣分塊的性能影響

以576×6的程序性能為基準，不同矩陣分塊大小的加速比如圖5所示。隨著矩陣分塊逐漸增大，程序性能顯著上升至拐點后開始平穩回落，這是因為當矩陣分塊較小時，頻繁的數據傳輸嚴重影響程序性能，當程序性能達到局部最高點后，加速器端的存儲資源就成為制約程序性能的關鍵。

3.3 OA4MM算法驗證

為了充分驗證OA4MM算法的高效性，面向CPU+China Accelerator的HPL設計配置了類似天河1A的靜態劃分策略SdS、基于隊列緩沖的天河二號的動態調度方法dSd以及高效協同矩陣乘調度算法OA4MM，以探索CPU+China Accelerator異構系統的效率，上述三種異構調度方法的實測性能比較如圖6所示，其中OA4MM的算法性能是在FT_m=576×30 時,即，最佳矩陣分塊情況下的測試性能。

Figure 6 Performance evaluation with OA4MM and SdS/dSd圖6 OA4MM與SdS/dSd的性能評估

由圖6可知，高效協同矩陣乘調度算法OA4MM較天河1A異構系統中的靜態劃分策略SdS性能提升幅度隨著計算結點數目和矩陣規模的增加逐漸明顯；同時，在CPU+China Accelerator異構系統中，隨著計算結點數目和矩陣規模的增加，OA4MM性能較天河1A的靜態劃分策略SdS和天河二號的動態調度方法dSd均有明顯提升，全系統HPL性能提升近10%。

4 結束語

鑒于HPL參數配置優化實驗在諸多文獻中已有詳細研究，面向國產異構系統的HPL異構協同設計將遵循China Accelerator矩陣乘接口規范，提出了dPEM方法對China Accelerator支持的底層數學庫定制接口進行封裝，屏蔽了定制接口限制，提供一個友好的HPL測試環境。為了最大限度發揮國產加速器的性能,提出了OA4MM調度算法。實驗結果驗證了dPEM的有效性和OA4MM算法的高效性,全系統HPL測試性能較傳統的異構矩陣乘調度方法提升近10%，提高了基于國產加速器的異構系統效率，未來的工作將對OA4MM算法進行形式化描述和論證，并嘗試將OA4MM調度算法應用至由GPU、MIC構建的異構實驗系統中。

[1] Lu Yu-tong. Applications leveraging supercomputing systems[R].ISC’2015,2015.

[2] Dongarra J J, Luszczek P,Petitet A.The linpack benchmark: Past,present,and future[J].Concurrency and Computation: Practice and Experience,2003,15(9): 803-820.

[3] Zhang Wen-li, Chen Ming-yu,Fan Jian-ping.Emulation and forecast of HPL test performance [J]. Journal of Computer Research and Development,2006,43(3):557-562.(in Chinese)

[4] Liu Gang, Zhang Heng,Zhang Dian,et al.Optimization of Linpack for Loongson 3B processor [J]. Journal of Shenzhen University (Science & Engineering),2014,31(3):286-292.(in Chinese)

[5] Liu Jie,Hu Qing-feng,Chi Li-hua,et al.Parallel performance analysis of high performance Linpack[C]∥Proc of 2004 National Conference on High Performance Computing,2004:1.(in Chinese)

[6] Yang Xue-jun, Liao Xiang-ke,Lu Kai,et al.The TianHe-1A supercomputer: Its hardware and software[J].Journal of Computer Science and Technology,2011,26(3): 344-351.

[7] Wang Q, Ohmura J, Shan A, et al.Parallel matrix-matrix multiplication based on HPL with a GPU-accelerated PC cluster[C]∥Proc of the 1st International Conference on Networking and Computing, 2010:243-248.

[8] Du Yun-fei,Yang Can-qun,Wang Feng,et al.Analysis and evaluation method for Linpack benchmark [J].Dongbei Daxue Xuebao/Journal of Northeastern University,2014,35: 102-107.

[9] Liu Fang-fang,Yang Chao,Liu Yi-qun,et al.Reducing communication overhead in the high performance conjugate gradient benchmark on Tianhe-2[C]∥Proc of the 13th International Symposium on Distributed Computing and Applications to Business,Engineering and Science,2014:13-18.

附中文參考文獻:

[3] 張文力，陳明宇，樊建平,等.HPL測試性能仿真與預測[J].計算機研究與發展，2006，43(3)：557-562.

[4] 劉剛,張恒,張滇，等.基于龍芯3B 處理器的Linpack 優化實現[J].深圳大學學報(理工版)，2014，31(3):286-292.

[5] 劉杰，胡慶豐，遲利華，等.高性能Linpack并行計算性能分析[C]∥全國高性能計算學術會議，2004:1.