基于干擾力矩辨識的高精度非線性姿態(tài)控制方法

王 勇，張 艷，薛 輝，李延軍，檀朋碩

?

基于干擾力矩辨識的高精度非線性姿態(tài)控制方法

王 勇，張 艷，薛 輝，李延軍，檀朋碩

（北京宇航系統(tǒng)工程研究所，北京，100076）

彈道式航天飛行器末修閉路制導飛行段通常采用具有非線性特性的固定姿控噴管進行姿態(tài)跟蹤和穩(wěn)定控制，此時姿態(tài)控制精度直接影響閉路制導效果。傳統(tǒng)斜線開關線控制方法存在系統(tǒng)性姿態(tài)角偏差，導致末修推力方向與待增速度方向始終存在差異，進而影響到飛行器落點精度。提出的基于干擾力矩辨識的高精度非線性姿態(tài)控制方法，通過干擾力矩在線辨識，實時設計姿控噴管開關線，將極限環(huán)調整至環(huán)繞原點，從而提高姿控精度。基于某型飛行器的仿真結果表明，與傳統(tǒng)設計方法相比，基于干擾力矩辨識的高精度非線性姿態(tài)控制方法可將閉路制導段姿態(tài)控制精度提高約90%，減小姿態(tài)偏差對閉路制導的影響，飛行器落點精度提高約25%。

干擾力矩辨識；高精度；非線性；極限環(huán)

0 引 言

彈道式航天飛行器主動段飛行結束后，為提高落點精度，往往設計末速修正飛行段，通過閉路制導方法修正飛行器速度。其中，末速修正往往采用固定安裝的正推噴管[1]。末速修正過程中，通過姿態(tài)控制系統(tǒng)使正推噴管推力方向處于閉路制導給出的待增速度方向，此時，姿態(tài)控制精度直接影響到推力方向與待增速度方向的一致性，進而影響到飛行器落點精度。彈道式飛行器往往采用姿控噴管，通過電磁閥實現(xiàn)斷續(xù)姿態(tài)控制[2]，此時系統(tǒng)存在非線性特性。姿控噴管常采用經(jīng)典的斜線開關線設計非線性控制律[3]，在存在干擾力矩的情況下，始終存在系統(tǒng)性姿態(tài)角偏差，影響到末修閉路制導效果，使飛行器落點精度變差。

本文針對末修閉路制導飛行段非線性姿態(tài)控制設計問題，提出了基于干擾力矩辨識的高精度非線性姿態(tài)控制方法。首先，分析了姿態(tài)控制精度對末修閉路制導的重要性，介紹了傳統(tǒng)斜線開關線控制方法，推導了斜線開關線極限環(huán)模型，提出了一種干擾力矩在線辨識方案，并基于該方案提出了極限環(huán)環(huán)繞原點的開關線設計方法。針對某型飛行器開展了仿真，結果表明，與傳統(tǒng)設計方法相比，本文提出的方法可有效改善末修閉路制導飛行段姿態(tài)控制精度，減小姿態(tài)偏差對閉路制導的影響，提高飛行器落點精度。

1 姿態(tài)控制精度對飛行器閉路制導的影響

2 傳統(tǒng)斜線開關線控制方法

姿控噴管非線性特性包括過零的非線性特性和不過零的非線性特性[14]。兩種非線性特性及設計方法均無本質區(qū)別，不失一般性，本文針對具有過零非線性特性的姿控噴管開展研究。傳統(tǒng)姿控噴管采用經(jīng)典的比例-微分控制律，即在姿態(tài)角-姿態(tài)角速度相平面上，噴管開關線設計為斜線。在不考慮延遲情況下：

噴管正向理論開關線為

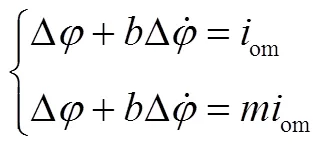
負向理論開關線為

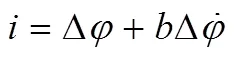
采用傳統(tǒng)的斜線開關線控制的穩(wěn)態(tài)結果無法到達原點，而是收斂于一個固定極限環(huán)。假定某型飛行器三通道已實現(xiàn)解耦控制，以俯仰單通道為例，無干擾力矩情況下，系統(tǒng)相軌跡如圖1所示。由圖1可以看出，系統(tǒng)相點軌跡為穩(wěn)定的環(huán)繞原點的閉合曲線，即極限環(huán)，其大小與電磁閥的開關門限和磁滯特性有關。

實際上，彈道式飛行器末速修正飛行段會受到干擾力矩作用，包括常值干擾和隨機干擾。在干擾力矩作用下，系統(tǒng)相軌跡如圖2所示。當系統(tǒng)相點趨于穩(wěn)定時，存在固定姿態(tài)角偏差。在圖2所示的極限環(huán)情況下，飛行器閉路制導過程中，飛行器姿態(tài)角與閉路制導給出的姿態(tài)角程序角之間始終存在一定的差異，導致推力方向與待增速度方向始終存在一定差異，從而影響閉路制導末速修正效果，進而影響落點精度。從閉路制導需求而言，極限環(huán)越小，極限環(huán)中心越靠近原點，推力方向與待增速度方向最接近，則對閉路制導效果影響越小。

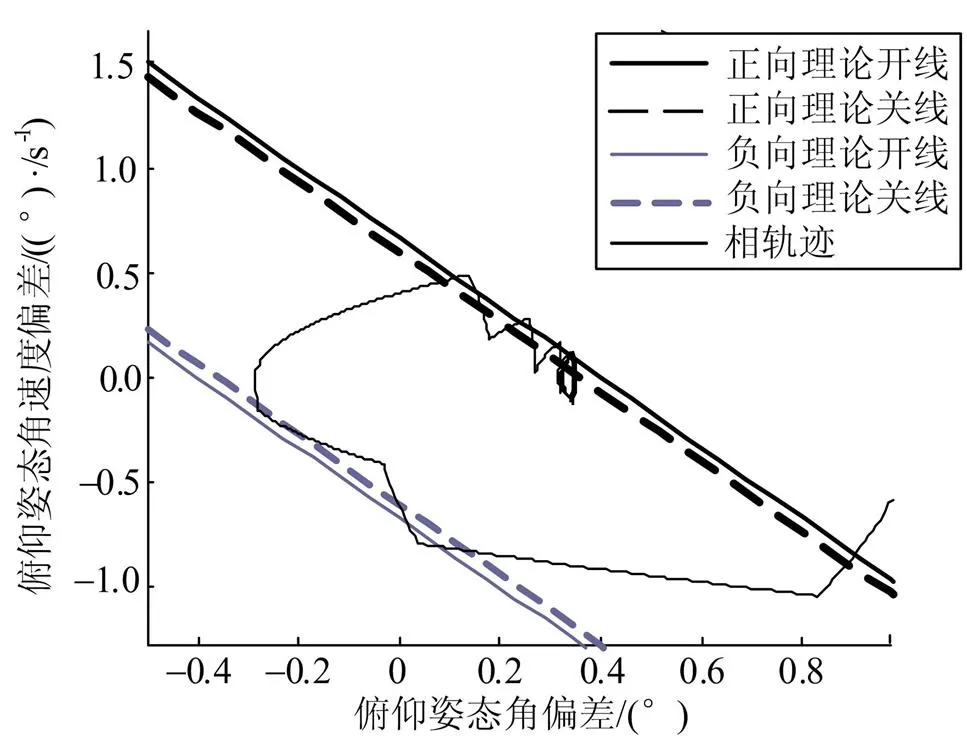
圖1 無干擾力矩時斜線開關線控制極限環(huán)情況

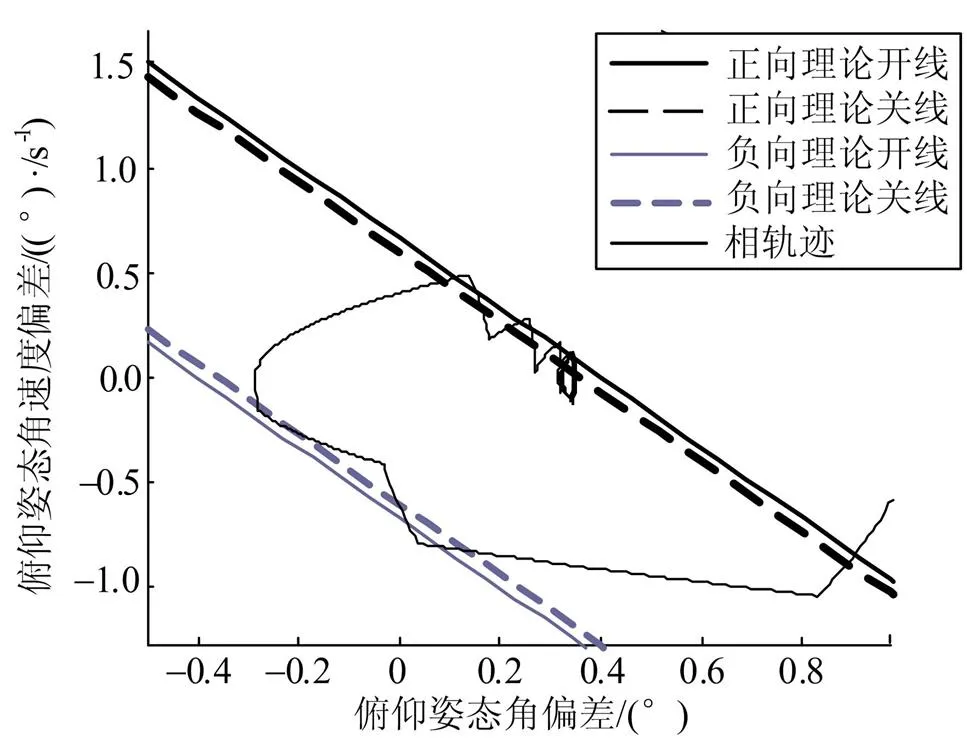
圖2 有干擾力矩時斜線開關線控制極限環(huán)情況

3 基于干擾力矩辨識的高精度非線性姿態(tài)控制方法

傳統(tǒng)開關線設計時，僅依據(jù)姿態(tài)控制精度需求進行開關門限和微分環(huán)節(jié)參數(shù)設計，未考慮存在干擾力矩情況下系統(tǒng)極限環(huán)情況，以及系統(tǒng)極限環(huán)對閉路制導過程的影響。本文提出基于干擾力矩辨識的高精度非線性姿態(tài)控制方法，在系統(tǒng)開關線設計時綜合考慮極限環(huán)位置，降低姿態(tài)控制偏差對末修閉路制導的影響。

3.1 斜線開關線極限環(huán)模型

考慮延遲情況，開關線控制的理論極限環(huán)如圖3所示。

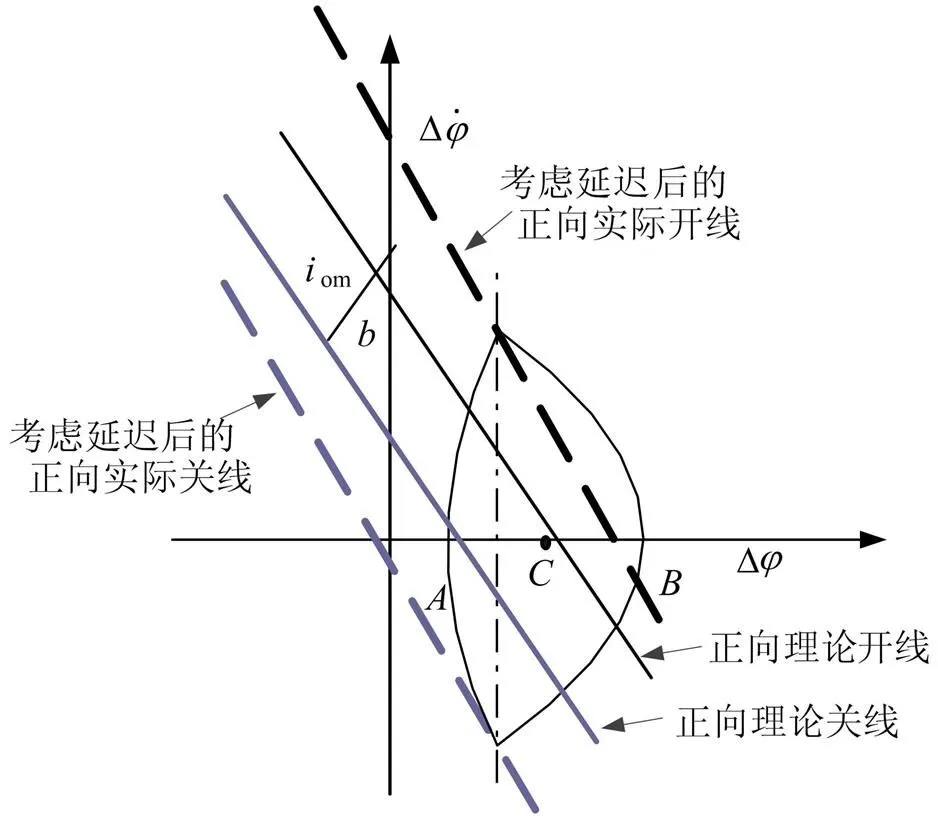
圖3 開關線控制理論極限環(huán)

點—極限環(huán)與橫軸的左側交點，其坐標為；點—極限環(huán)與橫軸的右側交點，其坐標為；點—極限環(huán)中心，其坐標為

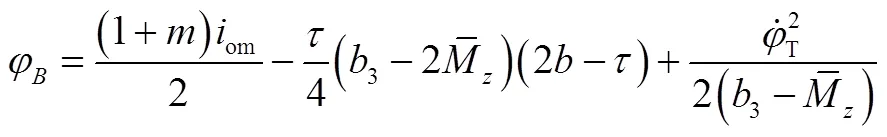
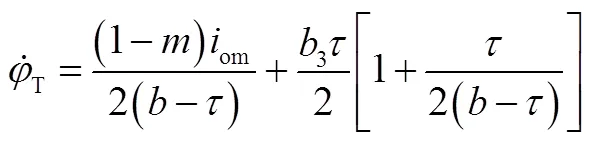
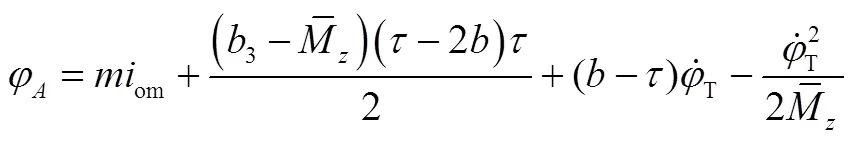
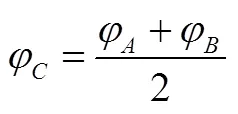
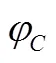
3.2 飛行器干擾力矩在線辨識模型

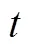
3.3 極限環(huán)環(huán)繞原點的開關線設計方法

在線辨識得到飛行器干擾力矩系數(shù)后，此時式（5）至式（8）中所有量均為已知量。為降低姿態(tài)偏差對末修閉路制導的影響，在控制律設計時，開關線可按使系統(tǒng)穩(wěn)態(tài)情況下的極限環(huán)環(huán)繞原點進行設計。根據(jù)干擾力矩情況下系統(tǒng)相軌跡運行規(guī)律，在干擾力矩系數(shù)已知時，通過將傳統(tǒng)開關線進行平移，可以調整穩(wěn)態(tài)情況下系統(tǒng)穩(wěn)定極限環(huán)。平移量可依據(jù)有干擾力矩情況下極限環(huán)原點位置進行確定。此時，噴管正向理論開關線設計為

噴管負向理論開關線設計為

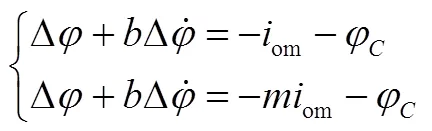
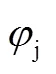
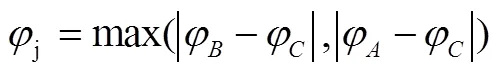
將該設計方法應用于某型飛行器，則俯仰通道極限環(huán)情況如圖4所示。

圖4 極限環(huán)環(huán)繞原點的斜線開關控制相軌跡

4 仿真分析

以某型飛行器為例，分別采用傳統(tǒng)開關線設計方法和本文提出的高精度非線性姿態(tài)控制方法開展三通道控制律設計，并基于兩種控制律開展了典型工況下的六自由度仿真。

采用傳統(tǒng)開關設計方法時，飛行器落點縱向偏差為0.59 m，橫向偏差為0.16 m。圖5、圖6給出了末修過程中俯仰和偏航姿態(tài)角跟蹤程序角情況。

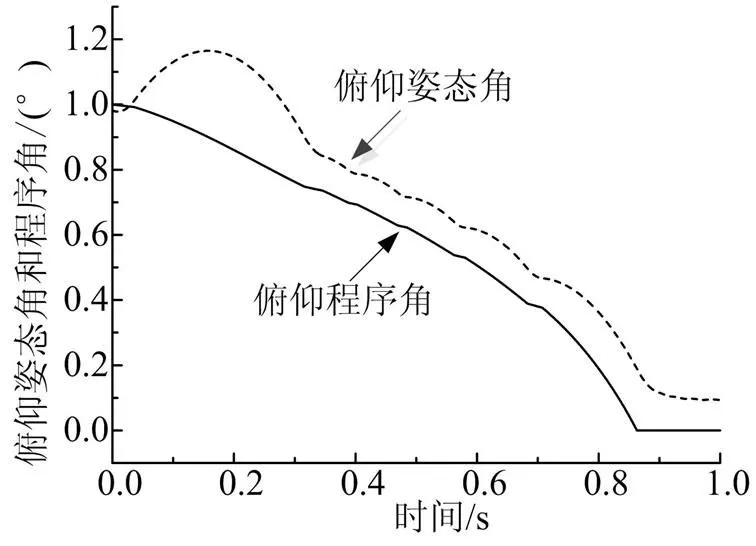
圖5 末修過程中俯仰角和俯仰程序角

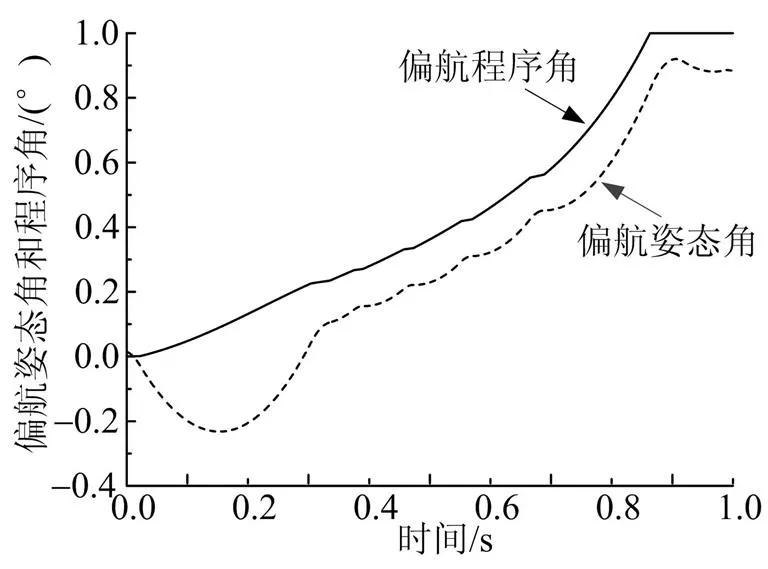
圖6 末修過程中偏航角和偏航程序角

圖7、圖8給出了末修過程中俯仰和偏航通道姿態(tài)相軌跡運行情況。由圖中曲線可以看出，姿態(tài)角與姿態(tài)程序角間存在系統(tǒng)性偏差。

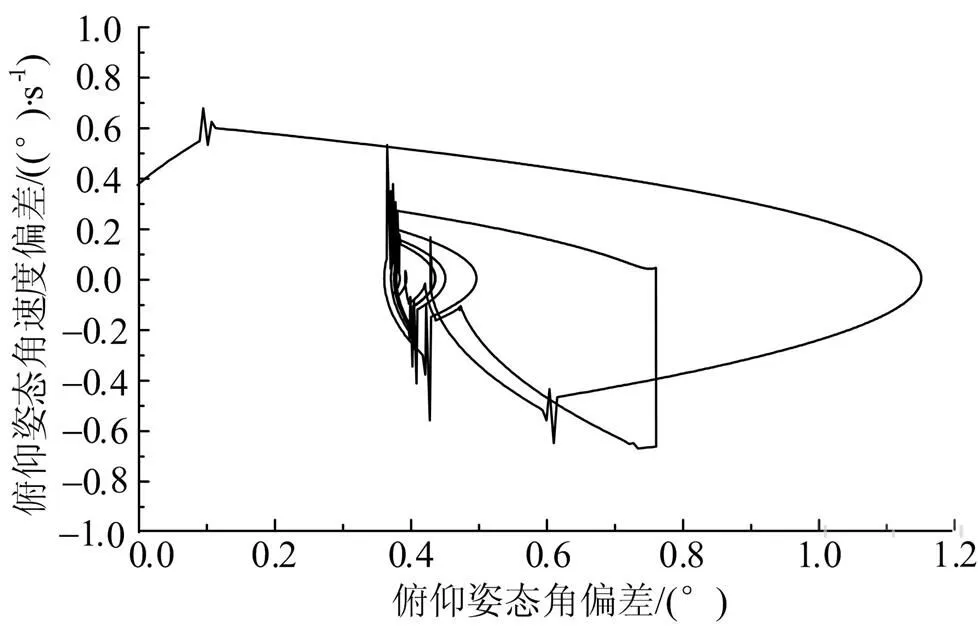
圖7 俯仰通道相軌跡運行情況

圖8 偏航通道相軌跡運行情況

采用基于干擾力矩辨識的高精度非線性姿態(tài)控制方法時，飛行器落點縱向偏差為0.30 m，橫向偏差為0.20 m。圖9、圖10給出了末修過程中俯仰和偏航姿態(tài)角跟蹤程序角情況。

圖9 末修過程中俯仰姿態(tài)角與俯仰程序角

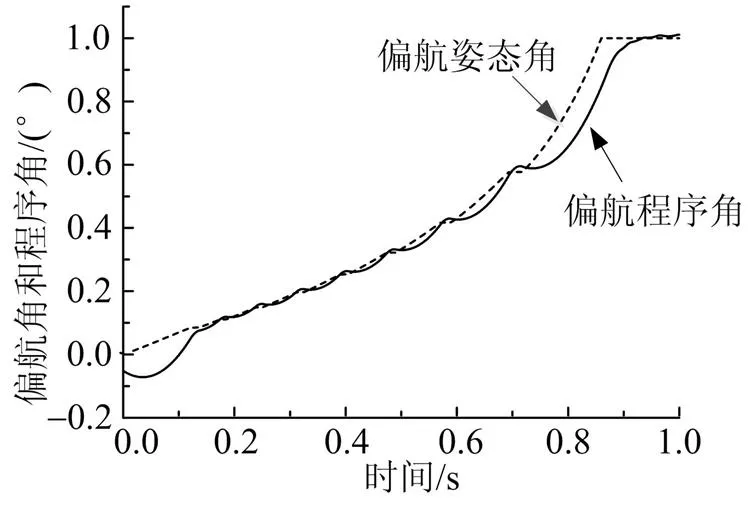
圖10 末修過程中偏航姿態(tài)角和偏航程序角

圖11和圖12給出了末修過程中俯仰和偏航通道姿態(tài)相軌跡運行情況。

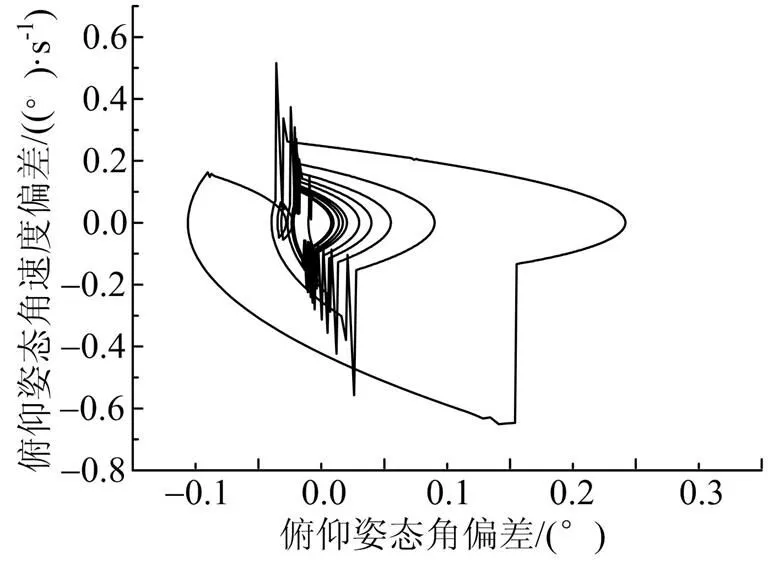
圖11 俯仰通道相軌跡運行情況

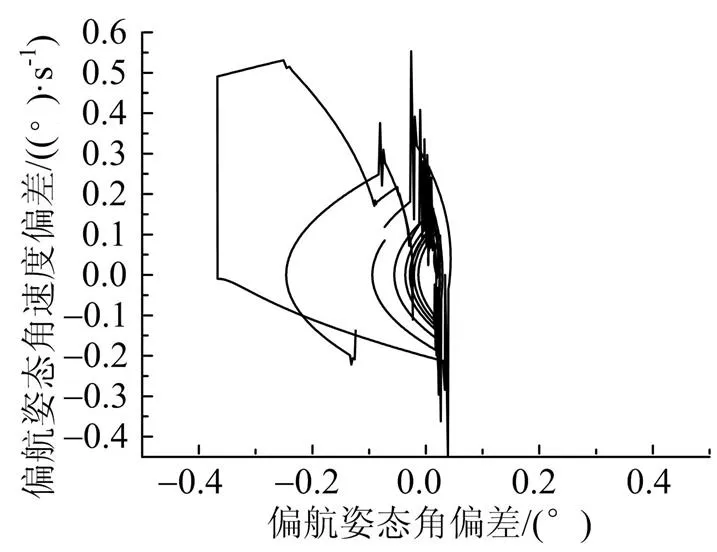
圖12 偏航通道相軌跡運行情況

由圖9至圖12可以看出，末修過程中，俯仰和偏航姿態(tài)角跟蹤程序角比較準確，姿態(tài)角偏差較小，且極限環(huán)環(huán)繞原點。

采用兩種控制律對應的仿真結果對比如表1所示。由表1可見，在噴管開啟次數(shù)和開啟時間基本保持不變的情況下，通過采用基于干擾力矩辨識的高精度非線性姿態(tài)控制方法，可有效改善姿態(tài)角跟蹤程序角情況，降低姿態(tài)角偏差對閉路制導過程的影響，提高飛行器落點精度。

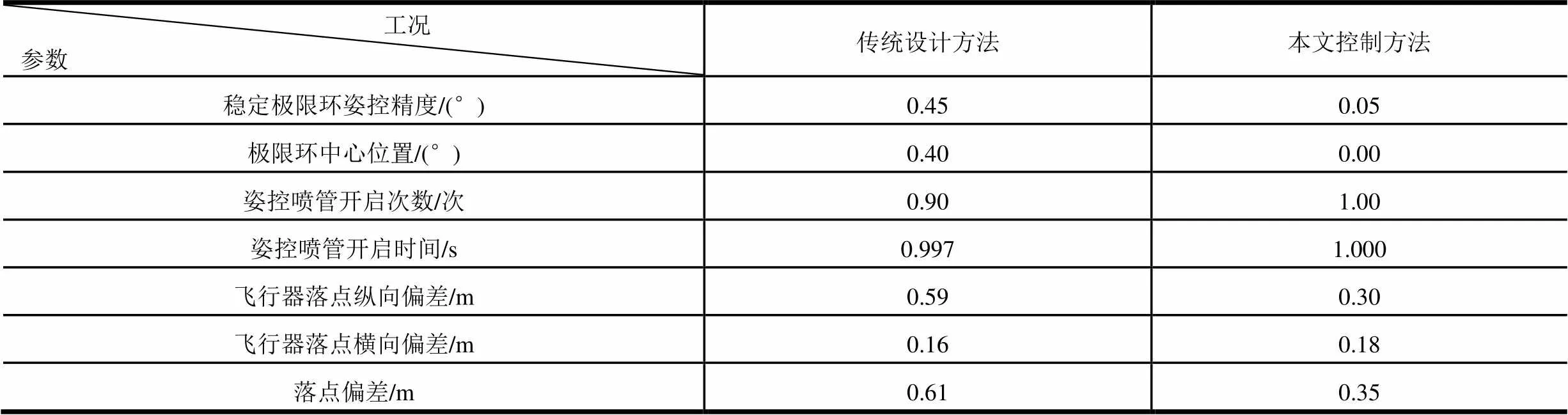
表1 典型工況仿真結果對比

為進一步確定基于干擾力矩辨識的高精度非線性姿態(tài)控制方法的有效性。以某型號為例，分別按傳統(tǒng)開關線設計方法和基于干擾力矩辨識的高精度非線性姿態(tài)控制方法進行制導方法誤差評估。采用模擬打靶法，按照統(tǒng)計的均值加2.7σ取值，兩種控制律下分別仿真計算1 000條彈道，統(tǒng)計結果比較如表2所示。由表2可以看出，采用基于干擾力矩辨識的高精度非線性姿態(tài)控制方法后，可將制導方法誤差降低25%。

表2 制導方法誤差模擬打靶結果對比

5 結 論

本文針對飛行器末修閉路制導飛行段姿控系統(tǒng)非線性設計問題，基于傳統(tǒng)開關線控制情況下極限環(huán)特性，分析了傳統(tǒng)開關非線性設計方法的不足，推導了存在干擾力矩時開關非線性控制系統(tǒng)極限環(huán)模型和飛行器干擾力矩在線辨識模型，提出了基于干擾力矩辨識的高精度非線性姿態(tài)控制方法。仿真結果表明，采用本文提出的設計方法后，在噴管開啟次數(shù)和開啟時間基本保持不變的情況下，可有效改善姿態(tài)角跟蹤程序角情況，降低姿態(tài)角偏差對閉路制導過程的影響，提高飛行器落點精度。

[1] 陳世年. 控制系統(tǒng)設計[M]. 北京: 中國宇航出版社, 2009.

[2] 龍樂豪. 總體設計(中)[M]. 北京: 中國宇航出版社, 2001.

[3] 孫趙根. 最優(yōu)非線性控制技術在導彈控制中的研究與應用[J]. 航天控制, 2005, 23(1): 41-44.

[4] 于桂杰. 基于龍格庫塔法的預測閉路制導方法研究[J]. 航天控制, 2008, 26(5): 41-49.

[5] 馬清華. 利用沖量改進閉路制導研究[J]. 彈箭與制導學報, 2004, 24(4): 302-304.

[6] Gath P F, Calise A J. Optimization of launch vehicle ascent trajectories with path constraints and coast arcs[J]. Journal of Guidance, Control and Dynamics, 2001, 24(4): 296-304.

[7] Calise A J, Melamed N, Lee S. Design and evaluation of three-dimensional optimal ascent guidance algorithm[J]. Journal of Guidance, Control and Dynamics, 1998, 21(6): 867-875.

[8] 王繼平. 一種新的閉路制導導引方法[J]. 航天控制, 2007, 25(5): 58-61.

[9] 馬丹山. 閉路制導推力方向研究[J]. 飛行力學, 2005, 23(3): 64-66.

[10] 胡躍明. 變結構控制理論與應用[M]. 北京: 科學出版社, 2003.

[11] 殷春武. 物理約束下的反演自適應姿態(tài)控制[J]. 西北工業(yè)大學學報，2016, 34(2):281-286.

[12] 李昭瑩. 高超聲速飛行器非線性魯棒控制律設計[J]. 控制理論與應用，2016, 33(1): 62-69.

[13] 王曉東. 閉路制導下提高姿態(tài)控制精度方案研究[J]. 航天控制, 2002(4): 33-45.

[14] 張艷. 在軌航天器非線性姿態(tài)控制系統(tǒng)穩(wěn)態(tài)特性研究[J]. 導彈與航天運載技術, 2012(4): 10-14.

High Precision Nonlinear Attitude Control Method Based on Identification of Disturbing Torque

Wang Yong, Zhang Yan, Xue Hui, Li Yan-jun, Tan Peng-shuo

(Beijing Institute of Astronautical Systems Engineering, Beijing, 100076)

During the terminal correction segment of ballistic vehicle, attitude control nozzle is often used for attitude tracking and stabilization, thus the accuracy of attitude control system directly affects the fall point accuracy. Because of the disturbing torques, systemic errors exist when using traditional diagonal on-off control method, which will influence the terminal correction of ballistic vehicle. In order to solve this problem, this article proposes a high precision nonlinear attitude control method based on the limit cycle model and disturbing torque identification model. Simulation results illustrate that when using this nonlinear attitude control method, the accuracy of attitude control can improve almost ninety percent and the fall point accuracy can improve almost twenty five percent comparing to traditional method.

Ballistic vehicle; Nonlinear attitude control; Limit cycle; Identification of disturbing torque

1004-7182(2017)06-0042-06

10.7654/j.issn.1004-7182.20170610

V433

A

2016-12-15；

2017-01-19

王 勇（1987-），男，工程師，主要研究方向為飛行控制