基于ABAQUS的柵格翼展開試驗動力學分析

冉振華，曾杜娟，黎漢華，邵業濤

?

基于ABAQUS的柵格翼展開試驗動力學分析

冉振華，曾杜娟，黎漢華，邵業濤

（北京宇航系統工程研究所，北京，100076）

通過對柵格翼地面展開試驗運動過程進行理論分析，并結合有限元分析方法分析了柵格翼展開過程中結構強度和增大鉸鏈力矩對展開時間及結構強度的影響。結果表明，柵格翼展開至限位時，柵格翼與殼段接觸點和柵格翼根部柵格位置應力遠大于靜強度分析結果，增大柵格翼鉸鏈力矩對柵格翼展開時間影響較小，但可明顯降低柵格翼展開時刻角速度，減小限位后的沖擊能量。

柵格翼；有限元；動力學分析

0 引 言

柵格翼作為一種新型氣動控制舵面，可折疊安裝在飛行器上，不增大其外形尺寸，飛行中在氣動力作用下自動打開，有利于箭體的存放、運輸和發射，具有弦向壓心變化小，失速舵偏角大，可以在較寬馬赫數數范圍內調整升力線斜率等諸多優點[1~6]，在國外導彈武器及運載火箭中均有應用，中國CZ-2F運載火箭逃逸系統選用柵格翼提供氣動控制力。

柵格翼由外部框架和內部眾多的薄格壁布置成框架形式或蜂窩形式，對加工工藝要求高，其結構強度、穩定性分析、飛行中響應時間對姿控影響、打開過程對結構的沖擊等問題需要進一步研究。

本文通過對柵格翼地面展開試驗運動過程理論分析，并結合有限元分析方法分析了柵格翼展開過程中結構強度和增大鉸鏈力矩對展開時間及柵格翼強度的影響。

1 試驗方案

柵格翼展開試驗系統見圖1，包括箭體模擬件、柵格翼、鉸鏈、分離彈簧、配重等。試驗中，分離彈簧和重物同時解鎖，柵格翼在分離彈簧作用下展開，隨著重力力矩逐漸增大，柵格翼與彈體貼合狀態（0°）轉換為打開狀態（90°）并限位。展開過程中，當柵格翼旋轉角度達到15°時，鉸鏈開始產生阻尼力矩，隨著展開角度的增大，阻尼力距也越來越大，90°時達到最大。

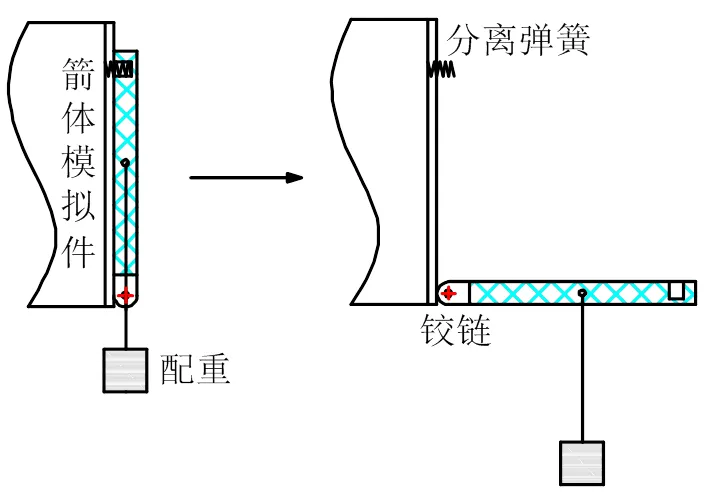
圖1 柵格翼展開試驗示意

柵格翼、殼段材料為ZL205A，鉸鏈及轉軸材料為45鋼，配重模擬氣動力矩，根據風洞吹風結果，按350 ~540 kg逐級加載，承力點距旋轉鉸鏈650 mm。

2 柵格翼展開過程動力學分析

分別對重物和柵格翼進行受力分析[7]，試驗過程柵格翼打開過程動力學方程組如下：

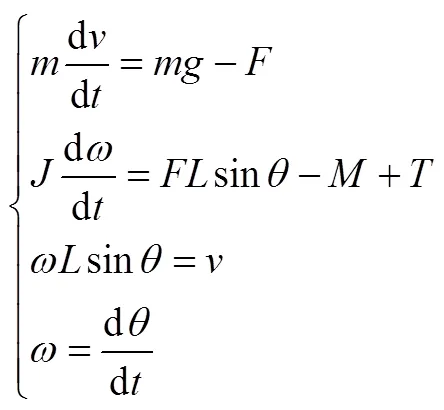
整理為關于打開角度的二階非線性微分方程：

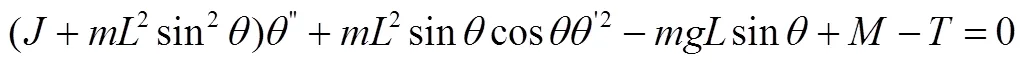
對式（2）進行求解，可求得柵格翼打開角度及角速度隨時間的變化情況分別如圖2~ 4所示，掛載不同重物時打開時間與柵格翼展開時刻角速度見表1。

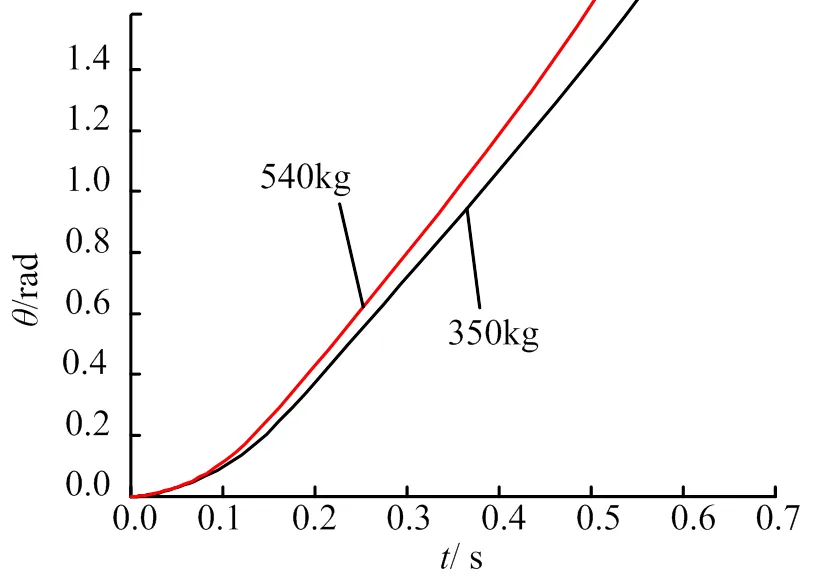
圖2 柵格翼角度隨時間變化情況

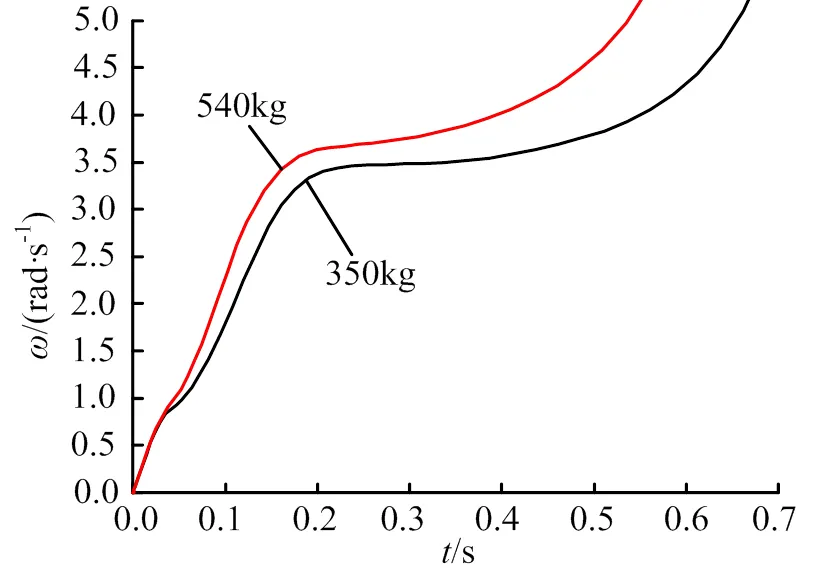
圖3 柵格翼角速度隨時間變化情況

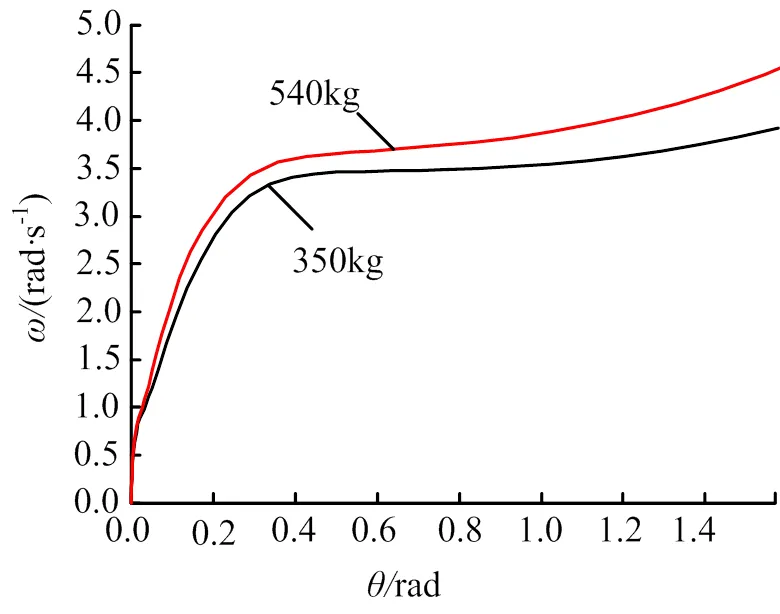
圖4 柵格翼角速度隨角度變化情況

表1 柵格翼打開時間與展開時刻角速度

3 試驗過程有限元分析

3.1 有限元分析模型

本文采用ABAQUS6.11，考慮材料的非線性及幾何非線性，對試驗工況進行隱式結構動力學分析[8]，分析中采用N-mm-s單位制，對殼段及柵格翼結構進行整體建模，模型中各部分結構均采用六面體實體單元模擬，單元類型C3D8I，網格數量80萬，對鉸鏈及接觸位置網格適當加密。采用面面接觸算法來模擬連接螺栓與基座及柵格翼與基座的連接關系。有限元模型見圖5、圖6。

圖5 整體有限元模型

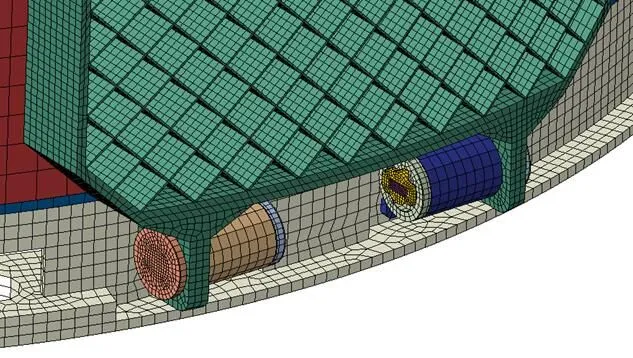
圖6 柵格翼與殼段的連接

根據試驗工況，在重物加載工裝上施加集中力載荷=3 500 N，對柵格翼施加初始角速度，分離彈簧與鉸鏈阻尼采用Hinge進行模擬，并考慮彈簧和鉸鏈的非線性。對模型整體施加重力場，模型中殼段與工裝四處連接位置設置固定邊界條件。

3.2 有限元分析結果

圖7為柵格翼打開情況示意，第1次打開至90°過程中，隨展開角度增大，角速度逐漸增大，繼續打開至與殼段發生碰撞后柵格翼小幅反彈，如此反復多次后停止。

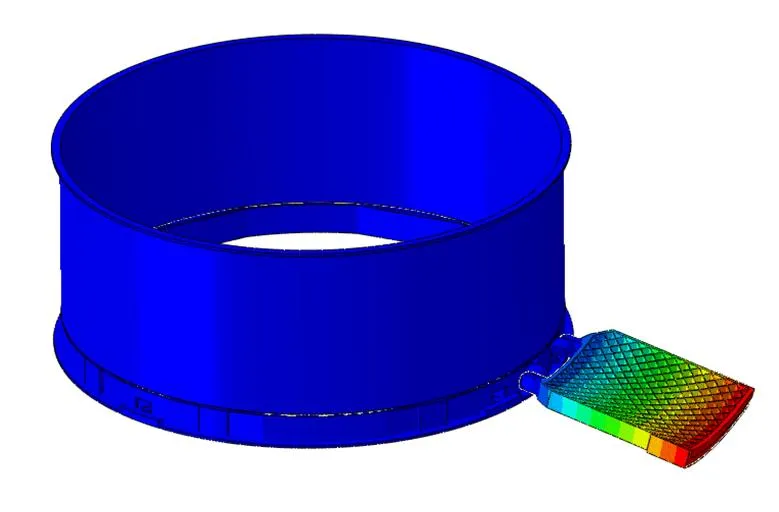
圖7 柵格翼打開情況示意

柵格翼第1次達到90°后0.095 s時柵格翼動能最小，該時刻柵格翼與殼段發生碰撞時兩者的應力應變達到最大值，對應柵格翼、殼段應力分別如圖8、圖9所示，結果表明，柵格翼最大塑性應變出現于與殼段接觸位置，除此之外柵格翼根部靠近轉軸2個柵格上塑性應變最大，為貫穿性屈服，應變值已達到材料ZL205A發生斷裂時塑性應變，遠大于靜強度分析中最大應力265 MPa的分析結果；殼段最大塑性應變出現于柵格翼與殼段接觸位置，塑性應變值為5%。

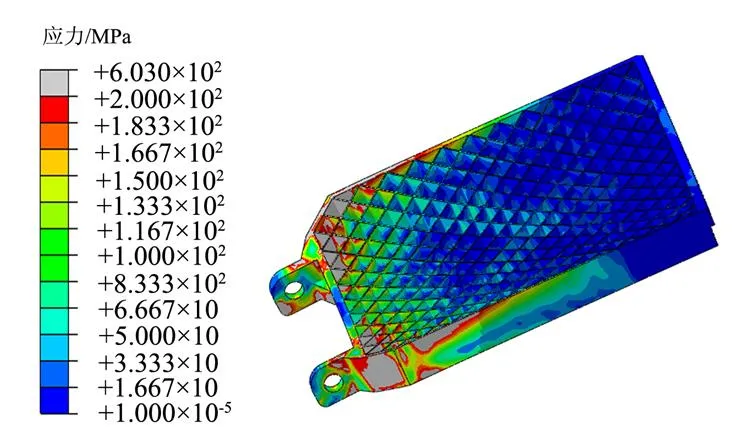
圖8 柵格翼Mises應力

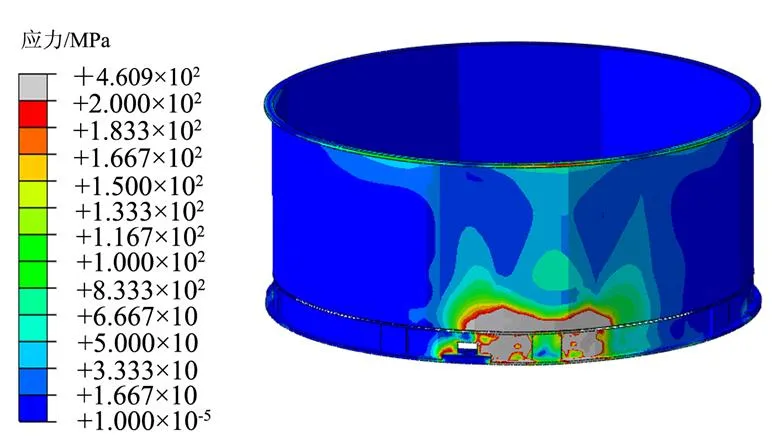
圖9 殼段Mises應力

4 鉸鏈阻尼力矩對柵格翼打開過程影響分析

為解決試驗中柵格翼和鉸鏈破壞問題，在不改變柵格翼和殼段基礎上，盡量通過調整鉸鏈阻尼來實現柵格翼的安全打開，同時盡量減小對柵格翼打開時間的影響。

4.1 鉸鏈阻尼力矩對運動情況影響

假定鉸鏈阻尼初始作用點15°位置不變，增大鉸鏈阻尼力矩（15°~90°區間內阻力力矩，隨角度線性變化）對柵格翼打開時間及展開時刻角速度的影響，分別如圖10、圖11所示，增大鉸鏈力矩各工況柵格翼打開時間及展開時刻角速度見表2。

分析結果表明，增大鉸鏈力矩對柵格翼展開時間影響較小，但可明顯降低柵格翼展開時刻角速度，鉸鏈增大至力矩2 400 N·m展開試驗中測得展開時間為0.6 s，角速度為3.02 rad/s，與本文計算結果基本吻合。

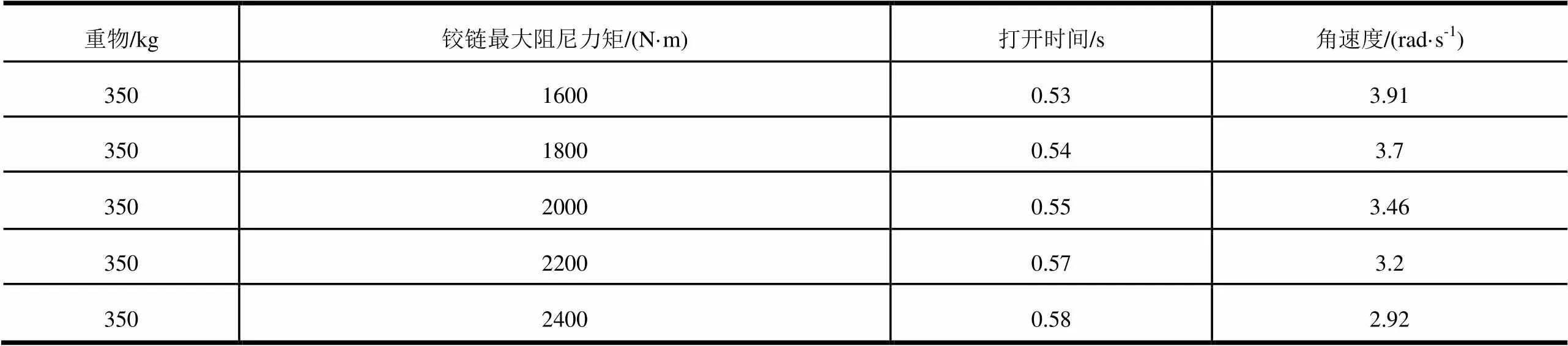
表2 柵格翼打開時間與展開時刻角速度

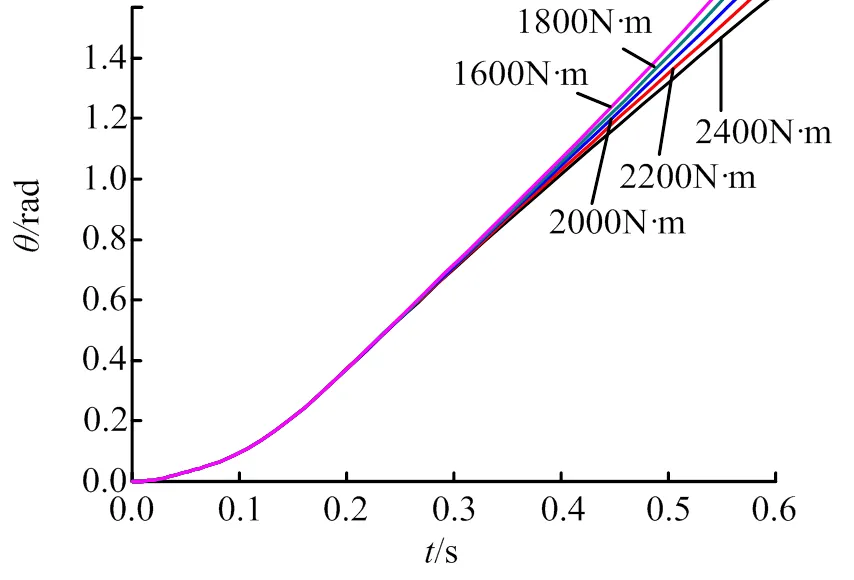
圖10 柵格翼角度隨時間變化情況

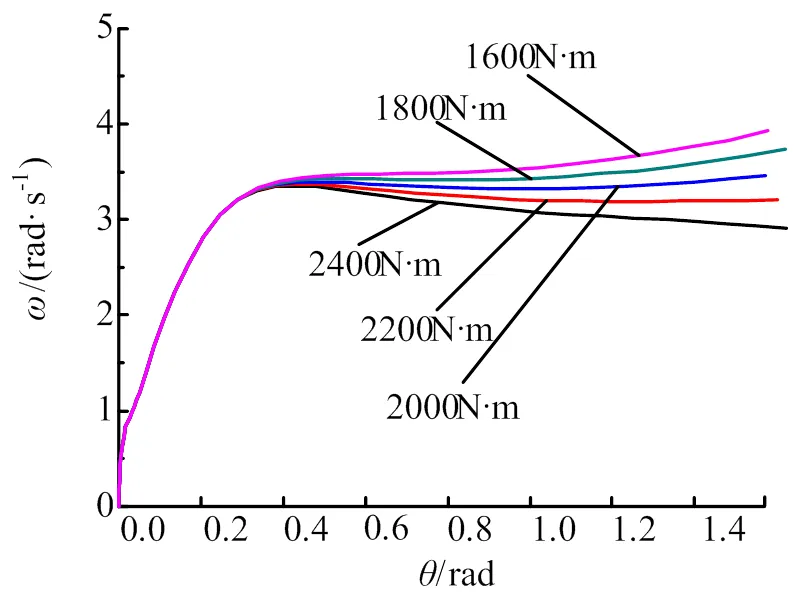
圖11 柵格翼角速度隨角度變化情況

4.2 阻尼力矩增大至2 400 N·m有限元仿真結果

柵格翼動能最小時柵格翼、殼段應力分別如圖12、圖13所示，結果表明，柵格翼最大塑性應變值為3%，殼段最大塑性應變值為1.3%，小于材料ZL205A發生斷裂時塑性應變，主要結構最大塑性應變較原方案減小約25%~40%，可以滿足試驗要求。

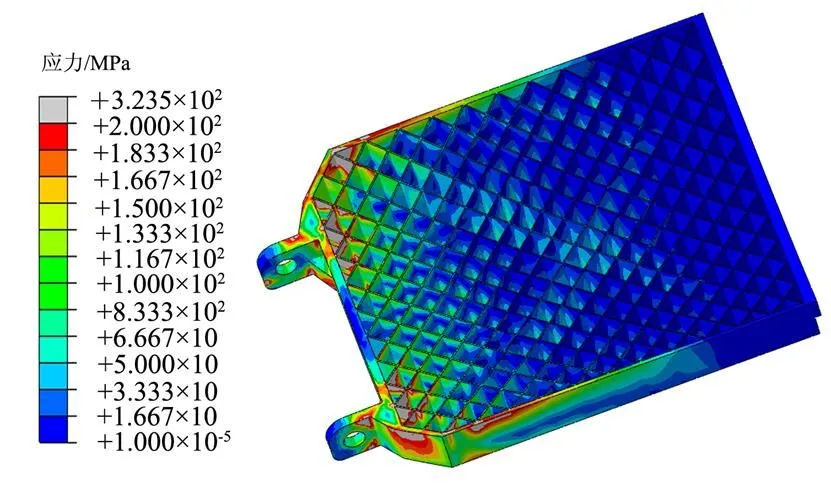
圖12 柵格翼Mises應力

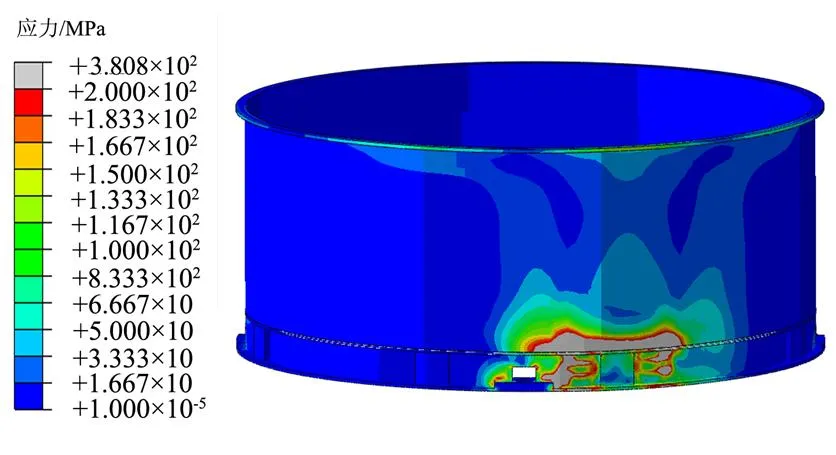
圖13 殼段Mises應力

5 結 論

本文通過建立柵格翼打開動力學方程，并結合有限元方法對柵格翼展開試驗中展開過程及零件結構強度進行了隱式動力學仿真分析，分析結果表明：

a）柵格翼展開至限位時，柵格翼與殼段接觸點和柵格翼根部柵格位置應力遠大于靜強度分析結果，參數選擇不合理將導致結構在該位置發生塑性斷裂，柵格翼試驗中需要重點關注該位置的應力應變；

b）不改變主要結構的情況下，增大鉸鏈阻尼力矩對柵格翼展開時間影響較小，但可以顯著減小柵格翼撞擊限位時的角速度；

c）有限元分析結果表明，適當增大鉸鏈阻尼力矩可顯著減小柵格翼展開限位后的沖擊能量，減小柵格翼和殼段應力。

[1] Fournier E Y. Wind tunnel investigation of grid fin and conventional planar control surfaces[R]. AIAA2001-0256, 2001.

[2] Washington W D, Miller M S. Grid fins-a new concept for missile stability and control[R]. AIAA-93-0035, 1993.

[3] James D, Milton E, Vaugh Jr. Subsonic flow CFD investigation of canard-controlled missile with planar and grid fins[R]. AIAA2003-27, 2003.

[4] 黎漢華, 石玉紅. 柵格翼國內外研究現狀及發展趨勢[J]. 導彈與航天運載技術, 2008(6): 27-30.

[5] 雷娟棉, 吳小勝, 吳甲生. 格柵尾翼(舵)外形參數對氣動特性的影響[J].北京理工大學學報, 2007, 27(8): 675-679.

[6] 陳少松, 徐琴, 王福華. 格柵翼組合體的超音速氣動特性研究[J]. 彈道學報, 2000, 12(2): 50-54.

[7] 程靳. 理論力學[M]. 北京: 高等教育出版社, 2009.

[8] 王虎; 顧克秋. 牽引火炮非線性有限元隱式動力學分析[J]. 南京理工大學學報, 2006, 30(4): 462-466.

Dynamic Analysis of Grid Wing Expansion Test Based on ABAQUS

Ran Zhen-hua, Zeng Du-juan, Li Han-hua, Shao Ye-tao

(Beijing Institute of Astronautical Systems Engineering, Beijing, 100076)

The influence of structural strength and hinge moment on the opening time and structural strength of lattice wing is analyzed by theoretical analysis and finite element analysis. The results show that the stress of the grid wing and shell is much greater than that of the static strength analysis. The increase of the hinge moment has little effect on the lattice wing opening time, but it can reduce the angular velocity of the grid and reduce the impact energy.

Grid wing; Finite element; Dynamic analysis

1004-7182(2017)06-0098-04

10.7654/j.issn.1004-7182.20170621

V421.6

A

2016-10-23；

2017-05-23

冉振華（1987-），男，工程師，主要研究方向為運載火箭動力系統總體設計