基于最小二乘法的磁力計誤差補償與校準
,,,,
(重慶郵電大學 光電信息感測與傳輸技術重慶市重點實驗室,重慶 400065)
0 引言
行人自主導航系統是指能夠實時地提供行人前進方向、當前位置以及速度參數的系統[1],硬件平臺集成了三軸加速度計、三軸磁力計和三軸陀螺儀等傳感器。其中磁力計在行人自主導航系統中用于提供絕對航行信息[2],而航向的精度直接決定著系統定位的精度。在實際應用中,傳感器的固定偏差和隨機誤差將嚴重影響數據融合的精度[3],因此對傳感器數據進行濾波、誤差校準、標定等操作是十分重要的。
傳統的校準方法存在計算量大、操作復雜、不易實現等缺陷[4]。例如梁益豐使用總體八位置法對磁力計進行確定性誤差參數標定,補償精度較高,但需要給出正確的參考方向才能進行校準,不適用于實際使用[5];Fang J. 基于約束最小二乘法的橢球擬合的磁羅盤校準,但只能在沒有磁干擾下使用[6];Bonnet S. 通過采集傳感器數據進行標定,利用橢球擬合可實現磁力計粗略校準,但未考慮傳感器自身噪聲影響,精度較低[7]。
因此本文設計了一種基于最小二乘法和“8”字校準法對磁力計零偏進行實時校準的方法,通過仿真和實驗驗證,該算法有效地解決了磁力計誤差補償問題,具有較強的魯棒性。
1 確定性誤差補償模型
MEMS慣性傳感器的誤差主要可分為確定性誤差和隨機誤差[8-10]。確定性誤差包括固定偏差、比例誤差和非正交誤差,可通過標定實驗來消除。對于隨機誤差,基于其慢時變、非平穩特性,需建立隨機誤差補償方程,通過算法完成誤差實時補償。
磁力計除了上述傳感器本身產生的誤差外,還易受到外界磁場環境的干擾,主要分為硬磁干擾和軟磁干擾[11-13]。硬磁干擾是指磁力計受到永磁鐵或被磁化的物體產生的磁場干擾引起的誤差。軟磁干擾是指軟鐵材料被當地的地磁場磁化后產生的磁場引起的干擾,如電纜可以產生很強的磁場。在實際測試中發現軟磁干擾的影響較小且比較隨機,因此可以忽略對其的校準。
由于傳感器的確定性誤差一般比較穩定,因此可以通過標定的方法求得相應的參數,將參數帶入到誤差校準方程中,從而消除傳感器的確定性誤差。圖1所示為傳感器的誤差補償模型,式(1)為補償方程。
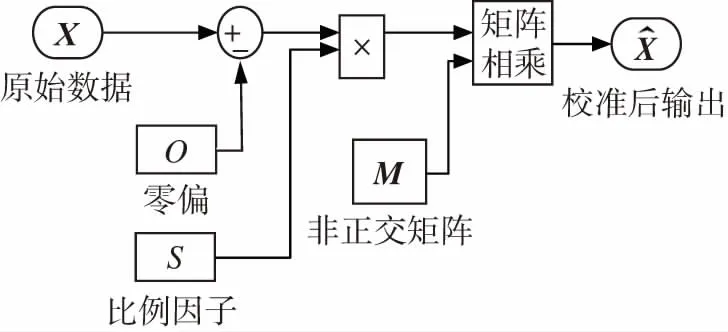
圖1 傳感器誤差補償模型Fig.1 Sensor error compensation model
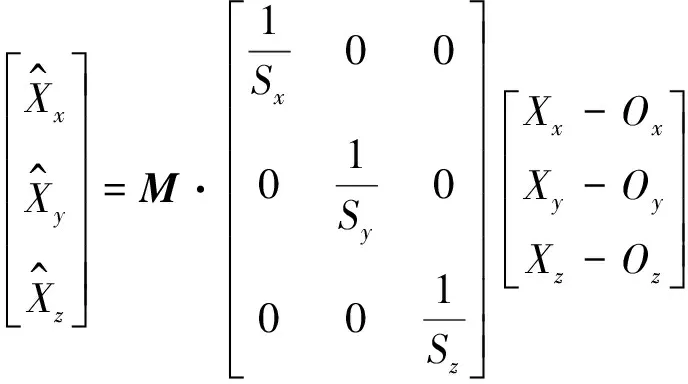
(1)
式中,Ox、Oy和Oz分別為傳感器x、y和z軸上的固定偏差(也叫零偏),Sx、Sy和Sz分別為傳感器在x、y和z軸上的比例誤差因子,M為3×3的非正交誤差矩陣。因此,零偏O、比例誤差因子S和非正交誤差矩陣M就是需要確定的誤差校準參數。
當外界存在的磁場環境相對穩定時,磁干擾對磁力計所產生的零偏值是固定的。然而,行人是流動的,當外界環境改變時,相應的零偏值也會發生變化,這時需要采用自動校準的方法對磁力計的零偏進行更新。
2 利用最小二乘法修正磁力計零偏
若將式(1)中的非正交誤差和比例誤差忽略掉,則可簡寫為
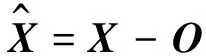
(2)

(3)
第i個測量值的誤差為
(4)
式中,Ox、Oy和Oz為磁力計對應的零偏向量O的元素
(5)
式中,Xx、Xy和Xz為磁力計測量值向量X的元素
(6)
式(4)寫成矩陣形式為
(7)
假設有N組測量值用于計算參數零偏,由于式(7)中含有4個未知量,因此N必須大于或等于4,則式(7)可寫成
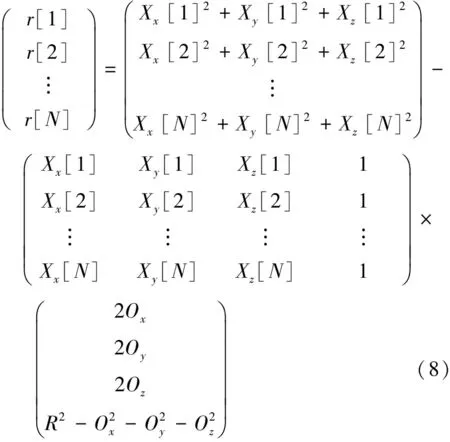
r=Y-Aβ
(9)
式中,Y是只與測量值有關的向量
(10)
A是只與測量值有關的矩陣
(11)
β則是需要被估計的向量
(12)
根據最小二乘估計,需要通過利用一系列磁力計的測量值X和合適的零偏參數O使誤差的平方和為最小。因此有
rTr=(Y-Aβ)T(Y-Aβ)
(13)
代價函數J=rTr可展開為
J=YTY-2βT(ATY)+βT(ATA)β
(14)
求J關于β的導數,并令結果為零,則有
(15)
則最小二乘估計由式(16)決定
β=(ATA)-1(ATY)
(16)
通過以上推導過程可以發現,在進行磁力計的零偏校準時,只需要將測得的N組磁力計數據代入到式(16)便可得到零偏O。
3 “8”字校準法實時校準
然而,在使用磁力計進行測量時,需要采用不同角度方向上的測量值,求得的β才是有意義的。在短時間內得到覆蓋所有角度的磁力計測量值可通過“8”字校準法,如圖2所示。因為測量值要在空間上有一定的不相關性,也就是說這些點要足以約束一個橢球面。如果在空間中隨便轉幾下,得到的測量值可能會在空間上相關,或是不相關性不強,會使校準無法進行或是誤差較大。繞“8”字可以使磁力計收集到不同方向的地磁參數,即原則上盡量多地讓設備的法線指向一個立體空間的所有8個象限,然后根據其反饋回來的數值計算方向,這樣的數據來源比較準確。

圖2 “8”字校準示意圖Fig.2 Schematic diagram of figure“8”calibration
將硬件測試平臺按照圖2做“8”字旋轉后,得到了磁力計的原始數據,如圖3所示,在三維的圖上顯示出一個球體,但球心偏離了坐標原點,說明磁力計存在著零偏誤差。通過加速度計計算得到的橫滾角和俯仰角篩選出N=216組磁力計數據,利用這些數據根據式(16)即可求解零偏值。
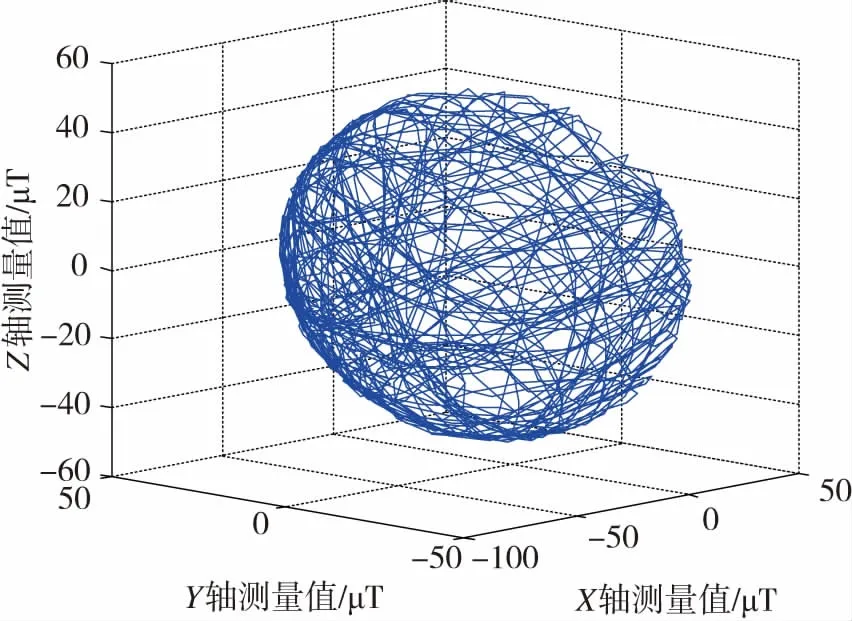
圖3 “8”字旋轉后磁力計數據三維分布圖Fig.3 Three dimensional distribution of magnetometer data after rotation of figure “8”
4 實驗驗證
本文采用華為的智能手機作為磁力計校準的硬件測試平臺。該智能手機集成的MARG傳感器包含三軸加速度計(ST LIS3DH)、三軸磁力計(AKM8963)和三軸陀螺儀(ST L3G4200D)。表1給出了傳感器的型號與參數。
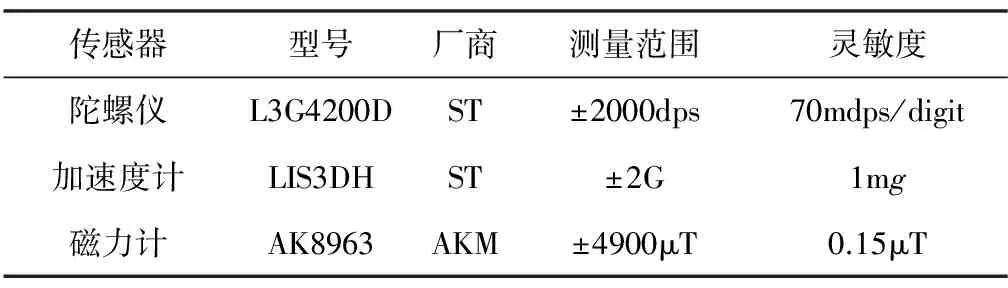
表1 傳感器型號與參數
圖4所示為手機上安裝傳感器的坐標軸方向,在整個實驗過程中行人均采用手持智能手機的方式進行數據采集,手機坐標負y軸指向前進方向,x軸向右,z軸向下。
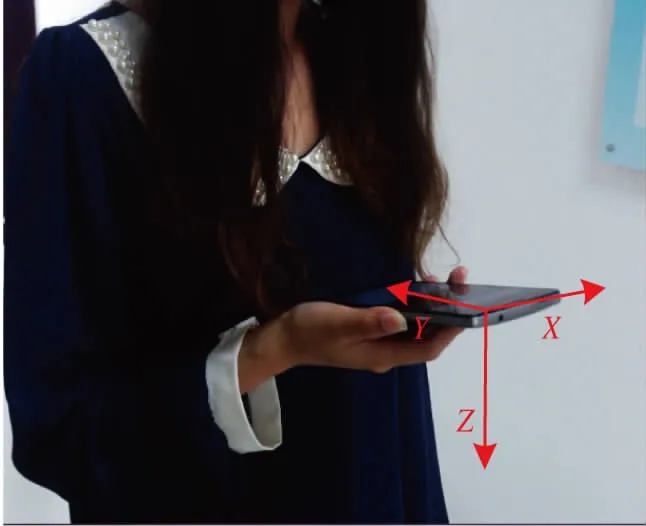
圖4 坐標軸定義Fig.4 Coordinate axis definition
如圖5所示,經過零偏校準后計算的磁力計模值均在49μT(本地磁場強度)附近。從圖5中磁力計模值的原始值可以看出,行人行走時,磁場環境隨著外界環境的改變而變化,相應地磁干擾對磁力計所產生的零偏值也隨之變化,所以磁力計模值輸出波形震蕩較大。因此,可以根據磁力計的模值大小及方差作為磁干擾的判斷條件,若被判定為有磁干擾時,用戶可利用“8”字旋轉方式進行實時校準。
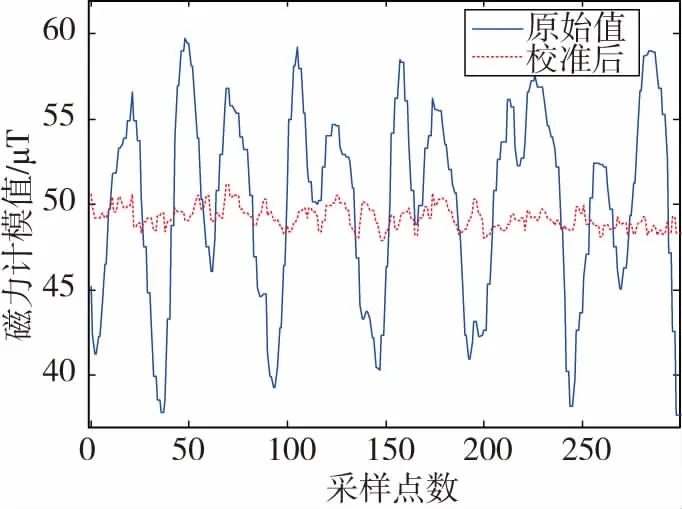
圖5 磁力計數據校準前后對比圖Fig.5 Comparison chart of magnetometerbefore and after data calibration
5 結束語
本文提出了一種基于最小二乘法和“8”字校準法對磁力計零偏進行實時校準的方法。實驗結果表明改進的磁力計誤差補償模型能夠有效地提高磁力計抗磁干擾能力,減小了測量誤差,證明了該誤差補償算法的可行性和有效性。
[1] Jo K, Chu K, Sunwoo M. Interacting multiple model filter-based sensor fusion of GPS with in-vehicle sensors for real-time vehicle positioning[J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(1): 329-343.
[2] 鄒波, 張華, 姜軍. 多傳感信息融合的改進擴展卡爾曼濾波定姿[J]. 計算機應用研究, 2014, 31(4):1035-1038.
[3] 張棟, 焦嵩鳴, 劉延泉. 互補濾波和卡爾曼濾波的融合姿態解算方法[J]. 傳感器與微系統, 2017, 36(3):62-65.
[4] 李勇, 劉文怡, 李杰,等. 基于橢球擬合的三軸磁傳感器誤差補償方法[J]. 傳感技術學報, 2012, 25(7):917-920.
[5] 梁益豐, 許微, 曹勇. MARG傳感器誤差分析與標定方法研究[J]. 艦船電子工程, 2017,37(9):41-45.
[6] Fang J, Sun H, Cao J, et al. A novel calibration method of magnetic compass based on ellipsoid fitting[J]. IEEE Transactions on Instrumentation & Measurement, 2011, 60(6):2053-2061.
[7] Bonnet S, Bassompierre C, Godin C, et al. Calibration methods for inertial and magnetic sensors[J]. Sensors & Actuators A Physical, 2009, 156(2):302-311.
[8] Tedaldi D, Pretto A, Menegatti E. A robust and easy to implement method for IMU calibration without external equipments[C]//2014 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2014: 3042-3049.
[9] Lu J, Lei C. Applied system-level method in calibration validation for personal navigation system in field[J]. Iet Science Measurement & Technology, 2017, 11(1):103-110.
[10] Rohac J, Sipos M, Simanek J.Calibration of low-cost triaxial inertial sensors[J]. Instrumentation & Measurement Magazine IEEE, 2015, 18(6):32-38
[11] 龐學亮, 林春生. 基于遺傳算法三軸磁傳感器校正系數求解[J]. 探測與控制學報, 2017, 39(1):42-45.
[12] 龍禮, 張合. 三軸地磁傳感器誤差的自適應校正方法[J]. 儀器儀表學報, 2013, 34(1):161-165.
[13] 袁廣民, 苑偉政, 秦偉, 等. 強磁干擾環境下磁航向誤差補償技術研究[J]. 航空工程進展, 2012, 3(2): 218-222.

