慣性系統飛行試驗精度檢驗方法

肖正林，陳芳

?

慣性系統飛行試驗精度檢驗方法

肖正林，陳芳

（中國人民解放軍96658部隊，北京 100085）

針對傳統工具誤差分離方法得到的分離結果不夠準確可信的問題，提出了一種利用等效誤差實現對慣性系統精度判定的方法。首先基于主成分分析，定義等效誤差，等效誤差具有獨立、無偏的性質。然后提出基于等效誤差的假設檢驗判斷慣性系統精度是否合格的方法。算例表明采用該方法可以實現慣性系統精度的可信判斷。該方法解決了以往方法誤差大，分析結論可信度不高的問題。

等效誤差；主成分法；精度檢驗；慣性系統

對于采用純慣性制導、慣性/星光復合制導體制的導彈，命中精度主要取決于慣性系統的精度。因此，慣性系統精度滿足指標要求是命中精度定型評定的前提，對飛行試驗中慣性系統精度分析判斷是命中精度評定的一項基礎性工作。

目前飛行試驗慣性系統精度分析的基本方法是：建立慣性系統誤差與飛行試驗遙外差的關系方程，采用估計算法分離誤差，并依據誤差分離結果對各誤差精度滿足情況進行判斷。由于慣性系統誤差的環境函數間強線性相關，導致誤差分離極端困難，為此提出了嶺估計、貝葉斯估計、主成分估計、基于彈道復現估計等方法[1-3]，試圖使誤差分離結果更準確。事實上，上述方法分離結果離準確可信的目標有明顯差距，嚴重影響慣性系統精度的判斷。文中針對該問題開展研究，探討利用可準確分離的等效誤差實現對慣性系統精度判斷的方法，為飛行試驗慣性系統精度分析提供一種新途徑。

1 等效誤差分離與精度判斷方法

1.1 等效誤差分離方法

飛行試驗慣性制導工具誤差都包含在遙外差之中，二者關系為：

Δ=+(1)

式中：Δ為飛行試驗遙外速度差向量，3×1；為慣性系統誤差向量，×1；為速度環境函數矩陣，3×；為外測誤差向量，3×1。

解決這類問題的通常思路是采用最小二乘法估計工具誤差向量，但由于誤差環境函數間強線性相關的影響，最小二乘估計誤差極大，分離結果不可信。主成分估計等改進方法能有效減小估計誤差，但改進方法都是有偏壓縮估計，在減小隨機誤差的同時增大了系統誤差，使估計誤差仍較大，不能滿足精度判斷的要求。為了實現慣性系統精度的可信判斷，文中基于主成分分析法，通過分離等效誤差，并對等效誤差進行統計分析，實現對慣性系統精度的判斷。

在討論時對式（1）作如下處理：誤差環境函數計算時，誤差大小取精度指標（即每個誤差項取其對應的1）；利用外測精度加權。經過處理后的誤差估計正則方程為式（2），得到的估計結果為誤差指標要求的倍數。

[T－1]=T－1Δ(2)

求[T－1]矩陣的特征值和特征向量矩陣。設特征值構成的對角陣為，并按某一閾值將其分為兩部分，設大于閾值的特征值構成的對角陣為1，小于閾值的特征值構成的對角陣為2，對應的特征向量矩陣為1和2，則式（2）可變為：

[111T+222T]=T－1Δ(3)

定義1=1T為等效誤差向量。依據特征向量性質有1T2=0，則由式（3）可得等效誤差向量的估計方程為：

上述推導是在外測精度理想且準確已知的條件下進行的，此時經外測精度加權處理后的外測誤差散布應為1。雖然外測數據提供了精度，但并不理想，實際外測誤差是非平穩、非隨機、非白噪聲的。因此，盡管在建立誤差分離方程時采用了外測精度加權，但由于外測誤差導致等效誤差估計精度與理論精度有差異。下面探討解決該問題的方法仍然基于等效誤差分析方法，具體方法如下。

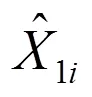
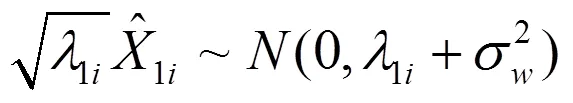
當1i≈0時有：

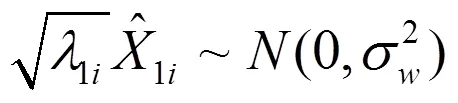
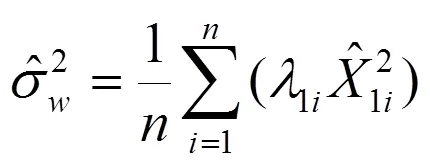
1.2 慣性系統誤差精度判斷方法

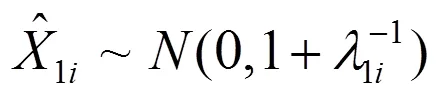
由于每次飛行試驗各等效誤差之間相互獨立，而不同飛行試驗各慣性系統之間相互獨立，因此將所有有效飛行試驗的所有等效誤差估計值放到一起進行綜合判斷。在所有飛行試驗的所有等效誤差判斷0i成立的條件下進行，此時有：

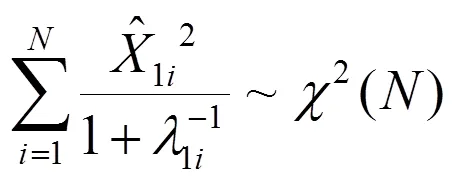
2 應用實例分析

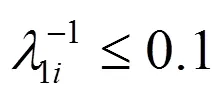
圖1 速度殘差

由圖1可以看出，分離后殘差無明顯系統誤差，表明分離結果已包含了該次飛行試驗該平臺誤差的幾乎全部信息。表1是本次飛行試驗等效誤差分離結果（按特征值由大到小排序）。

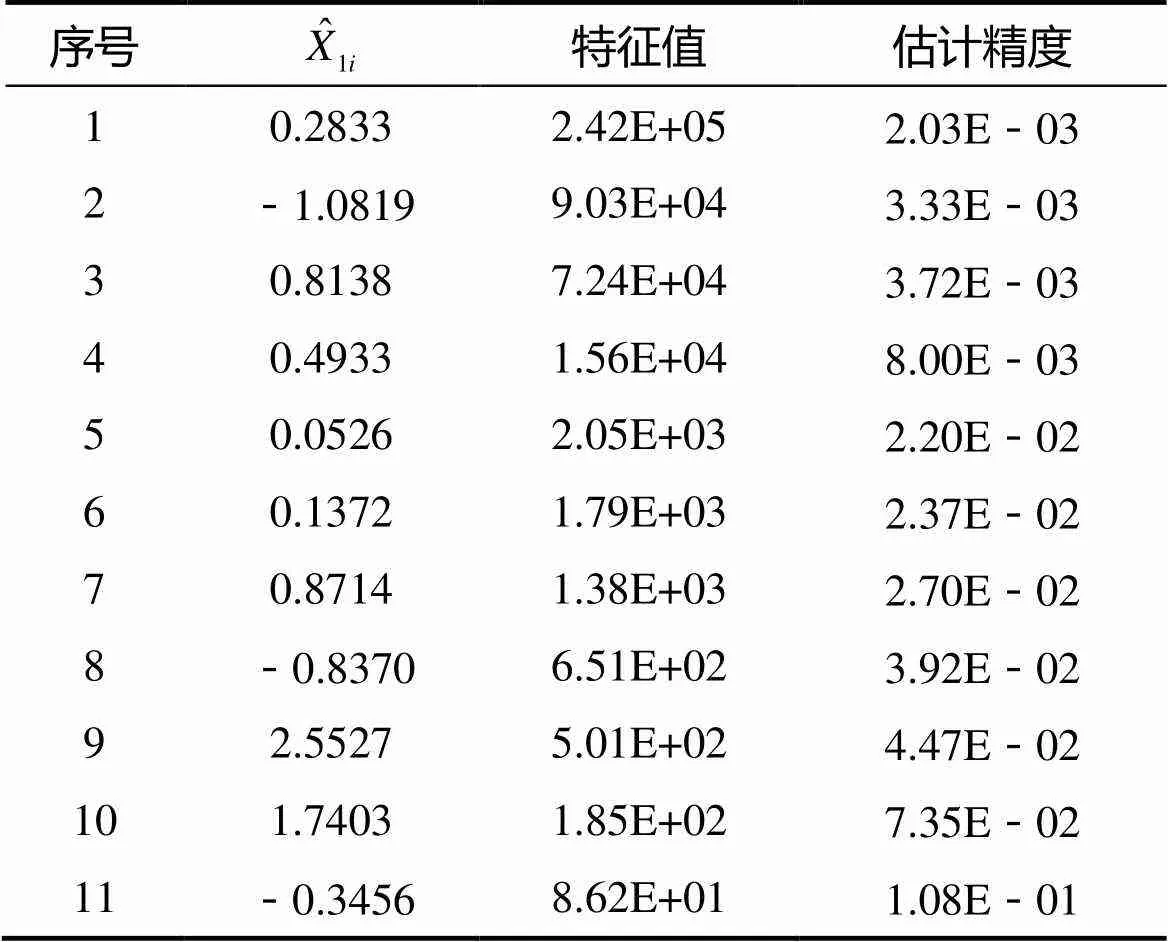
表1 等效誤差分離結果

取置信水平1－=0.99，查表得0.995=2.58，可以得到該平臺飛行試驗精度判斷結果見表2。

由表2可見，該平臺所有等效誤差均判斷合格。下面對誤差進一步判斷。取置信水平1－=0.99，查表得0.012(11) =24.725。由表1數據可求得：

綜合單項判斷與綜合判斷結果可以判斷，該套平臺的精度合格。當有多次飛行試驗時，應綜合所有有效飛行試驗分離結果進行精度的判斷。

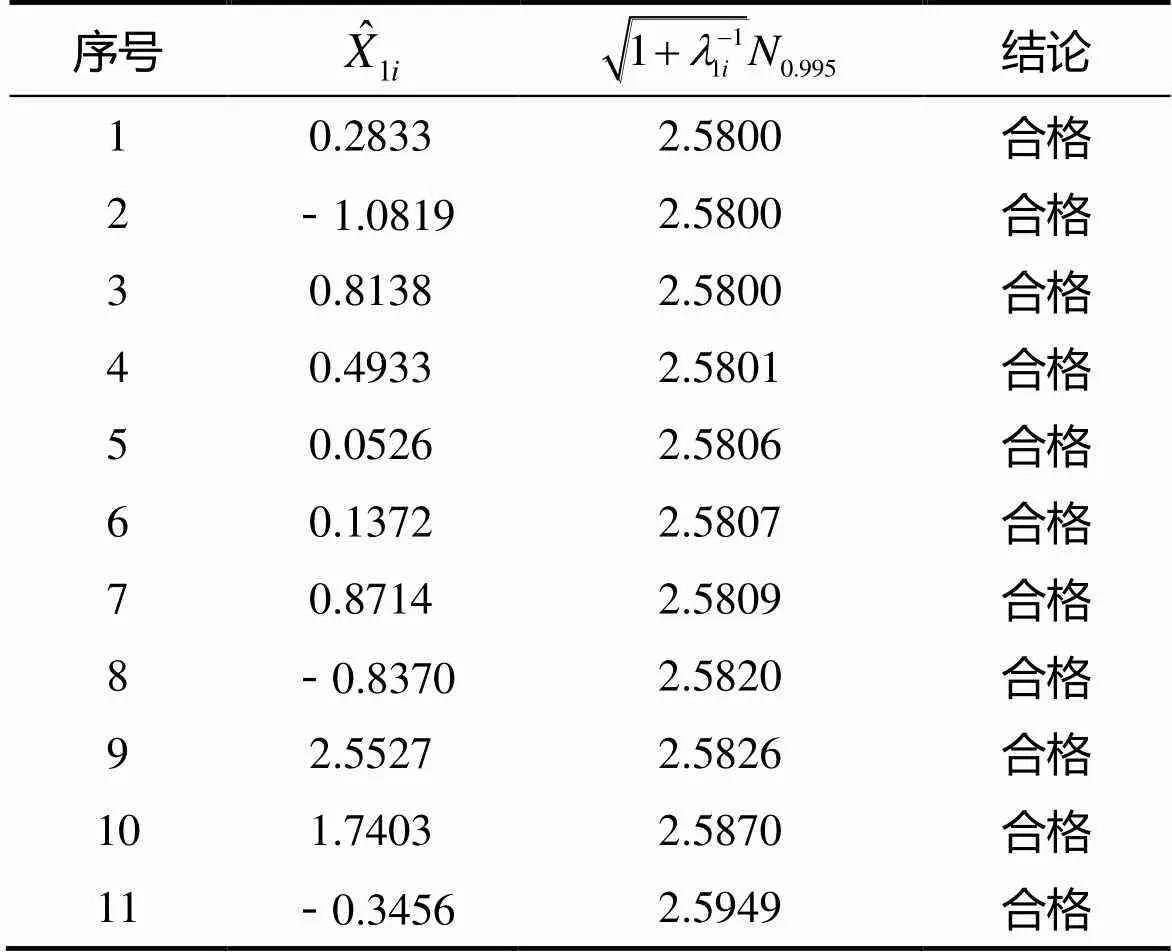
表2 工具誤差精度判斷結果

3 結語

文中利用定義的等效誤差無偏、獨立的優良統計特性，提出了基于等效誤差的假設檢驗判斷慣性系統精度是否合格的方法，可以實現慣性系統精度的可信判斷。

[1] 唐雪梅, 蔡洪, 楊華波, 等. 導彈武器精度分析與評估[M]. 北京: 國防工業出版社, 2015.

[2] 徐德坤, 劉偉, 孟云鶴, 等. 基于進化策略的誤差分離方法[J]. 宇航學報, 2008, 29(1): 352-356.

[3] 徐德坤, 楊華波, 張士峰, 等. 制導工具誤差折合的遺傳主成份法[J]. 航天控制, 2007, 25(6): 22-26.

A Method for Testing Accuracy of Inertial System in Flight Test

XIAO Zheng-linCHEN Fang

(Troop 96658, PLA, Beijing 100085, China)

Aiming at the problem that results obtained by the traditional instrument error separation method are not accurate enough, a method for determining the accuracy of the inertial system by using equivalent error is proposed.Firstly, the equivalent error which was independent and unbiased was defined based on the principal component analysis. Then, a method based on the hypothesis test of the equivalent error was put forward to determine the precision of the inertial system.The example showed that the method can be used to determine the inertial system accuracy credibly.With this method, the problem that the error is large and the credibility is low in the previous approach is solved.

equivalent error; principal component method; precision test; inertial system

10.7643/ issn.1672-9242.2018.01.005

TJ01；V448.25

A

1672-9242(2018)01-0023-03

2017-11-10；

2017-12-02

肖正林（1971—），男，研究員，博士，主要研究方向為導彈控制系統與精確制導技術研究。