方鋼管混凝土柱?鋼梁外環板式節點抗剪性能

別雪夢，李召，管文強，杜國鋒

?

方鋼管混凝土柱?鋼梁外環板式節點抗剪性能

別雪夢，李召，管文強，杜國鋒

(1. 長江大學城市建設學院，湖北 荊州，434023；2. 長江大學 結構工程與防災研究所，湖北 荊州，434023)

為研究方鋼管混凝土柱?鋼梁外環板式節點抗剪性能,以鋼管混凝土柱節點試驗尺寸為參照，建立方鋼管混凝土柱?鋼梁外環板式節點在往復荷載作用下的精細有限元分析模型。該模型考慮材料非線性、混凝土材料在循環荷載下的損傷退化、鋼和混凝土之間的相互作用等因素的影響。通過與試驗結果進行對比分析，驗證該有限元模型具有較好的精度和可靠性。此后研究柱寬厚比、核心混凝土強度、軸壓比和節點核心區高寬比等因素對節點的影響，提出一種方鋼管混凝土柱?鋼梁外環板式節點的核心區剪力?剪切變形恢復力模型。研究結果表明，該模型具有實用性，可為工程設計提供實際依據。

方鋼管混凝土柱?鋼梁外環板式節點；有限元分析；鋼筋混凝土樓板；抗剪性能

方鋼管混凝土柱與鋼梁的剛性連接常采用外環板式節點。外環板節點具有傳力明確、節點區應力分布較均勻、塑性性能好、剛度大和承載力高等優點。目前國內外學者對方鋼管混凝土柱外加強環式節點研究較少[1?6]，且節點破壞模式大部分為梁鉸破壞或節點彎曲破壞，節點剪切破壞模式相對較少。此外對樓板影響下的方鋼管混凝土柱?鋼梁外環板式節點核心區抗剪承載力計算公式以及剪力?剪切變形恢復力模型的研究報道較少。但實際工程中由于樓板的存在導致節點極易發生剪切破壞。因此，本文作者以文獻[7]中的方鋼管混凝土柱?鋼梁外環板式節點(以下簡稱“節點”)為參照，建立考慮材料損傷的節點精細化有限元分析(FEA)模型，對節點在往復荷載作用下的破壞形態和全過程進行分析，并與試驗結果進行對比來驗證該有限元模型的有效性，且在此基礎上對節點進行參數分析。最后基于參數分析結果，提出該類節點的恢復力模型，研究結果可為日后節點抗震計算分析提供有益參考。

1 鋼管混凝土柱?鋼梁節點有限元模型

1.1 有限元模型的建立

1.1.1 材料的本構模型

鋼材的本構關系采用文獻[7]推薦的三折線模型，在有限元軟件中采用塑性模型來描述這一關系。節點涉及鋼管內的核心混凝土和樓板中的普通混凝土，核心混凝土和普通混凝土受壓應力?應變關系分別采用應用較廣的劉威[8]的核心混凝土本構模型和過鎮海[9]的混凝土本構模型，并根據文獻[10]定義了2種彈性模量分別為2.66×104N/mm2和2.8×104N/mm2；2種混凝土受拉應力?應變關系采用GB 50010—2010“混凝土結構設計規范”[11]推薦的混凝土受拉本構模型。在有限元軟件ABAQUS 中混凝土的本構關系通過混凝土損傷塑性模型(簡稱CDP)中輸入混凝土的受壓和受拉應力?應變關系來反映，該模型通過受拉損傷因子t和受壓損傷因子c(0≤t,c≤1)來反映其剛度退化。CDP 模型中損傷變量計算式為

1.1.2 單元、網格和邊界條件

核心混凝土、樓板混凝土、鋼管、鋼梁以及加載板均采用八節點減縮積分實體單元，鋼筋采用兩節點的三維線性梁單元。單元網格劃分采用結構化劃分網格技術，并在保證計算精確度的同時對網格進行調整來提高計算效率；在靠近節點核心區部位進行網格加密(見圖1)。對柱頂對稱中線的，方向平動及，方向轉動進行約束；對柱底對稱中線，，方向平動及，方向轉動進行約束；同時對梁端，方向轉動進行限制。在柱頂按軸壓比以集中力方式施加軸向力；在梁加載端以位移加載方式施加單向荷載或往復荷載(見圖1)。

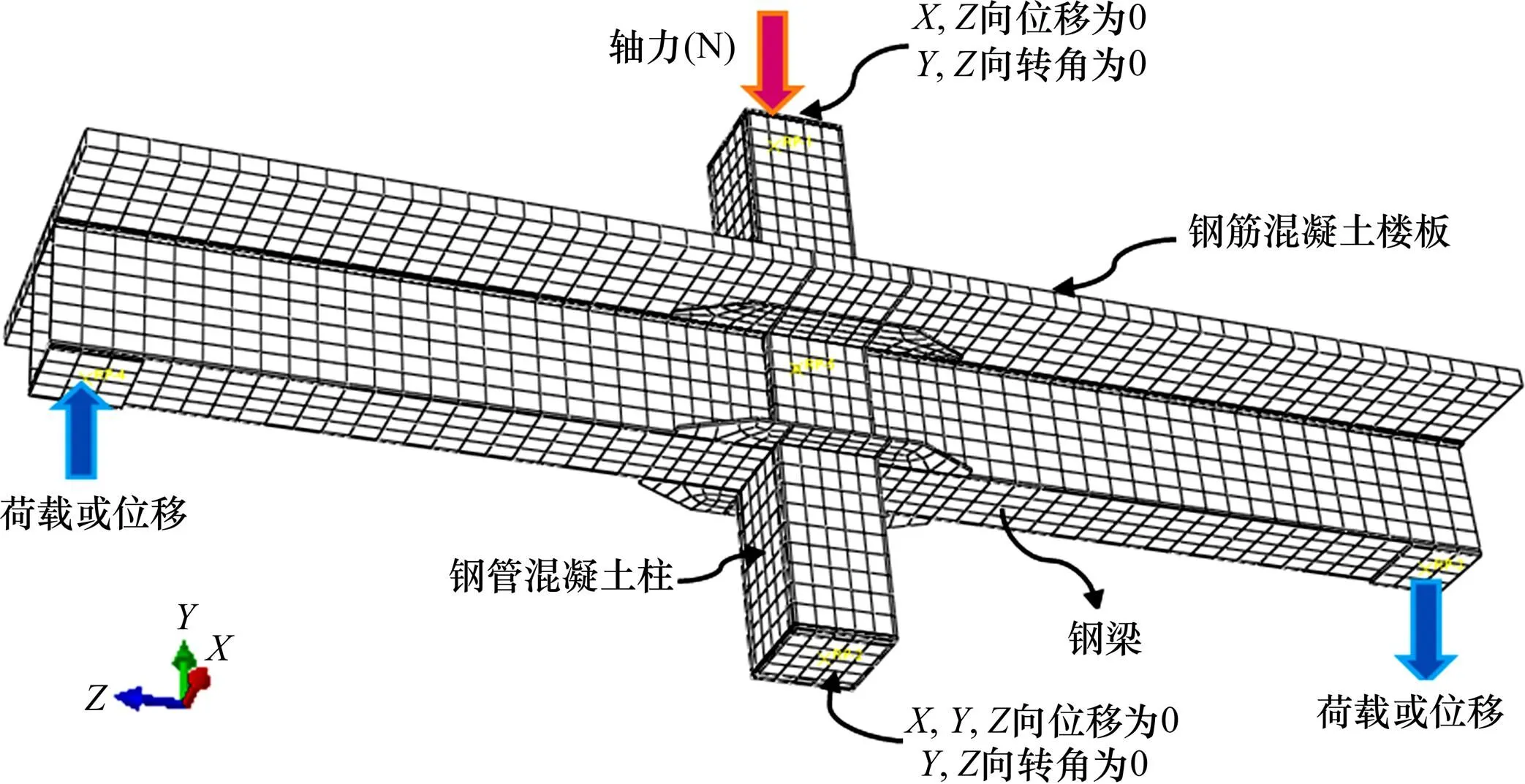
圖1 外環板式節點CFRTJ-4有限元模型

1.1.3 接觸和連接處理

CFST柱的核心混凝土與鋼管之間的接觸面存在切向作用和法向作用。其切向采用庫侖摩擦模型來傳遞剪應力，摩擦因數根據劉威[8]的建議取0.25；法向采用硬接觸。鋼梁和柱，以及鋼梁和樓板之間均采用綁定約束來進行模擬。鋼筋和樓板混凝土之間采用分離式模型中將鋼筋內置于樓板混凝土中的方式來進行分析。

本文所建立的模型考慮了鋼和混凝土的材料非線性、混凝土損傷塑性、由接觸、滑移等引起的邊界條件非線性問題，最終歸結于求解非線性平衡方程組。

1.2 有限元模型的驗證

為驗證上文提及的材料本構模型、單元類型、邊界條件和接觸等設置在節點受力分析中的適用性，本文利用該有限元模型對文獻[7]中帶樓板鋼管混凝土柱?鋼梁外環板式節點CFRTJ-4進行分析，并與試驗結果進行對比。節點CFRTJ-4的材料性能參數見表1和表2，截面尺寸見圖2。其中：柱中核心混凝土和樓板中普通混凝土強度等級分別為C40和C35；柱的鋼管壁厚=8 mm；鋼梁下翼緣鋼板厚8 mm，其他為6 mm；柱軸壓比=0.3，柱總高=1 396 mm，節點核心區高度=291 mm、寬度(即柱寬)=250 mm。

表1 鋼材的材料性能

表2 混凝土的材料性能

1.2.1 在單向荷載作用下節點的數值模擬

節點 CFRTJ-4在單向加載下的梁端荷載?位移(?)計算曲線和核心區剪力?剪切變形(–)計算曲線與試驗骨架曲線進行比較分別見圖3(a)和圖3(b)。由圖3可見：計算曲線與試驗曲線趨勢相近，節點的剪切剛度基本相同。在試驗中由于柱翼緣、腹板拼接焊縫發生破壞，使得曲線出現下降段，剪切破壞并沒有完全形成，而有限元模型較好地模擬了剪切破壞過程，梁端沒有發生局部屈服，因此骨架曲線也沒有明顯的下降段。

單位：mm

(a) P?Δ曲線；(b) V– γ曲線

節點CFRTJ-4在單向加載下的鋼管和核心混凝土Mises應力圖分別見圖4(a)和圖4(b)。由圖4可見：節點破壞時，部分外環板、鋼管、鋼梁翼緣進入屈服狀態；鋼梁根部和柱角存在應力集中，核心混凝土被壓碎；節點剪切破壞及外環板拉斷是節點最終破壞緣由。節點破壞形態與試驗現象相符，說明建立的有限元模型可行性較好。

1.2.2 在循環往復荷載作用下節點的數值模擬

節點CFRTJ-4在循環往復荷載下的?計算曲線和–計算曲線與試驗骨架曲線進行比較分別見圖5(a)和圖5(b)。由圖5可見：節點滯回曲線較飽滿，沒有明顯的捏縮現象；節點塑性變形能力較強，具有很好的抗震性能和耗能能力。計算曲線與試驗曲線吻合較好，說明建立的有限元模型精度較高。

(a) 節點鋼管；(b) 節點核心混凝土

(a) P?Δ曲線；(b) V– γ曲線

節點CFRTJ-4在循環往復荷載下的鋼管和核心混凝土Mises應力圖分別見圖6(a)和圖6(b)。由圖6可見：節點的破壞區域在靠近節點的梁根部位置；鋼梁根部和柱角存在應力集中；節點的鋼梁、外鋼管進入了屈服狀態，核心混凝土被壓碎；節點破壞形態與試驗結果相符，說明建立的有限元模型可行性較好。

(a) 節點鋼管；(b) 節點核心混凝土

2 參數分析

為深入研究節點抗剪性能，本文基于上文模擬較準確的節點CFRTJ-4有限元模型，對節點進行參數分析，為節點實用計算方法和簡化模型的研究奠定基礎。主要參數包括柱的寬厚比()、核心混凝土強度(cu)、柱軸壓比()及核心區高寬比()等，試件參數見表3。表3中：為柱寬，250 mm；寬厚比()通過改變柱的鋼管壁厚()來分析；高寬比()為節點核心區高度()和寬度()的比值，通過改變核心區的高度()來實現；在對高寬比()進行參數分析時，只選取當軸壓比()為0時，不同高寬比(=0.70，1.16和1.94)對節點受力的影響。此表中的CF-G1-1，CF-G1-2，CF-G1-3，CF-G2-1，CF-G2-2和CF-G2-3為后面提出恢復力模型時所用節點。

2.1 寬厚比(B/t)

不同寬厚比()下節點核心區剪力?剪切變形關系(j–j)的計算結果見圖7(a)。由圖7(a)可見：寬厚比()對核心區j–j曲線的影響較為明顯；節點抗剪承載力和強化階段的剛度隨著寬厚比增大而增大。

表3 試件參數

注：CFRTJ-4為試驗節點，其他節點為有限元分析節點

2.2 核心混凝土強度(fcu)

不同核心混凝土強度(cu)下節點核心區j–j的計算結果見圖7(b)。由圖7(b)可見：cu對核心區j–j關系有一定影響，對核心區抗剪剛度的影響不很明顯；核心區抗剪承載力隨著cu的提高而增大。

(a) 寬厚比B/t；(b) 核心混凝土強度fcu；(c) 軸壓比n；(d) 高寬比h/B

2.3 軸壓比(n)

不同軸壓比()下節點核心區j–j的計算結果見圖7(c)。由圖7(c)可見：對試件抗剪承載力有一定影響，對彈性階段剛度影響很小；當＜0.5時，核心區抗剪承載力隨著的增大，有一定程度的提高；但當＞0.5時，抗剪承載力隨著的增大而降低；當從0.6變為0.8時，節點破壞模式從節點域剪切破壞變為柱壓彎破壞。

2.4 高寬比(h/B)

不同高寬比()下節點核心區j–j的計算結果見圖7(d)。由圖7(d)可見：對核心區的抗剪承載力影響較明顯，對曲線彈性階段剛度的影響較明顯；核心區抗剪承載力隨著的提高有所降低。

3 節點的恢復力模型

3.1 核心區剪力?剪切變形恢復力模型

節點恢復力模型是節點整體或組成部分在往復荷載下的力?變形關系，是進行節點彈塑性地震全過程分析的重要前提。疊加鋼管和混凝土的j–j關系來求得核心區整體的j–j關系，是研究核心區j–j曲線的主要方法[13?18]。通常認為，方鋼管混凝土柱?鋼梁外環板式節點抗剪承載力主要由節點核心區混凝土、鋼管腹板以及鋼板框架(由鋼管翼緣與外環板組成)共同提供。但是通過研究結果表明，鋼板框架對節點抗剪承載力的貢獻很小，因此本文不進行討論。節點抗剪承載力主要由鋼管腹板和核心區混凝土(分別以平面抗剪和斜壓桿模式對抗剪做出貢獻)共同承擔。本文所研究節點核心區剪力?剪變(j–j)的下降段并不明顯，因為節點在達到極限承載力后，核心混凝土分擔的剪力下降，但鋼管仍處于強化段，整體的剪力可能還呈上升趨勢。因此，本文作者認為鋼管混凝土柱?鋼梁外環板式節點核心區j–j骨架線可采用圖8的三折線模型，總剪力在達到u后保持不變，模型有彈性段剛度(el)、抗剪屈服承載力(y)、抗剪極限承載力(u)及此時的極限剪切變形(u)共4個參數。

圖8 節點核心區剪力(Vj)?剪切變形(γj)關系

3.1.1 彈性階段剛度(el)

研究結果表明：加載初期，鋼管對核心混凝土的約束較小，外鋼管和核心混凝土的變形基本協調。因此核心區整體剪切剛度(el)可視為鋼管剛度(el,s)和混凝土剛度(el,c)的疊加。鋼管的彈性剪切剛度(el,s)為

式中：s為鋼材剪切模量，根據規范[19]，s=7.9×104N/mm2；vy,p為鋼管屈服時其受剪面積，根據FUKUMOTO等[15]的研究，vy,p=s,p/2，s,p為方鋼管橫截面積，mm2。鋼管屈服時的剪切變形(y,wp)為

鋼管屈服可以看做節點核心區屈服[15]。當節點核心區屈服時，混凝土的彈性剪切剛度(el,c)為

式中：c,y表示變形為y,wp時混凝土承擔的剪力。參數分析表明：軸壓比()對節點核心區彈性階段剛度影響很小，混凝土的彈性剪切剛度(el,c)主要與寬厚比()、核心混凝土強度(cu)和高寬比()有關。引入韓林海[18]定義的約束效應系數(p)來表示寬厚比()和核心混凝土強度(cu)對核心區性能的影響。

圖9(a)所示為c,yFEA/(c,pc,p)與p的關系圖。圖中，c,yFEA表示核心區剪切變形為y,wp時混凝土的剪力；c,p和c,p分別為核心區混凝土的抗壓強度和核心混凝土橫截面積。為消除對el,c的影響，算例的為1.16。由圖9(a)可見：c,yFEA/(c,pc,p)和p的關系可表示為c,yFEA/(c,pc,p)=0.016+0028p。圖9(b)所示為c,yFEA/c,yFEA1.16與的關系圖。圖中，c,yFEA1.16表示核心區剪切變形為y,wp時，核心區高寬比()為1.16的混凝土的剪力。由圖9(b)可見：c,yFEA/c,yFEA1.16和的關系可表示為c,yFEA/c,yFEA1.16=1.7?0.5。總結約束效應系數(p)和高寬比()的影響，c,y=(0.016+0028p)(1.7?0.5)c,pc,p，從而可得到el,c的表達式為

因此，根據疊加原理節點核心區整體彈性剪切剛度(el)為

3.1.2 抗剪極限承載力(u)

節點核心區抗剪極限承載力(u)可看做鋼管極限承載力(s,u)和混凝土極限承載力(c,u)的疊加。其中混凝土承載力(c,u)通過疊加混凝土平面抗剪承載力(c,u1)和斜壓桿模式抗剪承載力(c,u2)得到。通過參數分析表明：寬厚比()、核心混凝土強度(cu)、軸壓比()和高寬比()對核心區抗剪極限承載力(u)影響較大。

總結約束效應系數(p)、高寬比()和軸壓比()的影響，s,u的表達式為

2)混凝土極限承載力(c,u)。混凝土承載力(c,u)通過疊加混凝土平面抗剪承載力(c,u1)和斜壓桿模式抗剪承載力(c,u2)得到。首先分析平面抗剪承載力(c,u1)。圖11(a)所示為c,uFEA/c,f與p的關系圖。圖中，c,uFEA為在極限點時計算的混凝土剪力；c,f為混凝土剪力參考值，c,f=0.3c,pc,p。算例的為0，為1.16。由圖11(a)可見：c,uFEA/c,f和p的關系可表示為c,uFEA/c,f= 0.15+0.1p。圖11(b) 所示為c,uFEA/c,uFEA1.16與的關系圖。圖中，c,uFEA1.16表示核心區高寬比()為1.16，在極限點時計算的混凝土剪力。算例的為0。由圖11(b)可見：c,uFEA/c,uFEA1.16和的關系可表示為c,uFEA/c,uFEA1.16=1.3?0.22。圖11(c)所示為c,uFEA/c,uFEAn0與的關系圖。圖中，c,uFEAn0表示軸壓比()為0，在極限點時計算的混凝土剪力。由圖11(c)可見：c,uFEA/c,uFEAn0和的關系可表示為c,uFEA/c,uFEAn0= 1+0.35。總結約束效應系數(p)、高寬比()和軸壓比()的影響，c,u1的表達式為

(a)s,uFEA/s,f?p；(b)s,uFEA/s,uFEA1.16?；(c)s,uFEA/s,uFEAn0?

圖10s,uFEA/s,f?p，s,uFEA/s,uFEA1.16?和s,uFEA/s,uFEAn0?關系

Fig. 10 Relations ofs,uFEA/s,f?p，s,uFEA/s,uFEA1.16?ands,uFEA/s,uFEAn0?

(a) Vc,uFEA/Vc,f ?ξp；(b) Vc,uFEA /Vc,uFEA1.16?h/B；(c) Vc,uFEA/Vc,uFEAn0?n

c,c為圓柱體抗壓強度，N/mm2。總結核心混凝土平面抗剪承載力(c,u1)和斜壓桿抗剪承載力(c,u2)可以得到混凝土抗剪極限承載力(c,u)為

因此，根據疊加原理方鋼管混凝土柱?鋼梁外環板式節點核心區抗剪極限承載力(u)為

3.1.3 抗剪屈服承載力(y)

根據計算結果和試驗結果可知：核心區的抗剪屈服承載力(y)和抗剪極限承載力(u)關系為

y=0.68u(12)

假設鋼管與核心混凝土變形協調，核心區節點域的變形圖如圖12所示。圖中：c和t分別為平面壓縮應變和平面拉伸應變；ε和ε分別為向和向應變；γ為剪切應變；為核心區對角線和水平面的夾角。c，t和γ計算表達式分別為：

設tc=?t/c，聯立方程組可得剪切應變(γ)為

當混凝土的壓縮應變(c)取核心混凝土峰值壓應變值(0)[18]見式(14)，可得到核心區極限剪切變形(u)見式(15)。

圖12 節點域變形狀態

為了確定u，首先得求出tc。本文研究tc與約束效應系數(p)，uu,1.16與高寬比()及uu,n0與軸壓比()的關系分別如圖13(a)~(c)所示。由圖13(a)可見：tc與p成比例關系，tc=1.7。由圖13(b)可見：uu,1.16與成線性關系，uu,1.16=0.837+0.05。由圖13(c)可見：uu,n0與呈線性關系，uu,n0=1?0.1。因此，極限剪切變形(u)為

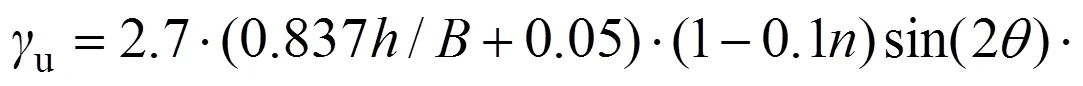
本文所提公式的應用范圍如下：y,p為393~526 N/mm2，c,p為22~49 N/mm2，為6~12 mm，p為1.5~3.4，為0~0.8，為0.7~2.0。

(a) ktc?ξp；(b) γu/γu,1.16?h/B；(c) γu/γu,n0?n

方鋼管混凝土柱?鋼梁節點剪力?剪切變形曲線的恢復力模型可選用平頂退化三線型模型如圖14所示，其骨架線可按圖8確定，彈性階段按彈性剛度加、卸載，彈塑性階段按骨架線進行加載。如從1點或3點卸載時，卸載軌跡可近似取斜直線，按彈性剛度進行卸載。卸載至反向2點或4點再加載，2點或4點縱坐標為1點和3點的0.3倍。再加載線為斜直線，目標點為上一循環的卸載點。若為第1次反向加載，則目標點為骨架線上的屈服點。

圖14 核心區剪力?剪變恢復力模型

3.2 恢復力模型的驗證

為驗證本文提出帶樓板的方鋼管混凝土柱?鋼梁外環板式節點核心區剪力?剪切變形恢復力模型的合理性，將試驗結果和有限元模擬結果與其進行對比，結果見圖15。由圖15可見：忽略有限元模擬結果中由損傷導致的節點剛度退化外，恢復力模型的彈性階段剛度、承載力等與模擬結果和試驗結果吻合較好。

圖15 CFRTJ-4核心區剪力?剪切變形模型、有限元計算結果和試驗結果的比較

4 結論

1) 考慮材料非線性、混凝土的損傷退化、鋼管和核心混凝土間的接觸等因素，建立了帶樓板的鋼管混凝土柱?鋼梁外環板式節點精細有限元模型。

2) 獲得了柱寬厚比、核心混凝土強度、柱軸壓比以及節點核心區高寬比等參數對節點抗剪承載力的影響規律，提出節點抗剪承載力計算公式。

3) 提出考慮樓板影響的方鋼管混凝土柱?鋼梁外環板式節點的核心區剪力?剪切變形恢復力模型。

[1] 李志南. 帶樓板鋼管混凝土環梁節點的試驗研究和有限元分析[D]. 長沙: 中南大學土木工程學院, 2008: 1?79. LI Zhinan. Finite element analysis and experimental research of CFST connections with exterior diaphragms considering floor slab[D]. Changsha: Central South University. School of Civil Engineering, 2008: 1?79.

[2] 別雪夢, 李召, 管文強, 等. 帶樓板的外加強環式 CFST 節點非線性數值模擬[J]. 工業建筑, 2016, 46(10): 163?168. BIE Xuemeng, LI Zhao, GUAN Wenqiang, et al. Nonlinear numerical simulation on the behavior of CFST connections with exterior diaphragms considering floor slab[J]. Industrial Construction, 2016, 46(10): 163?168.

[3] 王文達, 秦庚, 張鵬鵬. 鋼管混凝土柱?鋼梁外環板節點抗彎承載力計算方法[J]. 土木建筑與環境工程, 2011, 33(4): 29?34. WANG Wenda, QIN Geng, ZHANG Pengpeng. Design approach on flexural load-carrying capacity of steel beam to CFST column joints with external stiffening ring[J]. Journal of Civil, Architectural and Environmental Engineering, 2011, 33(4): 29?34.

[4] 黃炳生, 杜培源, 黃顧忠. 方鋼管混凝土柱?鋼梁外隔板節點擬靜力試驗研究[J]. 土木工程學報, 2012, 45(5): 50?57. HUANG Bingsheng, DU Peiyuan, HUANG Guzhong. Quasi-static experimental study of outer diaphragm connections between square concrete filled steel tube columns and steel beams[J]. China Civil Engineering Journal, 2012, 45(5): 50?57.

[5] LI X, XIAO Y, WU Y T. Seismic behavior of exterior connections with steel beams bolted to CFT columns[J]. Journal of Constructional Steel Research, 2009, 65(7): 1438?1446.

[6] QUAN C, WANG W, ZHOU J, et al. Cyclic behavior of stiffened joints between concrete-filled steel tubular column and steel beam with narrow outer diaphragm and partial joint penetration welds[J]. Frontiers of Structural and Civil Engineering, 2016, 10(3): 333?344.

[7] 聶建國, 秦凱, 肖巖. 方鋼管混凝土柱節點的試驗研究及非線性有限元分析[J]. 工程力學, 2006, 23(11): 99?115. NIE Jianguo, QIN kai, XIAO Yan. Experimental investigation and nonlinear finite element analysis on the behavior of concrete-filled square steel tubular column connections[J]. Engineering Mechanics, 2006, 23(11): 99?115.

[8] 劉威. 鋼管混凝土局部受壓時的工作機理研究[D]. 福州: 福州大學土木工程學院, 2005: 1?158. LIU Wei. Research on mechanism of concrete-filled steel tubes subjected to local compression[D]. Fuzhou: Fuzhou University. College of Civil Engineering, 2005: 1?158.

[9] 過鎮海. 鋼筋混凝土原理[M]. 北京: 清華大學出版社, 2013: 1?22. GUO Zhenhai. Principles of reinforced concrete[M]. Beijing: Tsinghua University Press, 2013: 1?22.

[10] ACI Committee 318. Building code requirements for structural concrete and commentary[M]. Detroit, USA: American Concrete Institute, 2014: 1?5.

[11] GB 50010—2010, 混凝土結構設計規范[S]. GB 50010—2010, Code for Design of Concrete Structures[S].

[12] ABAQUS Inc. ABAQUS analysis theory manual[M]. Rhale Island: ABAQUS Inc, 2016: 1?841.

[13] NISHIYAMA I, FUJIMOTO T, FUKUMOTO T, et al. Inelastic force-deformation response of joint shear panels in beam-column moment connections to concrete-filled tubes[J]. Journal of Structural Engineering, 2004, 130(2): 244?252.

[14] CHENG C T, CHUNG L L. Seismic performance of steel beams to concrete-filled steel tubular column connections[J]. Journal of Constructional Steel Research, 2003, 59(3): 405?426.

[15] FUKUMOTO T, MORITA K. Elastoplastic behavior of panel zone in steel beam-to-concrete filled steel tube column moment connections[J]. Journal of Structural Engineering, ASCE, 2005, 131(12): 1841?1853.

[16] 李威. 圓鋼管混凝土柱?鋼梁外環板式框架節點抗震性能研究[D]. 北京: 清華大學土木工程系, 2011: 1?159. LI Wei. Study on the seismic performance of circular concrete- filled steel tubular column to steel beam joint with external diaphragm[D]. Beijing: Tsinghua University. Department of Civil Engineering, 2011: 1?159.

[17] 秦凱. 方鋼管混凝土柱與鋼?混凝土組合梁連接節點的性能研究[D]. 北京: 清華大學土木工程系, 2006: 1?158. QIN Kai. Study on the performance of concrete filled square steel tubular column-steel concrete composite beam[D]. Beijing: Tsinghua University. Department of Civil Engineering, 2006: 1?158.

[18] 韓林海. 鋼管混凝土結構-理論與實踐[M]. 2版. 北京: 科學出版社, 2007: 1?755. HAN Linhai. Concrete filled steel tube structure- theory and practice[M]. 2nd ed. Beijing: Science Press, 2007: 1?755.

[19] GB 50017—2003, 鋼結構設計規范[S]. GB 50017—2003, Code for design of steel structures[S].

[20] 唐九如. 鋼筋混凝土框架節點抗震[M]. 南京: 東南大學出版社, 1989: 1?544. TANG Jiuru. Seismic resistance of joints in reinforced concrete frames[M]. Nanjing: Southeast University Press, 1989: 1?544.

[21] PARRA-MONTESINOS G, WIGHT J K. Modeling shear behavior of hybrid RCS beam-column connections[J]. Journal of Structural Engineering, 2001, 127(1): 3?11.

(編輯 楊幼平)

Shear performance of square concrete-filled steel tubular column to steel beam joint with external diaphragm

BIE Xuemeng, LI Zhao, GUAN Wenqiang, DU Guofeng

(1. School of Urban Construction, Yangtze University, Jingzhou 434023, China; 2. Structural Engineering and Disaster Prevention Research Institute, Yangtze University, Jingzhou 434023, China)

Detailed finite element analysis (FEA) model was established to investigate the shear performance of square concrete-filled steel tubular (CFST) column to steel beam joint with external diaphragm under seismic loading on the basis of the size of the joint in test. The material non-linearity, the damage degradation of concrete under cyclic loading and the interaction between steel and concrete were considered in this model. Experimental result was compared to validate the feasibility of this model in simulating the behavior of the composite joints in cyclic loading. Simultaneously, parametric studies were carried out to study the influence of the following parameters on the shearing capacity and deformation in panel zone: ratio of width to thickness of column, the concrete strength of panel zone, the axial load ratio of the column and the ratio of depth to width of panel zone. Eventually, a shear force-deformation restoring-force model of panel zone in composite joints was proposed. The results show that the restoring-force model is practical and can provide practical basis for engineering design.

concrete filled steel tubular (CFST) column-steel beam joint with external diaphragm; finite element analysis (FEA); reinforced concrete (RC) slab; shear performance

TU317.1

A

1672?7207(2018)01?0226?12

10.11817/j.issn.1672-7207.2018.01.029

2017?01?01；

2017?03?20

國家自然科學基金資助項目(51778064, 51378077)；湖北省自然科學基金(創新群體)資助項目(2015CFA029, 2016CFA022)；中國石油科技創新基金資助項目(2016D-5007-0605) (Projects(51778064, 51378077) supported by the National Natural Science Foundation of China; Projects (2015CFA029, 2016CFA022) supported by the Natural Science Foundation of Hubei Province (Innovation Group); Project (2016D-5007-0605) supported by Petroleum Science and Technology Innovation Foundation of China)

杜國鋒，博士，教授，碩士生導師，從事智能材料與結構、工程結構抗震研究；E-mail: gfd_1125@126.com