復雜軸線拱結構實用解析解研究

胡常福，何兵兵，石萃佳，任偉新

?

復雜軸線拱結構實用解析解研究

胡常福1，何兵兵1，石萃佳1，任偉新2

(1. 華東交通大學土木建筑學院，江西南昌，330013；2. 合肥工業大學土木與水利工程學院，安徽合肥，230009)

拱結構力學問題的解析解大多基于沿拱軸的曲線積分，當拱軸線為非圓弧線時該曲線積分往往沒有閉合解析解。針對該問題，提出近似曲線積分方法，將精確弧長微分近似顯示表達，用以得到拱結構力學問題的實用解析解。基于本文方法，以包含大量復雜曲線積分的新型拱軸線彈性常數表達式及主拱圈自重、橋面系自重作用時內力表達式為研究對象，推演得到其實用解析解，并以彈性常數精確曲線積分的數值解與內力的有限元解為精確解，驗證本文方法的高精確性與實用性。研究結果表明：與常規方法將曲線積分簡化為直線積分相比，本文方法能得到更高精度的實用解析解，各彈性常數表達式最大相對誤差小于2%；與內力的有限元解相比，本文方法具有更通用的實用表達式，且內力的最大相對誤差小于4%。

拱結構；實用解析解；弧長微分；近似曲線積分

拱結構是基本的橋梁結構型式之一，因力學性能優異，在國內外廣泛使用[1]。在拱結構力學問題的解析解研究中，大多數使用了基于能量原理的方法，如彈性常數、內力分析、連拱問題中的虛功原理[2]，變形分析中的虛位移原理[3]、分枝點穩定[4]、躍越屈曲[5]與動力屈曲[6]中使用的能量方法以及自振分析中的能量守恒原理[7]等。在拱結構中應用這些能量方法時，都需要沿拱軸進行曲線積分。拱結構力學問題是否有解析解，建立在該曲線積分是否有顯示解析解的基礎之上。對于不同的拱軸線，求解曲線積分顯示解析解的方法也各不相同。在圓弧拱中，由于曲率處處相等，弧長微分得以簡化，沿拱軸的曲線積分就簡化為以圓心角為變量的普通直線積分，因此，圓弧拱的各種力學問題均得到了顯示解析解[2, 4, 6?8]。然而，圓弧線對應于等深度靜水壓力，與實際拱橋荷載型式相差較大，在實際拱橋工程中應用并不多。相反的是，使用最頻繁的如拋物線、懸鏈線等非圓弧拱軸線，沿拱軸的曲線積分反而沒有解析解。為解決這個問題，KOOLEE等[9]在拋物線拱的自振分析中，將直角坐標系下的拋物線弧長微分，轉換為極坐標系下進行表達，希望達到像圓弧拱那樣簡便的普通直線積分，但最終仍采用了數值積分得出結果；WANG等[10]針對英國石拱橋承載力評估方法MEXE中的沿拋物線拱軸的曲線積分，將弧長微分簡化為直線微分，進而使得沿拋物線拱軸的曲線積分簡化為沿水平坐標軸的直線積分，雖得到了顯示解，但在矢跨比較大的陡拱中誤差增大[11]；BRADFORD等[3]在拋物線淺拱穩定問題中，將沿拋物線拱軸的曲線積分簡化為沿水平坐標軸的直線積分，得到的結果僅適用于矢跨比較小的淺拱，其驗證的算例矢跨比均小于1/10、驗證的試驗拱[12]矢跨比為1/18.8與1/25。YI等[13]在含有彈性支撐淺拱的振動分析中，采用了將曲線積分簡化為直線積分的方法；MOON等[14]在拋物線淺拱的屈曲分析中，將沿拱軸的曲線積分簡化為沿水平坐標軸的直線積分；我國拱橋手冊[2]中，采用數值積分方法計算沿拱軸的曲線積分，并通過對結果進行列表，來解決沿拱軸曲線積分無法顯示表達問題；胡常福等根據懸索線[15]弧長微分可顯示表達的特點，得到了拋物線[16]、懸鏈線[17]拱軸曲線積分的實用解析解。由此可以看出：針對沿非圓弧拱軸曲線積分無法顯示表達的問題，使用最廣泛的方法是將其簡化為沿水平坐標軸的直線積分，該方法雖簡便但僅適用于淺拱，在陡拱中存在較大誤差，求解沿非圓弧拱軸曲線積分的高精度顯示解仍非常困難。針對該問題，本文作者提出近似曲線積分方法，將精確弧長微分近似顯示化用以得到曲線積分的實用解析解，以沿新型復雜拱軸線[18]的曲線積分為研究對象，以包含大量曲線積分的彈性常數及主拱圈自重、橋面系自重作用下內力為研究內容，基于所提出的方法推演其實用解析解，并通過數值積分與有限元法結果，驗證本文方法高精度性與顯示表達式的特點。

1 復雜軸線精確弧長微分的顯式近似

任偉新等[18]針對下承空腹式拱橋恒載的主要分布型式為橋面系自重與主拱圈自重，提出了一個新型的復雜拱軸線，如下式所示：

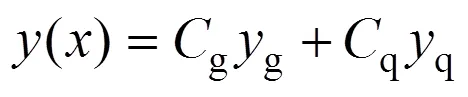
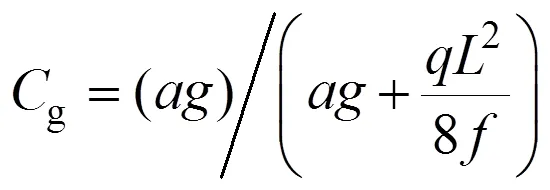
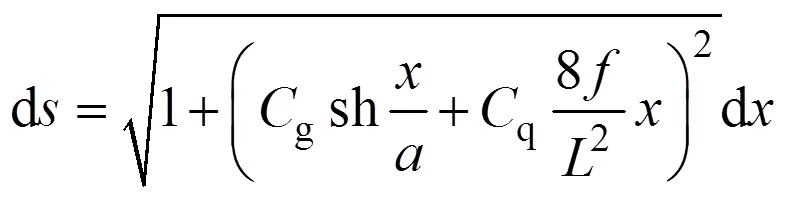
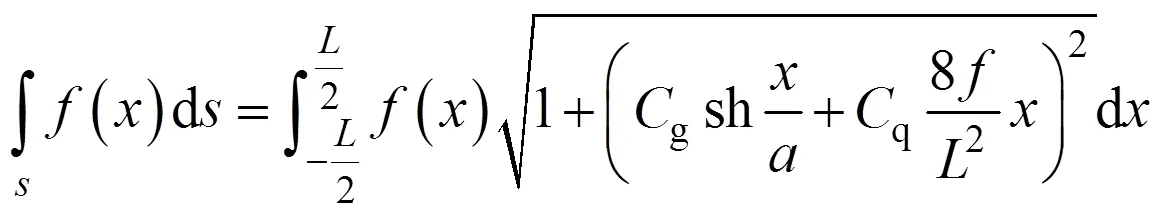
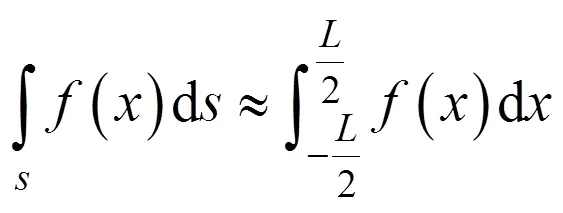
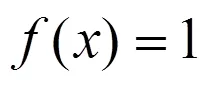
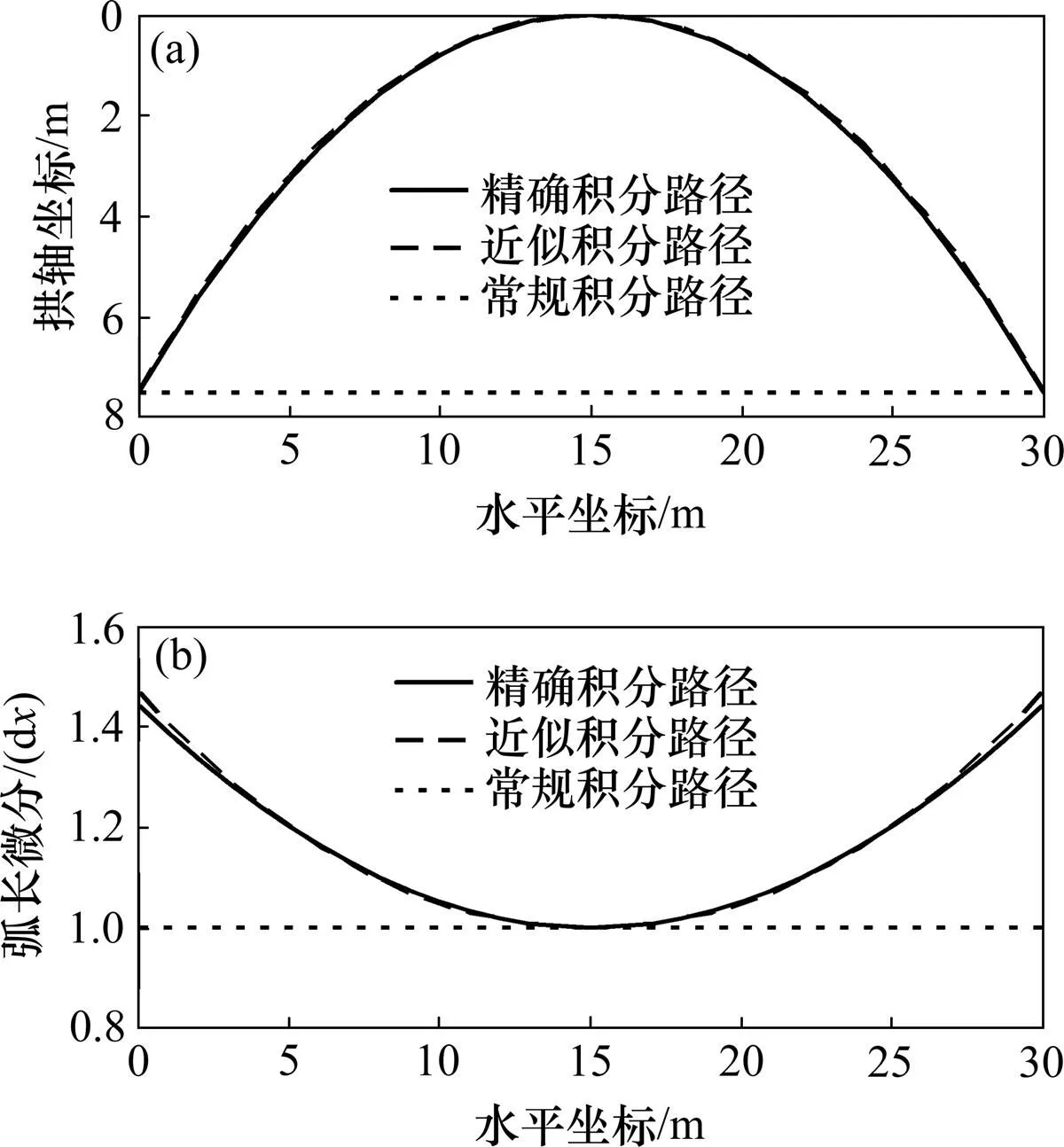
(a) 3種方法積分路徑比較；(b) 3種方法弧長微分比較

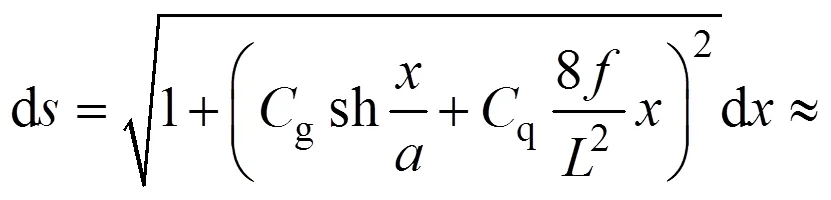
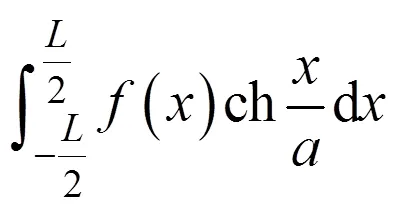
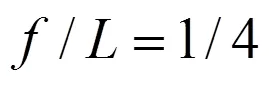
在拱結構所有的力學問題的解析解中，彈性常數及內力分析包含的沿拱軸曲線積分數量最多。為此，以無鉸拱、兩鉸拱的彈性常數表達式及橋面系自重、主拱圈自重作用下內力表達式為研究對象，展現近似曲線積分方法所具有的高精度顯示解析解特點，進一步驗證本文方法的有效性。

2 復雜軸線拱的彈性常數及內力實用解析解

2.1 彈性常數實用解析解

基于如式(5)所示的近似曲線積分方法，即可推演組合線兩鉸拱常變位彈性常數的實用解析解，如下式所示：

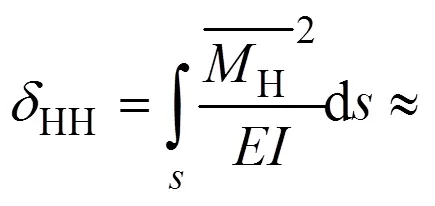
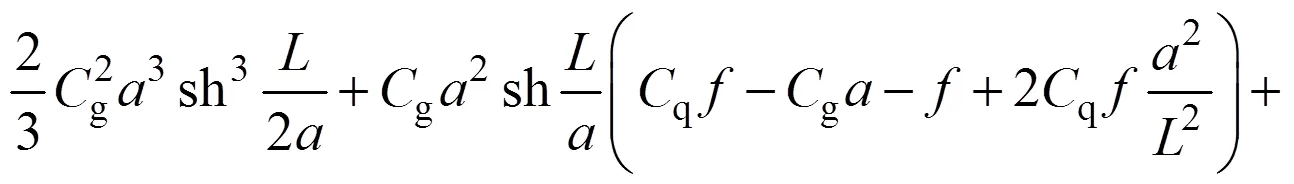
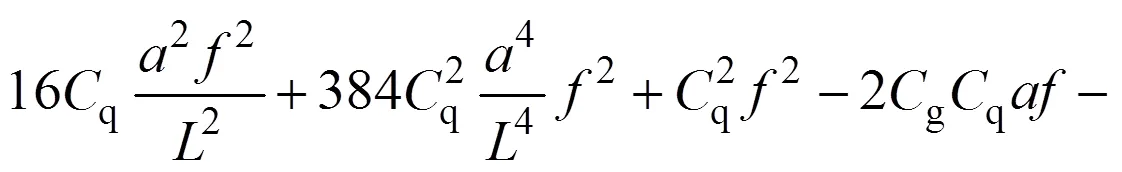
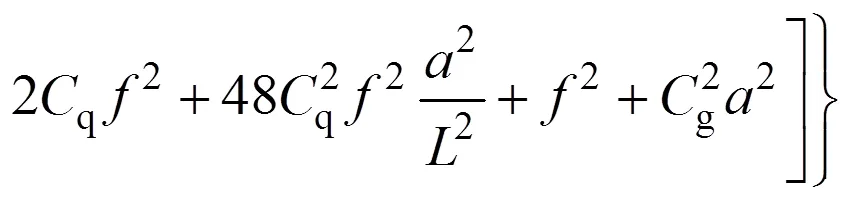
2.2 內力實用解析解

基于如式(5)所示的近似曲線積分方法，即可推演主拱圈自重作用下組合線兩鉸拱載變位的實用表達式，如下式所示：

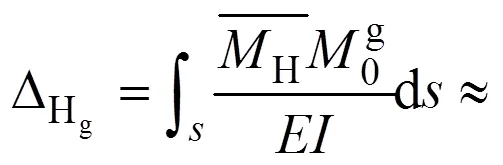
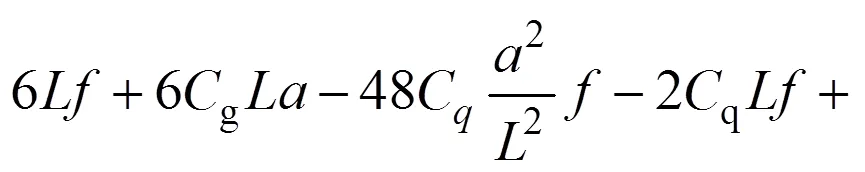
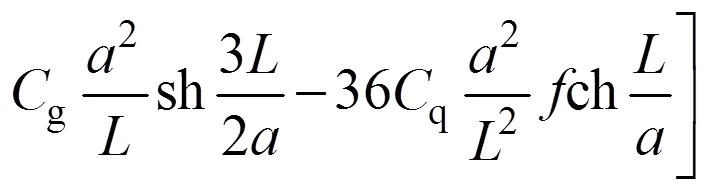
表1 彈性常數實用解析解

綜合表1與表2，即可求得兩鉸拱、無鉸拱結構體系在主拱圈自重、橋面系自重荷載作用下的內力實用表達式，如表3所示。

表2 載變位實用解析解

表3 內力的實用解析解

3 精度分析與算例驗證

在以上的分析中，基于近似曲線積分方法，針對彈性常數與內力分析中所包含大量的復雜曲線積分，均得到了實用的解析解，表明本文方法在求解復雜拱軸曲線積分顯示解方面的有效性。下面以彈性常數的數值積分解與內力的有限元解為精確解，來驗證本文方法結果的高精度性。

3.1 彈性常數精度分析

為驗證本文方法彈性常數實用解析解的精度，分別使用精確曲線積分數值積分方法、本文近似曲線積分方法與簡化為水平直線積分的常規方法，來計算表1中各彈性常數在/=1時的數值，并以精確曲線積分的數值積分結果為精確解，比較本文方法與常規方法的精度，如表4所示。

由表2可以看出：隨著矢跨比由1/3變化至1/10，各彈性常數中本文方法與常規方法的相對誤差都減小，本文方法相對誤差明顯比常規方法的小；當矢跨比為1/10時，常規方法計算的各彈性常數最大相對誤差為5.239 5%，最小相對誤差為1.113 5%。而在同樣的矢跨比中本文方法最大相對誤差為0.029 1%，最小相對誤差為0.004 8%，明顯比常規方法更優；當矢跨比為1/3時，常規方法計算的各彈性常數最大相對誤差為51.527 9%，最小相對誤差為7.740 0%，表明在陡拱中常規方法已經不能使用，而在同樣的矢跨比中本文方法最大相對誤差為1.155 4%，最小相對誤差為 0.239 5%，顯示了本文方法具有相當高的精度。

表5 3種方法彈性常數相對誤差比較

綜合表1與表2可知：在各彈性常數的計算結果中，常規方法在陡拱中誤差較大，而本文方法在陡拱與淺拱中均具有較高的精度，各彈性常數最大相對誤差小于2%。

3.2 內力表達式算例驗證

某跨徑255 m的拱橋[19]，矢跨比為1/4，拱肋面積為0.77 m2，慣性矩為0.775 m4，彈性模量為201 GPa，材料容重為78.5 kN/m3，橋面系平均重力為 1 208.9 kN/m，拱軸線為如式(1)所示的復雜拱軸線型。為驗證本文方法內力實用表達式結果的精確性，分別使用有限元法及本文方法計算兩鉸拱與無鉸拱2個結構體系，在主拱圈自重作用、橋面系自重作用時的結構內力，兩者結果的比較如圖2所示。

由圖2可以看出：在主拱圈自重、橋面系自重2種荷載作用工況下，兩鉸拱、無鉸拱兩種結構體系的彎矩與軸力中，本文方法的計算結果與有限元結果均吻合較好。通過對內力的精度計算，本文方法軸力最大相對誤差為3.62%，彎矩最大相對誤差為3.30%，顯示了本文方法具有較好的精度。同時，由彈性常數精度分析結果可知，本文方法在矢跨比大時誤差會增加，而本算例矢跨比為1/4，已是實際拱橋的最大矢跨比。由此可知，本文方法在各種矢跨比情況下均與有限元結果吻合較好，且能保持較高的精度。

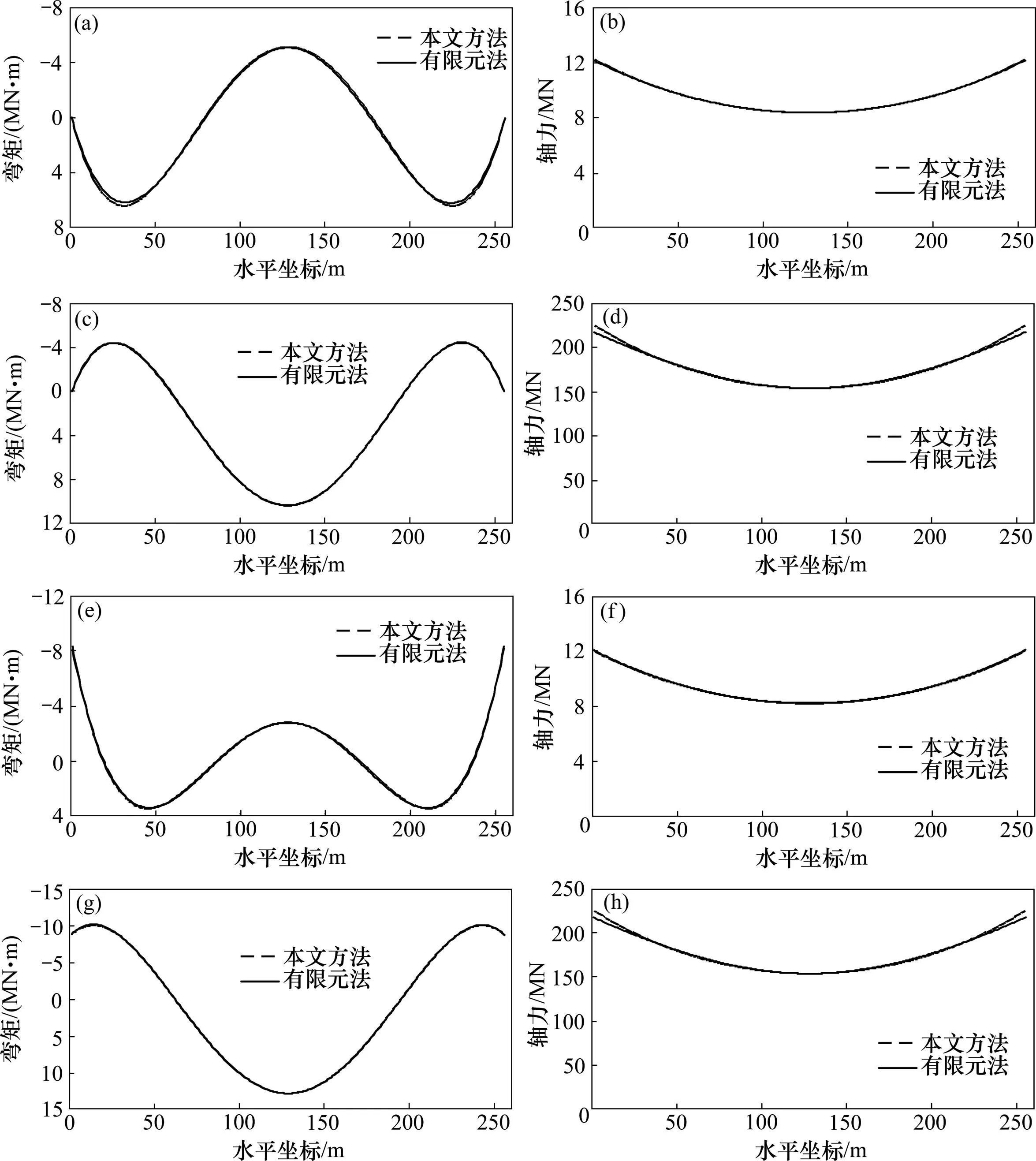
(a) 兩鉸拱主拱圈自重工況彎矩比較；(b) 兩鉸拱主拱圈自重工況軸力比較；(c) 兩鉸拱橋面系自重工況彎矩比較；(d) 兩鉸拱橋面系自重工況軸力比較；(e) 無鉸拱主拱圈自重工況彎矩比較；(f) 無鉸拱主拱圈自重工況軸力比較；(g) 無鉸拱橋面系自重工況彎矩比較；(h) 無鉸拱橋面系自重工況軸力比較

4 結論

1) 通過概念分析、公式推演與精度分析可知，近似曲線積分方法可以用于求解復雜拱軸曲線積分的高精度實用解析解。

2) 基于近似曲線積分方法能得到復雜拱軸線下彈性常數的實用解析解，公式簡潔且在陡拱下也保持了非常高的精度，各彈性常數最大相對誤差不超過2%。

3) 基于近似曲線積分方法能得到復雜拱軸線下的內力實用解析解，公式簡潔且與有限元解吻合較好，內力最大相對誤差不超過4%。

[1] XU Zhen, LU Xinzheng, GUAN Hong, et al. Progressive- collapse simulation and critical region identification of a stone arch bridge[J]. Journal of Performance of Constructed Facilities, ASCE, 2013, 27(1): 43?52.

[2] 顧懋清, 石紹甫. 公路橋涵設計手冊(拱橋上)[M]. 北京: 人民交通出版社, 1994: 522?1175. GU Maoqing, SHI Shaofu. Manual of highway bridge and culvert (arch bridge, volumeⅠ)[M]. Beijing: China Transportation Publishing House, 1994: 522?1175.

[3] BRADFORD M A, WANG T, PI Y L, et al. In-plane stability of parabolic arches with horizontal spring supports. Ⅰ: Theory [J]. Journal of Structural Engineering, ASCE, 2014, 133(8): 1130?1137.

[4] PI Y L, BRADFORD M A, UY B. In-plane stability of arches[J]. International Journal of Solids & Structures, 2002, 39(1): 105?125.

[5] CAI Jianguo, XU Yixiang, FENG Jian, et al. In-plane elastic buckling of shallow parabolic arches under an external load and temperature changes[J]. Journal of Structural Engineering, ASCE, 2014, 138(11): 1300?1309.

[6] PI Y L, BRADFORD M A. Multiple unstable equilibrium branches and non-linear dynamic buckling of shallow arches[J]. International Journal of Non-Linear Mechanics, 2014, 60: 33?45.

[7] ZHAO Yueyu, KANG Houjun. In-plane free vibration analysis of cable-arch structure[J]. Journal of Sound & Vibration, 2008, 312(3): 363?379.

[8] GUO Yanlin, ZHAO Siyuan, DOU Chao, et al. Out-of-plane elastic buckling of circular arches with elastic end restraints[J]. Journal of Structural Engineering, ASCE, 2014, 140(10): 890?914.

[9] KOOLEE B, SANG J, GUANG Fanli, et al. Free vibration analysis of parabolic arches in cartesian coordinates[J]. International Journal of Structural Stability & Dynamics, 2011, 3(3): 337?390.

[10] WANG J, MELBOURNE C. Mechanics of MEXE method for masonry arch bridge assessment[J]. Journal of the ICE- Engineering and Computational Mechanics, 2010, 163(3): 187?202.

[11] 胡常福, 任偉新, 尚繼宗. 基于近似曲線積分的MEXE修正方法改進研究[J]. 湘潭大學自然科學學報, 2013, 35(1): 63?66. HU Changfu, REN Weixin, SHANG Jizong. Development of modified MEXE method based on approximate curve integral method[J]. Natural Science Journal of Xiangtan University, 2013, 35(1): 63?66.

[12] WANG T, BRADFORD M A, GILBERT R, et al. In-plane stability of parabolic arches with horizontal spring supports, Ⅱ: Experiments[J]. Journal of Structural Engineering, ASCE, 2007, 133(8): 1138?1145.

[13] YI Zhuangpeng, WANG Lianhua, KANG Houjun, et al. Modal interaction activations and nonlinear dynamic response of shallow arch with both ends vertically elastically constrained for two-to-one internal resonance[J]. Journal of Sound & Vibration, 2014, 333(21): 5511?5524.

[14] MOON J, YOON K Y, LEE T H, et al. In-plane elastic buckling of pin-ended shallow parabolic arches[J]. Engineering Structures, 2007, 29(10): 2611?2617.

[15] HU Changfu, WAN Yi, SHANGGUAN Xing. A new practice in the design of arch axis[C]// Proceedings of 6th International Conference on Arch Bridge, Fuzhou, China, 2010: 709?715.

[16] 胡常福, 雷亮亮, 陳海龍, 等. 等截面拋物線拱橋內力實用解析解研究[J]. 鐵道科學與工程學報, 2011, 8(5): 97?103.HU Changfu, LEI Liangliang, CHEN Hailong, et al. Research on practical analytic solution of parabolic arch bridges with uniform section[J]. Journal of Railway Science and Engineering, 2011, 8(5): 97?103.

[17] 胡常福, 陸小雨, 甘慧慧, 等. 基于近似積分的懸鏈線拱實用解析解[J]. 中南大學學報(自然科學版), 2015, 46(3): 1058?1065.HU Changfu, LU Xiaoyu, GAN Huihui, et al. Practical analytical solution of catenary arch based on approximate integration method[J]. Journal of Central South University (Science and Technology), 2015, 46(3): 1058?1065.

[18] 任偉新, 胡常福, 上官興. 等. 空腹式拱橋新型拱軸線研究[J]. 交通科學與工程, 2010, 26(2): 26?30. REN Weixin, HU Changfu, SHANGGUAN Xing, et al. Research on new arch axis of open-spandrel arch bridge[J]. Journal of Transport Science and Engineering, 2010, 26(2): 26?30.

[19] PAN Yang, HU Changfu, WU Tongao, et al. A new deck-type CFST arch bridge with diagonal web cables[C]// The 3rd Chinese- Croatian Joint Colloquium on Long Span Arch Bridge. Zagreb, Croatia, 2011: 133?140.

(編輯 楊幼平)

Research on approximate analytical solution of arch structure with complex arch axis

HU Changfu1, HE Bingbing1, SHI Cuijia1, REN Weixin2

(1. School of Civil Engineering and Architecture, East China Jiaotong University, Nanchang 330013, China; 2. School of Civil Engineering and Water Conservancy, Hefei University of Technology, Hefei 230009, China)

The curve integration along arch axis is a basic problem of analytical solution method in arch structure mechanics, and it has no closed form analytical solution when the arch axis is not an arc. An approximate curve integration method was proposed to solve this problem. It took approximate display arc-length differentiation to replace the complex exact one to obtain the practical closed form analytical solution of arch structure mechanics problem. Based on the proposed method, some practical analytical solutions were deduced, by studying arch structure elastic constant and main arch ring inner force under main arch ring and deck system dead load in a new complex axis arch structure, since it had a lot of complex curve integrations along arch axis in these mechanics problems. Numerical integration solution of elastic constant using exact arc-length differentiation and finite element solution of inner force were taken as exact solutions to verify high precision of the display result of proposed method. The results show that compared with the normal method which takes curve integration simplified to horizontal line integration, the proposed method can get higher precision approximate expression results, and the maximum relative error of all elastic constants is less than 2%; compared with finite element solution, the proposed method have more general approximate expression, and the maximum relative error of all inner force is less than 4%.

arch structure; approximate analytical solution; arc-length differentiation; approximate curve integration

U441

A

1672?7207(2018)01?0217?09

10.11817/j.issn.1672-7207.2018.01.028

2017?01?09；

2017?03?16

國家自然科學基金資助項目(51568020)；國家留學基金資助項目(201608360147)；江西省科技支撐計劃項目(20141BBG70089) (Project(51568020) supported by the National Natural Science Foundation of China; Project(201608360147) supported by China Scholarship Council; Project(20141BBG70089) supported by Science and Technology Plan in Jiangxi Province)

胡常福，博士，講師，從事拱結構力學研究；E-mail: hcf@ecjtu.jx.cn