基于電力系統主導振蕩模式提取的區域負荷模型識別研究

郝麗麗， 汪成根， 方 鑫， 談怡君， 侯佳欣， 熊海波

(1. 南京工業大學電氣工程與控制科學學院，江蘇 南京 211816；2. 國網江蘇省電力有限公司電力科學研究院，江蘇 南京 211103；3. 國網豐縣供電公司，江蘇 豐縣 221700)

0 引言

電力系統多次發生仿真結果無法復現事故真實情況的事件[1-5]，仿真的有效性問題亟待解決。模型的不準確是導致仿真結果異于系統實際運行狀況的關鍵因素之一。通過信息采集和狀態估計，可獲得較為準確的電力系統網絡拓撲模型。系統額定運行狀態下，線路、變壓器、電容、電抗器等元件的模型參數較為準確，通過廠家測試、獨立建模與定期跟蹤檢驗，發電機及其控制器的模型也較為可靠。然而，作為電力系統重要元件之一的負荷，在發輸電網中其模型通常是由負荷、變壓器、電源、儲能、補償設備等值得到。系統中負荷數目繁多、接入分散，且負荷具有隨機性和時變性，所以負荷很難逐一、準確建模，負荷模型較系統的其它元件更加不可信，是仿真誤差的主要來源之一[6-8]。

將特征接近的空間負荷點歸為一類，統一辨識各類負荷的方法兼顧了模型的準確性和計算效率[9-11]。負荷分類涉及負荷特征向量的選取與聚類，選取的樣本特征應能完全體現樣本的本質[12-14]，且不影響識別結果的強壯性[15-16]。需要基于不同的聚類原則與實際需要選擇合適的聚類方法[17-20]。此外，針對負荷的時變性，仿真系統中的負荷模型應能跟蹤負荷實際變化，如何兼顧負荷的時間、空間分布規律，根據現場測量信息及時識別并自動更新負荷模型，建立更為準確的自適應負荷模型，是探討的重點。

通過分析系統主導振蕩模式選取觀測母線，制定模型識別的目標函數，以負荷用電性質構成比例作為負荷節點的特征，對空間負荷進行分類，同類負荷采用相同的模型參數，用梯度優化算法對系統各類負荷進行統一識別。文中分別在IEEE 39和118節點系統上進行驗證，結果表明以負荷用電性質構成比例進行分類，得到的負荷識別結果強壯性更好，同時展示了負荷時變分類閾值的選取方法。

1 基于負荷用電性質構成比例的負荷分類

1.1 分類特征的選取

就用電性質而言，負荷一般可分為工業、商業、農業、居民負荷及其他4類。各類負荷的特征一般比較固定，如商業負荷、居民及其他負荷包含比重較大的靜態用電設備，而工業負荷中電動機負荷比重較大，農業負荷多為灌溉負荷。統計表明，各種性質負荷的恒阻抗負荷比例Ap，Aq，恒電流負荷比例Bp，Bq，恒功率負荷比例Cp，Cq和電動機負荷比例Kpm，Kqm具有較為固定的分布規律[21]。因此，可以根據各節點不同用電性質負荷構成比例得到近似的負荷模型參數。文中選取以上4種不同用電性質負荷占所接入負荷節點總負荷量的比例作為負荷節點的分類特征。一個樣本周期內第s(s=1, 2,…,Ns)次采樣得到的第i(i=1, 2,…,n)個負荷節點的負荷用電性質構成比例為Xi,s=(xis1,xis2,xis3,xis4)，其中xis1,xis2,xis3,xis4分別表示第i個負荷第s次采樣時工業、商業、農業、居民負荷及其他所占的用電比例。

大規模電力系統數字仿真中，負荷節點可能是多個實際負荷的聚合，也可能是由多個元件聚合等效并折算到中、高壓側母線得到。對于前者，事先詳細分析負荷節點所接每個實際負荷用戶的用電性質，再根據采集到的各負荷用戶的實時接入情況，計算得到該負荷節點的實時負荷用電性質構成比例進行負荷分類；對于后者，則需逐一分析各類元件的性質，將其歸為某類用電性質的負荷，并按照每個元件的電壓等級進行容量折算，再計入各元件的實時接入情況，計算得到等效負荷節點的實時負荷用電性質構成比例。

1.2 基于模糊C均值聚類算法的負荷分類

文中采用模糊C均值聚類算法，依據1.1節中所選負荷特征，用隸屬度函數判斷n個負荷節點的聚類情況，得到系統總的負荷分類數目為C，并求取每類的聚類中心，使得類內加權誤差平方和最小。用[0,1]間的隸屬度μifi來確定第i個負荷特征屬于第fi(fi=1,2,…,C)組聚類的程度，一個負荷點各組的隸屬度總和為1。

(1)

式中：C為聚類數；n為負荷節點數；μifi為隸屬度值。對負荷特征分類，優化C使得類內距離最小，類間距離最大。類內距離是指同類中與其類中心離差的平方和，表達式如下：

(2)

不同類的類間距函數表達式為：

(3)

式中：m為權值，1≤m≤∞；Xi為某次采樣得到的第i個負荷的特征樣本元素；Vfi,Vfj分別為第fi和fj類負荷的聚類中心,fi≠fj，Vfi表示如下：

(4)

基于模糊C均值聚類算法的負荷分類步驟為：

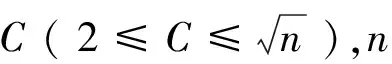
步驟(2)：計算由隸屬度的值所組成的劃分矩陣U；

2 各類負荷節點的統一識別

2.1 觀測母線的選取

選擇能充分、有效反映系統關鍵動態行為的母線作為觀測對象，比較觀測對象上實測與模型仿真響應的差異程度，作為模型識別的目標函數。擾動可能激發系統的多種振蕩模式，與主導振蕩模式相關的母線信息能夠反映模型對系統關鍵動態過程的影響。此外，電壓級別高或關鍵節點變電站，尤其是位于聯絡線上的電站，對系統有更廣泛的影響。如果這些電站仿真響應曲線與測量信息接近，則臨近母線的仿真結果也會與實測接近。因此，在電力系統模型識別中，應選擇那些充分參與系統主導振蕩模式，且位于聯絡線上并具有較高電壓等級的關鍵變電站母線作為觀測對象。基于Prony法從實測信號中提取系統振蕩模式，過程如下。

電力系統是一個高階非線性系統，對于小擾動，我們一般將系統在運行點附近線性化為：

(5)

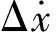
(6)

式中：Ri=ciφiψib，φi和ψi分別為特征根λi的左、右特征向量。當采樣間隔Δt恒定時，yj(t)可以表示為下述離散形式：

(7)

式中：zi=exp(λiΔt)，λi=σi+jω為模型階數；n為未知量；第i個模式的參數zi；Ri可以通過Prony算法估算得到。

方程式(7)可以寫成以下形式：

(8)

式中zi滿足關于未知系數ai的n階多項式的根：

zn-(a1zn-1+a2zn-2+...+anz0)=0

(9)

式(8)兩側左乘[-an,-an-1,...,-a1,1,0,...,0]，可得到：

(10)

式(8)左乘[0,-an,-an-1,...,-a1,1,0,..,0]，等式右側結果也為0。重復式(9)的計算可得下式：

(11)

利用Prony法識別系統振蕩可以同時對所有量測進行頻率、阻尼比、模態的識別，概括為以下步驟：求解式(11)得到系數ai，求解式(7)的根得到zi，求解式(8)中的復數殘差Ri，判別系統的主導振蕩模式及模態,從而確定每個測點參與主導振蕩的程度，進而選擇模型識別的觀測對象。

2.2 模型識別的目標函數

文中選用實際(或參考)系統與仿真(或模型)系統觀測母線的電壓均方誤差作為負荷模型識別的目標函數J表達式為：

(12)

式中：N表示動態響應采樣點數；Vm(j)表示觀測母線的第j個電壓實測值；Vs(j)表示仿真系統中觀測母線的第j個電壓響應。設置誤差閾值εJ，若J>εJ，則表明當前負荷模型無效，需要進行廣域電力系統負荷的空間分類及識別；反之，則表明當前模型有效。

2.3 待識別參數的選取

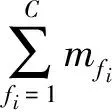
{{α11,α12,...,α1m1},{α21,α22,...,α2m2},...,

{αfi1,αfi2,...,αfimfi},...,{αC1,αC2,...,αCmC}}(13)

目標函數J關于負荷模型參數的靈敏度越大，表明該參數對變量的影響越大，可以優先識別這些靈敏度大的參數；反之，那些靈敏度小的參數，其調整對仿真結果影響微弱，可以用典型值進行替代，從而減少系統待識別參數的個數，減少計算量。

2.4 參數優化算法

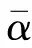
(14)

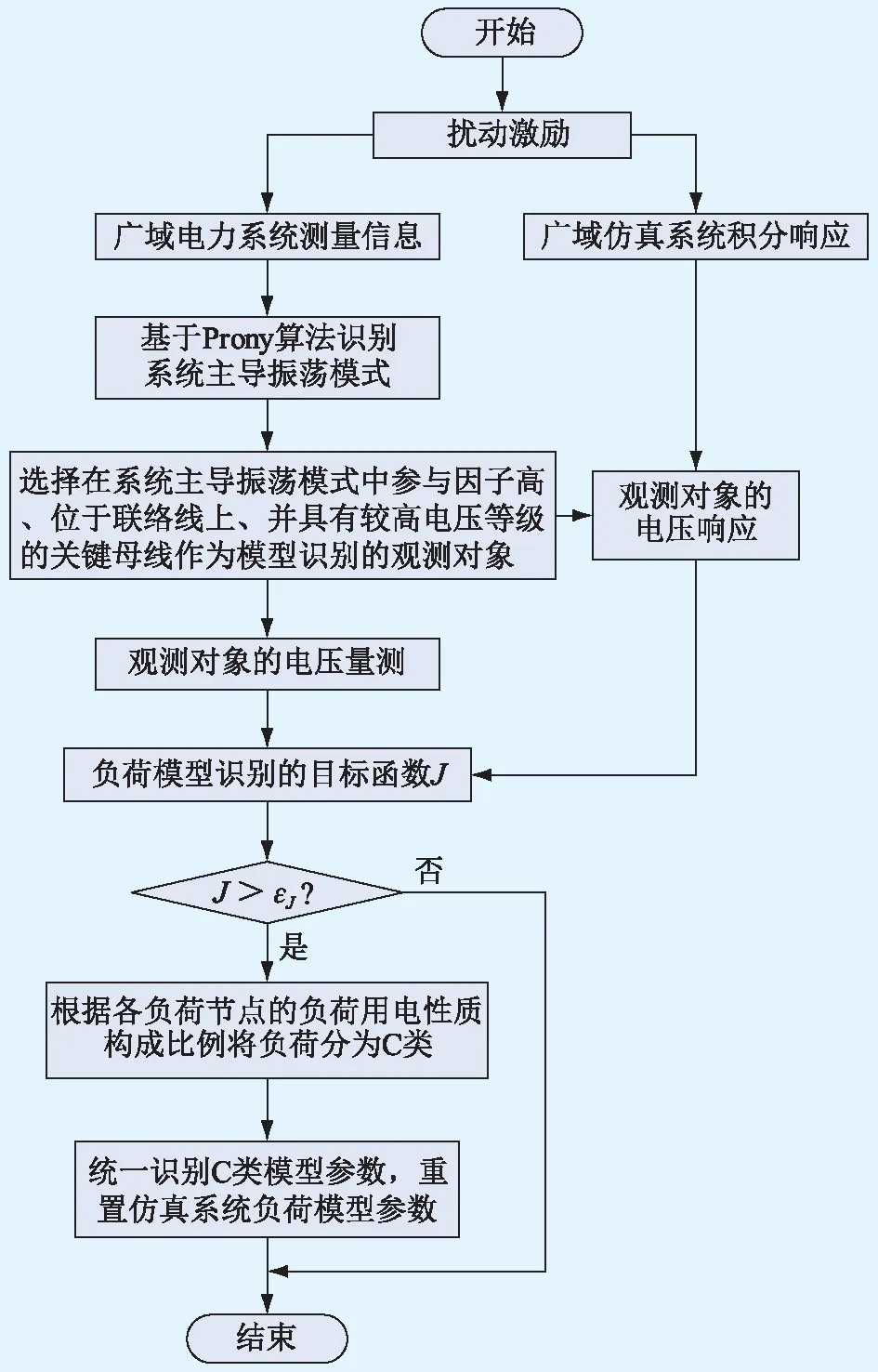
圖1 電力系統負荷的識別模塊流程Fig.1 Identification sub-module of power system load model

3 算例仿真

3.1 IEEE 39節點系統仿真

假設各節點感應電動機內部參數已明確，僅考慮負荷節點上各類靜態負荷和動態負荷占總負荷大小的比例參數，其中Cp=1-Ap-Bp，Cq=1-Aq-Bq。故所需識別的參數為Ap,Aq,Bp,Bq,Kpm,Kqm。選用IEEE 39節點系統進行分析，選擇負荷節點3,15,16,18,21,25—29為研究對象，它們各自的負荷用電性質構成比例如表1所示，根據文獻[20]中各類負荷中靜態和動態負荷的典型比例數據，得到這些負荷的綜合模型參數，并將相應的系統仿真結果作為參考系統的實測值。

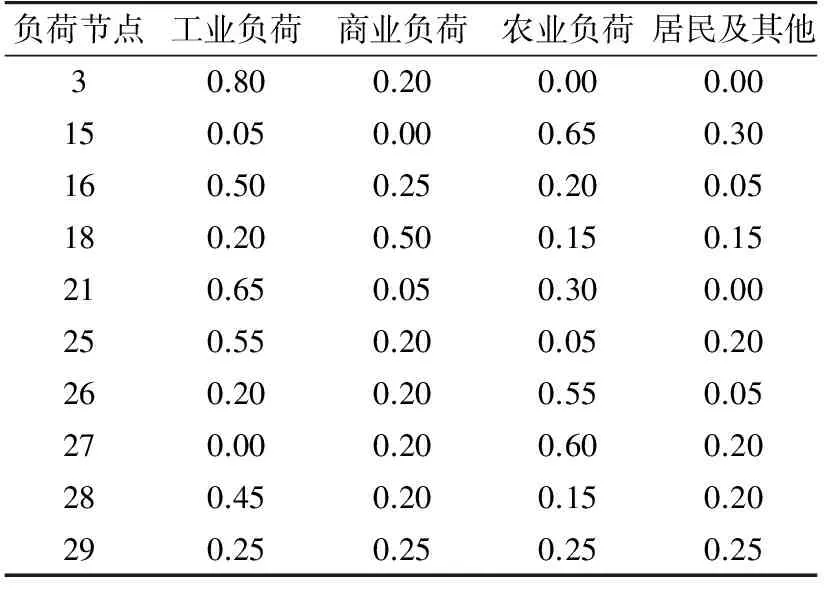
表1 IEEE 39節點系統的負荷用電性質構成比例Tab. 1 Proportion of consumption componentof loads of IEEE 39-bus system

基于文中所提特征對負荷分類并識別得到的負荷模型記為模型系統Ⅰ。為檢驗文中所提分類方法的優劣，選取了另外兩種負荷分類策略，其一為按負荷間電氣距離的大小分類，用該方法分類識別得到的負荷模型記為模型系統Ⅱ；其二為負荷節點不分類，即將待研究負荷節點設定為一類，且各節點具有相同的模型參數，識別得到的模型記為模型系統Ⅲ。設擾動場景為線路16—19距首端20%處發生三相短路，故障持續0.04 s。將系統中所有電壓母線作為候選觀察對象，對其響應曲線進行Prony振蕩模式計算，結果顯示系統發生約2.5 Hz的區間振蕩，振蕩模式如圖2所示，多條母線參與程度均較為接近，其中紅色為母線BUS16，綠色和藍色代表其余母線，因該算例系統無法體現電壓的有名值情況，因此，選取了參與振蕩程度較好且跌落最嚴重的母線BUS16作為系統區域負荷模型識別的觀測母線。

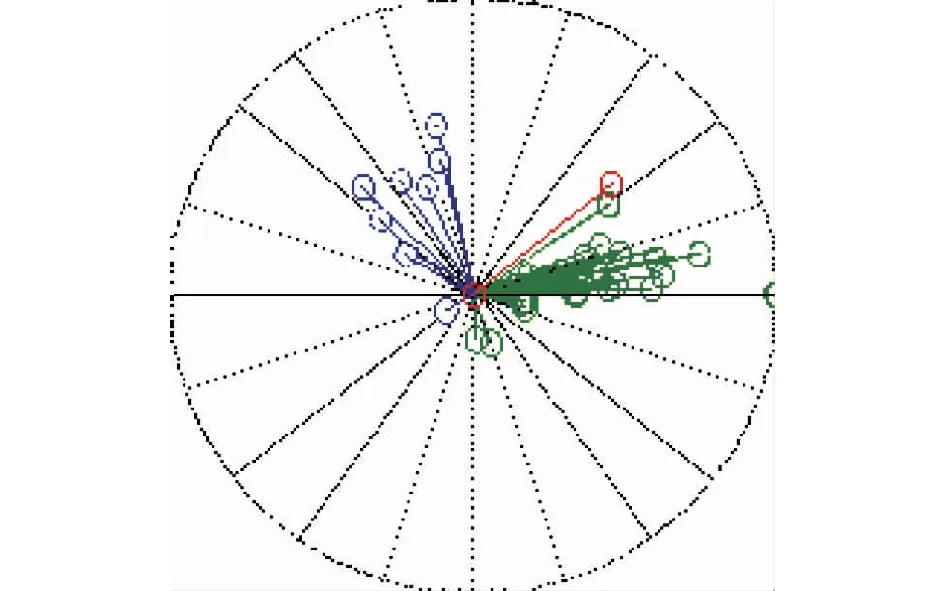
圖2 系統主導區間振蕩模式分析Fig.2 Mode shape of dominant interarea mode

根據各節點負荷用電性質構成比例，基于聚類算法將負荷分為3類：第Ⅰ類為負荷3, 16, 21, 25；第Ⅱ類為負荷15, 26, 27；第Ⅲ類為負荷18, 28, 29。每類負荷待識別參數為Ap,Bp,Aq,Bq,Kpm,Kqm，經靈敏度計算，參數Ap,Kpm,Kqm的靈敏度最高，將它們選取為待識別參數，則系統需識別的負荷參數共9個，為Apfi，Kpmfi，Kqmfi(fi=1,2,3)，其余參數取典型參數值代替，模型系統I的負荷參數識別結果見表2。

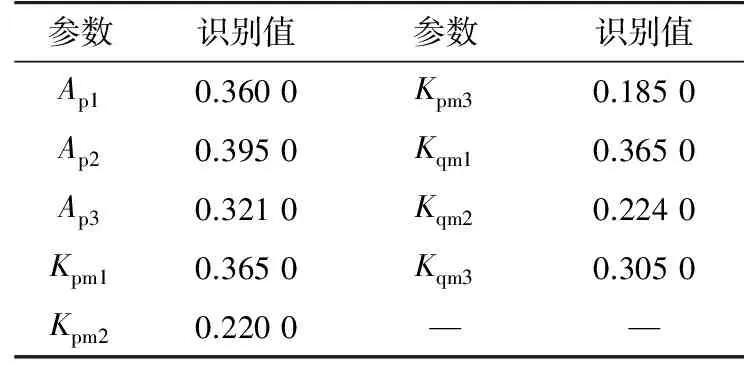
表2 按負荷用電性質比例分類識別的負荷參數Tab. 2 Identification results of load model using theproportion of load consumption componentas the classification characteristics

依據負荷節點間的電氣距離將負荷分類為：3, 15, 21, 26, 27為第Ⅰ類;16, 18, 25為第Ⅱ類;28, 29為第Ⅲ類。在相同的擾動場景下進行參數識別，得到模型系統Ⅱ的負荷參數結果。設所有負荷都有相同的模型參數，在相同的擾動場景下進行參數識別，得到模型系統Ⅲ的負荷參數結果。圖3給出了模型系統Ⅰ—Ⅲ與參考系統的電壓響應。結果表明，不分類識別對應的仿真響應誤差最大，以節點間電氣距離分類識別得到的結果，其誤差次之，以負荷用電性質特征分類識別的模型，其響應與參考系統的電壓軌跡擬合很好。

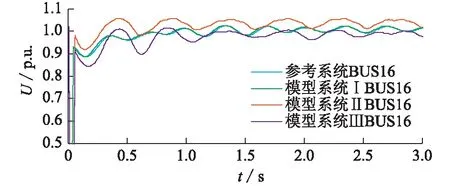
圖3 參考系統和模型系統的觀測對象電壓響應Fig.3 Voltage response of reference and model systems

在某一特定運行場景下識別得到的模型參數能否在其他場景下也較好的反映元件動態，即模型的適用性問題，需要進一步檢驗。各負荷大小及組成保持不變，分別改變系統擾動強度、擾動位置、系統潮流分布和網絡拓撲結構，檢驗在某運行場景中識別得到的模型系統Ⅰ—Ⅲ的參數對其他運行場景的適用性。

(1) 擾動強度影響的檢驗。擾動場景為線路16—15距首端30%處發生三相短路，擾動持續時間τ。τ分別取為0.04 s,0.045 s,0.05 s。BUS15為參考系統觀測母線，當τ=0.04 s時的電壓響應曲線如圖4所示，模型系統Ⅰ與參考系統的電壓響應基本重合，模型系統Ⅱ的電壓響應與參考系統擬合略差，而模型系統Ⅲ的響應曲線與參考系統響應差別最大，其主導振蕩模式頻率明顯增加。表3給出了τ取不同值時的響應誤差J，隨著擾動強度的增加，各模型系統誤差值J都在不斷增大，也顯示出模型系統I的誤差值J總能保持在相對較小的范圍，而模型系統Ⅲ的誤差值最大。

圖4 τ=0.04 s時模型與參考系統電壓響應Fig.4 Voltage response of model and reference system while τ=0.04 s

表3 擾動強度變化時的響應誤差Tab. 3 Response error changedwith the duration of disturbance

(2) 擾動位置影響的檢驗。擾動場景取為線路16—15距首端x%處發生三相短路，持續時間為0.04 s。分別取x為10, 20, 50，BUS15仍為參考系統觀測母線。圖5給出了當x=10時的電壓響應。表4給出了故障發生在不同位置時各模型系統與參考系統的電壓誤差值J。模型系統Ⅰ與參考系統電壓響應的接近程度明顯優于模型系統Ⅱ和Ⅲ，且當擾動地點變化時，模型系統Ⅰ的適用性更好。

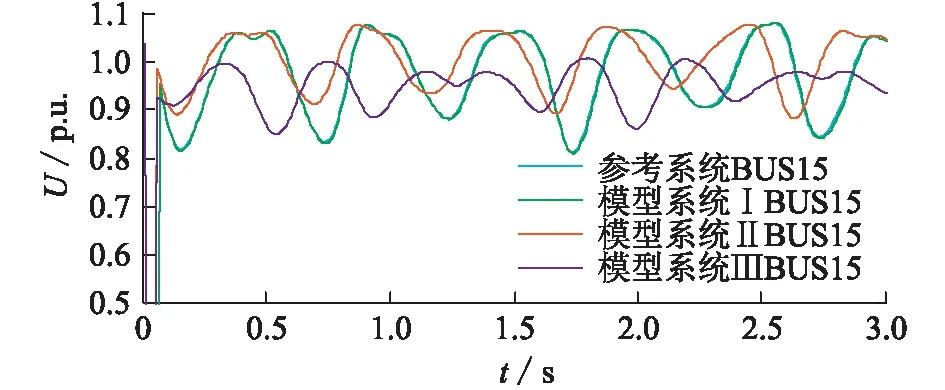
圖5 x=10時模型與參考系統電壓響應Fig.5 Voltage response of model and reference system while x=10

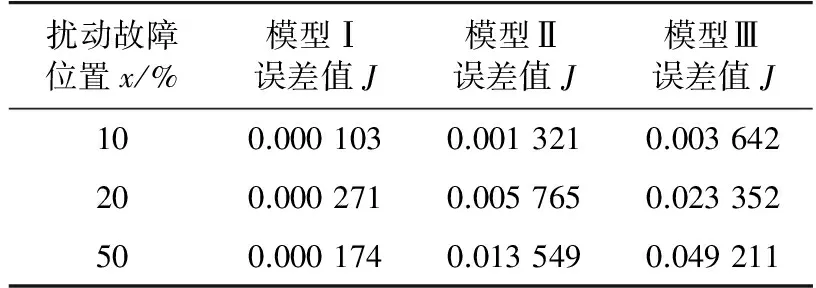
表4 擾動位置變化時的響應誤差Tab. 4 Response error changedwith the disturbance location

(3) 系統潮流分布影響的檢驗。在原始系統的基礎上，僅改變部分機組出力，如表5所示，得到系統的潮流分布Ⅰ—Ⅲ，記初始有功功率為P0，調整后的有功功率為P。擾動場景仍為線路16—15距首端30%處發生三相短路故障，持續時間為0.04 s，BUS15為觀測母線。圖6給出了系統潮流分布為情況Ⅰ時模型系統和參考系統的電壓響應，表6給出了當潮流分布改變后，各模型系統與參考系統的電壓誤差值J。結果顯示，雖然潮流分布變化，但模型系統Ⅰ仍然可以很好的反映參考系統的動態，模型系統Ⅱ和Ⅲ的響應卻與參考系統有較大差距。

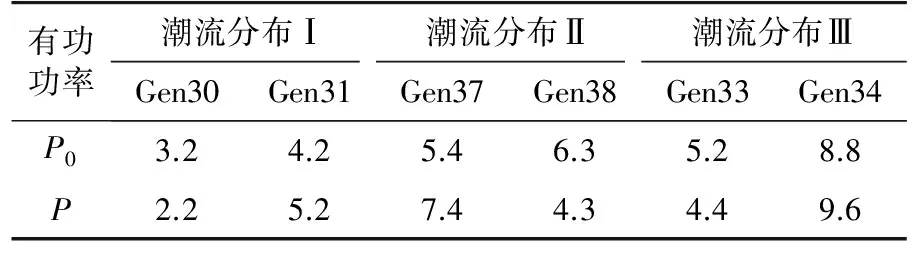
表5 潮流分布情況I—ⅢTab. 5 Power flow distribution I—Ⅲ

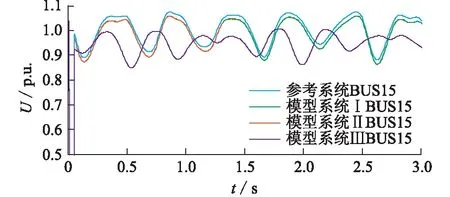
圖6 潮流分布I下模型與參考系統電壓響應Fig.6 Voltage response of model and reference system with flow distribution I

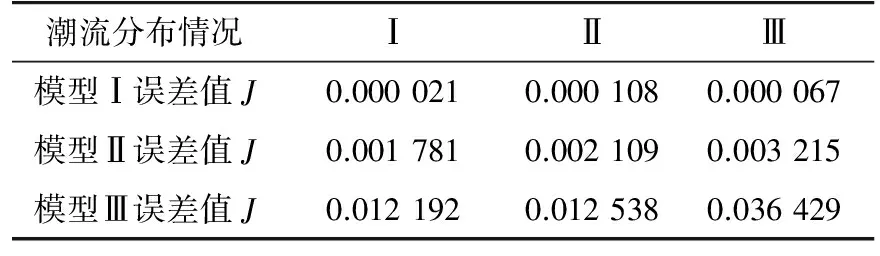
表6 潮流分布變化時的響應誤差Tab. 6 Response error with flow distribution changed

(4) 網絡拓撲結構影響的檢驗。在原始系統基礎上僅切除線路5—6得到拓撲結構Ⅰ，僅切除線路13—14得到拓撲結構Ⅱ，僅切除線路6—11得到拓撲結構Ⅲ。擾動場景為線路16—15距首端10%處發生三相短路，擾動持續時間為0.03 s。BUS15為觀測母線。圖7給出了拓撲結構Ⅰ時系統的電壓響應，表7給出了當拓撲改變后，各模型系統與參考系統的電壓誤差J。結果表明模型系統Ⅰ適應其他拓撲結構的能力更強。

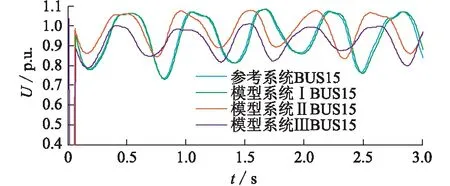
圖7 拓撲結構I下模型與參考系統電壓響應Fig.7 Voltage response of model and reference system with grid topology I

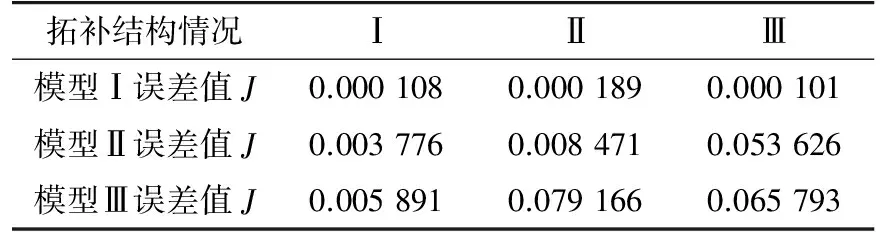
表7 網絡拓撲結構變化時的響應誤差Tab. 7 Response error changed with the grid topology

綜上，當保持各節點負荷的大小和組成不變，僅改變系統其他運行條件，按負荷用電性質構成比例分類得到的參數識別結果具有良好的精度和適用能力，遠優于按負荷節點所屬區域分類和不分類兩種情況下的識別結果，而不分類的負荷模型識別結果，其精度和適用性最差。

3.2 IEEE 118節點系統仿真

本節選取IEEE 118節點系統再次對上述分類識別方法進行檢驗。選取27個負荷節點作為研究對象，各節點負荷用電性質構成比例如表8所示。擾動場景為線路6—7距首端母線30%處發生三相短路，持續時間為0.05 s，將系統中220 kV以上電壓母線作為候選觀察對象，對其響應曲線進行Prony振蕩模式計算，結果顯示系統發生約0.4 Hz的區間振蕩，振蕩模式如圖8所示，其中紅色為500 kV 母線BUS20，位于區域間的聯絡線上，綠色和藍色代表其余母線，鑒于BUS20充分參與了系統的區間振蕩，且電壓等級高，因此將其選為系統區域負荷模型識別的觀測母線。以負荷用電性質構成比例分類，結果如表9所示，經過靈敏度計算，參數Ap,Bp,Kpm的靈敏度較大，表10給出了模型參數的識別結果。

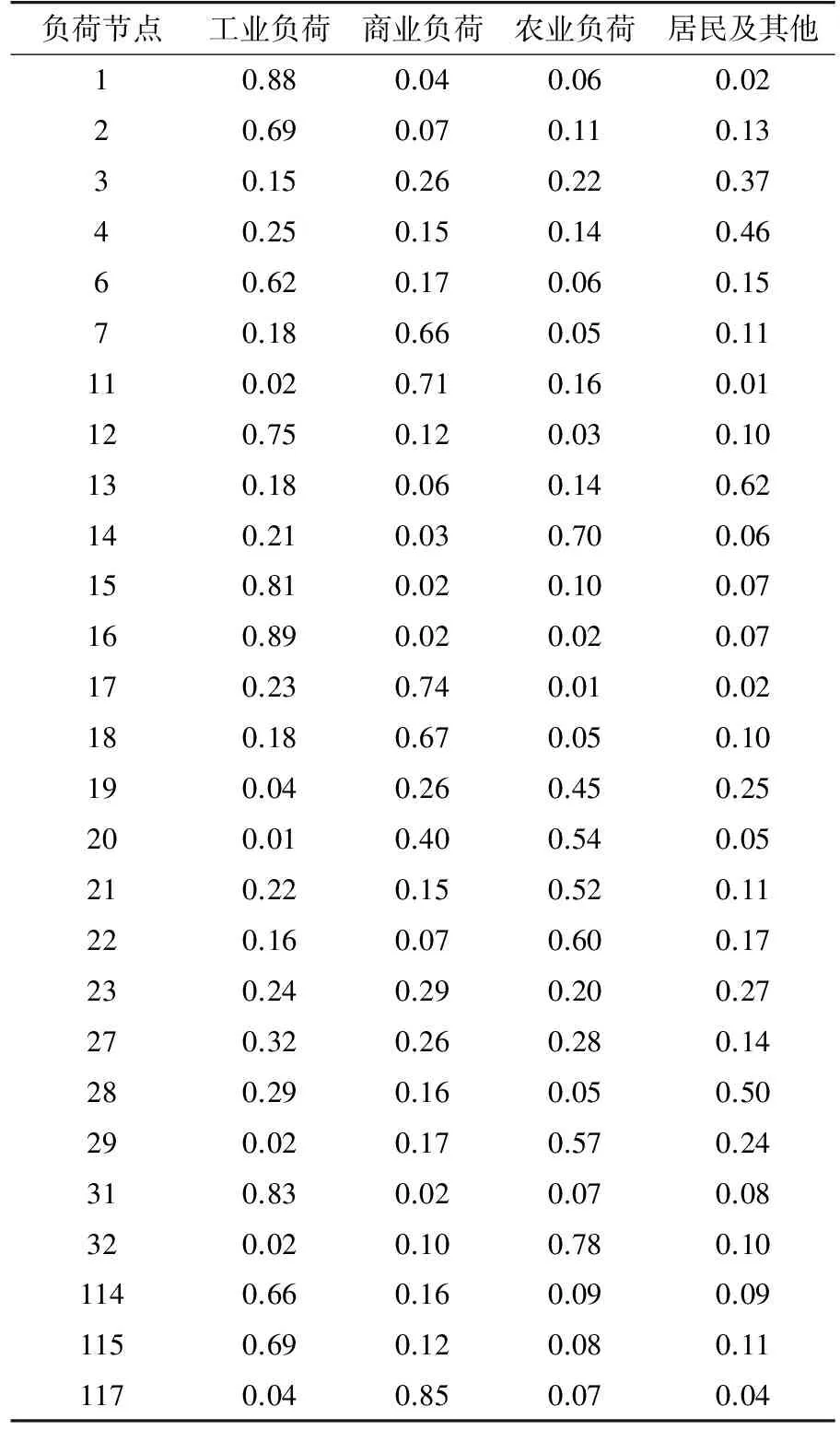
表8 IEEE 118節點系統的負荷用電性質構成比例Tab. 8 Proportion of load consumption component ofloads in IEEE 118-bus system

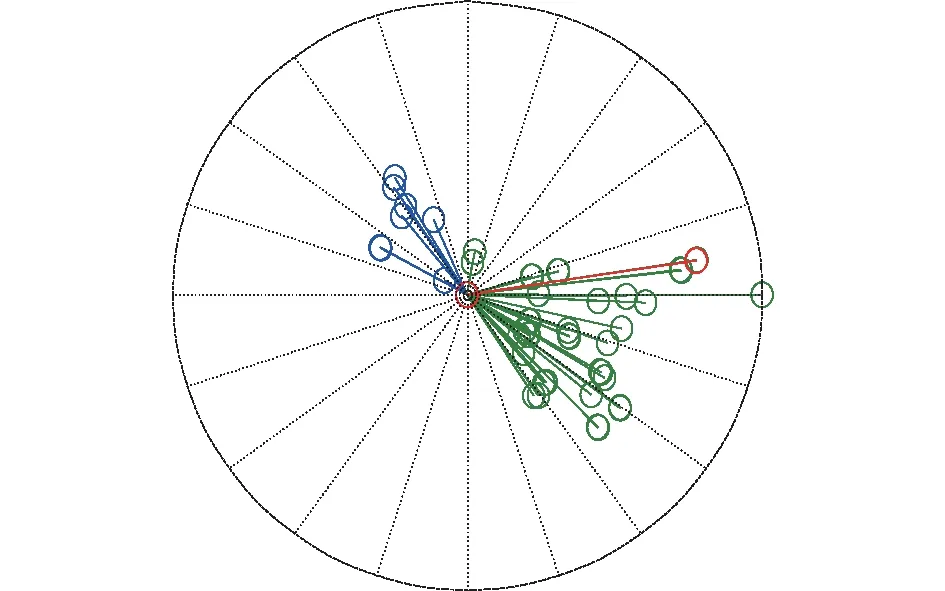
圖8 系統主導區間振蕩模式分析Fig.8 Mode shape of dominant interarea mode

表9 根據負荷用電性質構成比例進行分類Tab. 9 Load classification based on proportionof load consumption component

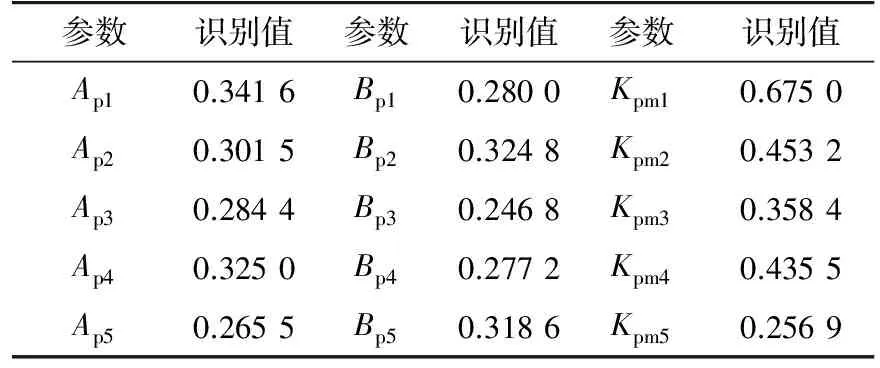
表10 按負荷用電性質比例分類識別的負荷參數Tab. 10 Identification results of load model usingthe proportion of load consumption component as theclassification characteristics

同4.1節，選用不同分類特征對負荷分類識別得到的模型系統響應曲線如圖9所示。通過計算，模型系統Ⅰ、Ⅱ和Ⅲ與參考系統的響應誤差值J分別為0.000 401,0.000 913,0.001 124，該算例進一步說明文中所提負荷分類識別方法的有效性。

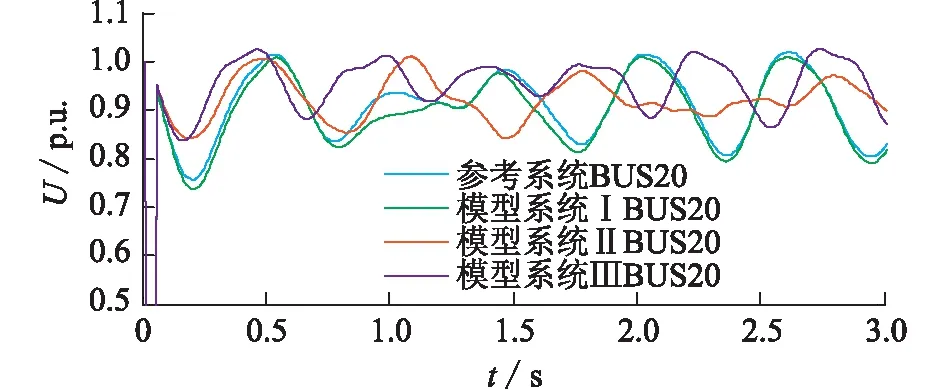
圖9 參考系統和模型系統的電壓響應Fig.9 Voltage response of reference and model system

5 結語

選取不同用電性質負荷占所接入負荷節點總負荷量的比例作為負荷節點的分類特征，采用模糊C均值聚類算法對負荷節點進行分類，認為同一類負荷節點具有相同的負荷參數，進行負荷模型識別。為了在不增大觀察維度的前提下充分反映區域負荷對電網動態的整體影響，利用Prony算法從實測信號中提取系統振蕩模式，并識別其中的主導振蕩模式，用參與主導振蕩模式的高電壓級別母線作為觀測母線，并用觀測母線的電壓建立參數識別的目標函數及主導參數的選擇方法，用優化算法對主導參數尋優，獲得負荷模型。在IEEE 39節點和IEEE 118節點系統上進行檢驗，通過多種分類策略下的負荷參數識別結果優劣的比較，表明按負荷用電性質構成比例分類識別的方法，得到的負荷模型識別結果具有更好的適用性。

[1] 郝麗麗, 岳浩永, 張恒旭, 等. 分類策略對廣域系統負荷識別結果適應性的影響分析[J]. 電網技術, 2014, 38(2):381-387.

HAO Lili, YUE Haoyong, ZHANG Hengxu, et al. Influence analysis of classification strategy on wide area system load identification result adaptablity [J]. Power System Technology, 2014, 38(2): 381-387.

[2] WALVE K. Modeling of power system components at severe disturbances[C]∥CIGRE Meeting, Paris, France, 1986.

[3] KOSTEREV D N, TAYLOR C W, MITTELSTADT W A. Model validation for August 10, 1996 WSCC system outage[J]. IEEE Transactions on Power Systems, 1999, 14(3): 967-979.

[4] VENKATASUBRAMANIAN V, LI Y. Analysis of 1996 Western American electric blackouts[C]∥Bulk Power System Dynamics and Control-VI, Cortinad Ampezzo, Italy, 2004.

[5] 方勇杰. 美國9.8大停電對連鎖故障防控技術的啟示[J]. 電力系統自動化, 2012, 36(15): 1-7.

FANG Yongjie. Lessons from September 8, 2011 southwest America blackout for prevention and control of cascading outages [J]. Automation of Electric Power Systems, 2012, 36(15): 1-7.

[6] CHICCO G. Overview and performance assessment of the clustering methods for electrical load pattern grouping[J]. Energy, 2012, 42(1):68-80.

[7] 鞠 平, 金 艷, 吳 峰, 等. 綜合負荷特性的分類綜合方法及其應用[J]. 電力系統自動化, 2004, 28(1):64-68.

JU Ping, JING Yan, WU Feng, et al. Studies on classification and synthesis of composite dynamic loads [J]. Automation of electric power systems, 2004, 28(1):64-68.

[8] MAHMOUDI-KOHAN N. An annual framework for clustering-based pricing for an electricity retailer[J]. Electric Power Systems Research, 2010, 80(9):1042-1048.

[9] 鄭曉雨, 賀仁睦, 馬 進, 等. 基于軌跡靈敏度的負荷分類[J]. 電工技術學報, 2010, 25(9):145-150.

ZHENG Xiaoyu, HE Renmu, MA Jin, et al. A method of load classification based on the trajectory sensitivity [J]. Transactions of china electro technical society, 2010, 25(9):145-150.

[10] 李欣然, 林舜江, 劉楊華, 等. 基于實測響應空間的負荷動特性分類原理與方法[J]. 中國電機工程學報, 2006, 26(8):39-44.

LI Xinran, LIN Shunjiang, LIU Yanghua, et al. A new classification method for aggregate load dynamic characteristics based on field measured response [J]. Proceedings of the CSEE. 2006, 26(8):39-44.

[11] 石景海, 賀仁睦. 動態負荷建模中的負荷時變性研究[J]. 中國電機工程學報. 2004, 24(4):85-90.

SHI Jinghai, HE Renmu. Load time-variantion study in dynamic load modeling[J]. Proceedings of the CSEE. 2004, 24(4):85-90.

[12] 張紅斌, 賀仁睦, 劉應梅. 感應電動機負荷模型參數靈敏度分析及參數辨識策略研究[J]. 電網技術, 2004, 28(6):10-14.

ZHANG Hongbing, HE Renmu, LIU Yingmei. Analysis on parameter analytic sensitivity of induction motor load model and parameter identification strategy [J]. Power System Technology, 2004, 28(6): 10-14.

[13] 鞠 平, 陳 謙, 熊傳平, 等. 基于日負荷曲線的負荷分類和綜合建模[J]. 電力系統自動化, 2006, 30(16): 6-9.

JU Ping, CHEN Qian, XIONG Chuanping, et al. Load clustering and synthetic modeling based on daily load curves [J]. Automation of electric power systems, 2006, 30(16):6-9.

[14] WANG Z S, BIAN S R,et al. The load characteristics classification and synthesis of substations in large area power grid[J]. International Journal of Electrical Power and Energy Systems, 2013, 48(1):71-82.

[15] 汪小明, 劉滌塵, 吳 軍, 等. 電力系統暫態穩定分析廣義負荷模型[J]. 電網技術, 2011, 35(3):44-48.

WANG Xiaoming, LIU Dichen, WU Jun, et al. A generalized load model for transient stability analysis of power system [J]. Power System Technology, 2011, 35(3):44-48.

[16] 朱建全, 李 穎, 譚 偉. 基于特性融合的電力負荷建模[J]. 電網技術, 2015, 39(5):1358-1364.

ZHU Jianquan, LI Ying, TAN Wei. Characteristic fusion based on electric load modeling [J]. Power System Technology, 2015, 39(5):1358-1364.

[17] 申定輝，于曉蕾，吳 丹. 基于混合高斯模型的配電網負荷偽量測權重優化算法[J]. 廣東電力，2016，29(5)：86-91，123.

SHEN Dinghui, YU Xiaolei, WU Dan. Optimization algorithm for pseudo measurement weight of power distribution network load based on Gaussian mixture model[J]. Guangdong Electric Power，2016，29(5)：86-91，123.

[18] HAN D, MA J, HE R M, et al. A real application of measurement-based load modeling in large-scale power grids and its validation[J]. IEEE Transactions on Power Systems, 2009, 24(4): 1756-1764.

[19] 黃 梅, 賀仁睦, 楊少兵, 等. 東北電網負荷模型的分類與應用[J]. 電力系統自動化, 2005, 29(4):85-87.

HUANG Mei, HE Renmu, YANG Shaobing, et al. Application of load model classification in northeast power network [J]. Automation of Electric Power Systems, 2005, 29(4):85-87.

[20] 張樹卿, 韓英鐸, 于松泰, 等. 區域綜合負荷動態等值參數在線測辨關鍵技術[J]. 電力系統自動化, 2012, 36(19):114-121.

ZHENG Shuqing, HAN Yingduo, YU Songtai. et al. Key techniques for composite load area integral equivalence and online parameter identification [J]. Automation of Electric Power Systems, 2012, 36(19):114-121.

[21] 鞠 平. 電力系統負荷建模理論與方法[M]. 北京: 科學出版社, 2010.

JU Ping. Power system load modeling theory and method[M]. Beijing:Science Press,2010.