基于高維隨機矩陣的系統狀態評估方法研究

程含渺, 李紅斌, 徐 晴, 紀 峰, 陳 剛 , 田正其

(1. 國家電網公司電能計量重點實驗室(國網江蘇省電力有限公司電力科學研究院), 江蘇 南京 210019；2. 華中科技大學電氣與電子工程學院，湖北 武漢 430074)

0 引言

元素為隨機變量的矩陣稱為隨機矩陣，最初源于數理統計研究，經過數十年發展，隨機矩陣理論逐步完善。20世紀50年代，物理學家Wigner證明了半圓律[1-2]。1976年，馬爾琴科和帕斯圖證明了馬爾琴科-帕斯圖(M-P)定理[3]。目前，隨機矩陣理論已應用于核物理、多元統計、無線電通信、經濟學、生物學等領域[4-10]。近兩年，電力數據分析引入了大數據方法[11-15]，高維隨機矩陣作為一種處理工具，也開始嶄露頭角。

文獻[16]首次用高維隨機矩陣對電網運行數據進行建模分析。文獻[17—18]在此基礎上，著重研究了高維隨機矩陣在負荷關聯分析的應用。文獻[19]研究了高維隨機矩陣在廣域量測數據異常檢驗方面的應用。文獻[20]研究了使用高維隨機矩陣方法評估變壓器運行健康狀態，并將其與傳統方法進行了比較。

雖然高維隨機矩陣理論在狀態評估方面的研究文獻較多，但在基礎性方面還不完善：(1) 沒有描述高維隨機矩陣的適用性；(2) 評估判據指標只有平均譜半徑(mean spectral radius，MSR)；(3) 數據處理步驟復雜。文中在現有研究成果的基礎上，提煉了高維隨機矩陣的應用條件，闡述了應用方法，提出了另2個狀態評估指標量，討論了單環定理的編程步驟，以電力設備健康狀態評估和電網運行狀態評估為例進行了應用仿真。

1 高維隨機矩陣數學基礎

高維隨機矩陣理論屬于多元統計學研究領域，極限譜分布是其重要研究內容，以下介紹與狀態評估密切相關的2個重要譜分布[21-24]。

1.1 馬爾琴科-帕斯圖定理

令隨機矩陣X=(xij)n×m，矩陣X任意列中的元素xkj(k=i,j=1,2,…)是均值為0，方差為σ2的獨立同分布隨機變量，則矩陣X的樣本協方差矩陣定義為：

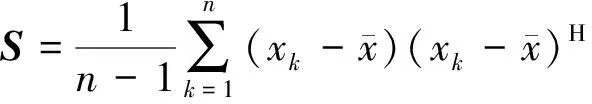
(1)

式中：xk為矩陣Xn的第k列。在一般情況下，矩陣Xn的樣本協方差也可以簡單定義為：

(2)

式中：Sn為Wishart矩陣。當m/n→c∈(0,∞)，Sn的極限譜分布依概率收斂到概率密度函數為式(3)的譜分布函數，簡稱為M-P律，且當σ2=1時，稱為標準M-P律。

(3)

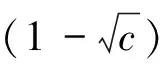
1.2 單環定理

假設隨機矩陣A=(xij)n×n可以分解為A=PTQ，其中P和Q為n階Haar酉矩陣，T是對角陣，對角線元素是A的奇異值。當滿足一定的條件時，矩陣A的極限譜分布由其奇異值的概率測度唯一確定，且特征值在復平面上收斂到圓環，圓環的內外半徑分別為：

(4)

式中：v為矩陣A的奇異值的概率測度。在實際應用中，考慮矩陣A=(xij)∈Cp×N為非-Hermitian矩陣，其元素為獨立同分布的隨機變量，且矩陣A的列向量滿足均值為0、方差為1。對于L個矩陣Ai，定義矩陣乘積Z為：

(5)

式中：Au,i為Ai的奇異值等價矩陣。將矩陣Z標準化為Zstd，使其滿足σ2(zi)=1/N，則Zstd的極限譜分布依概率收斂到概率密度函數為式(6)的譜分布函數。

(6)

式中：λz為特征值；d為p/N∈{(0,1]，p,N→∞}。Zstd的特征值在復平面的分布是一個圓環，內環半徑為(1-d)L/2，外環半徑為1。

2 高維隨機矩陣應用方法

2.1 適用條件

一般來說，表征系統狀態的可測狀態參量有N個，假設分別為{P1,P2,…,PN}，可測是指可以直接或間接測量。現對可測狀態參量Pi(i=1,2,…,N)與系統狀態的關系作如下3個一般性假設。

(1) 理想狀態下，N個可測狀態參量保持基本恒定不變，僅在均值水平附近正態隨機波動，且這種隨機波動過程是平穩的，則第i個狀態參量在任意時刻的測量值pim為：

pim=μ(pi)+εi

(7)

式中：μ(pi)為第i個可測狀態參量的均值水平；εi為第i個可測狀態參量的隨機波動量；波動量應滿足μ(εi)=0，σ2(εi)=const(const為常量)。

(2) 若第i個可測狀態參量的測量值出現異常波動，不再是平穩正態隨機波動，即μ(εi)≠0或σ2(εi)≠const，則懷疑該系統的狀態存在變化。

(3) 若有多個可測狀態參量出現(2)所描述的情況，則有更加充分的理由懷疑系統狀態發生了變化。

需要說明的是，當應用條件不滿足上述基本假設條件時，可以對可測量進行適當變換。例如，在文獻[19]中，對變壓器各狀態參量的測量數據用AR(1)、ARMA(1,1)等低階模型擬合，再求殘差序列，用殘差值構建高維隨機矩陣。

2.2 高維矩陣構建方法

假設在狀態評估時間窗內，對系統的K個可測狀態參量測量T次，則在截取的時間窗內，所有測量數據可以構成K行T列矩陣：

(8)

式中：矩陣D的元素xij表示第i個可測狀態參量在j時刻的測量值。當K和T充分大，并且K和T是同一數量級時，矩陣D是一個高維隨機矩陣。對矩陣D進行標準化，使標準化之后的矩陣Dstd=(yij)K×T滿足：

(9)

式中：yi=(yi1,yi2,…,yiT),1≤i≤K，則矩陣Dstd一般為非-Hermitian矩陣。當K,T→∞且K/T→c時，矩陣Dstd滿足如下性質：(1) 樣本協方差矩陣的極限譜分布滿足標準M-P律；(2) 奇異值等價矩陣通過Haar酉矩陣變換得到的標準化乘積矩陣應滿足標準單環定理。

可以通過檢驗Dstd是否滿足上述性質來評估設備或系統的可測狀態參量是否發生異常波動。為了檢驗Dstd是否偏離上述性質，需要選擇合適的統計量作為評估判據指標。

2.3 評估判據指標

2.3.1 譜分布概率密度函數相似度判據

假設正常狀態時，由狀態量測量值構成的隨機矩陣的樣本協方差矩陣為S1，S1的特征值分布概率密度函數為f1(x)。當狀態發生變化時，其狀態量測量值構成的隨機矩陣的樣本協方差矩陣為S2，S2的特征值分布概率密度函數為f2(x)。顯然，狀態變化前后的S1和S2有差異，對應的f1(x)和f2(x)也會有差異。因此，可以將f1(x)和f2(x)的差異程度作為狀態變化的定量評估判據指標。

設有2個概率密度函數f1(x),x∈[b1,h1]和f2(x),x∈[b2,h2]，定義概率密度函數的差異程度υ為：

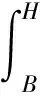
(10)

式中：B=min(b1,b2)，H=min(h1,h2)。υ越小表示2個概率密度函數的差異越小。在實際應用中，可以將f1(x)和f2(x)分別與標準M-P律求差異度，再比較兩個差異度的大小。

2.3.2 特征值線性統計量判據

正常狀態下，服從單環定理的特征值會均勻分布在圓環內，若狀態發生異常變化，特征值分布會隨之變化，分布不再均勻，導致圓環的形態改變。因此，可以使用特征值的分布環半徑以及分布集中程度作為狀態是否變化的評估判據指標，通常用矩統計量表征。

假設隨機變量的一個樣本為X={X1,X2,…,Xn}，則該樣本的k階中心矩αk為：

(11)

式中：E(X)為樣本期望。同理，可以定義樣本的k階原點矩βk為：

(12)

對于隨機矩陣的n階樣本協方差矩陣Sn×n，若Sn×n的特征值為λ={λ1,λ2,…，λn}，其一階原點矩的物理意義是平均譜半徑，二階中心矩的物理意義是特征值距離平均譜半徑的距離平方和。因為特征值分布越集中，平均譜半徑越大，所以可以采用一階原點矩β1和二階中心矩α2作為狀態評估判據指標。

3 單環定理編程步驟

單環定理編程步驟實際上也是高維測量數據的處理方法，文獻[16—20]已經進行了具體闡述，但過程復雜。文中在上述文獻的研究基礎上，對編程步驟作了進一步討論。

依照單環定理的描述，在獲得原始數據矩陣X之后，應求取矩陣T，具有以下性質[23-24]：(1) 是一個對角矩陣；(2) 對角線元素是矩陣A的奇異值；(3) 矩陣A是將T用2個Haar酉矩陣進行變換得到。根據單環定理的描述，在使用數學工具如Matlab編程時，具體步驟如下:

(1) 將n個變量的測量數據xi(ti)按照時間順序排列，再分段截取構成待處理的原始高維矩陣X；

(2) 用奇異值分解函數對原始矩陣X作奇異值分解，得到對角矩陣Xsng，該過程不依賴Haar酉矩陣；

(3) 生成2個標準Haar酉矩陣U和V，按照式(13)將Xsng變換為矩陣Zorg：

Zorg=UXsngV

(13)

(4) 將矩陣Zorg按照式(9)標準化得到Zstd，最后再求Zstd的特征值。

依照上述4個步驟，Zstd的特征值分布呈標準的單環。關于Haar酉矩陣的生成方法，可以參看文獻[25]，矩陣Zorg的標準化方法可以參看文獻[16—20]，在運算過程中，還要注意矩陣的行列數符合矩陣運算條件。

4 電力設備健康狀態評估

電力設備健康狀態往往由多個參量共同決定，變壓器的狀態參量包括油中溶解氣體、絕緣電阻、介質損耗、油中微水等，斷路器狀態參量包括觸頭電磨損、分合閘線圈電流、開斷行程等。將這些狀態量的測量值，構建成高維隨機矩陣，則可以通過分析矩陣性質評估電力設備健康狀態。

假設某電力設備的可測狀態參量有3個，記為P1,P2,P3。在正常狀態下，這3個可測狀態量在其均值附近隨機波動。在某一時刻，由于狀態發生惡化，導致狀態量P3出現異常(或者可測狀態量P3出現異常，導致狀態惡化)。3個狀態參量的測量數據曲線如圖1所示。

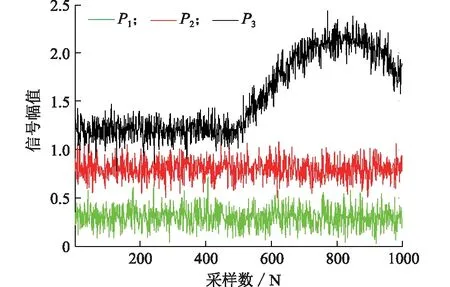
圖1 設備可測狀態參量的數據曲線Fig.1 Measured parameter data curve of equipment

圖中：信號幅值單位為1，采樣數據一共為1000組，假設在第500組采樣點處狀態量P3發生異常波動，持續時間為500組采樣點。

4.1 第一組數據仿真

數據取自圖1中的1—500組采樣點，得到一個3×500矩陣，采用文獻[21]的矩陣擴充方法將矩陣擴充為300×500矩陣。根據M-P律和單環定理實施方法，得到的仿真結果如圖2所示。

圖2 第一組仿真結果Fig.2 The first simulation results

4.2 第二組數據仿真

數據取自圖1中的501—1000組采樣點，參照第一組仿真過程，得到的仿真結果如圖3所示。

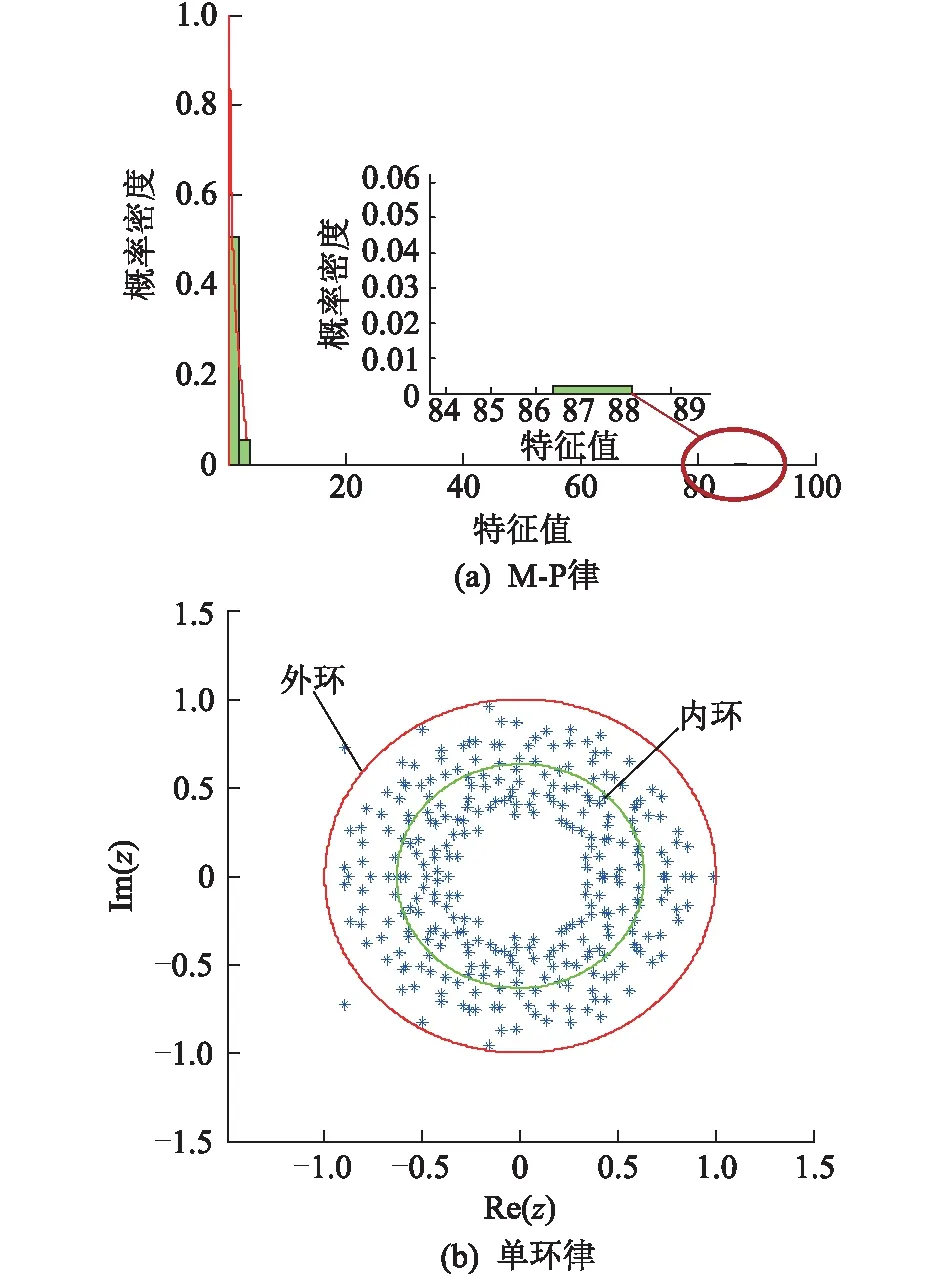
圖3 第二組仿真結果Fig.3 The second simulation results

從2組仿真結果可以看出，第一組與第二組的仿真結果有明顯差異，具體表現在：(1) 第二組仿真結果出現了重大特征值，偏離M-P律的程度變大；(2) 第二組仿真結果中特征值超出圓環內徑，環內的特征值分布更分散。若將2.3.1中的3個定量評估判據指標記為J1,J2,J3，分別計算兩組仿真結果的判據量化值，結果如表1所示。

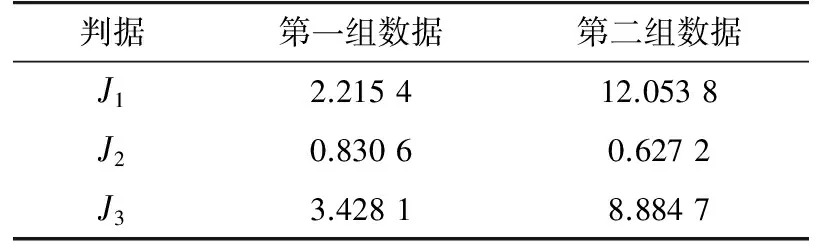
表1 評估判據指標計算結果Tab.1 The calculation results of evaluation criterion

從表1可以看出，當設備或系統的可測狀態量數據出現異常時，判據量化值具有顯著變化。第二組數據的仿真結果與第一組相比：(1)J1變大，說明第二組數據偏離M-P律的程度變大；(2)J2變小，說明第二組數據的單環平均半徑變小，特征值向中心分散；(3)J3變大，環內的特征值分布更分散。在實際應用時，適當選擇滑動時間窗，實時計算3個評估判據指標，得到3條指標曲線，則可以根據曲線的波動情況對設備狀態進行評估。

5 電網運行狀態評估

評估電網運行狀態一般需要依賴電網拓撲結構，但隨著電網規模越來越大，拓撲結構變得越來越復雜，建模分析難度也隨之增大。可以對電網節點電壓數據構建高維矩陣，通過分析矩陣性質從而評估電網運行狀態，從而實現依賴于電網拓撲結構的狀態評估，文獻[26]也進行了類似探索研究。采用Power System Toolbox(PST)仿真工具，針對圖4所示的新英格蘭10機39節點典型電力系統，對基于高維隨機矩陣理論的電網運行異常狀態評估方法進行了仿真驗證。仿真時間步進設置為0.01 s，仿真時長設置為2 s，假設在第1.8 s時，線路3-4發生對地三相短路故障，隨后故障恢復，1.85 s時清除近端故障告警，1.9 s時清除遠端故障告警，相關斷路器先后合閘，母線節點電壓仿真結果如圖5所示。

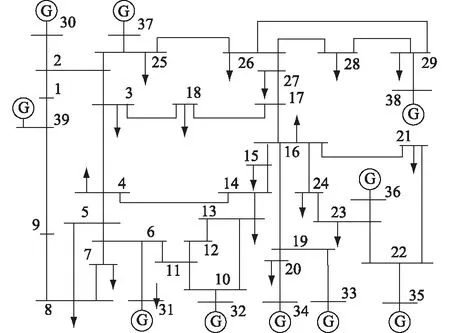
圖4 新英格蘭10機39節點系統Fig.4 The New-England 10-generator 39-bus system

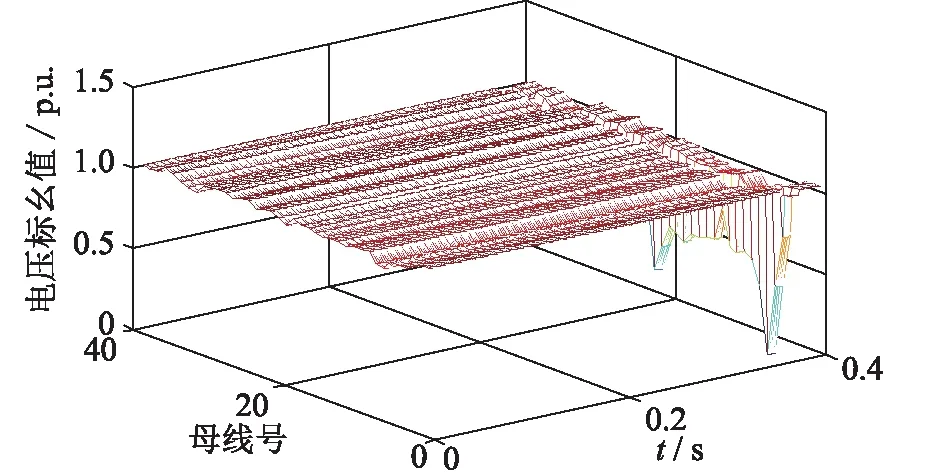
圖5 節點電壓仿真結果Fig.5 Simulation result of bus voltage

由圖5可知，在1.85 s故障發生時，各母線電壓出現了不同程度跌落，3號母線電壓跌落至零，距離3號母線越遠，電壓跌落程度越小。用高維隨機矩陣的方法識別本次故障，第一組數據取第1 s內的運行結果，第二組數據取第2 s內的運行結果。參照式(8)，構建39行100列的矩陣，計算結果如圖6所示，定量評估判據指標計算結果如表2所示。

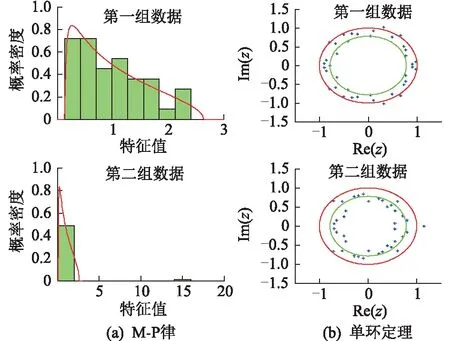
圖6 高維隨機矩陣處理所得結果Fig.6 Results obtained after handling with large dimensional random matrices

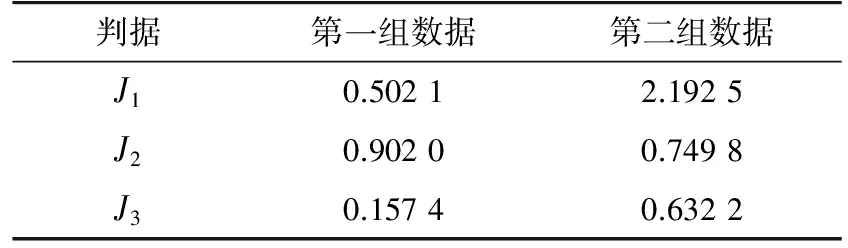
表2 評估判據指標計算結果Tab.2 The calculation results of evaluation criterion

從仿真結果可以看出，與應用于電力設備狀態評估的結果類似，當電網發生故障時，矩陣譜分布偏離M-P律和單環律，與電網正常狀態時的計算結果相比，有明顯差異。對于圖6中的第二組數據計算結果而言，圖6(a)在15處出現異常特征值，圖6(b)的特征值分布超出圓環范圍。

6 結語

文中提煉了高維隨機矩陣應用條件，即在系統正常穩定時，其表征系統狀態的可測參量本身或經處理后是平穩隨機變量。總結了高維隨機矩陣應用方法，著重討論了單環定理實現步驟，其關鍵是第2步和第3步。列舉了兩個應用實例，仿真結果表明，應用高維隨機矩陣的方法，可以識別設備或系統狀態變化。本文對將高維隨機矩陣應用于評估系統狀態的研究者具有參考價值。

[1] WIGNER E P. Characteristic vectors of bordered matrices with infinite dimensions [J]. Annals of Mathematics, 1955, 62(3): 548-564.

[2] WIGNER E P. On the distribution of the roots of certain symmetric matrices [J]. Annals of Mathematics, 1958, 67(2): 325-327.

[3] MARCHENKO V, PASTUR L. Distributions of eigenvalues for some sets of random matrices [J]. Mathematics of the USSR-Sbornik, 1967(1): 457-483.

[4] FEINBERG J, ZEE A. Non-hermitian random matrix theory: method of hermitian reduction[J]. Nuclear Physics B, 1997，504(3): 579-608.

[5] 姜丹丹, 白志東. 大維隨機矩陣譜理論在多元統計分析中的應用[M]. 北京：知識產權出版社，2014.

JIANG Dandan，BAI Zhidong. Application of large dimensional random matrix spectral theory in multivariate statistical analysis[M]. Beijing: Intellectual Property Press,2014.

[6] JOSEPH A, GUO T, QIU R C. Visualization of large wireless network behavior using random matrix theory [C]∥In Proceedings of 2015 IEEE Wireless Communications and Networking Conference. 2015: 2097-2102.

[7] 白志東, 方兆本, 梁應敞. 高維隨機矩陣的譜理論及其在無線通信和金融統計中的應用[M]. 合肥: 中國科學技術大學出版社, 2009.

BAI Zhidong，FANG Zhaoben，LIANG Yingchang. Spectral theory of high dimensional random matrices and its applications in wireless communication and financial statistics[M]. Hefei：China University of Science and Technology Press，2009.

[8] 韓 華, 吳翎燕, 宋寧寧. 基于隨機矩陣的金融網絡模型[J]. 物理學報，2014，63(13)：431-440.

HAN Hua, WU Lingyan, SONG Ningning. Financial networks model based on random matrix [J]. Acta Physica Sinica, 2014, 63(13)：431-440.

[9] PLEROU V, GOPIKRISHNAN P, ROSENOW B, et al. A random matrix approach to cross-correlations in financial data [J]. Physical Review E, 2002, 65: 1-19.

[10] 李 蓉, 顏平蘭, 陳 健, 等． 隨機矩陣理論在肺癌基因網絡識別中的應用[J]． 物理學報，2009，58(10)：6703-6708.

LI Rong, YAN Pinglan, CHEN Jian, et al. Application of random matrix theory to identification of lung cancer gene networks [J]. Acta Physica Sinica, 2009，58(10)：6703-6708 .

[11] 許海清, 黃 敏. 淺談電力大數據對信息運行的影響[J]. 江蘇電機工程, 2015，34(2)：62-64.

XU Haiqing, HUANG Min. A discussion on the influence of power big data on information operation [J]. Jiangsu Electrical Engineering, 2015，34(2)：62-64.

[12] 張友強，寇凌峰，盛萬興，等. 配電變壓器運行狀態評估的大數據分析方法[J]. 電網技術, 2016, 40(3)：768-773.

ZHANG Youqiang, KOU Lingfeng, SHENG Wanxing, et al. Big data analytical method for operating state assessment of distribution transformer [J]. Power System Technology, 2016, 40(3)：768-773.

[13] 李 剛，劉 燕，宋 雨，等. 基于信息融合的電力大數據可視化預處理方法[J]. 廣東電力，2016，29(12)：10-14.

LI Gang, LIU Yan, SONG Yu, et al. Visualization pretreatment method for electric power big data based on information fusion[J]. Guangdong Electric Power，2016，29(12)：10-14.

[14] 張 魁，王亞明，劉 明，等. 基于大數據及智能算法的連云港電量負荷預測研究[J]. 江蘇電機工程, 2016，35(3)：49-52.

ZHANG Kui, WANG Yaming, LIU Ming, et al. Research on electricity consumption and load prediction of Lianyungang based on big data and intelligent algorithm [J]. Jiangsu Electrical Engineering, 2016，35(3)：49-52.

[15] 鄭海雁，金 農，季 聰，等． 電力用戶用電數據分析技術及典型場景應用[J]． 電網技術，2015，39(11)：3147-3152.

ZHENG Haiyan，JIN Nong，JI Cong，et al． Analysis technology and typical scenario application of electricity big data of power consumers [J]． Power System Technology，2015，39(11)：3147-3152.

[16] HE X, AI Q, QIU R C , et al. A big data architecture design for smart grids based on random matrix theory [J]. IEEE Transactions on Smart Grid, 2017，8(2)：674-686.

[17] XU X , HE X，AI Q, et al. A correlation analysis method for power systems based on random matrix theory [J]. IEEE Transactions on Smart Grid, 2015(99):1-10.

[18] 徐心怡, 賀 興, 艾 芊, 等. 基于隨機矩陣理論的配電網運行狀態相關性分析方法[J]. 電網技術, 2016, 40(3): 781-790.

XU Xinyi, HE Xing, AI Qian, et al. A correlation analysis method for operation status of distribution network based on random matrix theory [J]. Power System Technology, 2016, 40(3): 781-790.

[19] 魏大千, 王 波, 劉滌塵, 等. 高維隨機矩陣描述下的量測大數據建模與異常數據檢測方法[J]． 中國電機工程學報，2015，35(s1)：59-66.

WEI Daqian, WANG Bo, LIU Dichen, et al. A method for WAMS big data modeling and abnormal data detection with large random matrices [J]. Proceedings of the CSEE，2015，35(s1.)：59-66.

[20] 嚴英杰, 盛戈皞, 王 輝, 等. 基于高維隨機矩陣大數據分析模型的輸變電設備關鍵性能評估方法[J]. 中國電機工程學報, 2015, 36(2): 435-445.

YAN Yingjie, SHENG Gehao, WANG Hui, et al. The key state assessment method of power transmission equipment using big data analyzing model based on large dimensional random matrix [J]. Proceedings of the CSEE，2015, 36(2): 435-445.

[21] 胡 江. 大維隨機矩陣經驗譜分布函數的收斂[D]. 長春: 東北師范大學, 2012.

HU Jiang. Convergence of empirical spectral distribution function for large dimensional random matrices[D]. Changchun: Northeast Normal University,2012.

[22] 曾杏元. 生成于四種流形上的大維隨機矩陣的譜分布[D]. 南京：中南大學, 2013.

ZENG Xinyuan. Spectral distribution of large dimensional random matrices generated on four manifolds[D]. Nanjing: Central South University,2013.

[23] GUIONNET A, KRISHNAPUR M, ZEITOUNI O. The single ring theorem [J]. Annals of Mathematics, 2011, 174(2): 1189-1217.

[24] FEINBERG J, SCALETTAR R, ZEE A. “Single ring theorem” and the disk-annulus phase transition [J]. Journal of Mathematical Physics, 2001, 42(12): 5718-5740.

[25] PETZ D, REFFY J. On asymptotics of large Haar distributed unitary matrices [J]. Periodica Mathematica Hungarica,2004,49(1):103-117.

[26] HE X, QIU R C , AI Q,et al. Designing for situation awareness of future power grids: an indicator system based on linear eigenvalue statistics of large random matrices [EB/OL]. IEEE Transactions on Smart Grid, 2016, DOI: 10.1109/ACCESS.2016.2581838.