橋梁應變監測數據中的溫度效應分析
楊海紅
(山西交通控股集團有限公司 運城南高速公路分公司,山西 運城 044000)
1 概述
橋梁健康監測中應變監測是最重要的監測內容,但由于橋梁結構受到復雜的溫度場影響,導致實測應變數據受溫度影響呈現較明顯的波動。事實上,橋梁結構除了受到車輛荷載作用之外,溫度也是較為重要的環境激勵。近年來,已有學者針對實測數據采用濾波的方法提取緩慢變化的溫度周期趨勢,從而將車輛荷載與溫度效應分離,為結構后續的安全監測及狀態評估提供參考。
但是針對溫度周期趨勢的研究仍有不足,由于車輛荷載對結構的運營的安全有著重要的影響,人們重點關注的是車輛荷載效應,而忽視了溫度效應。實際上結構實測應變的變化趨勢很大程度上與溫度有關,因此有必要對溫度效應進行深入研究。
本文依托風陵渡黃河大橋健康監測,該橋上部結構為預應變變截面連續梁,由主孔橋和邊孔橋組成。主孔橋跨徑組成為(87+7×114+87)m,邊孔橋跨徑組成為5×87 m。選擇主孔橋第13跨跨中下緣應變及相應的溫度測點。
2 實測應變的變化規律
風陵渡黃河大橋健康監測系統自2010年運行至今已將近8年,積累了大量的實測數據。雖然傳感器已經進行了溫度系數標定,但由于橋梁現場與實驗室的環境存在著很大的不同,因此,采用多年的實測應變和溫度數據進行回歸分析,并在此基礎上對應變傳感器進行溫度修正,盡量剔除溫度的影響。
應變監測的采樣頻率為3 min采集一次,由此造成全年的數據非常龐大,每個傳感器全年有17萬多條數據,由此使得后期處理相對較難。通過對數據進行認真分析,每天應變數據是隨著日照溫差的波動而周期變化,清晨是一天中箱梁內外溫差最小的時段。因此選擇每天清晨5:00時刻的應變測試數據進行分析。首先提取每天5:00~6:00范圍內實測數據,取其平均值作為當天應變及溫度測試結果代表值。通過繪制應變溫度曲線圖,發現其與溫度之間具有較好的線性相關,經回歸分析,可決系數R2接近于1,溫度與應變回歸分析見圖1。
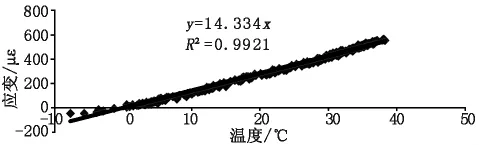
圖1 應變溫度回歸分析
在進行回歸分析過程中,應變和溫度均換算為相對變化量,回歸方程中的截距也相應為零,便可得到應變溫度的回歸系數。按照上述方法對歷年的監測數據進行回歸分析,結果如表1所示。
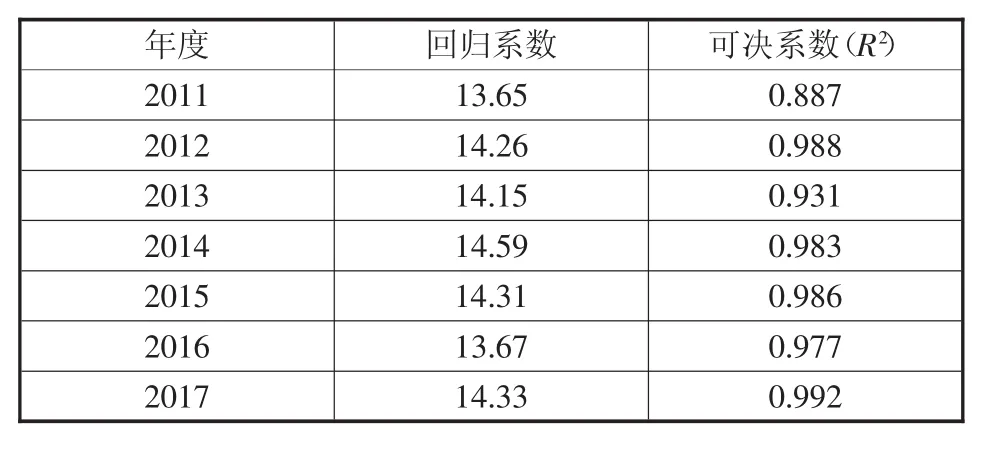
表1 歷年溫度回歸系數表
從表1可看出,歷年溫度回歸系數偏差不大,可決系數均接近于1,采用歷年回歸系數的平均值對實測應變進行溫度修正,修正后的2018年8月實測曲線見圖2。
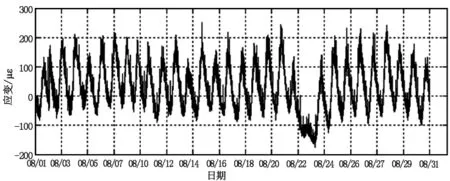
圖2 2018年8月實測應變曲線圖
從圖2可以看出,雖然采用歷年的溫度回歸系數對實測應變進行了溫度修正,但應變實測曲線仍然每天隨溫度產生較大的波動。應變曲線中存在著大量的毛刺,而這些毛刺是由車輛荷載產生的[1]。
由此,本文針對實測應變數據的變化規律,結合相應的溫度測試結果,對實測數據中的溫度效應進行分析。
3 實測應變的溫度效應分析
3.1 實測應變的平滑處理
從圖2可看出,實測應變受車輛荷載影響曲線并不光滑,因此,首先采用小波分析的方法將車輛荷載分離出來,從而得出光滑的僅受溫度影響的應變曲線見圖3。
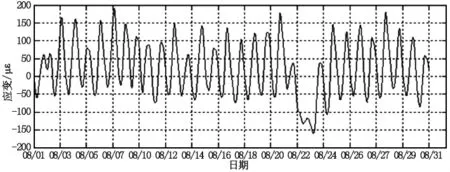
圖3 小波分析后的應變曲線圖
3.2 溫度滯后的處理
對溫度測試數據進行分析,溫度變化曲線如圖4所示。
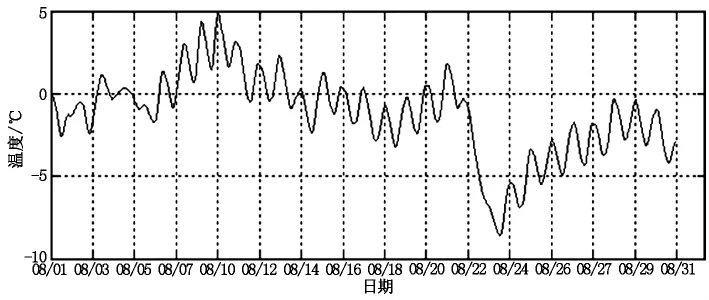
圖4 溫度變化曲線圖
對比圖3與圖4可以看出,應變與溫度變化規律基本一致,二者存在明顯的相關關系,同時相對應變而言,實測溫度有一定的滯后,這是由于測試的為箱內溫度,相對密封的箱梁結構導致箱內溫度與大氣溫度進行熱交換慢于結構的導熱過程。在數據處理過程中,對溫度數據進行平移,從而建立二者的真正對應關系。
3.3 多段溫度回歸模型
經上述分析之后,直接對溫度與應變進行回歸分析,結果發現二者完全沒有相關關系,曲線擬合較差。考慮到二者曲線形態較相近,因此,將曲線進行分段,分別進行溫度回歸[2]。首先根據曲線變化規律,尋找相應的特征點,采用特征點將曲線分隔為若干段,總共劃分57段曲線,對每段曲線進行回歸分析。
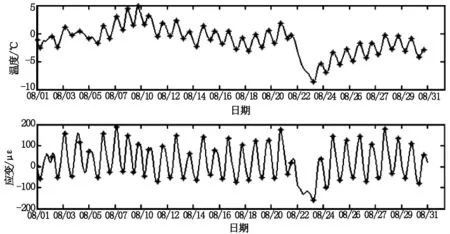
圖5 利用曲線特征點進行分段
通過對每段曲線進行回歸分析,僅有兩段曲線的可決系數在0.5~0.6之間,其余所有曲線的可決系數在0.89~0.99之間,說明二者具有較好的擬合優度。圖6為其中一段曲線的擬合結果。
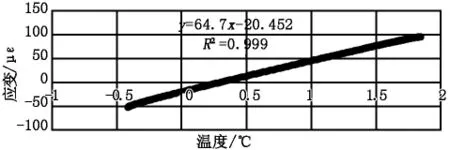
圖6 應變溫度回歸分析
從分段曲線來看,應變與溫度之間有著較強的線性回歸關系,但當總體進行回歸卻沒有這種規律,說明每段曲線其相應的回歸系數各不相同。為了能夠總體把握溫度與應變的相互關系,需要對每段曲線的回歸系數進行分析,尋找其相應的規律,選擇每段溫度的平均值、相對值(最大值與最小值的差值)作為自變量,每段曲線的回歸系數作為因變量進行回歸分析。
經多次組合分析,發現截距(即擬合公式中的b)與平均值之間有著較強的線性關系,而溫度系數(即擬合公式中的a)與相對值之間存在一定的指數關系,回歸分析見圖7和圖8。
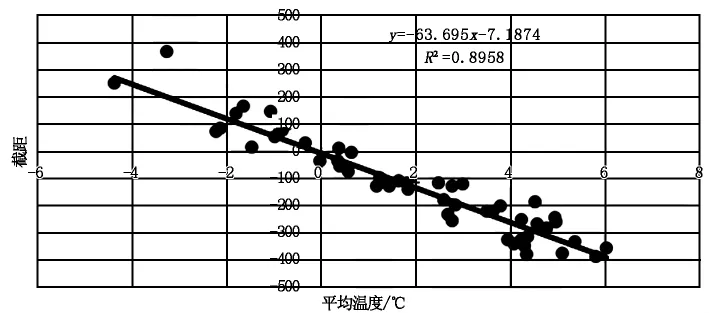
圖7 截距與平均溫度的回歸分析
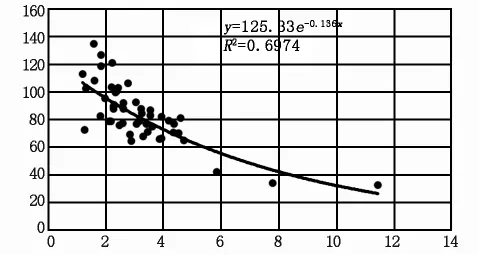
圖8 斜率與溫差的回歸分析
3.4 利用溫度回歸公式進行應變預測
采用上述方法便可得到溫度與應變回歸的一般公式為:
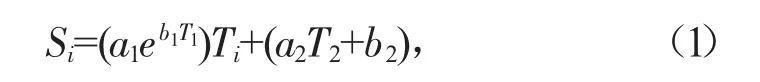
式中:Si為某時刻的應變;Ti為當前時刻的溫度;T1為當前溫度段的最大溫差;T2為當前溫度段的平均溫度;a1、b1、a2、b2分別為回歸系數。
按照上述方法對溫度進行分段平移之后,便可按照式(1)進行計算。然而在每段的分割點處,由于該點兩側的回歸公式計算結果不同,導致在該點出現臺階式的突變。導致曲線不連續,為了解決這個問題,經多次調整試算,采用以下辦法對計算應變進行修正:
a)首先分別根據該點兩側回歸公式的置信區間計算相應的置信度。
b)如果兩側的置信度較為接近,則該點的應變值為兩側計算結果的平均值,并以此結果對該點兩側的回歸公式進行修正,重新計算這兩段的應變值。
c)如果兩側的置信度相差較大,則選用置信度較大一側的計算結果作為該點的應變值,并以此為依據對置信度較小一側的計算結果進行修正。
按照上述方法計算結果見圖9,計算殘差均值為5.38με,說明多段回歸是能夠滿足工程實際需要的。
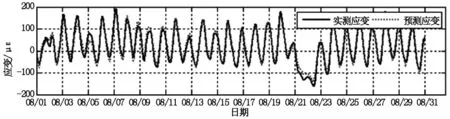
圖9 修正后的應變計算結果
4 結論
a)應變與溫度之間存在著線性相關關系,但不同時間段內,二者的相關系數不同,采用分段的溫度回歸模型能夠獲得較好的擬合優度。
b)每段應變回歸模型中,曲線斜率與該段時間的溫差存在相關關系,若采用線性回歸時,溫差較大時會導致出現負值,而采用指數擬合,溫差越大其變化率也相應較慢,更符合實際情況。
c)每段曲線的截距與該段時間的平均溫度存在較強的線性負相關。
d)應變與溫度的多段回歸模型也可應用于主梁撓度等其他參數,可在此基礎上對橋梁進行荷載識別與安全評估。

