初探GGB軟件在七年級數(shù)學動點問題中的應用

郭藝匯

【摘要】? 初一數(shù)學教學中，動點問題一直是難點問題，它不僅僅考察幾何推理能力和代數(shù)運算能力，還蘊含了初一學生很難掌握的分類討論思想，數(shù)形結(jié)合思想和整體思想，而GGB數(shù)學軟件有獨特的代數(shù)區(qū)和繪圖區(qū)，讓數(shù)形結(jié)合更直接生動;手動播放和重復播放功能，讓動靜結(jié)合，更有助于幫助學生掌握分類討論;平板操作，又有助于現(xiàn)場改編，一題多變，有助于幫助學生知識遷移;從而適當?shù)氖褂肎GB軟件，不僅僅提高老師的課堂效率，也能提高學生解決“定值問題”的綜合能力。

【關鍵詞】? GGB軟件 動點 數(shù)學思想 變式

【中圖分類號】? G633.6? ?? ? ? ? ?【文獻標識碼】? A ? ? 【文章編號】? 1992-7711（2018）12-165-02

0

初一上學期，我們初步學過當點動引起的線段長度的變化，角內(nèi)部射線動引起的角度的變化等，而本學期在學習平行線的性質(zhì)和判定以及平面直角坐標系之后，“動點問題”的綜合性更強，主要類型有：點動帶動的圖形的面積關系，某兩個或者某三個角之間的定值關系，平面直角坐標系中某動點的橫縱坐標關系等等;本文在《在平板上利用GGB軟件探究動態(tài)幾何問題》課題組研究的基礎上，以公開課《初一數(shù)學動點問題》中的片段為例，簡述利用GGB軟件在解決數(shù)學動點問題中的應用。

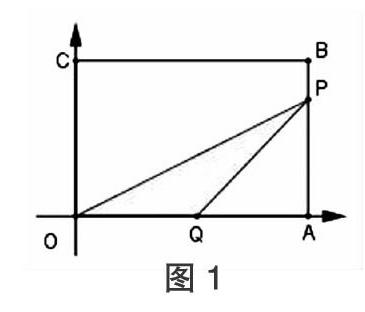
例題模型：在長方形OABC中，OA=6，OC=4，點P是AB邊上的點，AP=3，以點O為原點，以OA所在直線為x軸，OC所在直線為y軸，建立如圖所示的平面直角坐標系。

（1）點B的坐標是;

（2）若點Q從原點O出發(fā)，以每秒2個單位長度的速度沿著0→A→B→C的路線運動，當點Q運動到點C時停止運動，設運動時間為t;在點Q的運動過程中，是否存在某個時刻使得S△OPQ=6成立，若存在，求t的值，若不存在，說明理由;

一、代數(shù)繪圖，便于猜想，提煉數(shù)形結(jié)合

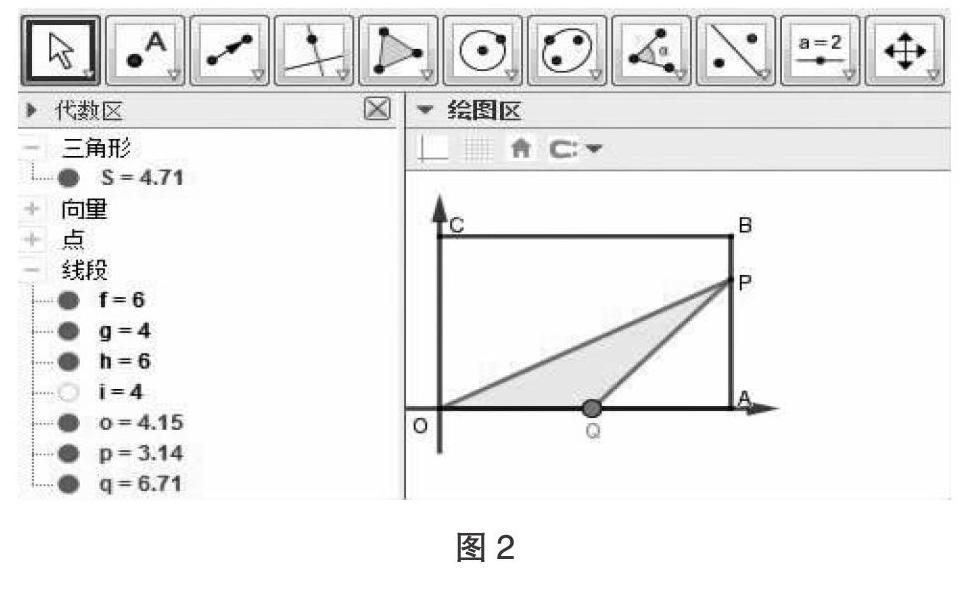
由于GGB軟件分有代數(shù)區(qū)和繪圖區(qū)，使數(shù)形結(jié)合更直觀，繪圖區(qū)的圖形在變，代數(shù)區(qū)的數(shù)據(jù)就是跟隨變化，這一獨特優(yōu)勢，只要代數(shù)區(qū)內(nèi)的數(shù)據(jù)拖入繪圖區(qū)，便可清晰觀察到在運動變化過程中，各個量的具體數(shù)據(jù).有助于幫助學生猜想并驗證，既能提高學生的興趣，也能提升其分析動點問題的能力。如在解答問題（2）時，慢速拖動點Q（如圖1），在繪圖區(qū)中，當點Q沿著沿著0→A→B→C的路線的運動過程中，在代數(shù)區(qū)可以發(fā)現(xiàn)有三個瞬間也就是三個時刻滿足S△OPQ=6，很容易引導學生猜想這個問題需要分類討論，而且有三個答案。

二、手動播放，便于分類，提煉分類討論

GGB軟件中動點的手動播放功能，動靜可控，既可以宏觀觀察由點動帶來的線動以及圖形的變化，也可以在臨界點停止，幫助學生發(fā)現(xiàn)臨界狀態(tài)的臨界數(shù)據(jù)，特別適宜用在初一分類談論這一難點的教學活動中。以問題（2）為例，學生很容易理解此類問題轉(zhuǎn)化為方程問題，就是把S△OPQ用時間t的式子表示即可，可是由于△OPQ的不確定性，學生很難不重不漏的把所有情況考慮到，而即使教師將完整的情況分析完整并板書到位，下次遇到此類題稍微改動下運動軌跡，學生就又考慮不全面了，GGB軟件中動點的手動播放功能，在以下幾個步驟中可發(fā)揮其獨特的優(yōu)勢：

1.“繪圖區(qū)”可清晰展示△OPQ的三種位置變化，“手動播放”功能使動點隨動隨停，可以幫助學生在頭腦中清晰的把動點定格，從而不確定的圖形位置瞬間形象具體，幾乎所有的學生能理解到本題分三種情況討論，并且三種情況下的圖形一目了然，對應列方程求解即可，有利于掌握分類討論思想。

2.“代數(shù)區(qū)”里面的“點”“線段”“面積”等分別顯示出不同情況下點的坐標，線段的長度以及圖形的面積，代數(shù)區(qū)和繪圖區(qū)結(jié)合，有助于幫助學生制定分類討論的具體數(shù)據(jù).

繪圖區(qū)出現(xiàn)的三個臨界狀態(tài)分別為點Q與點A重合時（如圖3），點Q與點B重合時，點Q與點C重合，而此時代數(shù)區(qū)分別對應為t=3，t=5，t=8的標準數(shù)據(jù)，從而可知本題可分為以下三個分段：①0≤t<3時，②3≤t<5時，③5≤t<8對應圖形為如下圖（1-3）.

3.“重復播放”可以讓動畫可以任意回放，教師可以輕松依據(jù)圖形引導學生注意標準要“不重不漏”以及利用第10章《數(shù)據(jù)統(tǒng)計與分析》中分組標準，臨界數(shù)據(jù)t=3，5，8所在分組的分析和解釋。

三、重復播放，便于驗證，提煉整體思想

GGB軟件的重復播放功能，便于分析計算并驗證.GGB軟件的手動播放和重復播放功能，可以隨停隨動，所以可以分別將將動畫定格于圖3、圖4、圖5位置加以分析.啟用平板或投影上的畫筆功能，在相應的底和高上標上對應的長，這時，準確求出S△OPQ的表達式這一難點就被簡化為簡單的整式計算了，最后列方程求出t的值。

四、平板操作，便于改編，提煉變式遷移

單動點改為雙動點的變式1：若有兩動點P，Q同時出發(fā)，P點從C點出發(fā)沿y軸負方向以每秒2個單位長度的速度勻速移動.Q點從O點出發(fā)以每秒3個單位長度的速度沿O→A→B→C的路線移動，點Q到達C點整個運動隨之結(jié)束.點D的坐標是（3，2），設運動時間為t秒。問：是否存在這樣的t，使S△ODP=S△OPQ？若存在，請求出t的值;若不存在，請說明理由

學生用平板自主播放動畫，按圖6——圖9三種情況分小組完成后，教師用平板將學生的答題情況拍照后，投影到屏幕，加以對比點評。

為了調(diào)動學生的學習興趣，可以繼續(xù)現(xiàn)場改編為如下4種變式訓練，讓學生體會并掌握解決動點問題的本質(zhì)，提高教學效率，提升教學成果。

雙動點面積定值問題變式2：如圖，若有兩動點P，Q同時出發(fā)，點P從C點出發(fā)，以每秒2個單位長度的速度向CB方向勻速運動（不超過點B），點Q從B點出發(fā)，以每秒1個單位長度向BA方向勻速運動（不超過點A），在點P、Q運動過程中，四邊形PBQO的面積是否發(fā)生變化？若不變，求其值;若變化，求其變化范圍。

角度問題改為橫縱坐標關系問題變式5：點M是線段AC上一動點，點M的坐標為（m，n）在點M運動過程中，m，n滿足的關系式。

總之，在數(shù)學教學中運用GGB軟件進行動態(tài)演示，獨特的功能不僅幫助學生準確分類討論，不重不漏解決動點帶來的不確定性，更可以高效快速進行變式訓練，對提高初一學生的數(shù)學思維能力和解題能力大有幫助，還能培養(yǎng)學生深入研究數(shù)學問題學習習慣。

[ 參? 考? 文? 獻 ]

[1]基于GeoGebra的數(shù)學教學全過程優(yōu)化研究[J].左曉明，田艷麗，贠超.數(shù)學教育學報.

[2]張慶臣，陳維君.一題多變提升學生的創(chuàng)新思維能力[J].中國數(shù)學教育（初中版），2009（4）：25-28.

[3]肖川.義務教育數(shù)學課程標準解讀[M].湖北教育出版社，2011.