基于動(dòng)態(tài)DCVS網(wǎng)絡(luò)模型的流量分析及規(guī)劃方法*

吳 博，王 彬，薛 潔，劉 輝，熊 新

(1．昆明理工大學(xué)信息工程與自動(dòng)化學(xué)院，云南昆明650504;2．云南警官學(xué)院信息網(wǎng)絡(luò)安全學(xué)院，云南昆明650223)

1 引言

面對(duì)機(jī)場(chǎng)日益增加的行李運(yùn)輸量，建立實(shí)時(shí)高效的機(jī)場(chǎng)行李處理系統(tǒng)BHS(Bagage Handing System)變得尤為重要。在整個(gè)機(jī)場(chǎng)行李處理系統(tǒng)中，負(fù)責(zé)國(guó)內(nèi)航線運(yùn)輸?shù)膰?guó)內(nèi)航站樓(Domestic Terminal)和負(fù)責(zé)國(guó)外航線運(yùn)輸?shù)膰?guó)際航站樓(International Terminal)之間通常距離較長(zhǎng)，這種不同航站樓之間的行李運(yùn)輸稱為遠(yuǎn)端行李運(yùn)輸。遠(yuǎn)端行李運(yùn)輸系統(tǒng)是整個(gè)BHS的關(guān)鍵組成部分，傳統(tǒng)的遠(yuǎn)端行李運(yùn)輸系統(tǒng)一般采用人工車輛運(yùn)輸?shù)姆椒ǎ壳埃S著機(jī)場(chǎng)需求的提高和技術(shù)的發(fā)展，越來越多的國(guó)際大型樞紐機(jī)場(chǎng)采用目的地編碼車系統(tǒng)DCVS(Destination Coded Vehicle System)解決遠(yuǎn)端行李的輸送問題［1-8］。DCVS由若干輛DCV小車、封閉的軌道系統(tǒng)、控制系統(tǒng)和小車調(diào)度管理系統(tǒng)等組成，系統(tǒng)使用目的地編碼認(rèn)址技術(shù)對(duì)DCV小車進(jìn)行控制，并且可以與BHS中的行李分揀系統(tǒng)直接無縫集成在一起。與原有的BHS控制構(gòu)架相比較，DCVS真正實(shí)現(xiàn)了機(jī)場(chǎng)行李處理系統(tǒng)的自動(dòng)化控制和運(yùn)行，并且極大地提高了機(jī)場(chǎng)行李處理系統(tǒng)的整體運(yùn)行效率［9-12］。

保障DCVS高速運(yùn)行的關(guān)鍵是合理的流量規(guī)劃及有效的實(shí)時(shí)狀態(tài)監(jiān)控，但是遠(yuǎn)端行李運(yùn)輸?shù)穆烦梯^遠(yuǎn)，軌道設(shè)計(jì)較為復(fù)雜，尤其是在軌道上同時(shí)運(yùn)行的DCV小車數(shù)量眾多，通常都是平均每分鐘數(shù)百臺(tái)，這些特點(diǎn)給DCVS的流量分析、路徑規(guī)劃和運(yùn)行狀態(tài)監(jiān)控帶來了困難。目前已采用DCVS的機(jī)場(chǎng)的路徑規(guī)劃方法都是提前固定好起點(diǎn)到終點(diǎn)的路徑，即DCV按照既定的靜態(tài)規(guī)劃方式運(yùn)行，此外不管實(shí)際流量的需求怎樣，DCVS的資源都是一直全部在使用中的。這種規(guī)劃方法由于不考慮系統(tǒng)的實(shí)時(shí)狀態(tài)信息而缺乏靈活性，很容易造成資源的浪費(fèi)，并可能因?yàn)樾欣顭o法在規(guī)定的時(shí)間窗口內(nèi)運(yùn)達(dá)終點(diǎn)而影響整個(gè)BHS的正常運(yùn)行，給旅客帶來不便，同時(shí)給機(jī)場(chǎng)運(yùn)營(yíng)造成經(jīng)濟(jì)損失。

由于DCVS出現(xiàn)的時(shí)間較短，所以相關(guān)研究文獻(xiàn)較少，但是隨著DCVS投入使用數(shù)量的增加以及現(xiàn)有流量規(guī)劃和控制方法所顯現(xiàn)出的弊端，已經(jīng)有研究者開始關(guān)注該領(lǐng)域并對(duì)DCVS的控制和路徑規(guī)劃問題展開了研究。荷蘭Delft理工大學(xué)的Tarau等人［13］于2008年針對(duì)DCVS建立了基于事件的驅(qū)動(dòng)模型，用多種傳統(tǒng)控制方法對(duì)DCV運(yùn)行時(shí)間展開了研究，實(shí)驗(yàn)表明隨著行李數(shù)量增加，計(jì)算時(shí)間呈指數(shù)倍增長(zhǎng)。2009年，Tarau等人［14］分別使用集中式路徑選擇控制方法和分散式路徑選擇控制方法對(duì)DCVS的路徑規(guī)劃進(jìn)行了對(duì)比研究。結(jié)果表明，集中控制在路徑規(guī)劃的分配上占優(yōu)，分散式控制在整體計(jì)算時(shí)間上占優(yōu)。2009年，Tarau等人［15］針對(duì)在集中控制下計(jì)算時(shí)間長(zhǎng)的缺陷，分別使用分布式模型預(yù)測(cè)控制和分布式啟發(fā)控制對(duì)計(jì)算時(shí)間進(jìn)行了優(yōu)化，結(jié)果表明兩種方法的結(jié)合可以在文獻(xiàn)［13］的基礎(chǔ)上減少百分之二十的運(yùn)算時(shí)間，但隨著行李數(shù)量增多，其運(yùn)算時(shí)間的大量增加仍然不可避免。2009年，Tarau等人［16］為了達(dá)到計(jì)算時(shí)間與控制最優(yōu)的目的，提出了集中啟發(fā)式控制的策略并用于DCV路徑規(guī)劃的研究上。實(shí)驗(yàn)表明，該策略無論在計(jì)算時(shí)間上還是最優(yōu)規(guī)劃上都優(yōu)于文獻(xiàn)［13- 15］的方法。此外 Mao等人［17］針對(duì)DCV路徑規(guī)劃，加入不同路段的最大速度與加速度的約束考慮，建立了DCV最優(yōu)路徑規(guī)劃的時(shí)間模型，實(shí)驗(yàn)結(jié)果顯示該模型符合實(shí)際需求，可以為實(shí)際DCV路徑規(guī)劃提供參考。

上述工作從控制領(lǐng)域中經(jīng)典的優(yōu)化規(guī)劃控制方法出發(fā)，大都以單個(gè)DCV小車為對(duì)象展開研究，試圖對(duì)每一個(gè)小車運(yùn)行路徑進(jìn)行規(guī)劃，將問題映射為DCVS內(nèi)每一個(gè)個(gè)體的運(yùn)行時(shí)間和運(yùn)算時(shí)間的組合優(yōu)化問題來求解，從理論上給出了解決方案。但是，由于DCVS中同時(shí)運(yùn)行的DCV小車數(shù)量至少高達(dá)上百輛，這些路徑規(guī)劃方法所需的運(yùn)算時(shí)間無法滿足實(shí)際DCVS運(yùn)行中的實(shí)時(shí)性要求及流量需求。同時(shí)上述方法僅從系統(tǒng)的個(gè)體特性出發(fā)而沒有考慮整個(gè)系統(tǒng)的全局流量控制信息，并且忽略了DCV控制系統(tǒng)中的實(shí)時(shí)狀態(tài)信息。在實(shí)際系統(tǒng)運(yùn)行中，機(jī)場(chǎng)行李流、DCVS軌道系統(tǒng)和控制系統(tǒng)等信息在每個(gè)不同的采樣時(shí)刻都是實(shí)時(shí)變化的，因此有效地獲取DCV系統(tǒng)的實(shí)時(shí)運(yùn)行狀態(tài)和系統(tǒng)流量需求，并據(jù)此對(duì)DCV小車的運(yùn)行情況進(jìn)行整體動(dòng)態(tài)的規(guī)劃是提高DCVS乃至BHS效率的有效解決方案。

針對(duì)上述研究現(xiàn)狀，本文以滿足機(jī)場(chǎng)遠(yuǎn)端行李運(yùn)輸?shù)膶?shí)時(shí)流量需求為目標(biāo)，從DCV控制系統(tǒng)的動(dòng)態(tài)特性和全局角度出發(fā)研究DCVS的動(dòng)態(tài)流量規(guī)劃問題。研究首先基于圖論建立DCVS的靜態(tài)運(yùn)輸網(wǎng)絡(luò)模型，在此基礎(chǔ)上結(jié)合系統(tǒng)的實(shí)時(shí)流量需求變化給出了一種基于最大流最小時(shí)間的動(dòng)態(tài)DCVS流量規(guī)劃、預(yù)測(cè)和控制方法。該方法通過規(guī)劃源點(diǎn)所有DCV的整體路徑對(duì)來實(shí)現(xiàn)對(duì)DCVS運(yùn)輸軌道系統(tǒng)資源的最大化利用，并且可以對(duì)DCVS在特定時(shí)間區(qū)間內(nèi)所能完成運(yùn)輸任務(wù)的數(shù)量進(jìn)行預(yù)測(cè)和評(píng)估，從而為DCVS的實(shí)時(shí)流量控制提供依據(jù)。實(shí)驗(yàn)結(jié)果顯示，本文方法能夠在保證流量需求的前提下優(yōu)化DCV小車的運(yùn)行時(shí)間，并且優(yōu)化算法的運(yùn)算時(shí)間很短，有效提高了DCVS的工作效率和資源利用率，同時(shí)為保障和提高整個(gè)BHS的可控性和穩(wěn)定性提供了有效的解決方案。

2 基于圖論的DCVS靜態(tài)網(wǎng)絡(luò)模型構(gòu)建

2．1 DCVS物理模型描述

在實(shí)際DCVS中，機(jī)場(chǎng)行李處理系統(tǒng)是從行李通過值機(jī)柜臺(tái)后開始運(yùn)行的，根據(jù)不同的目的地，行李通過傳送帶被送往不同的終端，若識(shí)別到某行李需要進(jìn)行遠(yuǎn)端運(yùn)輸，那么該行李就會(huì)被傳送至DCVS的行李裝載站，空的DCV在行李裝載站等待行李，一旦在裝載站臺(tái)出現(xiàn)行李流，DCV就按照“一車一行李”的方式將行李進(jìn)行裝載并在DCVS中進(jìn)行運(yùn)輸［18-20］。如圖1所示，DCVS物理模型主要由三部分組成:裝載站L(如圖1a所示)、卸載站U(如圖1b所示)和DCVS運(yùn)輸軌道R(如圖1c所示)。假定有m個(gè)裝載站和n個(gè)卸載站，行李依照分揀系統(tǒng)中識(shí)別的優(yōu)先級(jí)別預(yù)先載入到DCV小車上，DCV通過運(yùn)輸軌道被送到卸載站。

2．2 基于圖論的DCVS靜態(tài)網(wǎng)絡(luò)模型構(gòu)建方法

根據(jù)上述DCVS物理模型，DCV在DCVS中的行為主要可分為在裝載站處裝載行李、在軌道系統(tǒng)中運(yùn)行和到目的地卸載站處卸下行李三種。在無故障的前提下，DCV可在系統(tǒng)中往返運(yùn)行，重復(fù)使用。由于DCV返回時(shí)有專門的返回線路，與行李的運(yùn)輸線路沒有任何沖突，因此在本文研究中忽略不考慮。可供使用的裝載站和卸載站的端口數(shù)量是固定的，但實(shí)際運(yùn)行的端口數(shù)量可根據(jù)實(shí)際流量需求的不同加以調(diào)整。基于以上分析，本文采用圖論的基本理論和網(wǎng)絡(luò)模型對(duì)圖1中的DCVS物理模型進(jìn)行建模和分析。首先把DCV系統(tǒng)定義為一個(gè)圖，系統(tǒng)中的站點(diǎn)，包括裝載站、卸載站和各個(gè)交叉站點(diǎn)定義為圖的節(jié)點(diǎn)，裝載站與站點(diǎn)之間、站點(diǎn)與站點(diǎn)之間、站點(diǎn)與卸載站之間的每一條路段定義為圖的邊。由此得到DCVS物理模型所對(duì)應(yīng)的靜態(tài)網(wǎng)絡(luò)模型，記為 G(V，L，U，E)，其中，V={B1，B2，B3，…，Bk}表示交叉站點(diǎn)集，k為交叉站點(diǎn)的個(gè)數(shù);L={l1，l2，l3，…，lM}表示裝載點(diǎn)站集，M 為裝載站點(diǎn)個(gè)數(shù);U={u1，u2，u3，…，uN}表示卸載站點(diǎn)集，N 為卸載站點(diǎn)個(gè)數(shù);E={e1，e2，e3，…，ej}表示所有路段的集合，其中j為路段的數(shù)量。

根據(jù)實(shí)際的機(jī)場(chǎng)DCVS的框架結(jié)構(gòu)，為了后文實(shí)驗(yàn)和研究需要，本文給出一個(gè)具體的DCVS的網(wǎng)絡(luò)模型，如圖2所示，該系統(tǒng)共有8個(gè)裝載站，4個(gè)卸載站可供使用。盡管實(shí)際運(yùn)行中的DCV系統(tǒng)會(huì)在規(guī)模和站點(diǎn)數(shù)量上有所不同，但在使用本文算法進(jìn)行流量的分析和規(guī)劃的目標(biāo)是，確定當(dāng)前系統(tǒng)配置是否可以滿足該時(shí)段的流量需求，因此本文方法對(duì)不同規(guī)模和站點(diǎn)數(shù)量均可適用。可得到該DCVS 的靜態(tài)網(wǎng)絡(luò)模型為 G(V，L，U，E)，L={l1，l2，l3，…，l8}，U={u1，u2，u3，u4}，E={e1，e2，e3，…，e32}。并且站點(diǎn)與站點(diǎn)之間是有權(quán)連接的，圖2中給出的權(quán)值是路段的長(zhǎng)度，單位是m。同時(shí)站點(diǎn)之間的權(quán)值還有流量、容量等屬性。

2．3 DCVS建模的約束條件分析

根據(jù)DCVS運(yùn)行中的實(shí)際情況，為后文研究需要，本文首先對(duì)基于圖論的DCVS建模過程中的一些物理約束作出如下假設(shè):

(1)在DCVS中，如果某裝載站點(diǎn)需處理的行李數(shù)量為Nbagage，該站點(diǎn)可供使用的DCV數(shù)量為NDCV。那么規(guī)定Nbagage≤ NDCV，即不會(huì)因起點(diǎn)處沒有DCV小車而耽誤繼續(xù)運(yùn)輸行李。

(2)在起點(diǎn)處，假設(shè)共有X個(gè)行李需要被送往對(duì)應(yīng)的遠(yuǎn)端目的地，共開放M個(gè)裝載站對(duì)這X個(gè)行李進(jìn)行處理，其中bmax為每個(gè)裝載站的最大裝載量。那么規(guī)定這X個(gè)行李按照F=X/M(L表示每個(gè)裝載站可處理行李的數(shù)量)分配給每個(gè)裝載站，并且滿足X≤Fbmax。

(3)在卸載站點(diǎn)處，可對(duì)早到行李進(jìn)行存儲(chǔ)，若早到行李過多就會(huì)由于存儲(chǔ)力不夠而導(dǎo)致容量溢出。如果用Y表示終點(diǎn)的行李個(gè)數(shù)，各個(gè)卸載站點(diǎn)的最大存儲(chǔ)能力為dmax。假定有N個(gè)可用的卸載站點(diǎn)，那么規(guī)定這Y個(gè)行李按照Q=Y/N(Q表示每個(gè)卸載站可存儲(chǔ)行李的數(shù)量)分配給每個(gè)卸載站，且滿足Y≤Qdmax。

(4)實(shí)際運(yùn)行軌道可能由直線軌道、彎曲軌道、合流軌道、分流軌道以及傾斜15度坡軌道等組成［21］。DCV小車在實(shí)際中會(huì)因路段和邏輯區(qū)域不同而運(yùn)行在幾種速度級(jí)別上，在目前的研究中，由于采取整體流量規(guī)劃的策略，因此考慮的是DCV在整個(gè)軌道網(wǎng)絡(luò)上的平均運(yùn)輸速度，并且假定每一個(gè)DCV的運(yùn)行速度相同。

(5)車輛在某一段軌道上運(yùn)行時(shí)，如果遇到本路段的擁堵或故障等問題，DCV在原位置等待系統(tǒng)恢復(fù)正常再繼續(xù)運(yùn)行，即除了單獨(dú)的返回路段以外，DCV在每一路段上單向運(yùn)行，不可后退到上一級(jí)站點(diǎn)重新選擇路徑。

(6)目前研究中暫未考慮多個(gè)DCV流過同一分流站點(diǎn)時(shí)的路由選擇，以下文算法中規(guī)劃的各個(gè)路段流量為依據(jù)，按照先進(jìn)先通過的原則通過每一個(gè)交叉站點(diǎn)。

(7)在機(jī)場(chǎng)的行李運(yùn)輸系統(tǒng)中，因?yàn)閷?shí)際的航班運(yùn)行情況和時(shí)間窗口要求會(huì)產(chǎn)生行李的運(yùn)輸優(yōu)先級(jí)別不同，該問題一般由BHS中的行李分揀部分來分析解決，對(duì)于本文所研究的DCV遠(yuǎn)端運(yùn)輸系統(tǒng)，行李的優(yōu)先級(jí)別問題已經(jīng)通過進(jìn)入裝載站時(shí)的排隊(duì)先后而解決，因此在運(yùn)輸過程中無需再考慮行李優(yōu)先級(jí)別問題。

3 基于流量分析的DCVS動(dòng)態(tài)網(wǎng)絡(luò)模型構(gòu)建方法

3．1 基于流量分析的DCVS動(dòng)態(tài)網(wǎng)絡(luò)模型思想

盡管在圖1所示的DCVS靜態(tài)網(wǎng)絡(luò)模型中，已經(jīng)得到 DCVS的基本結(jié)構(gòu)，但是該模型只能對(duì)DCVS進(jìn)行靜態(tài)屬性的描述，比如站點(diǎn)之間的連接關(guān)系，路段的容量、流量、距離等。但是，在DCVS的實(shí)際運(yùn)行過程中，由于每一時(shí)段實(shí)際DCVS的系統(tǒng)流量需求可能不同，可用的行李裝載站點(diǎn)和行李卸載站點(diǎn)的開放數(shù)量可能不同，實(shí)際DCV所選擇的路徑可能不同，因此該模型結(jié)構(gòu)及屬性并非靜止不變的，而是隨時(shí)可能發(fā)生變化，因此只根據(jù)第2．1節(jié)中的模型還不足以描述DCVS的動(dòng)態(tài)特征。

文獻(xiàn)［13-16］中的研究和實(shí)驗(yàn)結(jié)果顯示:以單個(gè)DCV小車作為規(guī)劃對(duì)象的最優(yōu)化時(shí)間算法費(fèi)時(shí)太長(zhǎng)，尤其在行李數(shù)目增加時(shí)，其運(yùn)算時(shí)間幾乎呈指數(shù)級(jí)增長(zhǎng)，無法滿足DCV控制系統(tǒng)的實(shí)際運(yùn)行時(shí)間要求。而整個(gè)DCVS運(yùn)行的最主要目標(biāo)是行李流必須在指定的時(shí)間內(nèi)運(yùn)抵遠(yuǎn)端目的地，因此本文以滿足DCVS的流量需求為目標(biāo)，采用整體流量和路徑規(guī)劃的思想，構(gòu)建DCV系統(tǒng)的動(dòng)態(tài)網(wǎng)絡(luò)模型，并在該動(dòng)態(tài)模型的基礎(chǔ)上對(duì)DCVS的流量控制和路徑控制問題展開研究。該方法的基本思想是:以每個(gè)統(tǒng)計(jì)時(shí)間區(qū)間上的實(shí)際流量需求信息為依據(jù)，采用最短時(shí)間最大流算法與超級(jí)源點(diǎn)和超級(jí)匯點(diǎn)相結(jié)合的算法預(yù)測(cè)整個(gè)系統(tǒng)可達(dá)到的最大流量，用于評(píng)估在規(guī)定時(shí)間窗內(nèi)，當(dāng)前的可用資源能否滿足系統(tǒng)的需求，從而有效地利用和分配資源;同時(shí)，可以有效地掌握當(dāng)前時(shí)刻每條路段上所運(yùn)行的DCV小車的最佳流量分配方案，這樣不但可以保證計(jì)劃的行李流能夠在規(guī)定時(shí)間內(nèi)到達(dá)遠(yuǎn)端目的地，同時(shí)也可準(zhǔn)確地掌握DCVS控制系統(tǒng)的實(shí)時(shí)信息。

3．2 流量需求分析

DCVS流量規(guī)劃需滿足以下條件:(1)在每個(gè)時(shí)間區(qū)間上滿足行李流的總需求;(2)總的行李流必須在規(guī)定的時(shí)間窗內(nèi)到達(dá)卸載站;(3)每條路段上的DCV流量在容量允許范圍內(nèi)。根據(jù)機(jī)場(chǎng)的實(shí)際行李流信息、機(jī)場(chǎng)遠(yuǎn)端行李處理過程中的行李處理要求與規(guī)定以及行李到達(dá)時(shí)間安排等數(shù)據(jù)綜合考慮，可以得到每個(gè)時(shí)間區(qū)間上的行李流信息，其中包括實(shí)際中轉(zhuǎn)行李需求、當(dāng)前提供的裝載站數(shù)量、當(dāng)前提供的卸載站數(shù)量等。表1給出了其中四個(gè)不同時(shí)間區(qū)間上的遠(yuǎn)端行李處理需求信息數(shù)據(jù)。

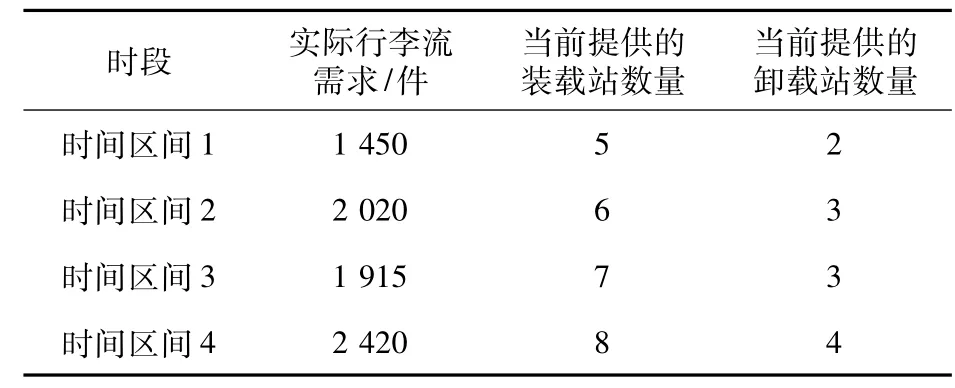
Table 1 Data of different sampling intervals表1 不同采樣時(shí)刻區(qū)間的數(shù)據(jù)

以時(shí)間區(qū)間1為例，此時(shí)段系統(tǒng)中一共有待遠(yuǎn)端運(yùn)輸?shù)男欣? 450件，即對(duì)DCV的需求是1 450車次。時(shí)間區(qū)間1內(nèi)的所有行李都需要在規(guī)定的時(shí)間窗口內(nèi)完成從裝載站到卸載站的運(yùn)輸，目前可供使用的裝載站數(shù)量為8，實(shí)際在用的裝載站數(shù)量為5，可供使用的的卸載站數(shù)量為4，實(shí)際在用的卸載站數(shù)量為2。

3．3 基于最大流最短時(shí)間原理的DCVS動(dòng)態(tài)流量規(guī)劃算法的實(shí)現(xiàn)

由于一般的最大流算法只適用于單源單匯情況下的流量分析，而在DCVS中，一般都是要同時(shí)開放多個(gè)裝載站點(diǎn)和卸載站點(diǎn)，因此單源單匯算法不足以解決DCVS的實(shí)際流量分析問題。因此，本文首先為DCVS靜態(tài)模型加入超級(jí)源點(diǎn)與超級(jí)匯點(diǎn)，如圖3所示。在圖3中，構(gòu)建超級(jí)源點(diǎn)S與各個(gè)裝載站相連接，超級(jí)匯點(diǎn)T與各個(gè)卸載站相連接。圖3中路段上括號(hào)內(nèi)的第一個(gè)權(quán)值為該路段的距離，第二個(gè)權(quán)值為該路段最大可容納的DCV流量(下文簡(jiǎn)稱容量)，第三個(gè)權(quán)值為經(jīng)過該路段所需要花費(fèi)的時(shí)間(下文簡(jiǎn)稱時(shí)間)。因?yàn)榕c超級(jí)源點(diǎn)、超級(jí)匯點(diǎn)連接的路段在實(shí)際中是不存在的，所以與超級(jí)站點(diǎn)相連路段中的第一個(gè)權(quán)值與第三個(gè)權(quán)值是不存在的，即為0，但是該路段上的容量權(quán)值是存在的。對(duì)于裝載站而言，從超級(jí)源點(diǎn)到各個(gè)裝載站的流方向?yàn)榱魅耄鶕?jù)流的平衡條件，即流入超級(jí)節(jié)點(diǎn)的流量等于流出超級(jí)節(jié)點(diǎn)的流量法則可知，該段上的容量應(yīng)該等于從該裝載站點(diǎn)流出的流量之和。同理，對(duì)于卸載站而言，從各個(gè)卸載站到超級(jí)匯點(diǎn)的流方向?yàn)榱鞒觯摱紊系娜萘繎?yīng)該等于流入該裝載站的流量之和。

接下來利用最短時(shí)間最大流算法對(duì)圖3所示的模型進(jìn)行動(dòng)態(tài)流量規(guī)劃，具體規(guī)劃方法(如圖4所示)如下:

(1)輸入圖3所示的加入超級(jí)源點(diǎn)和超級(jí)匯點(diǎn)后的網(wǎng)絡(luò)G，任意找到一條初始可行流，并確定該初始可行流f(k)=0，此時(shí)k=0。

(2)記f(k)為經(jīng)過k次調(diào)整得到的最小時(shí)間費(fèi)用流，構(gòu)建對(duì)應(yīng)的有向圖網(wǎng)絡(luò)W(f(k))。

(3)利用Dijkstra算法求出W(f(k))中從S到T的最短路R(k)，若R(k)不存在，則f(k)是最小時(shí)間最大流，轉(zhuǎn)向(5);否則，轉(zhuǎn)向(4)。

(4)在W(f(k))中找到對(duì)應(yīng)的增廣鏈μ，在增廣鏈μ上對(duì)f(k)按式(1)進(jìn)行流量調(diào)整，得到新的可行流f(k+1)，此時(shí)令k=k+1，轉(zhuǎn)入(2)。

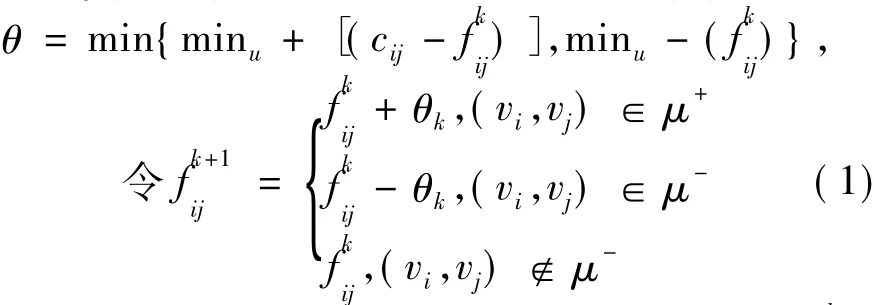
其中，cij表示從起點(diǎn)i到終點(diǎn)j路段上的容量表示第k次構(gòu)建的可行流fij，θk表示第k次的調(diào)整量，u+表示正向弧集合，u－表示反向弧集合。

(5)停止運(yùn)算，并輸出當(dāng)前最小時(shí)間可行流f(k)，作為G的最小時(shí)間最大流。

本文采用Linear Interactive and General Optimizer(以下簡(jiǎn)稱Lingo)平臺(tái)實(shí)現(xiàn)上述算法的仿真。Lingo是一套專門用于求解最優(yōu)化問題的軟件包，它由美國(guó)芝加哥大學(xué)的Linus Schrage開發(fā)［22］。該軟件既可用于求解線性規(guī)劃問題，還可以用于解決非線性規(guī)劃問題。如圖5所示，以表1中的時(shí)間區(qū)間4為例，在當(dāng)前開啟8個(gè)裝載站、4個(gè)卸載站時(shí)，經(jīng)過Lingo計(jì)算得出:可提供的DCV運(yùn)輸次數(shù)，即圖5a中的Objective value是2 485次，計(jì)算該數(shù)據(jù)并規(guī)劃出相對(duì)應(yīng)的流量分配的計(jì)算時(shí)間僅需0．07 s，該算法可在極短時(shí)間內(nèi)運(yùn)算得到當(dāng)前系統(tǒng)資源配置下特定時(shí)間區(qū)間4上的實(shí)際最大行李流，從而可為DCV系統(tǒng)的實(shí)時(shí)規(guī)劃和控制提供有力支持。

我們對(duì)當(dāng)前動(dòng)態(tài)規(guī)劃結(jié)果中的所有路段依次進(jìn)行標(biāo)號(hào)，標(biāo)號(hào)結(jié)果為1～61，將該算法規(guī)劃后的各個(gè)路段上流量分配情況與靜態(tài)時(shí)路段的容量通過柱狀圖進(jìn)行對(duì)比，可以得到圖5b。由圖5b中可以直觀地觀測(cè)到當(dāng)前的實(shí)際流量分配以及容量與流量的差別。

控制時(shí)段4規(guī)劃后的動(dòng)態(tài)模型如圖6所示。由于超級(jí)源點(diǎn)S、匯點(diǎn)T的構(gòu)建作用是為了進(jìn)行流量的整體規(guī)劃而加入的，因此在完成動(dòng)態(tài)規(guī)劃后，刪除S、T，從而可以得到最終的DCV軌道系統(tǒng)動(dòng)態(tài)模型，如圖7所示，其中括號(hào)內(nèi)第一個(gè)權(quán)值為長(zhǎng)度，第二個(gè)權(quán)值為流量，第三個(gè)權(quán)值為時(shí)間。由圖7可知，規(guī)劃后的網(wǎng)絡(luò)由7個(gè)裝載站點(diǎn)、4個(gè)卸載站點(diǎn)、18個(gè)中間站點(diǎn)、45條實(shí)際路段組成。相對(duì)于規(guī)劃前的靜態(tài)網(wǎng)絡(luò)減少了1個(gè)站點(diǎn)和16條路段。使用本文方法對(duì)其進(jìn)行流量規(guī)劃后可知:系統(tǒng)在該時(shí)段內(nèi)可以承載的最大行李總數(shù)為2 485件，目前的系統(tǒng)配置是可以滿足該時(shí)段流量的需求的。

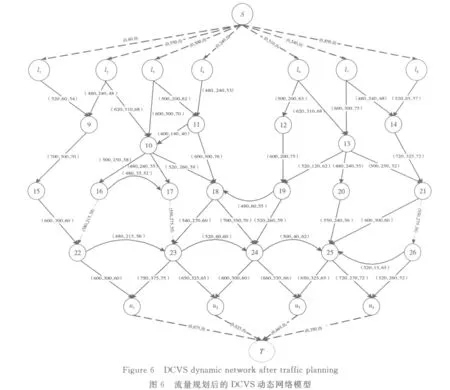
由本文所提出的動(dòng)態(tài)網(wǎng)絡(luò)流量規(guī)劃方法原理可知，即使在模型結(jié)構(gòu)規(guī)模擴(kuò)大、節(jié)點(diǎn)數(shù)增加的情況下，按照?qǐng)D4中的算法步驟，仍然可以實(shí)現(xiàn)對(duì)DCVS動(dòng)態(tài)模型的分析、規(guī)劃，從而得出對(duì)應(yīng)的最優(yōu)動(dòng)態(tài)流量規(guī)劃方案，確保系統(tǒng)內(nèi)的DCV小車運(yùn)輸時(shí)間最短的情況下得到整個(gè)運(yùn)輸網(wǎng)絡(luò)中的最大流量。

按照上述步驟分別使用本文方法對(duì)控制時(shí)段1、控制時(shí)段2和控制時(shí)段3的行李運(yùn)輸場(chǎng)景進(jìn)行了流量規(guī)劃仿真，結(jié)果如圖8所示。根據(jù)表1的實(shí)驗(yàn)結(jié)果可知:控制時(shí)段3和控制時(shí)段4一樣，當(dāng)前可以達(dá)到的最大流量滿足控制系統(tǒng)要求，但控制時(shí)段1和控制時(shí)段2中需要處理的行李量則超出了系統(tǒng)當(dāng)時(shí)配置所能達(dá)到的最大量，此時(shí)可以通過增開裝載站或卸載站的控制策略來滿足實(shí)際行李流的需求。表2列出了使用本文方法分析后需新增開的站點(diǎn)的數(shù)量變化情況及最大流量變化狀況。

Table 2 Flow after planning表2 規(guī)劃后的流量

由上述實(shí)驗(yàn)及結(jié)果可知:(1)本文方法可以實(shí)現(xiàn)基于最大流最短時(shí)間原理的動(dòng)態(tài)流量分析，為系統(tǒng)在不同時(shí)段的不同條件的流量規(guī)劃提供了基礎(chǔ);(2)在這個(gè)動(dòng)態(tài)規(guī)劃過程中，該方法可以準(zhǔn)確預(yù)測(cè)出當(dāng)前配置下DCV系統(tǒng)的整體最大可達(dá)流量，從而為系統(tǒng)的全局規(guī)劃提供了精確的依據(jù);(3)該方法在能夠保證流量最大化的同時(shí)優(yōu)化每個(gè)路段上的DCV車輛分配，因此可以縮短DCVS的整體運(yùn)行時(shí)間，提高DCVS和BHS的工作效率;(4)本文算法的運(yùn)算速度快，不會(huì)帶來額外的時(shí)間成本。

該方法綜合考慮DCVS流量和時(shí)間兩個(gè)重要因素的要求，可以根據(jù)DCVS不同時(shí)段內(nèi)的實(shí)際流量需求狀態(tài)來實(shí)現(xiàn)動(dòng)態(tài)分析和規(guī)劃，從而可以更好地利用資源，并為DCVS的控制提供實(shí)時(shí)的幫助。同時(shí)也為保障和提高整個(gè)控制系統(tǒng)的可控性和穩(wěn)定性提供了有效的解決方案。相對(duì)于目前DCV系統(tǒng)運(yùn)行過程中靜態(tài)無變化的固定路徑規(guī)劃方法，本文方法提供了一種更靈活更高效的全局系統(tǒng)流量規(guī)劃方法。

4 結(jié)束語(yǔ)

在實(shí)際的機(jī)場(chǎng)行李處理系統(tǒng)中，用于機(jī)場(chǎng)行李遠(yuǎn)端運(yùn)輸?shù)腄CV控制系統(tǒng)在每個(gè)不同的采樣時(shí)間區(qū)間內(nèi)的需求都是實(shí)時(shí)變化的，但實(shí)際的系統(tǒng)仍然采用傳統(tǒng)固定的規(guī)劃和控制方法，無法靈活地作出規(guī)劃，經(jīng)常造成控制資源的浪費(fèi)，影響了系統(tǒng)的行李處理效率。因此，有效地獲取系統(tǒng)的實(shí)時(shí)需求變化，并據(jù)此動(dòng)態(tài)地規(guī)劃DCVS的流量分配方案具有重要意義，也是迫切需要解決的問題。

本文圍繞上述問題對(duì)DCVS的動(dòng)態(tài)流量分析和規(guī)劃問題展開了研究，給出了一種基于動(dòng)態(tài)DCVS網(wǎng)絡(luò)模型的最大流最小時(shí)間的流量規(guī)劃方法。該方法實(shí)現(xiàn)了:(1)基于圖論的DCVS靜態(tài)網(wǎng)絡(luò)模型構(gòu)建;(2)遠(yuǎn)端行李處理系統(tǒng)在特定時(shí)間區(qū)間內(nèi)的綜合流量需求分析;(3)帶超級(jí)節(jié)點(diǎn)和超級(jí)匯點(diǎn)的DCVS靜態(tài)網(wǎng)絡(luò)模型的最大流最小時(shí)間算法實(shí)現(xiàn);(4)DCVS的整體流量分析和路徑流量分配;(5)基于Lingo平臺(tái)的實(shí)例仿真及結(jié)果分析。實(shí)驗(yàn)結(jié)果顯示，該方法可以根據(jù)DCVS不同時(shí)段的需求和配置動(dòng)態(tài)地完成對(duì)DCVS流量的整體規(guī)劃，并可以根據(jù)流量分析的結(jié)果判斷當(dāng)前系統(tǒng)的配置能否滿足實(shí)際需求，實(shí)現(xiàn)了對(duì)遠(yuǎn)端行李運(yùn)輸任務(wù)的流量任務(wù)預(yù)測(cè)，從而為DCVS的控制決策提供了重要依據(jù)。

附中文參考文獻(xiàn):