電子商務環境下賣家綜合評級的一種新方法

張定岳

摘要 為提高電子商務環境下賣家綜合評價水平，結合現實國情構建了網上賣家評級遞階模型，提出了一種基于層次分析法、三角模糊數等理論的賣家綜合評價新方法。該方法采用模糊AHP模型求取各層次指標權重，采用模糊關系矩陣確定各賣家的評語隸屬度，并結合隸屬度轉化模型層層歸并獲得評級結果。結果表明，該方法較好克服了人員評判的一定模糊性、群組決策難以歸并、待評賣家數量限制等問題，模型結構便于編程推廣，所得評級結果公平合理。

【關鍵詞】電子商務 賣家評級 層次分析法三角模糊數 隸屬度

經濟的快速發展和信息技術的不斷進步推動我國電子商務向縱深化、個性化和專業化發展。其中，電子商務環境下賣家綜合能力評價越來越受到平臺集成商、消費者和政策制定者的重視。賣家的綜合評價涉及商品、服務、物流、支付信用等諸多方面。對賣家進行科學、合理地綜合評級有利于促進賣家不斷自我完善，提高買家的信任和忠誠度，建立和諧的網上交易機制，推動電子商務的繁榮發展。

國內外目前已有不少關于電子商務環境下賣家綜合評級的理論研究和實踐應用成果，為現實問題的求解提供了很好思路。但總體而言，關于賣家遞階評價指標的確定以及評價算法的完善尚有改進空間。本文主要在文獻[1-3]的基礎上，基于現實國情進一步完善電子商務環境下賣家評級遞階模型，并在評價算法的設計過程中，充分考慮群組決策、評審人員評判的一定模糊性以及模糊判斷矩陣可能存在的不一致性等問題，基于層次分析法、三角模糊數等理論提出了電子商務環境下賣家綜合評級的一種新方法，以進一步提高對實際問題的處理能力。

1 相關模型和方法

1.1 模糊AHP模型

層次分析法（ Analytic Hierarchy Process，AHP）被廣泛應用于具有層級評價指標體系的決策問題中。在多方案群組決策問題中，AHP也可用于各層次指標權重的確定。其關鍵步驟是采用1-9間的整數比較值及其倒數作為標度構造判斷矩陣，但這種標度沒有考慮決策者對屬性或方案間比較評判的模糊性，在群組決策中也難以取得比較合理的共識。為此，引入三角模糊數來替代這種標度。

為確定遞階評價模型中某一層次中的指標權重wi，i=1，2，…n，n為該層指標數，一般要求n≦6（如果n﹥6，當要求一致性指標小于O.l，判斷矩陣一致性未通過率超過30%;而在現實評價中，無論是現場還是網絡打分，要求決策者或專家重新評價一般不具可行性）。在群組評價中，k=l，2，…，b，b為評判專家的數量。采用aijk表示專家k給出的指標i相對于指標j的重要性比較標度。令未歸一化前的同層次指標權重向量為W'=[W1'，…Wi'，Wn']T，采用對數最小二乘法可以得到Wt'滿足：

如果專家的評判標度采用三角模糊數，即aijk=（lijk，mijk，uijk），則可令wi'=（w'i，l，w'im，w'i，u），代入式（1）得到

結合三角模糊數的運算規則，由式（2）進一步求解得到：

將W歸一化為w=[w1，…，wi，-，Wn]T，其中wi=（wi，t，Wi，m，wi，u），得到

將式（3）.（5）代入式（6）進行求解，可以得到wi。

該模糊AHP模型充分考慮了評審人員對于指標重要性程度以及方案優劣性的比較評判的模糊性，并能有效綜合群組的評價意見。此外，該模型求解便利，易于編程和實現網絡化操作。

1.2 隸屬度轉化模型

在多方案評價過程中，對于某一方案在最底層指標集的評語等級隸屬度情況，往往采用模糊關系矩陣表示。設某最底層指標集（均隸屬于同一上級指標）為D={d1，d2，…，dn}，評語等級集為v={v1，v2，…，vm}（需要說明的是：評語等級一般按由好至差的次序排列，評語等級數m一般取[3，7]中的奇數），其相應分值集F={f1，f2，…，fm}，若該方案在指標u.上對vj評語等級的隸屬度為rij，則針對該方案評價的模糊關系矩陣R為：

例如，在物流服務評價中，D={d1，d2，d3}={配送準時性，產品完好度，服務滿意度），V={V1，v2，…，V5}={好，較好，一般，較差，差}。如果有20位專家在d1（配送準時性）指標上對該方案進行評價，4人認為“好”，9人認為“較好”，6人認為“一般”，1人認為“較差”，則

為實現方案隸屬度與指標權重的歸并，需要將模糊關系矩陣R中的每一行轉化為三角模糊數。令ri=R|di=[ri1 ri2 … rim]，轉化后得到Mi=（li，mi，ui）。令vt為max（ri1，ri2，… rim）對應的評語等級，t∈1，2，…，m，則vt的對應分值為ft，ft∈F。根據最大隸屬度原則，令該模糊三角數的mi值為ft，并令三角模糊數中的li、ui值分別為：

式中，數值項1/（i-t）或1/（t-j）主要是為了強調接近vt值的相應評語等級的作用。針對式（8），若評語等級的相應分值集F={f1，f2，…，f5）={1，0 5，0，-0.5，-1），則該隸屬度的三角模糊數表示為M1=（l1，m1，u1）=（0.325，0.5，0.6）.

需要說明的是，如果max{ri1，ri2，…，rim）對應的評語等級數量超過1個，則轉化得到的三角模糊數的mi=ft，，li、ui值根據式（9）、（10） 求解。例如ri=R|dt=[0.3，0.3，0.1，0.3，0]， 根據上述原則得到該隸屬度的三角模糊數為M=（li，mi，ui）= （0.3，0.5，0.65）。

該隸屬度轉化模型實現了各方案在不同指標下的模糊評價，從而使評價過程更符合人類判斷存在一定模糊性的現實情況，并能有效綜合評判者意見。同時，該模型能實現方案隸屬度與指標權重的歸并，由此層層歸并，最終得到評價結果。

1.3 總評值計算方法

若共有s個方案參與評級，設G為各方案在總評級目標下的評價結果向量，G=[g1，gk，…，gs]，k=1，2，…，s，其中gk=（lk，mk，uk）為三角模糊數，表示方案k的評價結果。為便于各方案的比較并得到確切的評級，有必要將方案的評價結果歸化為常數。根據經驗，群組的評價往往近似服從β分布的特點，可以采用式（11）來表示方案k的總評值，

顯然，tk值越大，則方案越優秀。需要說明的是：三角模糊數自身也有比值定義，但其數值之間的比較采用概率形式，直觀性略顯不足。

2 評價過程

2.1 確定評審人員、評價遞階模型、評語等級集及其相應分值集等

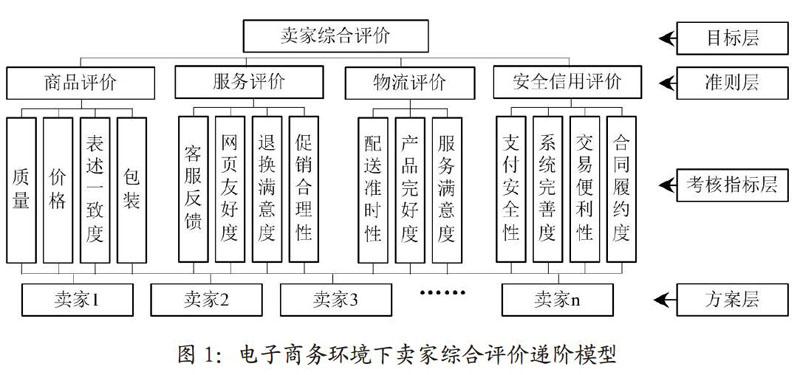
設評審人員數量為b，待評賣家數量為s。評價前，首先需要確定評價問題的遞階模型。與傳統的線下賣家比較，客戶對電子商務環境下賣家提出了更多的要求，例如物流服務、安全支付等。本文在參考文獻[1-3]的基礎上，并遵循同層次考核指標不能超過6個的原則（如前所述：如果同層次指標數量n≥7，模糊判斷矩陣一致性檢驗的未通過率將超過30%），提出電子商務環境下賣家綜合評價遞階模型，如圖1所示。其中一級指標層（即準則層）包括商品、服務、物流和安全信用共4個評價指標。每個準則下包括3-4個子指標（即考核指標），例如物流評價準則下包括配送準時性、產品完好度和服務滿意度等3個考核指標。以下評價步驟以該遞階模型為例。其次需要確定評語等級集和相應分值集。本文采用五級評語等級集V={v1，v2，…，v5}={好，較好，一般，較差，差}，相應分值集F={f1，f2，…，f5}={1，0.5，O，-0.5，-1）。

2.2 確定各準則以及各考核指標的相應權重

令{B1，…，Bk，…，Bs}為待評賣家集，{C1，…，Ci，…，Cn}為一級指標（即準則）集，由評審人員或評審小組對各準則進行重要性比較，給出相應的三角模糊數判斷矩陣，并計算得到準則權重向量W=[w1，…，wi，…，Wn]。令{Ci1，Ci，2，…，Ci，2）為隸屬于一級指標Ci下的二級指標（即考核指標）集（該集中的考核指標數量為1），同樣由評審人員給出模糊三角數判斷矩陣，求解得到其權重向量W，=[wi，1，wi，2，…，wi，1]。

2.3 計算各待評賣家在各準則下的評價結果

首先由評審成員確定各待評賣家在各考核指標下對于不同評語等級的隸屬度情況，由此得到各待評賣家在考核指標層下的模糊關系矩陣。然后采用隸屬度轉化模型將模糊關系矩陣中的行向量轉化為三角模糊數。令Ri=[Ri1，Ri2，…，Ris]為各待評賣家在準則ci下的三角模糊數關系矩陣，則可組合得到各賣家在總評價目標下的三角模糊數關系矩陣R=[RT1，…，RTi，…，RTn]T。

2.4 歸并得到各賣家在總目標下的評價結果

令Gi為各待評賣家在準則Ci下的評價結果向量：

Gi=Ri⊙Wi=[gi，1，…，gik，…，gi，s]（12）

設G為各待評賣家在總目標下的評價結果：

最后，采用式（11）計算得到各方案的總評值tk，k=1，2，…，s。結合目前我國電子商務環境下賣家現實運作狀況和人類模糊評價特點，本文設賣家綜合評級為優、良、中、合和差共五個評級，相應評值區間分別為[0.7，11、[0 5，0 7）、[0.3，0 5）、[O，0.3）和[-1，0）.

3 實例分析

我們在MATLAB環境下編程實現了基于上述算法和評價過程的電子商務環境下賣家綜合評級系統，涉及的主要實體和處理結果包括待評賣家、評審人員、評價指標、評價意見以及評審結果項等。本例中，有8家賣家參與評價，賣家綜合評價遞階模型如圖1所示。首先，由3組評審人員（包括3位學者、4位買家和3位賣家）提出針對4個準則的模糊判斷矩陣如式（14）所示。計算得到各準則的相應權重如表1所示。

關于3組專家給出的各考核指標在其隸屬準則下的模糊判斷矩陣，由于篇幅關系，本文不一一列出;基于這些判斷矩陣可得到各考核指標（二級指標）權重，如表2所示。

本文中賣家的評語等級集V={好，較好，一般，較差，差}，相應分值集F={1，0.5，0，-0.5，-1}，由10位評審成員確定待評賣家在各考核指標下對于各評語等級的隸屬度情況，從而得到各賣家在考核指標層下的模糊關系矩陣。因篇幅所限，本文中僅示例列出待評賣家Bl-B4在準則C1（商品評價）下的模糊關系矩陣式（15） - （18）。

式中Mk，的下標i表示考核指標，i=1，2，3，4，上標k表示待評賣家，k=1，2，…，8。

根據隸屬度轉化模型，進一步將式（15） -（18）轉化為三角模糊數列向量如式（19）-（22）所示。

組合R1、R2、R3，、R4，等得到8個待評賣家針對準則Cl的模糊關系矩陣R1=[R1，R2，…，R5]。同理可求得各待評賣家在準則C2、C3和C4下的模糊關系矩陣R2，R3和R4，從而組合得到各賣家在總評價目標下的三角模糊數關系矩陣R=[R1T，R2T，R3T，R4T]T。

表3列出了根據式（12）計算得到的各待評賣家在各準則（一級指標）下的評價結果。進一步根據式（13）和式（11）得到各賣家的三角模糊數評價結果、總評值以及相應評級，如表4所示。

由表4可以看出，待評賣家中B4最佳，B6其次，它們的總評值超過5，評級為良。其余6家賣家的總評值均在[0.3，0.5）之間，評級為中，它們之間的排序情況一目了然，其中B3最差。根據表3可以得到各賣家在不同準則下的評級以及比較情況，例如賣家B4的服務和安全信用評級很出色，但物流方面還有較大改進空間。此外，關于各賣家在不同考核指標下的評價情況也可以從相關三角模糊數關系矩陣中分析得到，受篇幅所限，本文不作進一步展開。

4 結論

目前國內外已有不少關于電子商務環境下賣家綜合評價的研究文獻，本文在此基礎上結合不斷發展的國內經濟和信息技術水平，進一步完善了電子商務環境下賣家綜合評級遞階模型。一些現有文獻中涉及的評價算法基于AHP展開，針對這些算法可能存在的模糊判斷矩陣不一致性、忽視人員評判的一定模糊性、未有效考慮群組決策、待評賣家數量限制等問題，本文提出了一種基于AHP、三角模糊數理論以及其它基本模糊理論的賣家綜合評價新方法。該方法采用基于三角模糊數的AHP求取各層次指標權重，采用模糊關系矩陣確定各待評賣家的評語等級隸屬度，并結合隸屬度轉化模型層層歸并獲得評級結果。實踐表明，該方法不僅較好解決或避免了上述問題，而且評價結果公平合理，所得建議豐富有益，易于編程實現和推廣應用。

參考文獻

[1]于兆吉，胡祥培，毛強，電子商務環境下信用評級的一種新方法[J].控制與決策，2009， 24 （11）：1668-1672.

[2]于兆吉，金仲，趙帥.基于賣方行為影響的電子商務在線信譽評價[J].東北大學學報（自然科學版），2013，34 （01）：149-152.

[3] Vavilis S，Petkovic M，Zannone N.A reference model for reputationsystems [J].Decision Support Systems，2014， 61（05）：147-154.

[4]劉新憲.選擇與判斷[M].上海：上海科學普及出版社，1990.

[5]韓伯棠.管理運籌學[M].北京：高等教育出版社，2010.