基于日n和Sc算法的大功率模塊散熱分析與優化

夏冬梅 楊俊逸 張志航 陳恒 劉祖耀 冉紅鋒 張儉

摘要

本文基于CFD理論基礎建立了某大功率模塊熱仿真模型，對模型進行了網格劃分與求解，對仿真結果進行了分析，指出了初始方案的不足之處通過Bn（熱瓶頸）和Sc（熱捷徑）等算法對該模塊散熱進行了優化，優化后的芯片最大溫差降低15℃，芯片最大溫度降低9℃，說明了Bn和Sc算法的有效性。本文所用到的散熱分析思路及優化算法亦對類似產品的散熱分析及優化提供了一定的參考意義。

【關鍵詞】散熱 熱仿真 熱瓶頸 熱捷徑

芯片的散熱方案設計合理與否直接影響產品的可靠性。10℃法則指出：電子元件工作溫度每升高10℃，失效率增大一倍以上。因此在大功率多芯片模塊的設計中，如何有效降低芯片溫度對提高產品的運行穩定性具有重要的意義。另一方面芯片溫度的不均勻也將直接導致PCB溫度的不均勻，可能造成PCB翹曲或機械應力等問題出現，因此芯片溫度的均勻化設計也顯得重要。

傳統的優化方案的提出，主要依靠熱設計工程師的經驗，首先提出可能的優化方向，然后再通過仿真驗證，這種方式費時費力且不一定能夠獲得較好的結果。鑒于此，國內外學者研究了模擬退火算法、遺傳算法，粒子群集法及嫡生成最小化法等先進優化算法，獲得了較好的優化結果，但是這些算法對使用者要求較高，需要較高的編程技巧。Bn（熱瓶頸）和Sc（熱捷徑）算法由Bryon Blackmore[6]等人于2010年提出，由于該算法無需編程，只需對仿真結果進行處理便能快速定位設計方案的問題點及優化方向，目前在國外得到了較大應用。

基于此，本文首先建立了某大功率模塊熱仿真模型，對仿真結果進行了分析，指出了初始方案的不足之處。通過Bn（熱瓶頸）和Sc （熱捷徑）算法對該模塊的散熱進行了優化，優化后的芯片最大溫差降低15℃，芯片最大溫度降低9℃，說明了Bn和Sc算法的有效性。

1 某大功率模塊熱仿真模型

1.1 控制方程

流體流動與傳熱要受最基本的3個物理規律的支配，即質量守恒、動量守恒及能量守恒，可以用通用方程形式描述以上規律：

式中：Φ為通用變量，可以代表U，V，W，T等求解變量;Γ_Φ為廣義擴散系數;S_Φ為廣義原項。式（1）中各項依次為瞬態項、對流項、擴散項和源項。

某大功率模塊等電子設備的熱分析被視為穩態過程，根據式（1）得到該模塊對流換熱的通用方程式：

利用有限體積法對上述控制微分方程在控制容積內進行積分，并引入邊界條件，便可得到求解變量的數值解。

1.2 模型建立

熱仿真建模一般包括幾何建模、物理參數設置、網格劃分及求解等4大部分，其中幾何建模包括幾何模型、功耗及材料參數等;物理參數設置包括求解域、初始條件與邊界條件的設置等，本文某大功率模塊建模在Icepak專業熱仿真軟件中進行。

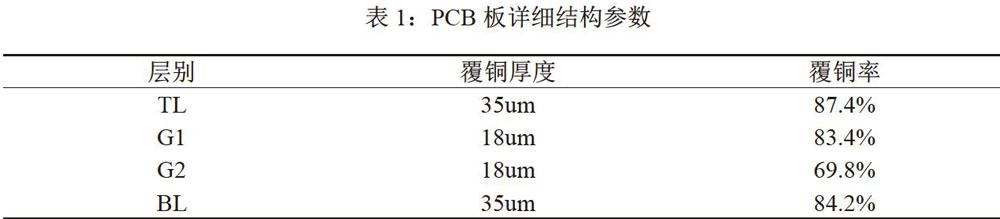
幾何建模主要包括模塊外殼、進出口風扇、PCB、芯片及散熱器的建模。其中外殼和散熱器的建模完全按照幾何實體建立，并賦予鋁擠6063材質;芯片的建模按照等尺寸block建立，并賦予10w的功耗及30W/mK的熱導率。進出風扇均為相同型號的軸流風扇，最大風量為200cfm，最大風壓為36mm H20，進出口風扇的建模采用軟件自帶的3D簡化模型按等尺寸建立，并根據風扇P-Q曲線輸入風量風壓值。PCB的幾何建模由63個表示有散熱通孔的PCB區域的Block模型和1個表示不帶散熱通孔的PCB區域的Block模型組成。PCB，散熱通孔結構參數見表1、2，將這些參數輸入Icepak軟件計算有散熱通孔和沒有散熱通孔的PCB區域的熱導率并賦值給以上Block，建立PCB幾何模型。

在Icepak軟件中設置與模塊等大的求解域，采用穩態湍流零方程模型，邊界條件為開放、溫度為環溫40℃，不考慮輻射影響。圖1所示為該模塊Icepak熱仿真模型。網格劃分采用HD網格并在戴爾服務器上進行劃分，單元數：4690347;節點數：4928828。

1.3 模擬結果與分析

對某大功率模塊熱模型進行求解計算，得到芯片溫度分布如圖2所示，由圖可知芯片溫度分布極不均勻，進風端芯片溫度低，出風端芯片溫度高，最大溫差近33℃，芯片最高溫度也達到90℃，散熱存在風險。

圖3所示為垂直PCB的某一截面的整體溫度分布，由圖可知，空氣從進口到出口溫度存在較大的溫度梯度，越接近進口風扇，空氣溫度越低，越靠近出口風扇，空氣溫度越高。這是由于每個芯片功耗相同且兩端都采用相同的散熱器，冷空氣從進口風扇吸進來以后，與第一個芯片的散熱器進行換熱被加熱后吹到第二個芯片的散熱器，又與第二個芯片散熱器進行換熱再次被加熱，以此類推，冷空氣被逐步加熱。

圖4所示為平行于中間板的某一截面速度分布，由圖可知，靠近出口風扇死區附近的芯片散熱器周圍空氣流速較低，熱空氣在此聚集不能及時排走，會進一步造成此處芯片溫度偏高，芯片溫差加劇，因此應避免在此處布置發熱芯片。

綜上所述，可知芯片存在較大溫差的主要原因是部分芯片處于出口風扇死區附近及芯片散熱器的均一化設計，下文將對這些不足之處進行優化

2 散熱優化分析

由前面分析可知，部分芯片處于出口風扇死區附近是造成芯片存在較大溫差的原因之一，可通過重新排布芯片即將PCB板上最靠近出口風扇的那列芯片移到其他地方來避開死區，本文重點研究Bn和Sc算法對PCB及散熱器的有效優化。

2.1 Bn和Sc優化原理

Bn和Sc由Bryon Blackmore和RobinBornoff于2010年提出，其思路是通過綜合熱通量矢量和溫度梯度矢量對傳熱效率進行判斷，并據此進行散熱設計優化。

如圖5所示，求解域中某一點的熱通量矢量和溫度梯度矢量的夾角為θ。

熱瓶頸定義為熱通量矢量和溫度梯度矢量的點積：

由式（1）得該點的Bn值為：

若分析域中某點具有較大的Bn值，由式 （4）可知：

（1）該點的熱通量大，即該點位于重要的熱傳遞路徑上;

（2）該點的溫度梯度大，即該點的熱阻大;

（3）|cosθ|=1，即熱通量矢量與溫度梯度矢量平行。

因此，Bn值大的區域說明熱量沿著熱阻大的路徑流動，通過優化設計減小這些區域的熱阻，能有效地降低溫升。

熱捷徑定義為熱通量矢量和溫度梯度矢量的叉積：

由式（3）得該點的Sc值為：

由式（6）可知，若分析域中某點具有較大的Se值，說明：

（1）該點的熱通量大，即該點位于重要的熱傳遞路徑上;

（2）該點的溫度梯度大，即該點的熱阻大;

（3）|sinθ|=1，即熱通量矢量垂直于溫度梯度矢量。

因此，Sc值大的區域說明熱量沒有沿著溫度梯度的方向流動，通過建立新的傳熱路徑，例如使熱通量與溫度梯度同向，能有效地提升固體傳熱效率。另一方面，文獻[9]也論述了Sc和努塞特數（Nu）的相關性，指出Sc與Nu有很強的相關性，即Sc值大的地方，Nu也較大，而Nu值是直接反映流體流動換熱強弱的物理量。換言之，Sc值大，流體流動換熱強;Sc值小，流體流動換熱弱。

基于以上說明，本文應用Bn和Sc算法的原則是改善Bn值較大的區域和Sc值較小的流體區域。

2.2 優化策略

本文大功率模塊模型十分復雜，如果對整機進行優化分析，則需要大量的計算時間。為節省計算時間，本文以中間板上的某一排的11顆芯片為分析對象建立簡化模型，并利用Bn和Sc算法對PCB及散熱器進行優化，再將散熱器優化結果復制到其它芯片和板上，最后對優化后的整機進行仿真并驗證優化效果。簡化模型：四個側面邊界條件為絕熱，前后邊界為固定流，空氣流量為風機最大風量的1/18。

2.3 優化分析與結果

對上述模型進行求解，并將結果文件導入CFD后處理軟件進行處理，得到初始方案的仿真結果，圖6所示為初始方案的芯片溫度仿真結果。由此圖可知，芯片最大溫差接近20℃，且越遠離進風口，芯片溫度越高。

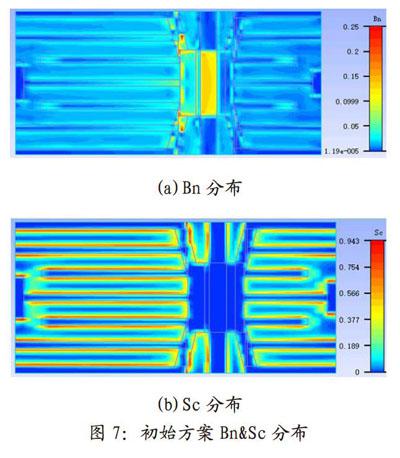
圖7（a）所示為初始方案Bn分布結果，由圖可知，Bn較大值分布在芯片對應的PCB區域和翅片較高的散熱器基座區域，說明這些區域存在較大的熱瓶頸，需要進行改善。

圖7（b）所示為初始方案Sc分布結果，散熱器翅片邊緣Sc值相對較大，翅片間隙中部Sc值相對較小。散熱器翅片邊緣Sc值大，說明與空氣的換熱相對較好，而翅片間隙中部Sc值小，說明此處與空氣的換熱不良，需進行改善。

由前面的Bn分析可知，初始方案的散熱瓶頸在于芯片對應的PCB區域和高的散熱器基座區域。由于芯片對應的PCB區域存在散熱通孔，可以通過增加散熱通孔個數或通孔鍍層厚度來改善。由于改善翅片較高的散熱器基座涉及到散熱器設計與重新開模，會帶來成本的增加，在這里我們不進行改善。

由前面的Sc分析可知，散熱器翅片間隙中部換熱不充分，可以考慮在此處增加翅片即加密散熱片來改善。但是并不是簡單地對芯片上的每個散熱器翅片進行加密，原因在于：一方面帶來散熱器成本的增加;另一方面翅片加密會帶來風阻的增加，可能造成后端風速降低較多，后端芯片散熱反而會惡化，同時也給風扇的選型帶來挑戰。因此在不更換風扇的前提下，需考慮在合適的芯片上加密散熱器，同時也要考慮散熱器安裝的便利性。

綜上所述，經過快速仿真及考慮到散熱器組裝的便利性，得到散熱器優化結果：保持遠離芯片的翅片高度較低的散熱器不變，將靠近進風口的3個翅片較高的散熱器更換成翅片較低的散熱器，將靠近出風口的3個翅片較高的散熱器翅片加密，中間5個翅片較高的散熱器保持不變。即靠近芯片的散熱器成前疏后密、前低后高的排列組合，以盡可能降低風阻。

圖8所示為散熱器優化后的芯片溫度的仿真結果，由此圖可知，芯片最大溫差接近10℃，比優化前降低了近10℃，同時最高芯片溫度也降低了4℃以上，說明了優化方案的有效性。

將上述散熱器優化結果復制到其它芯片，并將芯片對應區域的散熱孔由80增加到100個，重新建立整機模型進行仿真。由圖9可見，優化后芯片最大溫差由之前的約33℃降到約18℃，降低了15℃，同時最大芯片溫度亦由之前的約90，C降到約81℃，降低了約9℃，說明了Bn和Sc分析的有效性。

3 結論

（1）基于CFD理論建立了某大功率模塊熱仿真模型，指出芯片存在較大溫差的主要原因是部分芯片處于風扇死區附件及芯片散熱器的均一化設計，需進行散熱優化。

（2）利用Bn（熱瓶頸）和Sc（熱捷徑）算法對PCB及芯片散熱器進行了優化，芯片最大溫差由之前的約33℃降到約18℃，降低了約15℃，同時最大芯片溫度亦由之前的約90℃降到約81℃，降低了約9℃，說明了Bn和Sc方法進行散熱優化的有效性。

（3）本文所用到的散熱分析思路及優化算法亦對類似產品的散熱及優化提供了一定的參考意義。

參考文獻

[1]楊俊逸，謝家文，何彩英等.金融稅控收款機PCBA熱設計和熱分析[J]，電子機械工程，2010，26（03）：17-20.

[2]羅沛.基于模擬退火離散粒子群算法的芯片堆疊熱布局優化[J].現代計算機，2014（06）：16-20.

[3]Yuying Wang，Yunze Li，etal.“TheApplication of Genetic Algorithmfor Pin-fin Heat Sink OptimizationDesign”，2009 IEEE，ICIEA 2009，PP.2816-2821.

[4]MohdZainolarifinMohdHanafi，FatimahSham Ismail，etal.“Heat Sink Modeland Design Analysis Based on ParticleSwarm Optimization”，2014 IEEEInnovative Smart Grid Technologies-Asia（ISGT ASIA），pp.726-731.

[5]Jorge M.Cruz-Duarte，J.Gabriel Avina-Cervantes，etal.“Design of an optimalheat sink for microelectronicdevices using entropy generationminimization”，2015 IEEE，pp.231-235.

[6]John Parry，Robin Bornoff，ByronBlackmore，“Thermal BottleNecks andShortCut opportunities innovationsin electronics thermal designsimulation”Electronics CoolingMagazine，Vol.16，No.3，Fall 2010，pp.24-25.

[7]Robin Bornoff，Byron Blackmore，etal.“HeatSink Design Optimization Usingthe Thermal Bottleneck Concept”，2011 IEEE，27th SEMI-THERM Symposium，pp.76-80.

[8]Byron Blackmore，John Parry，etal.“Heat sink Design Optimization Usingthe Thermal ShortCut Concept”，2012IEEE，28thSEMI-THERM Symposium，pp.199-204.

[9]Robin Bornoff，John Wilson，etal.SUBTRACTIVE DESIGN：“A NOVEL APPROACHTO HEATS INK IMPROVEMENT”，2017 IEEE，33thSEMI-THERM Symposium.

[10]陶文銓.數值傳熱學（第2版）[M].西安：西安交通大學出版社，2001.