基于BP神經網絡預測正庚烷-乙醇混合燃料自燃溫度
陳若龍,韓永強,李潤釗,張一鳴,安東,孫博
(1.吉林大學汽車仿真與控制國家重點實驗室,吉林 長春 130022; 2.長春一汽四環發動機制造有限公司,吉林 長春 130013)
可燃物在沒有外部火源的作用下,因受熱或自身發熱所產生的自行燃燒稱為自燃,自燃溫度是在特定試驗條件下,可燃混合物在空氣中自燃的最低溫度[1-3]。近些年提出的反應控制壓燃(RCCI)雙燃料燃燒策略有提高內燃機燃燒熱效率、降低NOx及顆粒物排放的潛力[4-5],RCCI的雙燃料燃料特性需具有較大差異,因此本研究選擇正庚烷和乙醇作為燃料。正庚烷具有較高十六烷值,與柴油的自燃特性相似[6-7];乙醇辛烷值較高,抗爆性較好,因而作為汽油抗爆添加劑被廣泛應用。
人工神經網絡已經在智能控制、模式識別、組合優化和仿真預測等領域廣泛應用[8],其最具代表性的BP神經網絡特別適用于處理非線性問題。本研究中正庚烷-乙醇混合燃料的自燃溫度與其影響因素——正庚烷摻混比、當量比和進氣壓力之間是非線性關系,因而采用BP神經網絡來預測正庚烷-乙醇混合燃料的自燃極限。
1 試驗理論及方法
1.1 試驗條件
圖1示出定容燃燒彈試驗平臺原理。定容燃燒彈試驗平臺由進氣系統、定容燃燒彈彈體、燃油供給系統、噴油控制系統、溫控系統、排氣系統和數據采集系統組成。燃燒彈彈體材料采用45號鋼,設計安全壓力和溫度分別為28 MPa,900 ℃,其主要由上蓋板、燃燒室和下蓋板組成,采用螺栓進行連接,燃燒室為圓柱形,高為83 mm,直徑為132 mm,容積為1.014 L。進氣系統能夠精準控制進入彈體內的空氣壓力,當彈體內壓力達到預定壓力后,燃油供給系統將一定正庚摻混比的正庚烷-乙醇混合燃料注入燃燒室,以獲得具有不同當量比的可燃混合物。噴射壓力始終比燃燒彈彈體內壓力高出5 MPa,以促進均質可燃混合氣的形成。噴油脈寬和噴油次數由噴油控制系統來控制,在對燃燒室進行加熱之前要留有一定時間使燃料和空氣充分混合。電加熱管放置在燃燒彈彈體內部徑向106~116 mm處,用來對彈體進行加熱,通過調節調壓器改變加熱管對燃燒彈彈體的加熱功率,彈體外部的加熱圈起到輔助加熱和保溫的作用。通過溫度傳感器和壓力傳感器來檢測溫度和壓力的動態變化。3個溫度傳感器分別置于距離彈體底部42 mm,半徑為0,33,44 mm的3個徑向圓上。根據溫度標定試驗的結果分析,彈體內部最高溫度出現在徑向半徑為25~44 mm、軸向高度為35~55 mm的區域內,且該區域內溫度極限溫差在50 ℃以內,因此將溫度傳感器置于該區域內。排氣系統能夠及時把燃燒彈彈體內部的廢氣排出。高速同步采集系統將溫度和壓力信號傳送給LABVIEW系統。試驗設備見表1。

圖1 定容燃燒彈試驗平臺
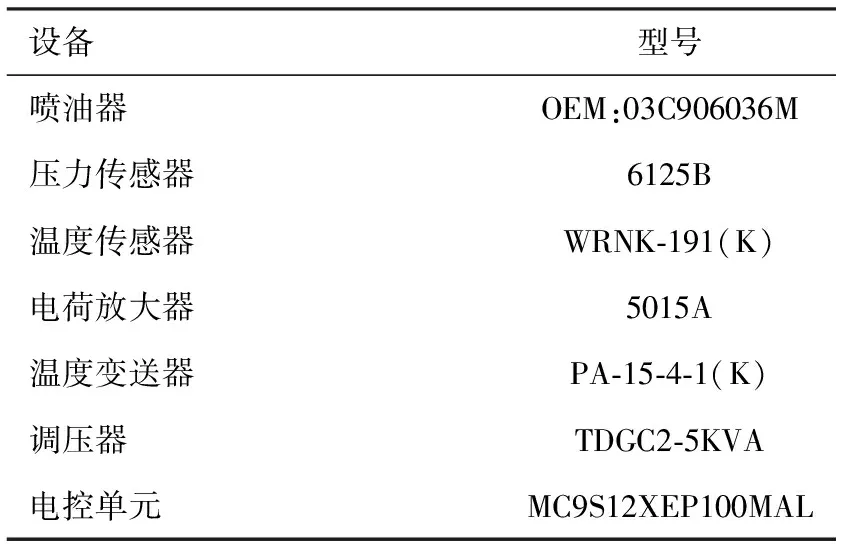
設備型號噴油器OEM:03C906036M壓力傳感器6125B溫度傳感器WRNK?191(K)電荷放大器5015A溫度變送器PA?15?4?1(K)調壓器TDGC2?5KVA電控單元MC9S12XEP100MAL
1.2 自燃判據
由于燃料在燃燒彈彈體內的燃燒是瞬間完成的,所以彈體內的溫度和壓力會在短時間內急劇增加。通過調節調壓器控制加熱管的加熱功率,從而使彈體內溫度在燃料起燃前緩慢增加。自開始對燃燒彈彈體加熱起,如果10 min內燃燒彈彈體內壓力比初始進氣壓力升高超過10%,同時溫度升高50 ℃以上,則判定均質可燃混合氣發生自燃,否則判定為沒有自燃[1-3,9-10]。
1.3 試驗步驟
不同正庚烷摻混比的正庚烷-乙醇混合燃料都要在定進氣壓力、變當量比或定當量比、變進氣壓力兩種模式下進行試驗。燃燒彈彈體容積為1.014 L(定容),當空氣的摩爾質量和進氣溫度保持不變時,由理想氣體的狀態方程可知進氣壓力保持不變。在試驗中進氣溫度設定為200 ℃。當進氣壓力保持不變時,可以通過改變燃料的摩爾濃度以獲得寬范圍的混合燃料當量比值。在化學計量條件下,空氣和燃料的摩爾濃度同時增加或同時減少,此時當量比保持不變。正庚烷-乙醇混合燃料的自燃溫度極限試驗中,正庚烷摻混比分別是1,0.75,0.5,0.25和0,當量比分別是0.4,0.6,0.8,1.0,1.2,1.4,1.6,1.8和2.0,進氣壓力分別為0.773,1.159,1.545,1.931,2.317,2.703,3.089,3.475,3.861 MPa,共405個試驗點。表2列出正庚烷摻混比為1,進氣壓力為1.931 MPa,變當量比條件下的試驗點。

表2 正庚烷在定進氣壓力下的試驗點
1.4 正庚烷-乙醇混合燃料自燃溫度
不同正庚烷摻混比的正庚烷-乙醇混合燃料自燃溫度隨進氣壓力和當量比變化的MAP圖見圖2至圖6。

圖2 正庚烷自燃溫度MAP圖

圖3 75%正庚烷25%乙醇混合燃料自燃溫度MAP圖
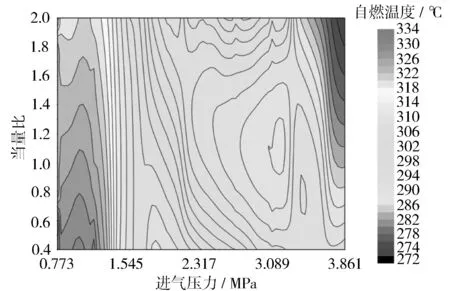
圖4 50%正庚烷50%乙醇混合燃料自燃溫度MAP圖

圖5 25%正庚烷75%乙醇混合燃料自燃溫度MAP圖

圖6 乙醇自燃溫度MAP圖
由圖2可知,正庚烷的最高自燃溫度出現在當量比為0.4~0.5,進氣壓力為0.773~1.159 MPa的較小區間內,隨著進氣壓力和當量比的不斷增加,正庚烷的自燃溫度逐漸減小。正庚烷的十六烷值較高,易燃,且在測試范圍內自燃溫差較小。
由圖3可知,對于正庚烷摻混比為75%的混合燃料,影響自燃溫度的主要因素是進氣壓力,隨著進氣壓力不斷增加,燃料自燃溫度減小。乙醇辛烷值較高,抗暴不易燃,因此添加25%乙醇后,混合燃料自燃溫度比正庚烷自燃溫度顯著提高。
由圖4可知,對于正庚烷摻混比為50%的混合燃料,在進氣壓力0.773~1.159 MPa區間的中間區域自燃溫度較高,最高自燃溫度出現在該壓力區間當量比較小的區域。隨著當量比的增加自燃溫度逐漸減小。定當量比時,隨著進氣壓力增加,自燃溫度逐漸減小。進氣壓力2.689~3.241 MPa,當量比0.8~1.4的區間內,自燃溫度相對較低,隨著當量比的增加或減小,自燃溫度都增加。
由圖5可知,對于正庚烷摻混比為25%的混合燃料,在進氣壓力較小且當量比較小時自燃溫度較高,進氣壓力介于1.159~1.207 MPa時,為自燃溫度的過渡階段,隨著進氣壓力和當量比的增加自燃溫度逐漸減小。隨著混合燃料中乙醇含量的增加,自燃溫度逐漸上升且自燃溫度極限溫差變大。
由圖6可知,影響乙醇自燃溫度的主要因素是當量比。乙醇最高自燃溫度出現在進氣壓力0.773~0.855 MPa,當量比0.4~0.5的較小區域內,自燃溫度隨當量比和進氣壓力的增加梯級減小且較為平穩。
結合圖2至圖6可知,隨著正庚烷-乙醇混合燃料中正庚烷摻混比的下降,燃料的自燃溫度和極限溫差均逐漸增加;當進氣壓力位于0.773~1.159 MPa區間時,自燃溫度明顯高于其他區間;當進氣壓力和當量比較小時自燃溫度較大,這說明當壓力低且均質燃料較稀時不易自燃,因此增加進氣壓力和當量比可以降低混合燃料的自燃溫度。
2 基于神經網絡的自燃極限模型
2.1 神經網絡模型的構建
搭建的神經網絡模型包括輸入層、隱含層和輸出層,影響正庚烷-乙醇混合燃料自燃溫度的主要因素正庚烷摻混比、當量比和進氣壓力作為輸入層參數,輸出層參數為燃料的自燃溫度。
正庚烷-乙醇混合燃料自燃溫度的405個試驗數據點中70%用于訓練神經網絡模型,以確保模型非線性的準確度,余下試驗數據分別用于對神經網絡的驗證和測試,以驗證神經網絡的泛化能力和預測精度。輸入層3個參數的量綱不同,會對隱含層各節點初始權值和閾值的選取造成一定的影響,為了消除不利影響和提高訓練神經網絡的收斂性,需要對輸入參數進行歸一化處理,將輸入參數處理為介于(0,1)之間的數值。歸一化公式如下:

(1)

由于輸入層參數歸一化后得到的輸出層數值也處于(0,1)之間,這與模型所需輸出值不相符,需要對其進行反歸一化處理。反歸一化公式為
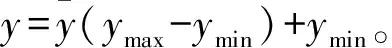
(2)
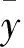
2.2 隱含層的選擇與誤差度量
研究表明,單層隱含層的神經網絡已經可以實現對真實輸出結果任意精度的逼近,因此本研究采用單層隱含層。隱含層節點的確定常采用經驗公式和試湊法相結合的方法。經驗公式為
(3)
式中:n為輸入層節點數;m為輸出層節點數;a為常數。
本研究采用Levenberg-Marquart計算預測誤差函數以訓練神經網絡模型,對算法中的權值、閾值和節點等相關信息進行初步設定。選用280個試驗點訓練模型,根據圖7迭代過程的均方誤差可知,第52次迭代時預測值和實際值的迭代誤差達到最小值,且其后的6次迭代的均方誤差均大于第52次迭代,迭代終止;由圖8可知,迭代到第52次時梯度最小,預測錯誤率最低,因此迭代第52次時對應的神經網絡模型即為本條件下的最優模型,此時隱含層層數為1,節點數為16。神經網絡模型結構見圖9。圖10、圖11分別示出神經網絡預測誤差直方圖和迭代結果回歸曲線。

圖7 迭代過程均方誤差

圖8 神經網絡訓練狀態

圖9 神經網絡模型結構

圖10 神經網絡預測誤差直方圖
由圖10可知,模型誤差基本在7 ℃以內,誤差相對較小,最大絕對誤差為12.63 ℃,相對誤差小于4.2%,但是試驗點較少,預測誤差總體上在允許的范圍內。由圖11可知,模型的訓練、驗證、測試和全局線性系數R分別為0.997 78,0.997 9,0.994 92和0.997 33,預測精度較高。

圖11 迭代結果回歸曲線
2.3 神經網絡模型泛化能力測試
為了驗證本神經網絡模型的泛化能力和預測精度,對本模型進行測試。進氣壓力為3.861 MPa時不同正庚烷摻混比例下燃料的自燃溫度見圖12。10%正庚烷和90%乙醇混合燃料的自燃溫度明顯低于乙醇的自燃溫度,稍高于25%正庚烷和75%乙醇混合燃料的自燃溫度。在乙醇燃料中添加正庚烷能夠明顯降低燃料的自燃溫度,即影響正庚烷-乙醇混合燃料自燃溫度的主要因素是正庚烷。90%正庚烷和10%乙醇混合燃料的自燃溫度與正庚烷自燃溫度較為貼合,因此在正庚烷燃料中添加10%乙醇對燃料的自燃溫度影響不大。綜合看來,隨著正庚烷摻混比的增加,燃料的自燃溫度隨之減小,符合正庚烷-乙醇混合燃料自燃溫度的變化趨勢。

圖12 神經網絡對正庚烷摻混比的泛化能力測試
圖13示出進氣壓力為1.931 MPa,不同當量比下混合燃料的自燃溫度。由圖可見,對于75%正庚烷和25%乙醇混合燃料,預測結果與試驗結果的絕對誤差均小于4.5 ℃,平均誤差為2.2 ℃,相對誤差小于0.79%;對于50%正庚烷和50%乙醇混合燃料,預測結果與試驗結果的絕對誤差小于3.2 ℃,平均誤差為2.4 ℃,相對誤差小于1.02%,均在允許的誤差范圍內。

圖13 神經網絡對當量比的泛化能力測試
圖14示出當量比為0.8時在不同進氣壓力下的自燃溫度。由圖可見,對于75%正庚烷和25%乙醇混合燃料,自燃溫度預測值與試驗值絕對誤差均小于5 ℃,平均誤差為2.84 ℃,相對誤差小于1.1%;對于50%正庚烷和50%乙醇混合燃料,自燃溫度的預測值與試驗值絕對誤差均小于3.5 ℃,平均誤差為2.3 ℃,相對誤差小于0.68%。結果表明本模型的預測值與試驗值具有良好的一致性,神經網絡模型具有較好的泛化能力。
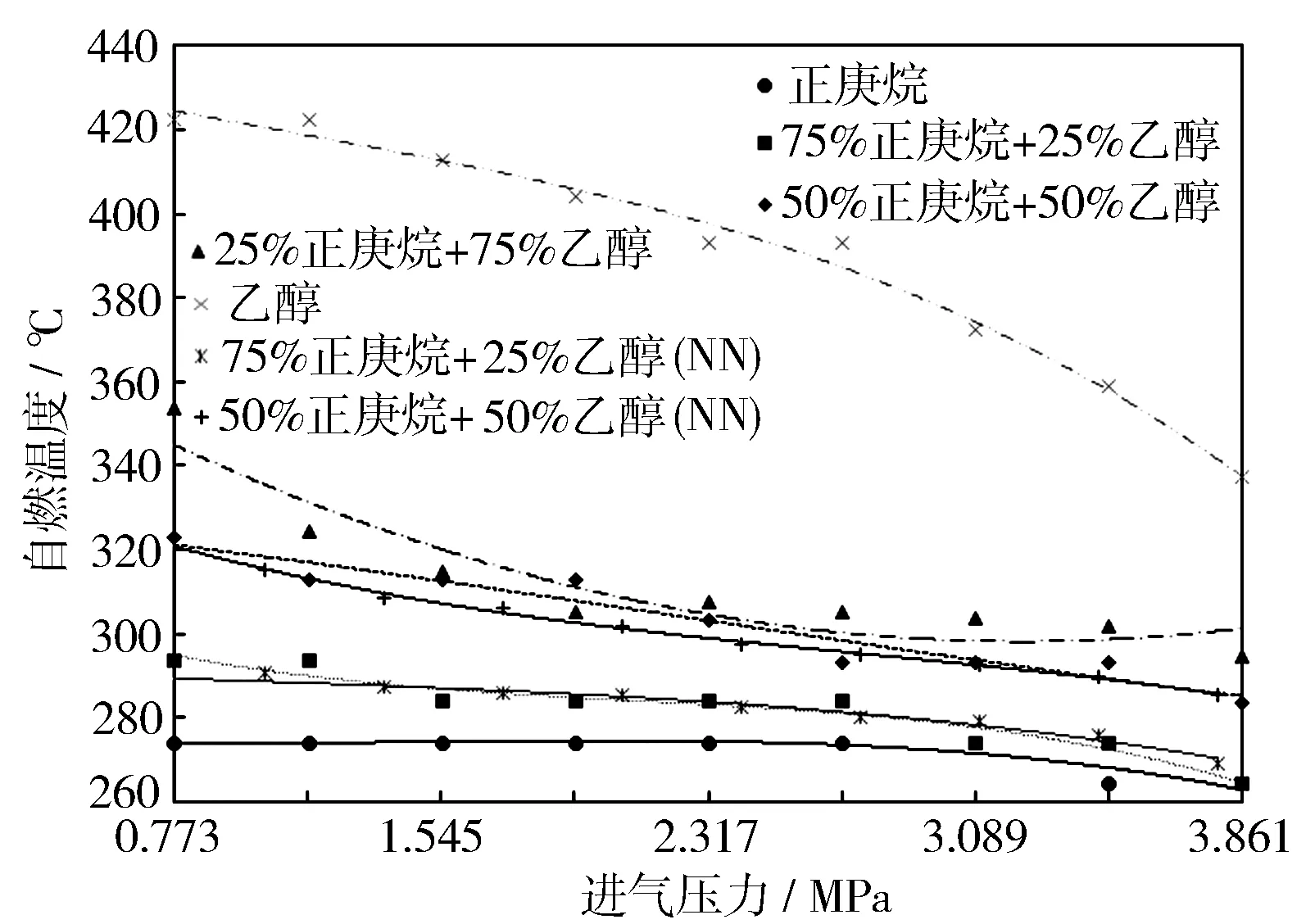
圖14 神經網絡對進氣壓力的泛化能力測試
3 結束語
利用定容燃燒彈試驗平臺得到了正庚烷-乙醇混合燃料自燃溫度分布。隨著正庚烷摻混比的下降混合燃料自燃溫度逐漸升高,自燃溫度極限溫差也逐漸增大,增加進氣壓力和當量比可以降低該混合燃料的自燃溫度,驗證了正庚烷易燃、乙醇不易燃的燃料特性。
利用正庚烷-乙醇混合燃料的405個試驗數據點搭建了以正庚烷摻混比、當量比和進氣壓力為輸入,自燃溫度為輸出的神經網絡模型;單層隱含層包含16個神經元時該神經網絡模型預測精度最高,訓練狀態最好;神經網絡模型預測誤差基本在7 ℃以內,誤差相對較小,最大絕對誤差為12.63 ℃,相對誤差小于4.2%,但是數據點較少,總體上在允許的誤差范圍內;對模型訓練、驗證、測試的線性系數和全局線性系數R分別為0.997 78,0.997 9,0.994 92和0.997 33,預測精度較高。
通過對神經網絡模型的測試,驗證了本模型對輸入層參數的泛化能力。在不同測試條件下,預測值與試驗值的絕對誤差、平均誤差和相對誤差均在允許范圍內,因此該神經網絡模型能夠很好地預測正庚烷-乙醇混合燃料的自燃溫度。
[1] European Standard EN 14522 Determination of mi-nimum ignition temperature of gases and vapors[S].[S.l.]:[s.n.],2005.
[2] ASTM Standard D 2883-95 Standard Test Method for ReactionThreshold Temperature of Liquid and Solid- Materials[S].West Conshohocken:ASTM,2009.
[3] Standard E 659-15 Standard Test Method for Auto-ignitionsTemperature of Chemicals[S].West Conshohocken:ASTM,2015.
[4] Reitz R D.Review of high efficiency and cleanreactivity controlled compression ignition (RCCI) combustion ininternal combustion engines[J].Energy Combust. Sci.,2015,46:12-71.
[5] Kokjohn S L,Hanson R M,Splitter D A.Fuelreactivity controlled compression ignition (RCCI):a pathway tocontrolled high-efficiency clean combustion[J].Int. J. Engine Res.,2011,12(3):209-226.
[6] Westbrook C K,Curran H J.Chemical kinetic modeling study of shock tube ignition ofheptane isomers[J].Int. J. Chem. Kinet.,2001,33(12):868-877.
[7] Mehl M,Pitz W J,Westbrook C K,et al. Kineticmodeling of gasoline surrogate components and mixtures underengine conditions[J].Proc. Combust. Inst.,2011,33(1):193-200.
[8] Hagan M T,Demuth H B.Neural network design[M].Boston:PWS Publishing Company,1996.
[9] Frurip D,Britton L,Fenlon W,et al.The role of ASTM E27 methods in hazardassessment: Part I. Thermal stability, compatibility, and energy releaseestimation methods[J].Process Saf. Prog.,2004,23(4):266-278.
[10] Britton L G,Cashdollar K L,Fenlon W,et al. The role of ASTM E27methods in hazard assessment. Part II:Flammability and ignitability[J].Process Saf. Prog.,2005,24(1):12-28.

