用GeoGebra軟件描繪電荷電勢分布

盛寶驥

(南京師范大學附屬中學,江蘇 南京 210003)

人教版高中物理選修3-1“靜電場”這一章節集中了較多的抽象概念,如電場強度、電勢.相比力學中的概念和模型,學生缺乏對電場的主觀體驗,學習過程中存在較多難點.

GeoGebra 是一個綜合幾何、代數與微積分的動態數學軟件,它是由美國佛羅里達州亞特蘭大學的數學教授Markus Hohenwarter所設計的.相比Mathematica、Matlab和Maple等專業軟件,GeoGebra不需要操作者熟悉復雜的計算機編程,更適合在中學教師和學生中推廣應用.下文介紹了筆者使用GeoGebra軟件描繪等量同種電荷和等量異種電荷電勢分布的過程.

1 等量同種電荷的電勢

打開GeoGebra軟件,在【視圖】中選擇【3D繪圖區】，軟件界面主要分為工具欄、代數區、繪圖區、3D繪圖區、輸入區一共5個區域(如圖1).

圖1 GeoGebra軟件界面

xOy平面上任意一點的電勢可以表示為

為了便于作圖,取kq=1代入,在輸入區輸入方程

如圖2所示,在3D繪圖區立刻呈現出該方程的三維圖像(如圖3所示).

圖2 輸入函數方程

圖3 等量同種電荷空間電勢分布

調節鼠標滾輪可以縮放圖像,移動鼠標的同時按住鼠標右鍵可以從不同視角觀察三維圖像,如圖4所示分別表示沿y軸和x軸方向觀察的結果.

(a) 沿y軸方向觀察

(b) 沿x軸方向觀察

圖5 兩個面相交

圖6 描繪兩個面的交線

以往教學過程常常研究等量同種電荷連線以及連線的中垂線上的電勢分布情況,這里也能實現.在輸入區輸入y=0,3D繪圖區立刻出現一個新的平面,即xOz平面,如圖5所示,在工具欄點擊【相交曲線】工具(如圖6),然后在3D繪圖區先后點擊兩個曲面,在代數區就會自動增加一個曲線方程(如圖7),該方程就是以上兩個面的交線方程.代數區每一個繪圖對象前面都有一個圓形圖標,該圖標的作用是在3D繪圖區顯示或隱藏繪圖對象,點擊兩個面的圓形圖標,隱藏著兩個面,只保留交線方程,然后沿y軸方向觀察,就可以得到等量同種電荷連線上電勢分布圖像(如圖8).

圖7 自動添加交線方程

圖8 等量同種電荷連線上的電勢分布

下面研究電荷連線的中垂線上的電勢分布,在輸入區輸入x=0(即yOz平面),用相同的方法畫出兩個面的交線,沿x方向觀察,可以得到等量同種電荷連線的中垂線上電勢分布(如圖9).這些圖與傳統教學過程的結論是一致的,并且更加科學嚴謹.

(a)

(b)

2 動態參數設定

在完成等量同種電荷的電勢分析之后,筆者嘗試將電荷設定為一個變量,可以根據需要設定其正負和大小,以便代表任意電性或電荷量的兩個電荷,便于師生探究.

在輸入區輸入“q1=1”,隨后q1=1就會在代數區出現,點擊q1=1前面的圓形圖標,在繪圖區就會出現一個可以拖動的滑動條,當拖動滑動條顯示“-1”時表示電荷量大小為1C的負電荷,右鍵點擊滑動條可以編輯滑動條的參數,在區間項目中可以修改滑動條的最大值、最小值和增量(如圖10).

(a)

(b)

圖11 等量異種電荷空間電勢分布

圖12 等量異種電荷連線上的電勢分布

3 高考題中的應用

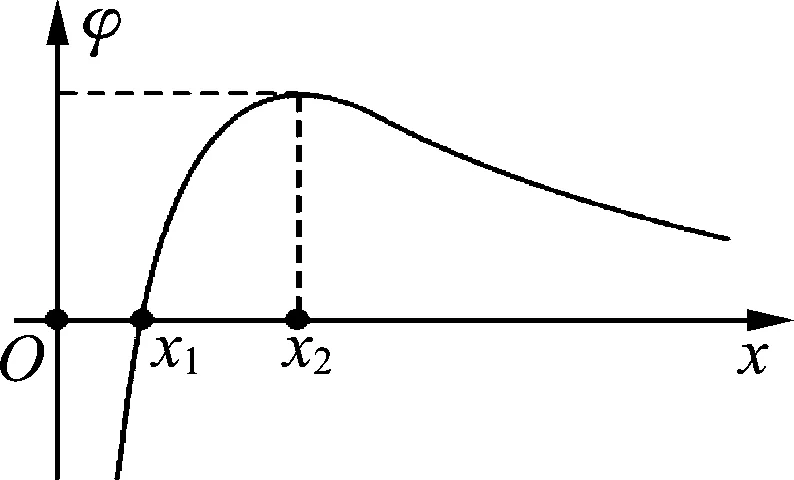
圖13

例1.(2017年江蘇省高考題)在x軸上有兩個點電荷q1、q2,其靜電場的電勢φ在x軸上分布如圖13所示.下列說法正確有

(A)q1和q2帶有異種電荷.

(B)x1處的電場強度為0.

(C) 負電荷從x1移到x2,電勢能減小.

(D) 負電荷從x1移到x2,受到的電場力增大.

題中的電勢φ在x軸上分布并不常見,什么樣的電荷才能形成這樣的圖像呢?從圖中可以發現,在x1的左側,電勢下降非常迅速,此處應該有一個負電荷,在x1的右側電勢先上升再逐漸下降,另外一個電荷為正電荷,且在x1的左側,由于x2的位置電勢為正,該位置距離負電荷更近,所以正電荷的電荷量一定大于負電荷的電荷量.根據這個判斷,筆者設定q1=-1,q2=10,還原了題目中電勢的三維分布圖(如圖14),通過畫著兩個電荷連線上的電勢分布,可以得到題目中圖像所對應的完整圖像(如圖15).

圖14 不等量異種電荷空間電勢分布

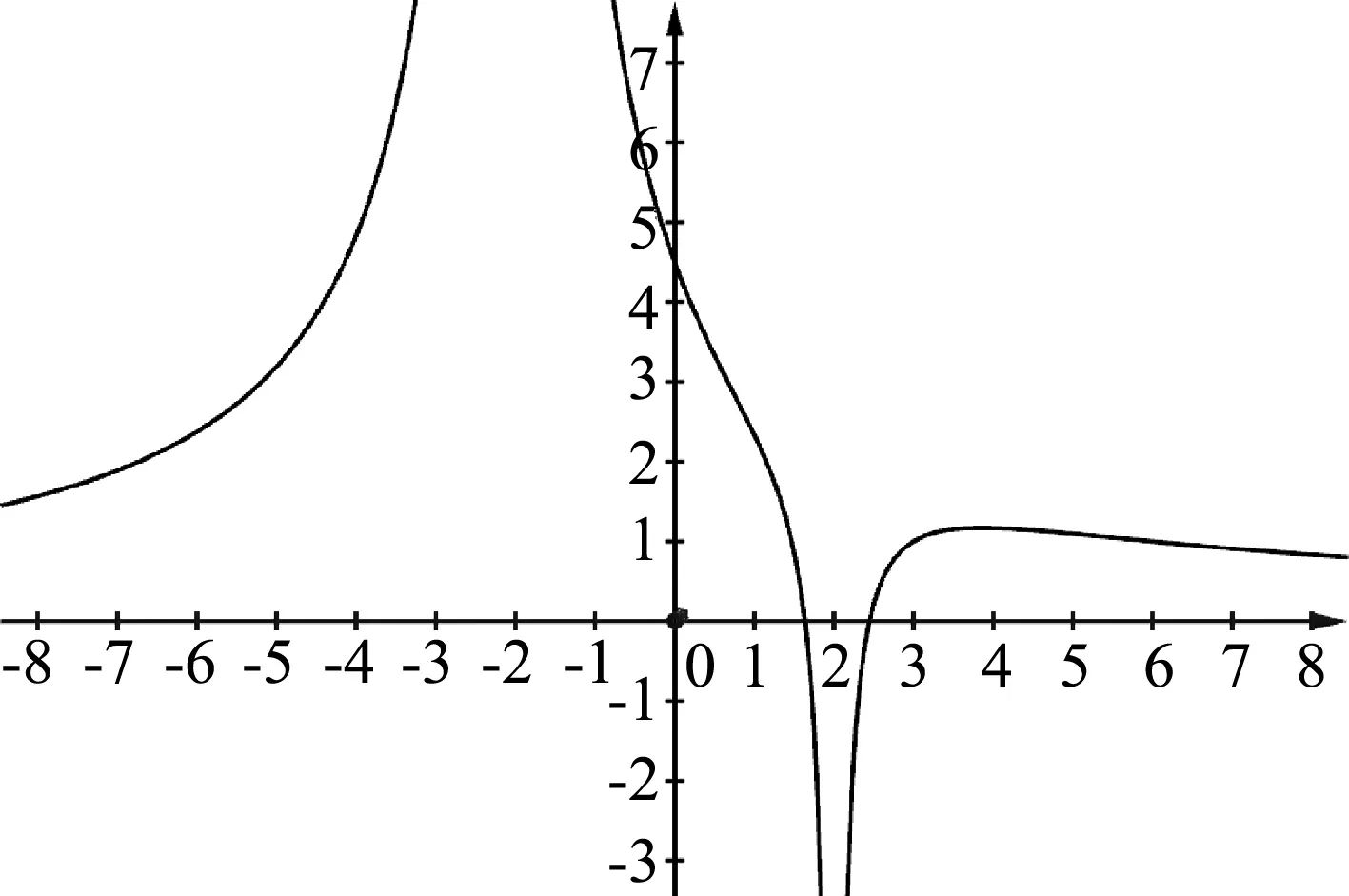
圖15 電勢φ在x軸上分布

4 總結與感悟

以往的教學中,只能粗略地畫出直線上的電勢分布,而且還要是等量電荷,現在通過GeoGebra軟件可以將一個平面上的電勢以三維立體圖的形式呈現出來,電荷量的大小也不再受限制,形象直觀可以旋轉的圖像給學生更好的視覺體驗,降低了學生學習抽象概念的難度,提升了教學效果.在教師的指導下,學生可以利用GeoGebra軟件開展豐富多彩的探究活動,結合GeoGebra軟件強大的繪圖功能,從不同視角體會物理之美.

1 人民教育出版社,課程教材研究所,物理課程教材開發中心.普通高中課程標準實驗教科書物理3-1[M].北京:人民教育出版社,2010: 18-19.

2 A Morphett, S Gunn, R Maillardet. Developing interactive applets with GeoGebra: processes, technologies[A]. Proceedings of Elephant Delta 15[C]. Port Elizabeth, 2015.