用材料力學方法研究不同模量梁的彎曲變形

吳曉，劉奇元，羅佑新

?

用材料力學方法研究不同模量梁的彎曲變形

吳曉，劉奇元，羅佑新

(湖南文理學院 機械工程學院，湖南 常德，415000)

為得到不同模量梁彎曲正應力及撓度的實用計算公式，采用材料力學方法分析復雜外載荷下的不同模量梁的彎曲變形，將材料力學方法得到的計算結果與彈性理論方法得到的計算結果進行比較。研究結果表明：用材料力學方法研究不同模量梁的彎曲變形不但計算精度較高，而且計算過程也簡便，克服了彈性理論存在一題一解及計算過程復雜繁瑣的缺陷；不同模量梁的剪切形狀因子與不同模量材料的拉壓彈性模量有關，而各向同性材料梁的剪切形狀因子與材料的彈性模量無關。

材料力學；模量；梁；彎曲變形；剪切；形狀因子

不同模量材料已經在工程中得到廣泛應用[1?7]。人們對不同模量材料對工程結構的影響也進行了相關研究，如：何曉婷等[8]得到了均布載荷下不同模量簡支梁的彈性解；王蔚佳等[9]在此基礎上進行了數值分析；吳曉等[10?12]則得到了線性分布荷載下不同模量懸臂梁的Kantorovich解、不同模量矩形截面桿和泡沫鋁芯夾層梁彎曲時解析解并進行了不同模量泡沫鋁芯夾層梁的彎曲計算分析；吳曉等[13]在考慮剪切效應的基礎上得到了不同模量梁的自由振動解析解[13]。若采用文獻[8?11]中的彈性力學方法，需要依靠三角級數進行求解，存在計算繁瑣、一題一解的缺陷，并且不能求解復雜外載荷作用下不同模量梁彎曲變形問題。文獻[12?13]采用各向同性材料梁的剪切形狀因子考慮剪切變形效應，但實際上不同模量梁的剪切形狀因子不再是常量，而與拉、壓彈性模量比值有關。基于以上原因，本文作者用材料力學方法研究不同模量梁的彎曲變形，得到其計算通式。

1 不同模量梁的應力計算公式

圖1所示為分布載荷作用下的等截面不同模量梁上的任意微段梁，有

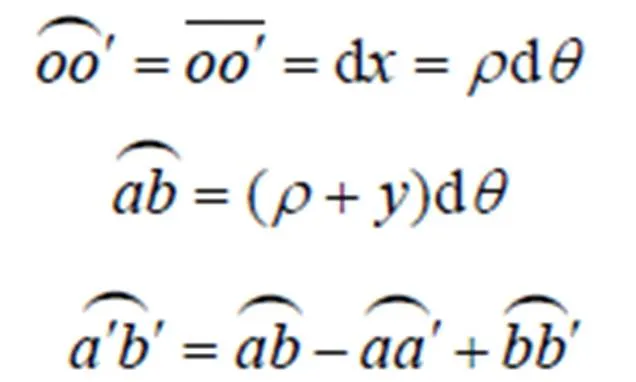
式中：為不同模量梁彎曲時的曲率半徑。

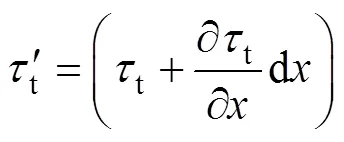
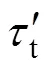
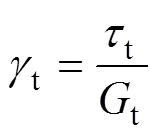
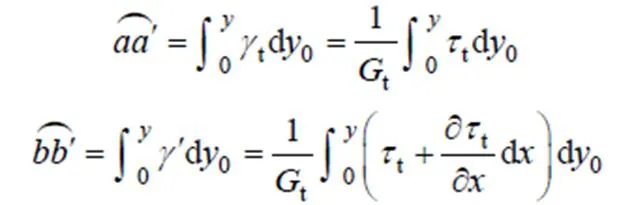
利用式(1)和(3)可得

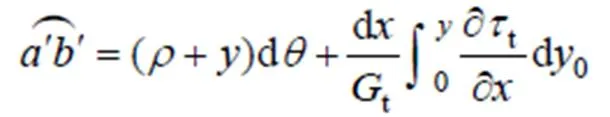
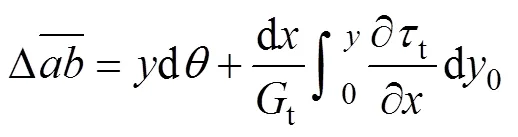
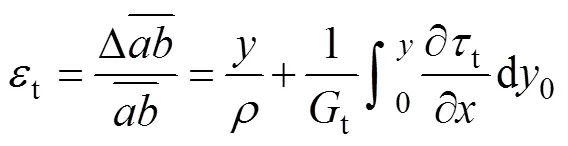
同理，可以得到不同模量梁壓縮區的線應變為

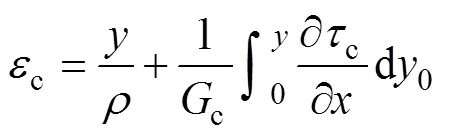
假設作用在圖2所示不同模量梁上的外載荷以向下為負，彎矩以使梁彎曲變形凸向下時為正。據文獻[13?15]可知不同模量梁純彎曲變形時拉伸區、壓縮區的彎曲應力分別為

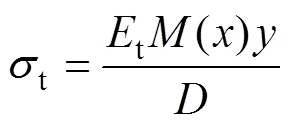
式中：為不同模量梁的抗彎剛度；t為拉伸彈性模量；()為梁截面彎矩。

圖2中，1和2分別為受拉區、壓縮區高度。

圖3(a)和圖3(b)所示分別為圖2所示簡支梁的受拉區、受壓區分離體。由圖3(a)可得1t和2t以及剪力方程為：

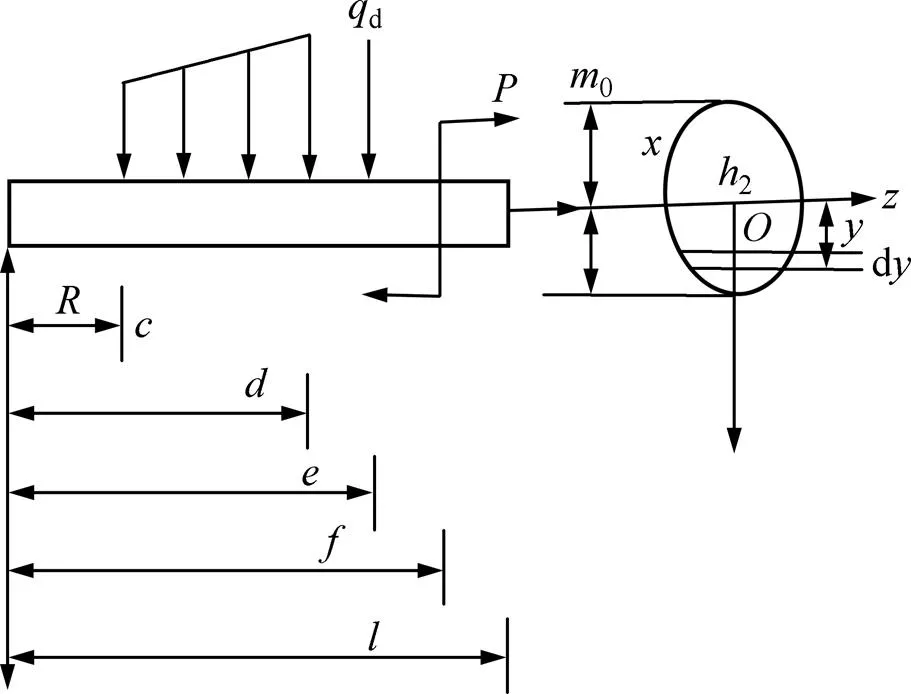
圖2 不同模量簡支梁

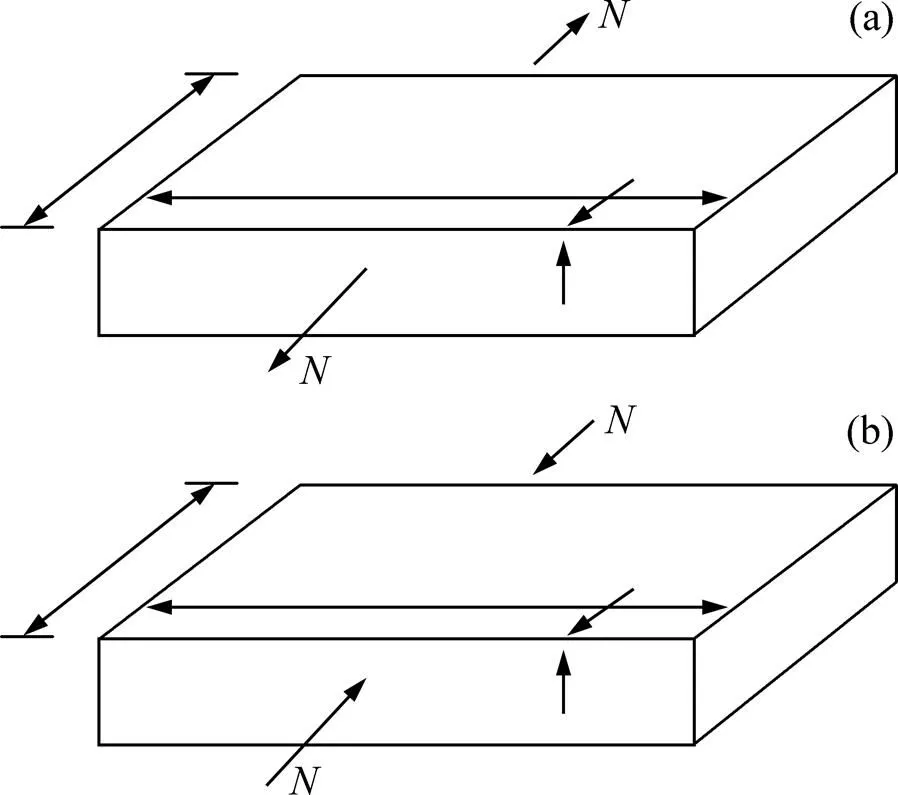
(a) 拉伸分離體；(b) 壓縮分離體

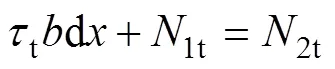
將式(7)中的拉應力公式代入式(8)可得

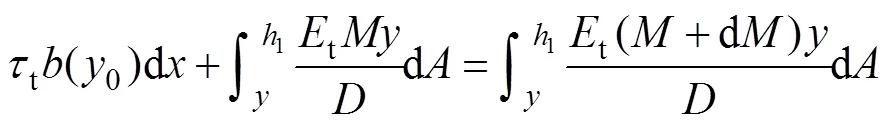
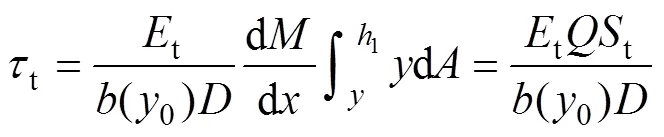
同理，由圖3(b)可得壓縮區彎曲剪應力c：

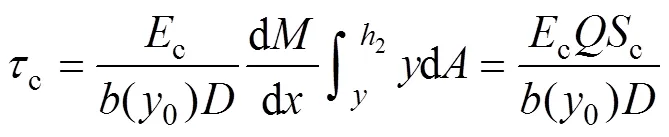
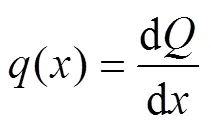
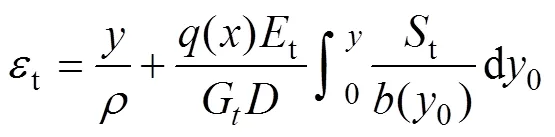
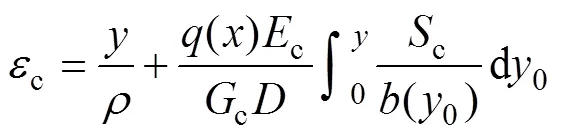
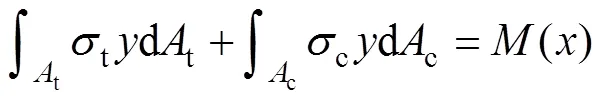
利用式(13)和(14)可得

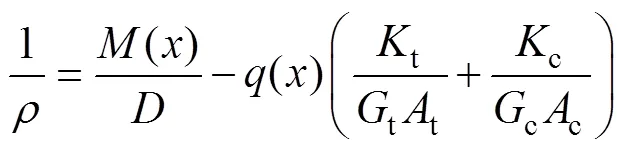
利用式(12)~(15)可知不同模量梁任意截面拉伸區、壓縮區的彎曲正應力分別為

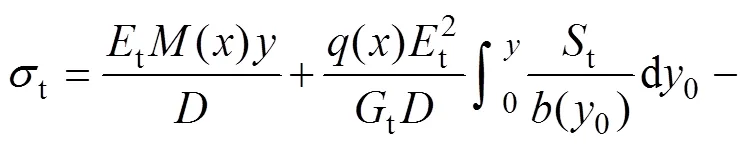
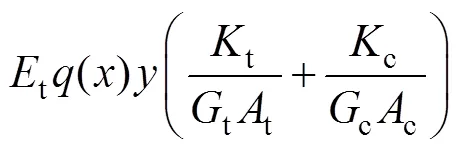
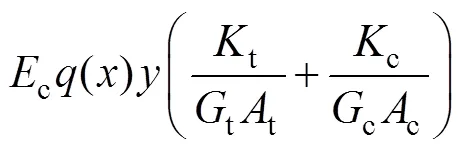
2 不同模量梁的撓度計算公式

為了使撓度計算公式具有普遍意義，以在復雜載荷作用下圖2所示不同模量梁為例，研究不同模量梁的彎曲撓度。

由式(15)可知不同模量梁的彎曲撓曲線微分方程為

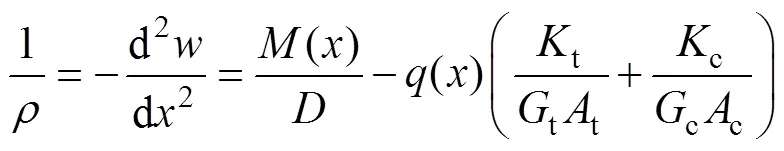
式中：為曲率半徑。

圖2所示不同模量梁在復雜載荷作用下的載荷集度可表示為

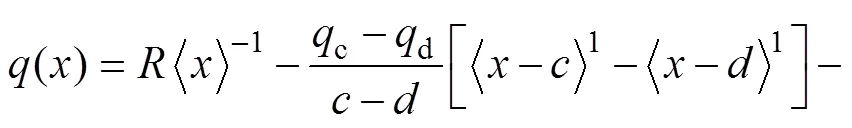
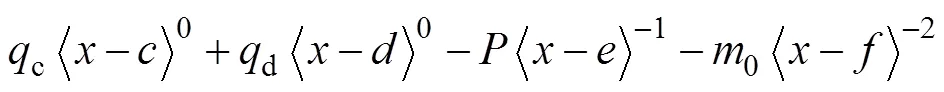
對式(19)進行1次積分可得剪力表達式為

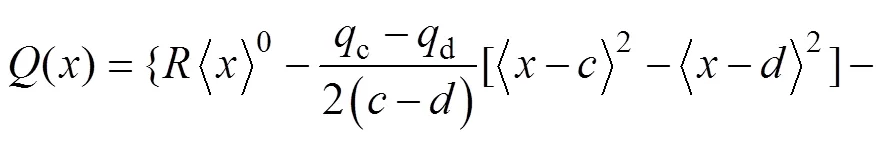
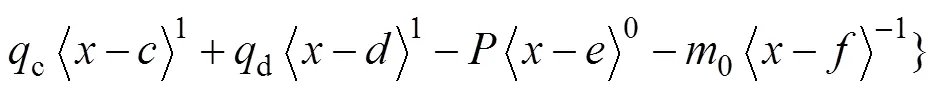
對式(20)進行1次積分可得彎矩表達式為

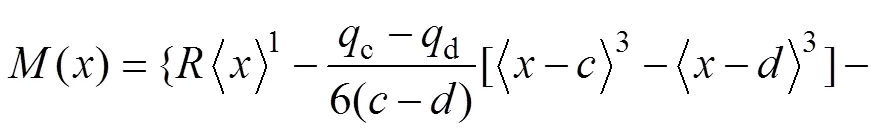
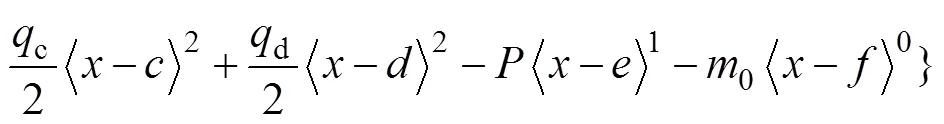
將式(19)和式(21)代入式(18)進行1次積分可得轉角方程為

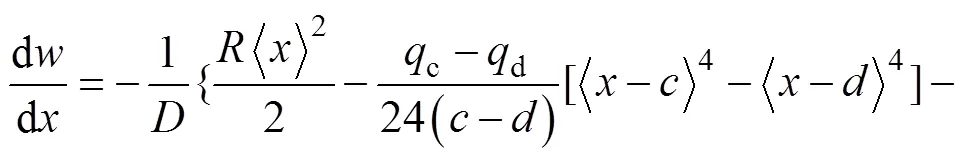
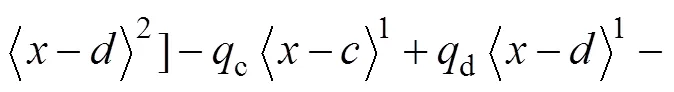
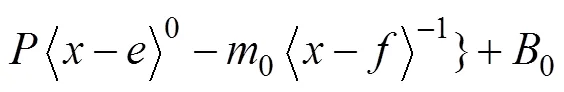
對式(22)進行1次積分可得撓曲線表達式為

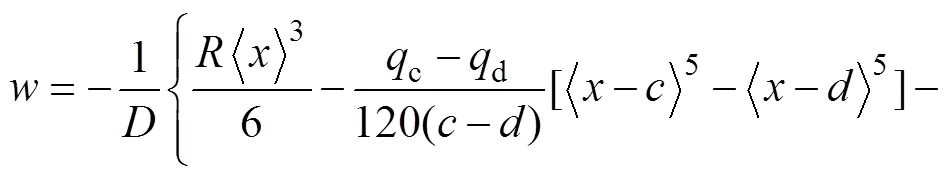
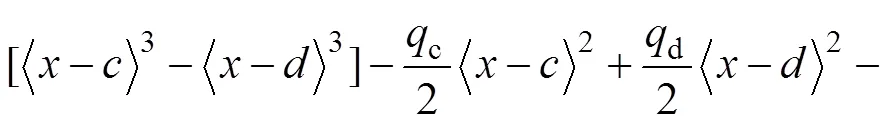
式中：0和1為待定積分常數，可根據不同模量梁的邊界條件來確定。

式(23)即為復雜荷載作用下的不同模量梁彎曲撓曲線表達通式。

3 計算分析及討論

算例1：均布荷載作用下簡支梁如圖4所示，該簡支梁由各向同性材料組成，均布荷載。

令t=c，可得

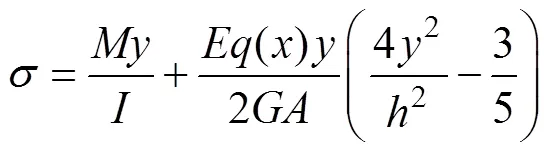
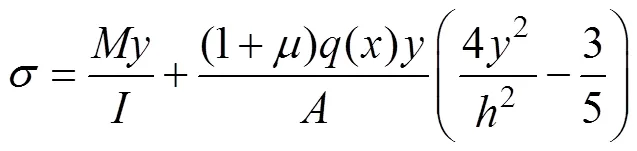
式中：為泊松比。在式(25)中，令=0，可得

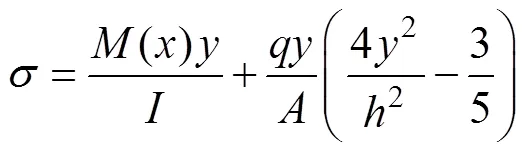
式(26)與彈性理論精確解相同[16]。

由式(23)可得

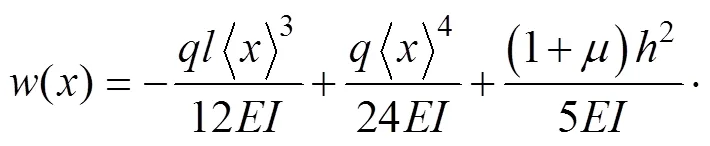
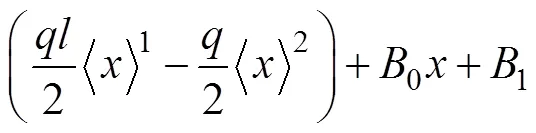
圖4所示簡支梁的邊界條件為

0，(0)=0；=，()=0 (28)

由式(27)和(28)可求得梁中點撓度為

式中：54/(384)為材料力學方法最大撓度解。

當=0.25時，由式(29)可得

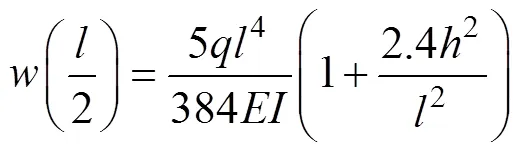
當=0.25時，由彈性理論可得梁的中點撓度為

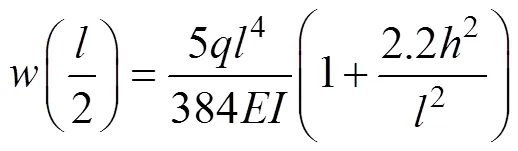
由式(25)可知當=0.25時，圖4所示簡支梁截面最大彎曲正應力為

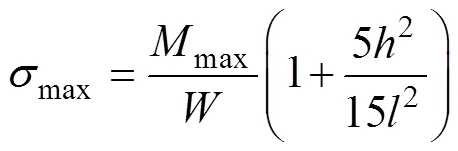
由式(26)可知圖4所示簡支梁截面最大彎曲正應力為

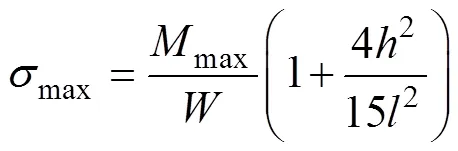
式中：max/為材料力學方法最大應力解；=2/6；max=2/8。

由式(30)~(33)所得計算結果見表1和表2。

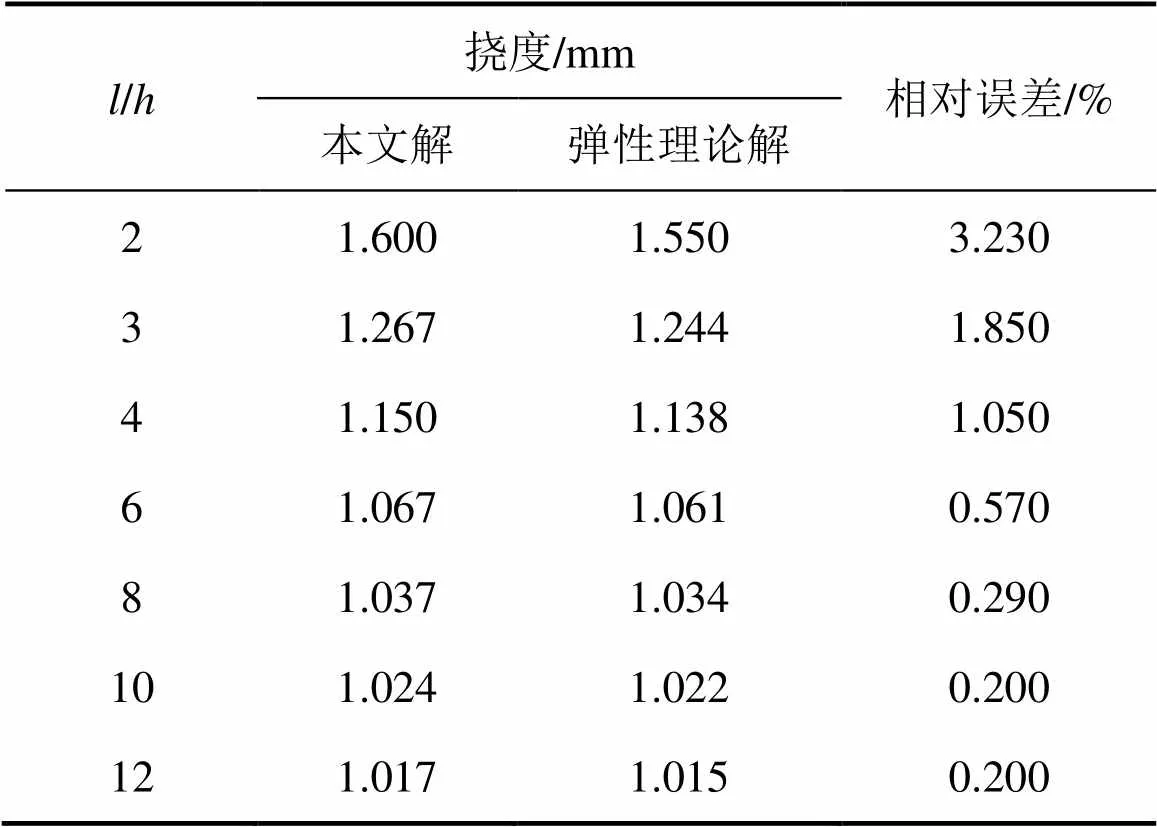
表1 梁中點撓度w(l/2)

表2 最大彎曲正應力

從表1和表2可以看出：采用材料力學方法計算結果與彈性理論解相差很小，計算精度高；即使當長高比/=2時，本文方法的撓度解和最大彎曲正應力解與彈性理論解的相對誤差分別為3.23%和1.50%，小于工程允許誤差5%；當/=6時，本文方法所得解和材料力學解與彈性理論解的誤差分別為0.57%和5.75%，因而，在計算/≤6的彎曲撓度時不宜采用材料力學方法，而應采用本文方法進行計算。

復雜外荷載下梁彎曲時的應力和位移彈性理論存在一題一解的缺陷，往往需要依靠三角級數，其計算量非常大。吳家龍[16]給出的式(26)和式(31)僅是均布載荷作用下梁應力、撓度解，采用本文方法則能給出復雜外荷載作用下梁的應力和撓度的計算通式，具有通用性和計算簡便的優點。

算例2：矩形截面懸臂梁由各向同性材料組成，均布荷載。其參數為：=3.0 m，0.5 m，=1.0 m，=10 kN/m，=210 GPa，80 GPa。其跨中彎曲應力彈性理論解為[16]

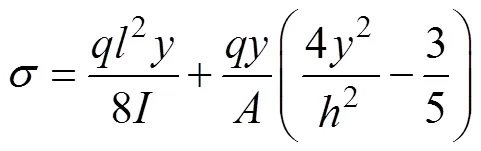
表3所示為懸臂梁跨中截面應力的本文方法、彈性理論方法和材料力學方法計算結果。

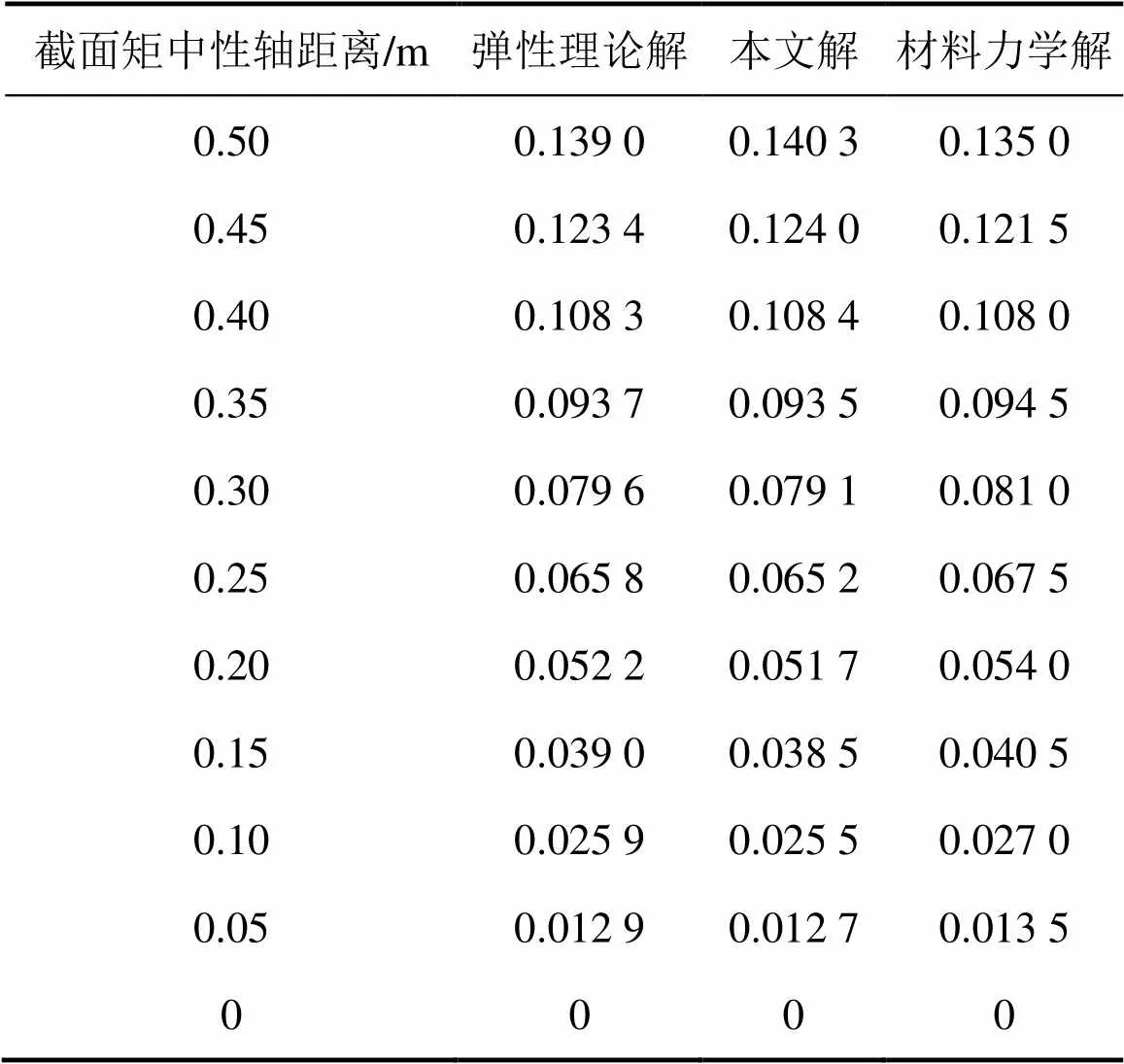
表3 懸臂梁跨中截面應力

從表1~3可知：當/≥3時，梁彎曲應力宜采用材料力學方法；當/＜3時，宜采用本文方法。因為本文方法計算精度較高，給出的是復雜外荷載下梁截面應力通解，而文獻[16]中方法僅限于求解均布荷載。

算例3：不同模量矩形截面梁材料參數及截面尺寸分別為：1=113 GPa，2=145 GPa，1=0.22，2= 0.292 6，=16 mm，=56 mm，132 kN/m。

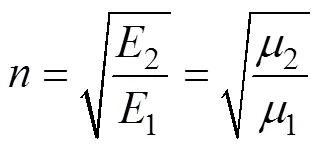
從表4~6可以看出：采用本文方法與采用彈性力學方法所得結果相差較小。對比表4和表5可以看出：將不同模量梁視為相同模量梁進行計算時，所得結果誤差較大。

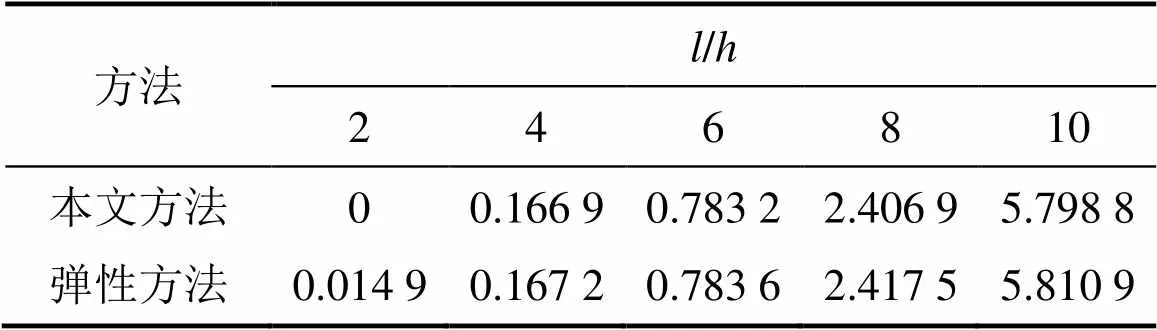
表4 E1=113 GPa，E2=145 GPa時不同模量簡支梁中點處撓度

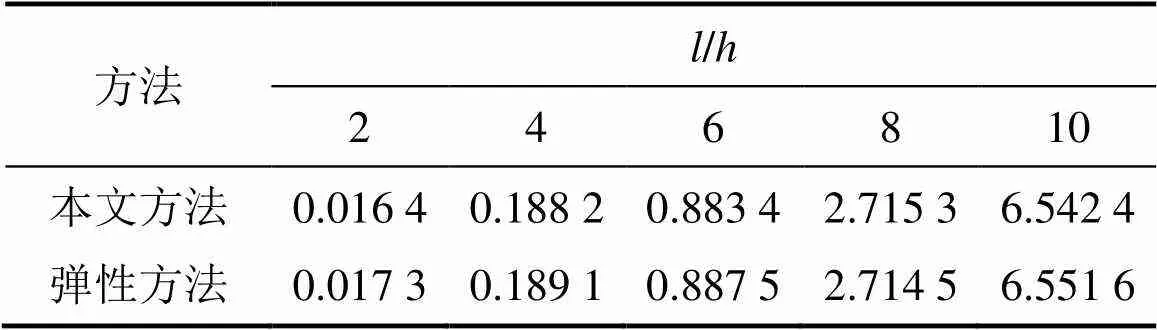
表5 E1=113 GPa，E2=145 GPa，μ1=0.22和μ2=0.292 6時各向同性簡支梁中點處撓度

表6 E1=113 GPa，μ1=0.22和l/h=10時不同模量簡支梁中點處撓度

4 結論

1) 本文所提出的方法克服了彈性理論存在一題一解的缺陷，得到了復雜外載荷作用下梁的彎曲正應力、剪應力和撓曲線通式，其計算簡便，計算結果具有很高的精度。

2) 進行彎曲變形計算時，將不同模量梁視為相同模量梁計算誤差較大，因而不同模量梁不能視為各向同性材料梁計算。

[1] 張國慶, 楊海天. 蟻群算法求解二維拉壓不同模量反問題[J]. 計算力學學報, 2014, 31(6): 687?692. ZHANG Guoqing, YANG Haitian. Ant colony algorithm based numerical solution for inverse bimodular problems[J]. Chinese Journal of Computational Mechanics, 2014, 31(6): 687?692.

[2] 楊海天, 張曉月, 何宜謙. 基于敏度分析的拉壓不同模量桁架問題的數值分析[J]. 計算力學學報, 2011, 28(2): 237?24. YANG Haitian, ZHANG Xiaoyue, HE Yiqian. Sensitivity analysis based numerical solution for truss structures with bi-modulus[J]. Chinese Journal of Computational Mechanics, 2011, 28(2): 237?242.

[3] 曹雪葉, 趙均海, 李艷, 等. 不同拉壓特性的厚壁球殼分析[J]. 應用力學學報, 2016, 33(3): 378?383. CAO Xueye, ZHAO Junhai, LI Yan, et al. Analysis on thick squash shell with different tension and compression properties[J]. Chinese Journal of Applied Mechanics, 2016, 33(3): 378?383.

[4] 杜玲, 李范春, 郭雪蓮, 等. 基于應力球張量法的不同模量陶瓷梁有限元分析[J]. 推進技術, 2015, 36(8): 1229?123. DU Ling, LI Fanchun, GUO Xuelian, et al. Finite element analysis of ceramic beam with different modulus based on stress balls tensor method[J]. Journal of Propulsion Technology, 2015, 36(8): 1229?123.

[5] MEDRI G. A nonlinear elastic model for isotropic materials with different behavior in tension and compression[J]. Transactions of the ASME, 1982, 26(104): 26?28.

[6] BERT C W, REDDY J N, CHAO W C, et al. Vibration of thick rectangular plates of bimodulus composite material[J]. Journal of Applied Mechanics, 1981, 48(2): 371?376.

[7] SRINIVASAN R S, RAMACHANDRA L S. Axisymmetric nonlinear dynamic response of bimodulus annular plates[J]. Journal of Vibration and Acoustics, 1990, 112(2): 202?205.

[8] 何曉婷, 陳山林, 孫俊貽. 不同模量簡支梁均布載荷下的彈性力學解[J]. 工程力學, 2007, 24(10): 51?56. HE Xiaoting, CHEN Shanlin, SUN Junyi. Elasticity solution of simple beams with different modulus under uniformly distributed load[J]. Engineering Mechanics, 2007, 24(10): 51?56.

[9] 王蔚佳, 鄒文成, 陳強. 基于雙模量理論的均布載荷下簡支梁的解析解及數值分析[J]. 工業建筑, 2013, 43(6): 56?59. WANG Weijia, ZOU Wencheng, CHEN Qiang. Analytical solution and numerical analysis for simply supported beams under uniform distributed loads based on bimodular theory[J]. Industrial Construction, 2013, 43(6): 56?59.

[10] 吳曉, 楊立軍, 黃翀, 等. 雙模量懸臂梁在線性分布荷載作用下的Kantorovich解[J]. 中南大學學報(自然科學版), 2014, 45(1): 306?311. WU Xiao, YANG Lijun, HUANG Chong, et al. Kantorovich solution for bimodulous cantilever under linear distributed loads[J]. Journal of Central South University(Science and Technology), 2014, 45(1): 306?311.

[11] 吳曉, 羅佑新. 拉壓彈性模量不同矩形截面桿的彎曲[J]. 西安建筑科技大學學報(自然科學版), 2013, 45(4): 493?498. WU Xiao, LUO Youxin. Bending of rectangular section bar with different elastic modulus in tension and compression areas[J]. Journal of Xi’an University of Architecture & Technology(Natural Science Edition), 2013, 45(4): 493?498.

[12] 吳曉, 楊立軍. 雙模量泡沫鋁芯夾層梁的彎曲計算分析[J]. 應用力學學報, 2015, 32(6): 63?67. WU Xiao, YANG Lijun. Bending calculation analysis of bimodulous aluminum foam sandwich beam[J]. Chinese Journal of Applied Mechanics, 2015, 32(6): 63?67.

[13] 吳曉, 黃志剛, 楊立軍. 考慮剪切效應時雙模量梁的自由振動[J]. 振動與沖擊, 2015, 34(24): 160?163. WU Xiao, HUANG Zhigang, YANG Lijun. Natural vibration of bimodulous beam considering shear effect[J]. Journal of Vibration and Shock, 2015, 34(24): 160?163.

[14] 鐵摩辛柯 S, 蓋爾 J. 材料力學[M]. 韓耀新, 譯. 北京: 科學出版社, 1990: 378?380.TIMOSHENKO S, GAL J. Mechanics of materials[M]. HAN Yaoxin, trans. Beijing: Science Press, 1990: 378?380.

[15] 阿巴爾楚米揚. 不同模量彈性理論[M]. 鄔瑞鋒, 張允真, 譯. 北京: 中國鐵道出版社, 1986: 13.AMBARTSUMYAN S A. Elasticity theory of different modulus[M]. WU Ruifeng, ZHANG Yunzhen, trans. Beijing: China Railway Press, 1986: 13.

[16] 吳家龍. 彈性力學[M]. 北京: 高等教育出版社, 2001: 117?129.WU Jialong. Elastic mechanics[M]. Beijing: Higher Education Press, 2001: 117?129.

Research of bending deformation of beam with different modulus by material mechanics method

WU Xiao, LIU Qiyuan, LUO Youxin

(College of Mechanical Engineering, Hunan University of Arts and Science, Changde 415000, China)

In order to get the practical calculation formulas of bending normal stress and deflection of the beam with different modulus, the material mechanics method was used to research the bending deformations of the beam with different modulus under external load. The calculation results obtained by the material mechanics method were compared with those obtained by the elastic theory. The results show that the accuracy is high and the procedure is simple for calculating the bending deformations of the beam with different modulus. This method overcomes the defects of elastic theory that one problem is with one solution and that the calculation process is complicated and cumbersome. The shear shape factor of the beam with different modulus is related to the elastic modulus of tension and compression of the different modulus material, and the shear shape factor of the beam with isotropic material is independent of the elastic modulus.

material mechanics; modulus; beam; bending deflection; shear; shape factor

10.11817/j.issn.1672?7207.2018.12.010

O341

A

1672?7207(2018)12?2972?07

2017?12?22；

2018?02?10

湖南省科技計劃項目(2011SK3145)；湖南“十二五”重點建設學科項目(湘教發［2011］76號)；湖南省自然科學基金資助項目(2015JJ6073)(Project(2011SK3145) supported by the Hunan Science and Technology Plan; Project((Hunan Education[ 2011]76)) supported by Hunan “Twelfth Five-Year Plan” Key Construction Subject; Project(2015JJ6073) supported by the Natural Science Foundation of Hunan Province)

吳曉，教授，從事工程力學研究；E-mail：wx2005220@163.com

(編輯 陳燦華)