深刻理解“新定義”，預設“鋪墊式”問題

仲世龍

[摘? 要] 當前新定義考題風行各地，如何開展新定義考題教學，以免出現“一帶而過”的低效教學是值得認真思考的課題. 首先，教師要深刻認識新定義考題的本質或結構特征，然后預設出一些鋪墊式問題，帶領和促進學生自主發現問題思路，讓學生既學會解題，又發展學生的解題自信.

[關鍵詞] 新定義考題;深刻理解;鋪墊式問題

新定義考題是近年來風行各地的一種熱點題型，由于有一定的閱讀量且需要深入理解，思考定義的本質或問題結構特征，所以這類習題在講評時不宜一帶而過，需要教者在課前基于新定義問題的深刻理解而預設一系列的鋪墊或一些“預熱式”教學環節，通過這些教學舉措拉長學生思考、理解的過程，達到較好的教學效果. 本文選擇一例新定義模考題，解析思路并給出教學微設計，跟進教學思考，提供研討.

考題及思路解析

1. 模考題

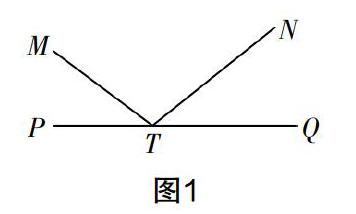
如圖1，直線PQ同側有兩點M，N，點T在直線PQ上，若∠MTP=∠NTQ，則稱點T為M，N在直線PQ上的投射點.

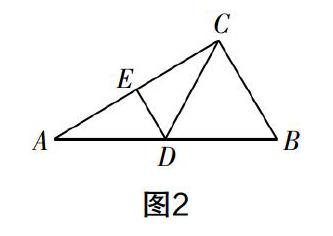
（1）如圖2，在Rt△ABC中，∠B=60°，D為斜邊AB的中點，E為AC邊中點. 求證：點D為C，E在直線AB上的投射點;

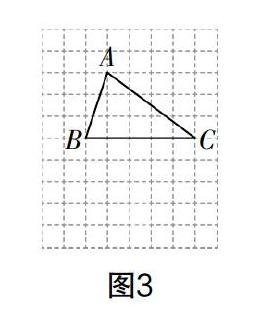
（2）如圖3，在正方形網格中，已知點A，B，C三點均在格點上，請僅用沒有刻度的直尺在AC上畫出點P，在BC上畫出點Q，使A，P在BC上的投射點Q滿足CQ=2BQ;

（3）如圖4，在Rt△ABC中，∠C=90°，AC=BC，在AB，BC邊上是否存在點D，E，使點D為E，C在AB上的投射點，點E為A，D在BC上的投射點？若存在，求出DE/CD的值;若不存在，請說明理由.

2. 思路解析

（1）理解新定義“投射點”后，想清證明的關鍵就是證出∠ADE=∠BDC，而所給的△ABC是一個含60°的特殊直角三角形，結合D為AB中點容易得出△BCD為等邊三角形，且有CD=AD，于是結合E為AC中點，可由“三線合一”證出DE⊥AC，從而得出△ADE也是含有30°，60°的特殊直角三角形，即∠ADE=∠BDC=60°.

（2）對于投射點的新定義，還可與光線反射模型或“將軍飲馬”模型關聯起來理解. 對于這一小問中要求的“CQ=2BQ”，可以借助于格點實現點Q的精準定位. 如圖5，取兩個格點M，N，用直尺連接MN交BC于Q點，根據相似三角形性質可得點Q是符合要求的“CQ=2BQ”.

接下來結合將軍飲馬模型逆運用確定點P的位置，可取點A關于直線BC的對稱點A′，作射線A′Q，交AC于點P，如圖6，所以點P即為所求.

（3）這一小問本質是將軍飲馬模型的又一變式，如圖7，分別取點A關于直線BC對稱點A′，取C關于直線AB對稱點C′，連接A′C′交AB，BC于點D，E，根據對稱性質，容易證出點D，E為所求的所謂“投射點”.

接下來求DE/CD的值，在圖7中，想清點A，C，B，C′恰是正方形的頂點，點E恰為BC中點，則有助于“看出”解答：DE/CD=BE/AC=1/2.

解題教學微設計

定義：如圖1，直線PQ同側有兩點M，N，點T在直線PQ上，若∠MTP=∠NTQ，則稱點T為M，N在直線PQ上的投射點.

1. 給出定義，初步理解

例1? 如圖8，在Rt△ABC中，∠B=60°，E為AC邊的中點.

（1）點D為邊AB的中點時，點D是否為C，E在直線AB上的投射點？簡要說明理由.

（2）在（1）的條件下，DE+CD是否取得最小值？

（3）設點D為邊AB的中點，在AC上找一點T，使點T為B，D在直線AC上的投射點;

（4）在（3）的條件下，若BC=1，求TB+TD的長.

設計意圖? 對應原題的第1問，通過增設鋪墊、并關聯將軍飲馬模型帶來的最小值引導學生理解所謂投射點與最小值之間的內在聯系.

2. 變式運用，鞏固提升

例2? 如圖3，在正方形網格中，已知△ABC的頂點A，B，C三點均在格點上.

（1）利用網格中的格點，僅用沒有刻度的直尺畫出BC的中點M;

（2）在（1）的條件下，利用沒有刻度的直尺在AC上畫出點P，使AP+PM取得最小值;

（3）請用沒有刻度的直尺在AC上畫出點P，在BC上畫出點Q，使A，P在BC上的投射點Q滿足CQ=2BQ.

設計意圖? 先預設一個畫出BC中點Q的鋪墊，啟發學生后續畫出BC三等分點的思路. 另外，這樣調整畫圖順序后，也有助于學生獲得畫出點P的思路.

3. 逆向運用，拓展思考

例3? 如圖4，在Rt△ABC中，∠C=90°，AC=BC.

（1）取BC中點M，在AB上確定一點T，使點T為M，C關于AB的投射點. （簡述點T是怎樣確定的）

（2）在AB，BC邊上有點D，E，且點D為E，C在AB上的投射點，點E為A，D在BC上的投射點. 請用尺規作圖確定點D，E的位置;

（3）在（2）條件下，求DE/CD的值.

設計意圖? 對應原考題第3問，增設兩個鋪墊式問題，讓學生想到取對稱點的解題方向，并在此方向上認識問題的結構，為突破問題提供思路上的暗示.

進一步的思考

1. 深刻理解新定義的本質或問題結構特征是備課關鍵

教師在構思一道新定義考題的教學設計時，需要深入思考新定義的本質或圖形結構特征. 比如本文提供的這道模考題，新定義“投射點”的本質就是將軍飲馬模型中的最值點，也是光線反射的反射點，想清這些之后，就可圍繞與之相關的模型設計一些同類題呈現出來. 比如在“教學微設計”環節，我們預設的“求TB+TD的長”或者“使AP+PM取得最小”都是引發學生對比新定義中投射點與學生有已經驗（將軍飲馬模型）之間的聯系.

2. 鋪墊式設問給學生自主破解問題提供思路上的暗示

鋪墊式設問是這類教學微設計的關鍵所在，基于新定義考題的結構特征而設計的鋪墊問題，能讓學生在這些問題的探究之后，調動相關解題經驗，把思路引向恰當的思考方向，從而能自主獲得解題路徑.教學中我們追求“潤物細無聲”，通過一些無痕的引導或有意無意的對話與追問，可以促進學生在一些較難問題上獲得思路的自主突破，學生在解決問題之余收獲解題自信，一舉多得. 而這樣的教學預設就可以采用課前設計鋪墊式問題的做法來實現.