深入考題模型，拓展應用探析

趙艷

[摘? 要] 初中數學中的“將軍飲馬”模型在解決線段和最值問題中有著廣泛的應用. 本文從教材知識點說起，以一道考題為例，對該模型進行研究拓展，并給出線段和最值問題的教學建議.

[關鍵詞] 最值;線段;將軍飲馬模型;拓展;思想

從教材考點說起

“軸對稱”是蘇教版八年級上冊的重要內容，教材中結合生活實際對該內容進行了詳細的講解，主要是為了讓學生在感受圖形對稱美的同時理解圖形變換過程中的不變關系，并能靈活運用解決實際問題. 其中該章節最為重要的知識點是軸對稱的基本性質，它是后續線段垂直平分線性質定理研究的基礎，也是相關幾何問題研究的核心，尤其是利用其性質，結合“兩點之間，線段最短”定理進行線段和最值問題的探究活動. 在近幾年各地的中考中出現了眾多考查該知識點的考題，如常規的平面幾何題、研究線段取值的函數曲線題等.

對中考真題的探析

軸對稱的性質在拋物線問題中有著一定的應用，尤其是研究線段最值時可以采用該種轉化方式，依據軸對稱的性質可以建立起兩點直線距離的研究模型，下面探究一相關中考題.

從考題抽象模型

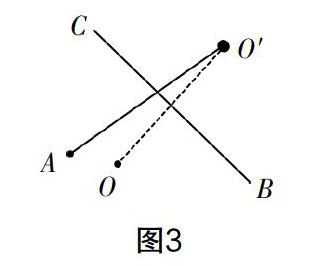
上述第（2）問求PO+PA取得最小值時點P的坐標，就是研究定點A，O與定直線l上動點P之間的線段最值. 對考題進行模型抽象，如圖3所示，在問題解答過程中采用作對稱點的方式來將關于一條直線的同側點轉化為異側點，利用軸對稱的性質來轉化線段和，借助兩點之間的線段最小值定理可以證明最小值的取值情況.

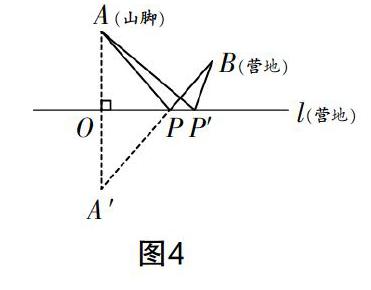
對模型進行深入探究可知該問題實際上就是對經典的“將軍飲馬”模型的變式應用，如圖4模型所示，將軍從山腳下的點A出發，到河流l處飲馬，然后再走到營地B，試問將軍應在河流的何處飲馬，所走的距離才會最短. 該問題的研究采用的就是軸對稱的建模方式，即作點A關于直線l的對稱點A′，連接A′B與l的交點就是最佳的飲馬點. 雖然出題的形式有所不同，但剖析本質所用的研究模型是一致的.

對飲馬模型的拓展

飲馬模型是研究線段最值問題的常用模型，是關于“兩定點——一定直線——一動點”的模型，是軸對稱性質和“兩點之間，線段最短”定理的綜合應用. 對于該模型我們可以進行適度的拓展，如圖5所示，l1和l2是兩條定直線，點M和N分別是直線l1和l2上的兩個動點，點P是一定點，即“一定點——兩定直線——一兩動點”模型，圖5做法就為求模型中PM+MN+NP最小值的策略：過點P分別作直線l1和l2的兩個對稱點P″和P′，根據軸對稱則有PM+MN+NP=P′M+MN+NP′=P′P″，此時線段和的最小值就為線段P′P″的長. 在歷年的考題中也有對“將軍飲馬”拓展模型的應用.

評析? 上述考題雖然增加了條件“△PCE的面積最大”，但實際上是為了確定點P的坐標，后續依然可以轉化為“將軍飲馬問題”，借助其拓展模型“一定點——兩定直線——一兩動點”，結合軸對稱性質來轉化求解. 該類問題的求解重在分析的過程，破除動定點之間的線段“屏障”，轉化為直線上的兩點模型是關鍵，模型選用正確則計算量相對較小，解題效率可獲得顯著的提升.

教學實踐建議

1. 剖析問題本質，還原考點知識

上述以拋物線為背景求解線段和的最小值，表面上屬于折線之間的長度分析，但分析解題過程可以發現，該類問題背后所承載的是學生熟悉的軸對稱性質和“兩點之間線段最短”或“垂線段最短”定理. 問題的求解實際上就是在變化的特性中提取不變特征，將“動點”與“定點”的分析轉化為“雙定點”分析，最終實現“折線”轉“直線”的目的. 因此，解題時要準確把握問題特征，對其進行本質剖析，還原問題考查原型，結合基本性質定理探索求解思路. 而在實際教學中則可以結合相關知識點來開展考題拓展，使學生深刻理解定理背后所隱含的內容，促進學生由“知識點”向“解題應用”的過渡.

2. 提煉問題模型，深層拓展發掘

對于函數與幾何的綜合題，最為關鍵的一步是對考題模型的提煉，即深入問題本質，從圖形的特征結構等方面構建模型，然后結合相關經典模型的解答策略來完成. 如上述考題從幾何線段最值問題中提煉出“動點”與“定點定直線”的研究模型，然后銜接經典的“將軍飲馬”模型來破解，模型提煉合理，則整個計算過程相對較為簡單. 而考題的研究不應止于此，畢竟考題的形式是多樣的，把握本質對模型進行適度拓展則可以確保模型的多樣化，增強模型的實用性，這對于后續的問題研究有重要意義. 因此，教學中應開展模型的提煉和拓展教學，可以從簡單的幾何模型入手，逐步變換問題的條件，使模型呈現多樣性，通過模型的分析來拓展學生的解題思維，提升解題能力.

3. 注重解題方法，發揚數學思想

上述考題的解題過程可以概括為以下三個階段：考題模型構建、數形結合分析、等效轉化求解. 即根據問題條件提煉出問題模型，然后結合相關性質定理，采用數形結合分析的方式探索，最后簡單轉化問題利用基本知識求解. 整個過程實際上是在解題思想的指導下進行的，如建模階段涉及了模型思想，分析階段涉及數形結合思想，轉化階段涉及了轉化與化歸思想，正是思想方法與基本知識的完美結合實現了問題的高效求解. 思想方法是數學的核心，是問題策略構建的指導思想，基于思想方法下的解題才是合理的，因此在解題教學中有必要滲透數學思想，引導學生理解思想方法的深層內涵，以數學思想為基礎凝練解題策略，從而達到觸類旁通的學習效果.

結束語

“將軍飲馬”模型實際上是軸對稱性質和“兩點之間，直線最短”定理的綜合，結合基本模型，從基本性質定理角度來探索線段和的最值能夠取得良好的學習效果. 知識點是固化的，但模型是可變的，把握問題本質開展模型的拓展學習對于解題思維的提升具有一定的幫助，上述模型的研究僅是一個典型例子，后續還需進一步挖掘.