單圓柱滾子包絡蝸桿傳動嚙合效率分析

王小林， 韓志， 段冬冬

（河南理工大學機械與動力工程學院，河南焦作 454000）

0 引言

滾柱包絡環面蝸桿傳動原理是將傳統環面蝸桿副中的蝸輪輪齒以回轉體（本文中以單圓柱滾子為例）代替，以期達到用滾動摩擦替代滑動摩擦，提高蝸桿副嚙合效率的目的[1]。其具有承載能力強、運動平穩、使用壽命長等特點，尤其是具有較高的傳動效率，使其顯著地區別于傳統的蝸桿傳動。

經過樣機試制與試驗，發現試驗中蝸桿副的嚙合效率與理論計算數值有較大差距[2-4]，不能夠充分發揮這種型式傳動嚙合效率高的優點。因此有必要對滾柱蝸桿傳動的嚙合效率進行理論研究。影響嚙合效率的因素有很多，包括理論分析中存在的偏差和實際應用中存在的誤差[5-6]。滾柱蝸桿副傳動實現了回轉體和蝸桿齒面接觸，改變了接觸型式，但在沿著回轉體軸線方向存在蝸桿副的相對運動速度分量[7]，接觸齒面間滑動摩擦和滾動摩擦情況復雜，增加了構建蝸桿副嚙合效率公式模型的難度。

本文以單圓柱滾子包絡環面蝸桿傳動為研究對象，利用蝸桿與蝸輪之間作用力和反作用力的關系，建立了嚙合效率公式，以此為基礎分析了摩擦因數、傳動比和滾柱半徑對蝸桿傳動嚙合效率的影響，為滾柱包絡環面蝸桿傳動的理論設計和結構優化提供了重要的參照。

1 滾柱受力分析

單圓柱滾子包絡環面蝸桿副運動的實現，是以蝸桿作為運動的輸入部件，通過蝸桿齒面和滾柱外表面接觸，帶動滾柱轉動，最終使蝸輪按照確定的傳動比運動[8-10]，如圖1所示。以滾柱外表面上的任一接觸點P0為研究對象進行受力分析，如圖2所示，坐標系及活動標架以文獻［11］中的設置為參考。

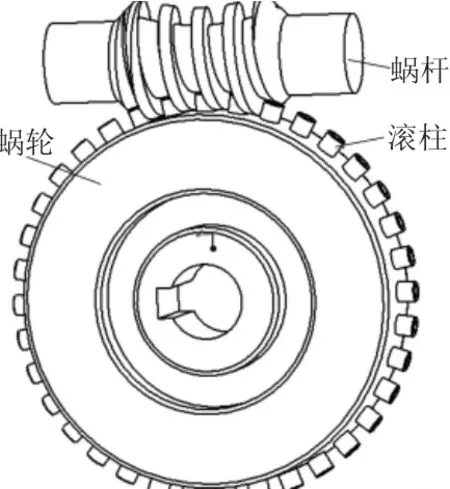
圖1 傳動原理

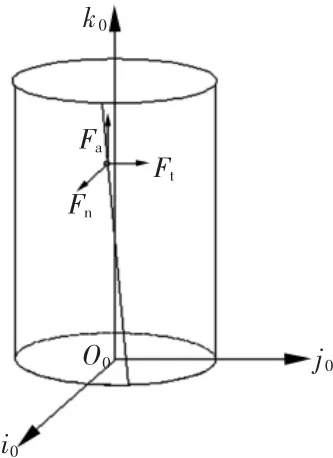
圖2 滾柱受力分析

圖2中：P0是接觸線上任意一個接觸點；Ft是接觸點在滾柱周向方向受到的滑動摩擦力；Fa是接觸點在滾柱軸向方向受到的滑動摩擦力；Fn是接觸點在滾柱法向方向受到的滑動摩擦力。

蝸桿與蝸輪的相對速度在環面蝸桿副的切平面內，在接觸點處的滾柱法向沒有分速度，所以Fa和Fτ都位于接觸點處的切平面內[12-13]。

滾柱在周向滑動摩擦力Ft的作用下，繞著軸線z2以角速度ω2轉動，故忽略其對效率計算的影響[14]。取滾柱作為研究對象，滾柱受到蝸桿作用的正壓力Fn和滑動摩擦力Ff，二者的矢量和就是接觸點受到的合力，將合力設為Fr2，Fr2=Fn+Ff；取蝸桿作為研究對象，蝸桿受到滾柱作用的正壓力Fn′和滑動摩擦力Ff′，二者的矢量和就是蝸桿受到滾柱的合力，將合力設為Fd1′，Fd1′=Fn′+Ff′。根據作用力和反作用力的關系，其中Fn=-Fn′，Ff=-Ff′。蝸桿受到的驅動力應與滾柱施加在蝸桿上的合力Fd1′大小相等，方向相反，設為Fd1：

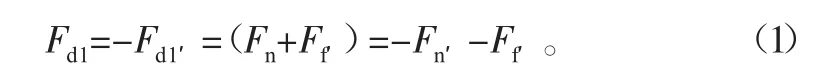
式中，Fd1是施加在蝸桿上面的驅動力。

2 嚙合效率公式

根據機械原理知識[15]可得，機械效率按照瞬時輸出功率和瞬時輸入功率比值來計算。

設蝸輪輸出效率為Pr，計算公式如下：

設蝸桿輸入功率為Pd，計算公式如下：

由蝸桿輸入功率Pd和蝸輪輸出功率Pr可得，滾柱包絡環面蝸桿傳動的理論嚙合效率η的表達式如下：

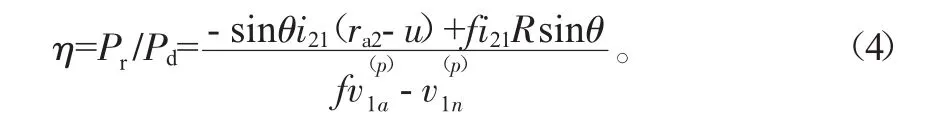
3 嚙合效率影響參數

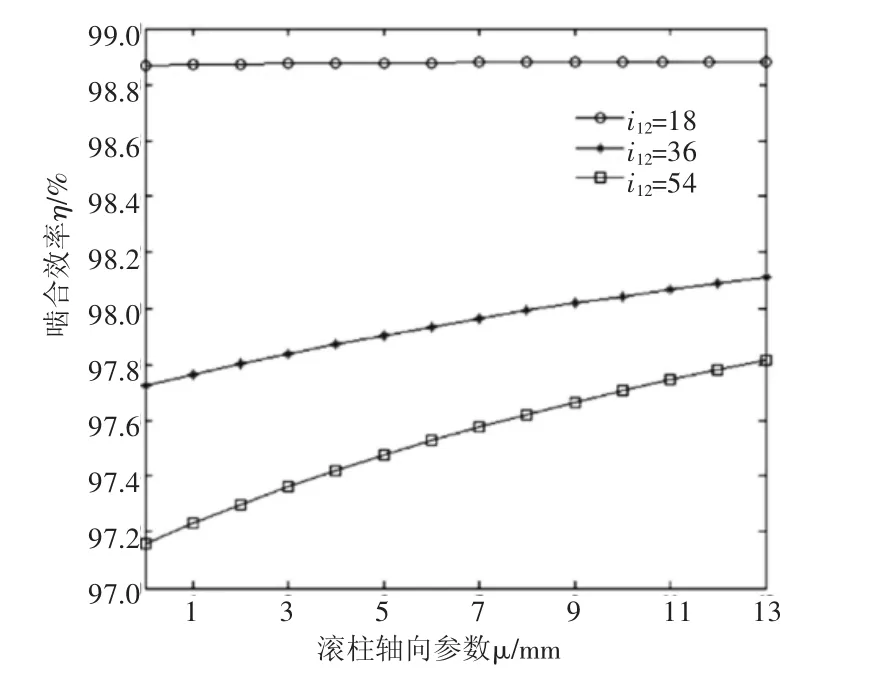
圖3 η與i12的關系

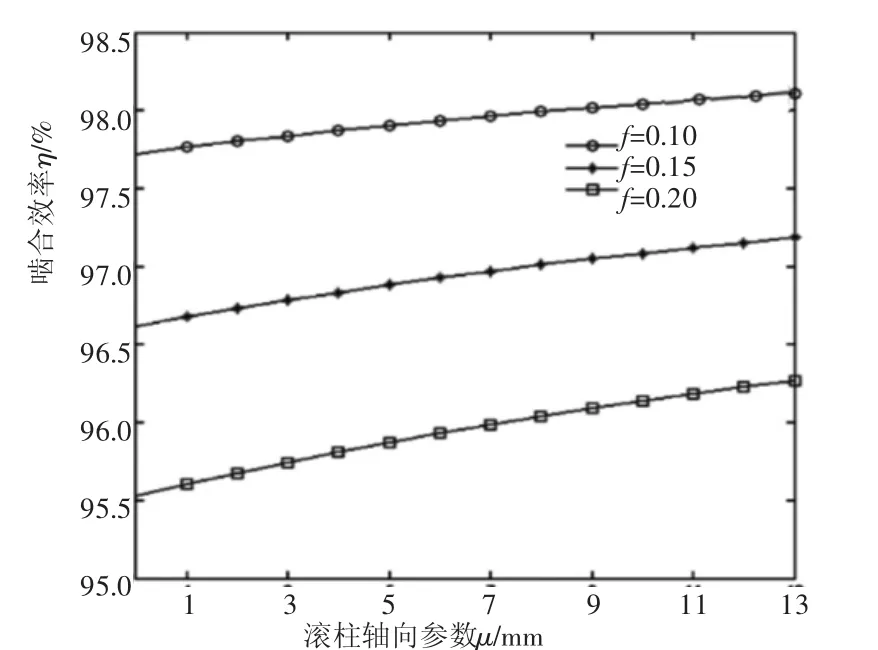
圖4 η與f的關系

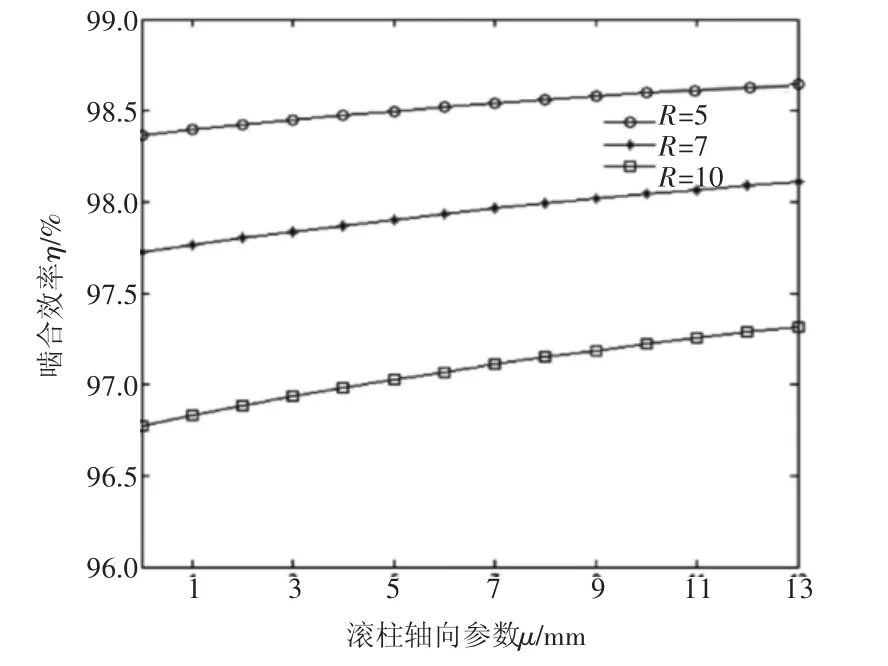
圖5 η與R的關系

由嚙合效率公式（4）可以看出，與嚙合效率有關的參數有：θ、i21、ra2、u、f、R、φ1、a。其中，ra2為滾柱齒頂所在圓半徑，a為中心距，兩者在蝸桿副運動規律確定時即為定值。當蝸輪轉角φ2=-25°時，以滾柱齒面上的接觸線為研究對象，在MATLAB中利用單一變量法作圖，它上面的嚙合效率η和傳動比i21、摩擦因數f、滾柱半徑R的關系分別如圖3～圖5所示。

綜合比較圖3～圖5發現：在滾柱軸向參數u一定時，減小傳動比i12、降低摩擦因數f、減少滾柱半徑尺寸R，會使嚙合效率升高，反之，嚙合效率下降；從滾柱柱頂到底部，嚙合效率逐漸增大，滾柱表面上嚙合效率分布不均勻。

對比圖3～圖5也可以看出，影響嚙合效率的參數中，摩擦因數所占比例最大，其次是傳動比，滾柱半徑值影響較小。當f增大0.05時，η降低幅度超過2%。因此，應保持環面蝸桿副接觸區處于良好的潤滑狀態，選擇合適的潤滑條件和潤滑方法，避免邊界潤滑和干摩擦的出現。

對于滾柱上軸向參數u=0的位置，當蝸輪轉角φ2在范圍-25°～25°內變化時，嚙合效率φ和傳動比i21、摩擦因數f、滾柱半徑R的關系分別如圖6～圖8所示。

圖6～圖8表明：嚙合效率變化以蝸輪轉角φ2=0為節點，在該點左側時，嚙合效率隨著蝸輪轉角增大而減小，在該節點右側時，嚙合效率隨著蝸輪轉角的增大而增大；在同一蝸輪轉角處，增大傳動比i12、升高摩擦因數f、增加滾柱半徑R，嚙合效率η減小。

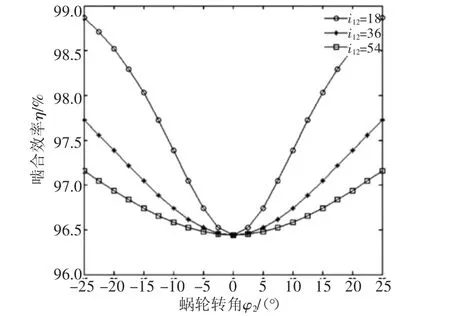
圖6 η與i12的關系

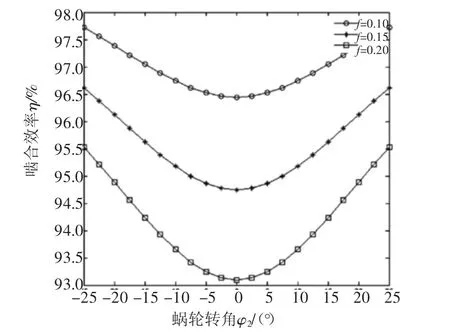
圖7 η與f的關系

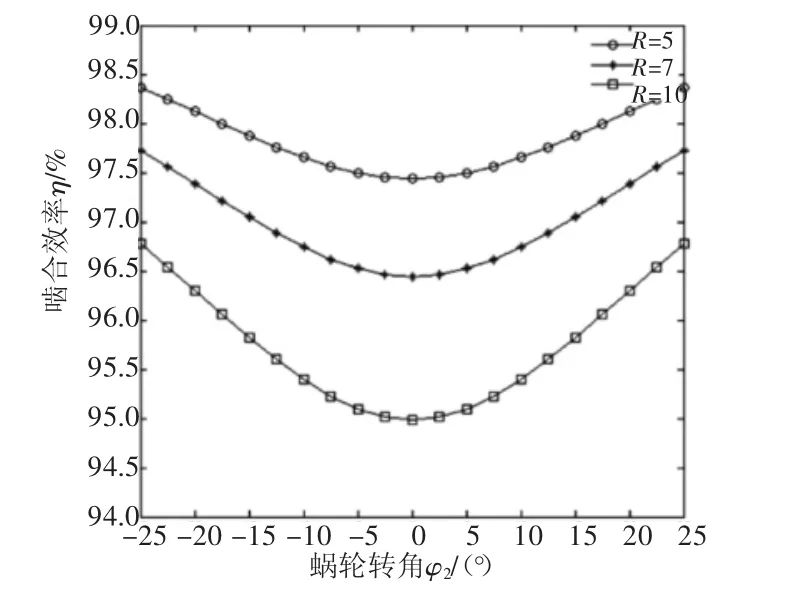
圖8 η與R的關系

由圖8得到結論：在滾柱半徑R=10 mm時，嚙合效率降低幅度已經很大，當蝸輪滾柱運動到蝸桿喉部位置時，嚙合效率與滾柱半徑R=5 mm時相比，已經降低了大約3%，因此在滿足傳動所要滿足的強度和剛度條件下，滾柱半徑值不宜過大。

上面是在蝸輪轉角φ2處于-25°～25°范圍內進行分析的，實際的生產要求蝸桿與蝸輪運動的轉角范圍比這個大許多。當滾柱與蝸桿連續嚙合傳動時，選取滾柱柱頂位置，嚙合效率η與摩擦因數f、傳動比i12和滾柱半徑R之間的關系分別如圖9～圖11所示。

由圖9、圖11可知，摩擦因數f和滾柱半徑R對嚙合效率η的作用效果相似，只能等比例放大或者縮小嚙合曲線圖，不會改變曲線的形狀，即在蝸輪某個確定轉角時，較小的摩擦因數f和較小的滾柱半徑R總是對應于較高的嚙合效率。

由圖10可知，在蝸輪轉動一周的范圍內，傳動比i12=36時的嚙合效率曲線和i12=18時的嚙合效率曲線有4個交叉點，對應的橫坐標φ2依次是φ2=0°、120°、240°和360°。

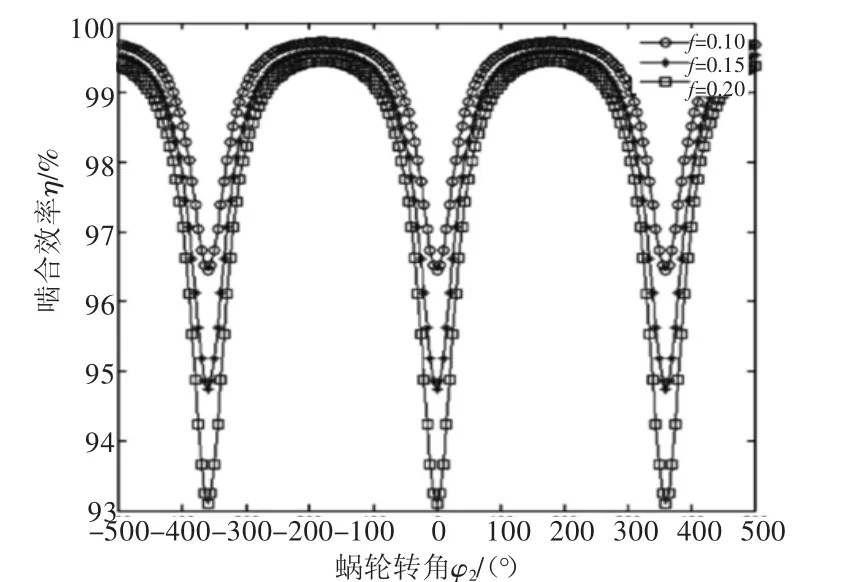
圖9 η與f的關系

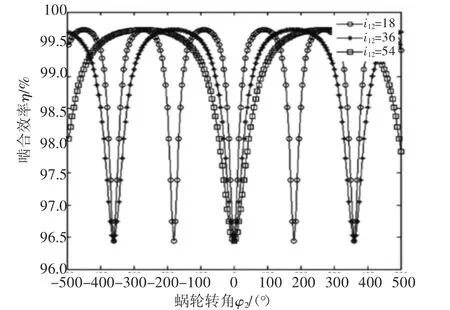
圖10 η與i12的關系

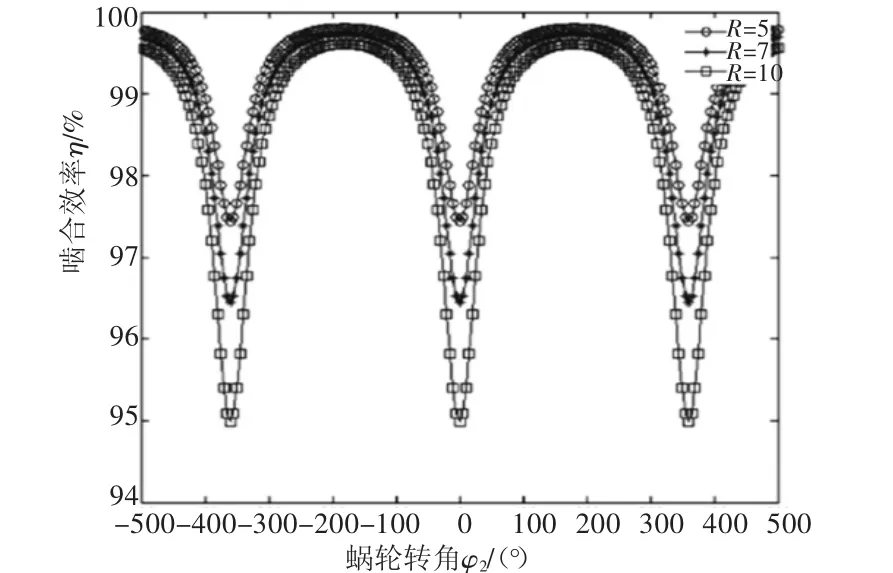
圖11 η與R的關系

在φ2=0°～120°和120°～360°范圍內，i12=18時的嚙合效率高于i12=36時的嚙合效率；當φ2=120°～240°時，i12=18時的嚙合效率低于i12=36時的嚙合效率。對于其他曲線之間的嚙合效率對比，由于嚙合效率隨著蝸輪轉速的變化曲線成“圓拱形”，所以有著類似的結論，只是嚙合效率相等點的橫坐標發生變化，即對應于不同的蝸輪轉角。

所以，比較蝸桿副嚙合效率高低時，在其他參數條件相同的情況下，對應于不同的傳動比大小，由于在不同的蝸輪轉角時刻，嚙合效率之間大小關系會發生變化，不能簡單地說某個傳動比數值時嚙合效率比另一個數值大，應當算出在確定的蝸輪運動周期內，嚙合效率在這個周期內效率和的大小，再比較對應不同傳動比時的嚙合效率。

4 結論

1）滾柱齒面上的嚙合效率分布不均勻，在滾柱底部的位置時的嚙合效率大于在滾柱柱頂的嚙合效率，從滾柱柱頂到滾柱根部，嚙合效率單調遞增。2）摩擦因數對嚙合效率的作用最大，其次是傳動比，滾柱對嚙合效率的影響效果較小，但需要保證滾柱具有足夠的強度和剛度，以傳遞蝸桿副傳動的運動和力。3）摩擦因數和滾柱半徑的變化改變嚙合效率曲線的縱向形狀，傳動比的變化使其橫向形狀改變，嚙合效率呈周期性變化。

[1] 邊輝.對滾柱包絡環面蝸桿傳動機構的一點思考[J].機械工程師,2010(10):136-137.

[2] 楊玉虎,沈煜,張策,等.環面蝸桿類零件實體建模研究[J].天津大學學報(自然科學與工程技術版),2004,37(6):471-474.

[3] 劉新華.無側隙雙滾柱包絡環面蝸桿傳動減速器的設計與分析[D].成都:西華大學,2010.

[4] 陳尚友.無側隙滾柱包絡端面嚙合蝸桿傳動建模與研究[D].成都:西華大學,2015.

[5] 張寶鋒,崔亞輝,劉凱,等.漸開線圓柱直齒輪結構參數對嚙合效率的影響分析[J].機械強度,2015,37(1):122-127.

[6] 許立忠,聞巖.滾錐包絡環面蝸桿傳動效率研究[J].潤滑與密封,2001(4):10-12.

[7] 沈煜,楊玉琥,楊一平.滾柱包絡環面蝸桿傳動的運動學分析[J].機械設計,2003,20(6):38-40.

[8] 王進戈,張光輝.滾錐包絡環面蝸桿傳動的理論研究與參數優化[J].重慶大學學報,1992,15(2):58-64.

[9] 王其超,劉健.滾動式回轉面包絡點嚙合環面蝸桿傳動的點嚙合原理[J].大連工業大學學報,2000(4):281-285.

[10] 張永強.無側隙雙滾柱包絡環面蝸桿傳動的幾何特性及研究[D].成都:西華大學,2014.

[11]洪雷.無側隙雙滾子包絡環面蝸桿傳動的理論研究[D].成都:西華大學,2008.

[12] 柳在鑫,王進戈,張均富,等.交錯軸雙滾子包絡環面蝸桿傳動嚙合分析[J].四川大學學報(工程科學版),2012,44(4):221-225.

[13]王凱,王進戈,鄧星橋.無側隙雙滾子包絡環面蝸桿傳動的嚙合性能分析[J].機械傳動,2009,33(6):12-15.

[14]趙韓,梁錦華.蝸桿凸輪機構的嚙合原理及幾何特性分析[J].合肥工業大學學報(自然科學版),1985(1):63-75.

[15] 孫恒,陳作模,葛文杰.機械原理[M].北京:高等教育出版社,2006:68-70.