非圓齒輪數控滾切加工的現狀及發展趨勢

李先平， 舒啟林， 李歡歡

（沈陽理工大學機械工程學院，沈陽 110159）

0 引言

齒輪是機械裝備中最常用的一種傳動零件，非圓齒輪是圓柱齒輪的一種變形，兼具了齒輪和凸輪的優點，不僅有穩定的傳動比，還能實現非勻速傳動，主要運用于輕工業[1]、機床制造業及儀器儀表業。它的概念最早于二十世紀初期提出，迄今已有一百多年的歷史，但由于它的設計和計算復雜、難以加工的特點使其發展停滯。隨著計算機技術的發展，使非圓齒輪的理論再次被提出。現階段對非圓齒輪的研究主要集中在利用計算機技術進行非圓齒輪節曲線的設計、非圓齒輪齒廓生成以及數控加工程序的生成和仿真加工等方面，并逐步實現整個過程的全自動化。另外隨著CAD/CAM技術的日趨成熟，可以使抽象的數學式變成直觀的圖形。

1 非圓齒輪加工方法

早期加工非圓齒輪加工方法有靠模法、近似滾切法，但由于加工精度不高、效率低逐漸被淘汰[2]。現在對非圓齒輪加工的研究主要集中在數控滾齒、數控插齒及數控銑齒和線切割技術。

1.1 數控插齒

非圓齒輪的加工最早是通過插齒加工實現的[3]，插齒被廣泛用于非圓內、外齒輪的加工，并具有較高的精度。徐曉俊[4]提出一種基于節曲線離散點的通用非圓齒輪數控插齒程序設計方法，通過各離散點計算出刀具和工作臺的離散位置，通過計算機輔助生成加工程序。楊世平[5]根據非圓齒輪節曲線方程推導出數控插齒機五軸聯動數學模型。李波[6]利用非圓齒輪的節曲線法向向量得到基于包絡模型的非圓內齒輪插齒加工三軸聯動模型，該模型簡化了自動編程的計算量。李建剛、吳序堂等[7]提出了一種判斷非圓齒輪任意齒廓是否發生根切的精確方法，提高了數控插齒加工非圓齒輪的質量。

1.2 數控銑齒

李宇鵬、田斌等[8]根據非圓帶輪節曲線切線的極坐標理論建立了銑削加工非圓齒輪的點位計算模型，并在坐標鏜床上采用分度頭分齒銑切非圓帶輪，為非圓齒輪銑削加工奠定了基礎。孔德勇[9]利用斷續展成法進行數控銑削加工，加工時主要有四種運動：銑刀繞自身軸線轉動、銑刀的軸向移動、銑刀軸心與非圓齒輪齒坯中心距移動和回轉工作臺的轉動。由于數控銑齒加工非圓齒輪的效率較低，故該方法使用較少。

1.3 數控線切割

張生余、金秀石[10]利用圓柱齒輪的嚙合原理找到齒面法線與節圓焦點跟齒面之間的幾何關系計算出每個齒的齒廓坐標，然后利用計算機打印出穿孔帶，在線切割機床上實現非圓齒輪加工。李建剛、吳序堂等[11]將非圓齒輪的齒廓計算轉化成求非圓齒輪節曲線的全部齒廓數據，可快速精確計算非圓齒輪齒廓。戴有華、胡赤兵等[12]利用三維軟件實現非圓齒輪建模，然后利用軟件仿真模塊生成數控線切割加工代碼。

1.4 數控滾齒

為實現高硬度、大模數、大齒寬的非圓齒輪，戴有虎[13]根據非圓齒輪嚙合原理建立了滾切加工非圓齒輪的數學模型，為非圓齒輪滾切加工的研究奠定了基礎。其后有大量學者進行了非圓齒輪滾切加工的研究，其主要研究方向有：自動編程，工藝庫，加工誤差。

2 非圓齒輪滾切的數控系統

2.1 滾切數學模型

譚偉明、胡赤兵等[14]通過對非圓齒輪節曲線分析，建立了滾齒加工各運動軸聯動的數學模型，為實現滾齒加工自動編程奠定了基礎。張國政等[15]推導了滾切加工直齒非圓齒輪的數學模型。滾切過程中，滾刀節線與齒輪節線相互保持純滾動，其滾切示意圖如圖1所示。

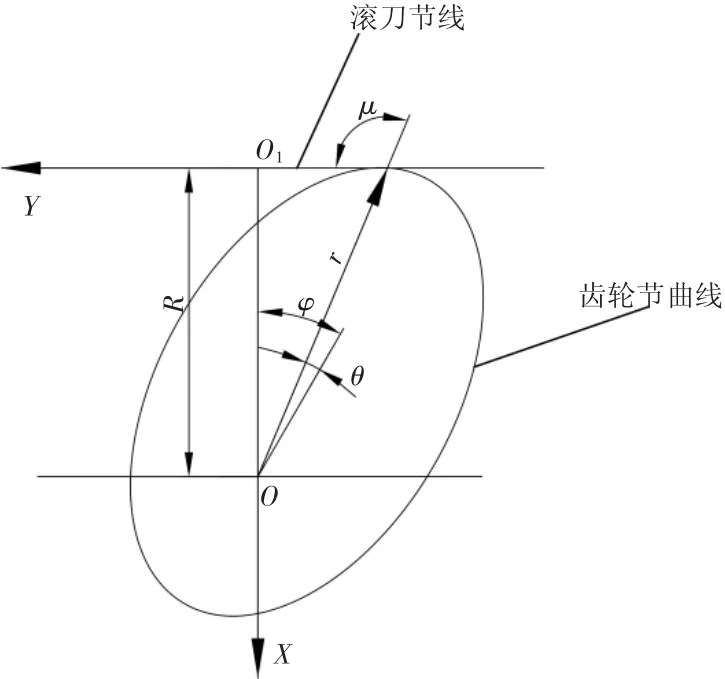
圖1 直齒非圓齒輪滾切示意圖

直齒非圓齒輪的節曲線表達式記為r=r（θ），它是以極角θ為自變量的函數，通過微分幾何原理可以得滾切運動模型：

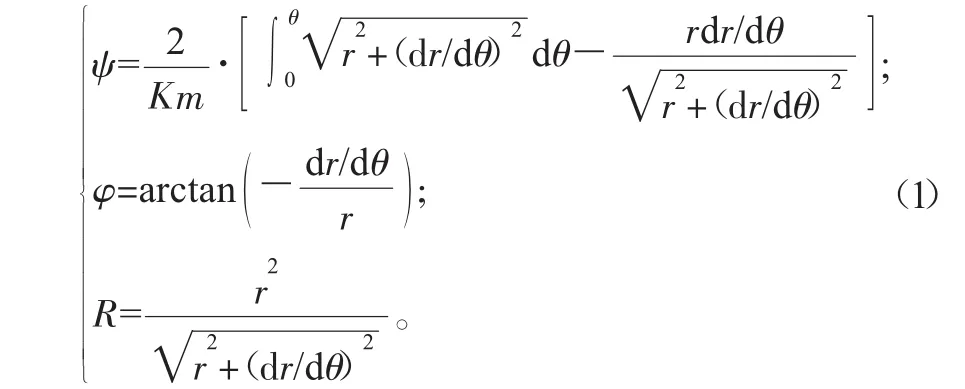
式中：ψ為滾刀轉角；K為滾刀頭數；m為滾刀模數；φ為工件轉角；R為滾刀軸線與工件回轉軸線的距離。

由滾切模型可以看出，滾切非圓直齒齒輪需要三個基本運動：工件轉動（角速度ωc）、刀具轉動（角速度ωb）及工件與刀具軸線間的相對位移（線速度vy）。在實際加工中，為了加工整個全齒寬，需要刀具沿工件軸線方向進給運動。

丁和艷[16]建立了非圓斜齒輪數控滾切加工的運動模型。加工斜齒非圓齒輪時，需要五個基本運動：工件轉動（角速度ωc）、刀具轉動（角速度ωb）、工件與刀具軸線間的相對位移（線速度vy）、刀具沿工件軸線方向進給運動（vz）及滾刀沿工件軸向的差動運動（Δωc），它們均是以極角θ為自變量的函數。

2.2 滾切加工方案

在進行非圓直齒輪滾切加工時考慮三個基本運動，則滾切加工方案有：滾刀恒速、工件恒速及工件等極角恒速。

1）滾刀恒速。即ωb為固定值，則通過數值積分法得運動模型，其中工件角速度ωc和刀具軸線間的相對位移的線速度vy均是與ωb有關的函數:

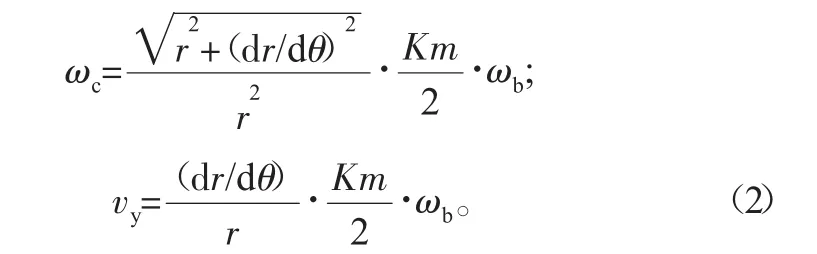
當滾刀的切削功率較大時，宜采用此方案。

2）工件恒速。即ωc=固定值，則ωb、vy均是與ωc有關的函數:

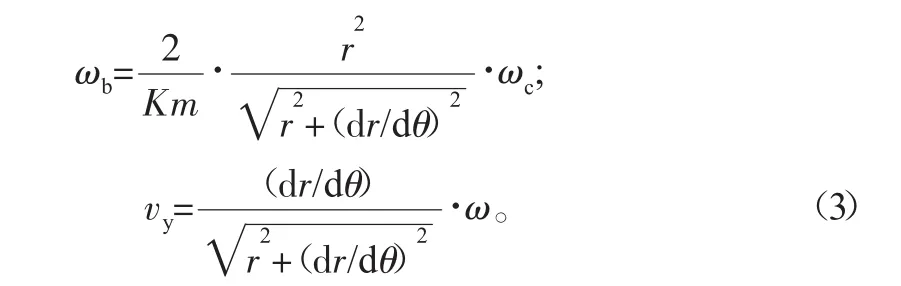
當滾刀的切削功率較小時，宜采用此方案。

3）工件等極角速度。即dθ/dt=固定值，通過數值微分法則可得相關運動模型:

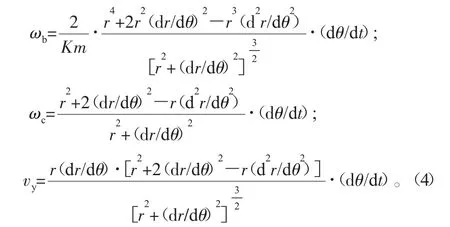
此方法的數值計算最簡單，但ωb、vy和ωc三者無一恒定，加大了控制難度，且該方案的切削不均勻，因此一般不采用該方案。

2.3 數控滾切插補算法

傳統的非圓齒輪滾齒加工是通過齒輪控制各軸進行關聯運動，文獻[17]對各軸聯動方案進行了研究。數控滾切加工非圓齒輪插補算法是數控系統的核心，它是影響機床加工性能的重要因素。非圓齒輪滾切的插補方法有三種：等極角插補，等弧長插補，三樣條曲線插補。

1）等極角插補。根據精度要求將非圓齒輪的節線分成若干極角相等，弧長不一定相等的曲線，求出若干節點。將合格節點連成一系列首尾相連的折線，則此折線近似替代非圓齒輪的節曲線。再將這些若干節點帶入滾切數學模型中，就能求出各運動軸的增量。此方法是基于直線插補的算法，為了保證加工精度，需要節點足夠多，導致計算量增加。另外，此插補方法加工出的非圓齒輪齒距不均勻，在極徑大處齒距大，極徑小處極徑小。

2）等弧長插補。根據精度要求將非圓齒輪的節曲線分成若干弧長相等的曲線，求出這些曲線的端點值，再將這些節點連成一系列折線逼近非圓齒輪節曲線，再按等直線插補。此加工方法同樣基于直線插補，加工出的齒輪齒距分布均勻。但在各相鄰折線交接處一階、二階導數不連續，因此加工過程中各運動軸的運動方向和受力會產生突變，引起機床振動，降低加工質量。

3）三樣條插補。吳焱明[18]最先提出用三樣條曲線擬合非圓齒輪的節曲線，并進行插補。此方法可以在一段加工程序內通過連續插補完成，避免了運動軸的方向及受力突變，減少了振動。田芳勇[19]根據曲線插補提出了三次B樣條曲線自適應插補算法，該算法在保證加工要求同時，保證運動軌跡每一瞬時的速度和加速度在系統允許范圍內，提高加工精度。此方法與前兩種插補方法相比，插補的計算量大，對計算機處理器要求較高。

2.4 自動編程系統

數控滾切加工非圓齒輪關鍵在于編制數控程序，靠手動編程難以實現非圓齒輪滾切加工，因此滾切加工的研究主要針對自動編程。胡赤兵[20]通過非圓齒輪的滾切運動模型建立了滾切加工非圓齒輪的自動編程系統。用戶只需要輸入一些非圓齒輪的基本參數、滾刀參數、工藝參數和機床參數等，系統就能自動生成加工代碼。系統主要包括：參數輸入模塊、工藝處理模塊、后置處理模塊以及信息管理模塊。

3 非圓齒輪滾切加工的工藝

3.1 切削參數

滾切加工的切削參數主要考慮刀具材料、工件材料、齒輪模數、機床特性和其它。現在滾切非圓齒輪的切削參數大部依靠經驗確定，沒有針對非圓齒輪滾切的切削參數表。有學者曾以圓柱齒輪切削參數優化設計理論為基礎[21]，建立了非圓齒輪的切削參數優化模型，這為切削參數優化設計提供了新方向。

3.2 對刀計算

非圓齒輪是對號嚙合的，主動輪與從動輪在同一個極徑處相差1/2個齒距，因此加工時存在對刀起始點問題。早期的對刀是依靠工人經驗進行，有很大的齒形誤差。田芳勇[22]提出了光電編碼器對刀，該方法是在滾刀旋轉軸和工作臺上分別安裝一個光電編碼器，并在滾刀某一位置設置零位，在工作臺某一位置設置零位并與齒輪的起始位置重合。開動機床后，工件和滾刀均以一定的速度旋轉。此時系統開始檢查光電編碼器的脈沖信號，當同時檢測到齒坯軸和滾刀軸上光電編碼器上的零位信號后完成對刀。

3.3 軸向躥刀

在多周聯動滾切加工非圓齒輪時，非圓齒輪加工范圍如圖2所示。

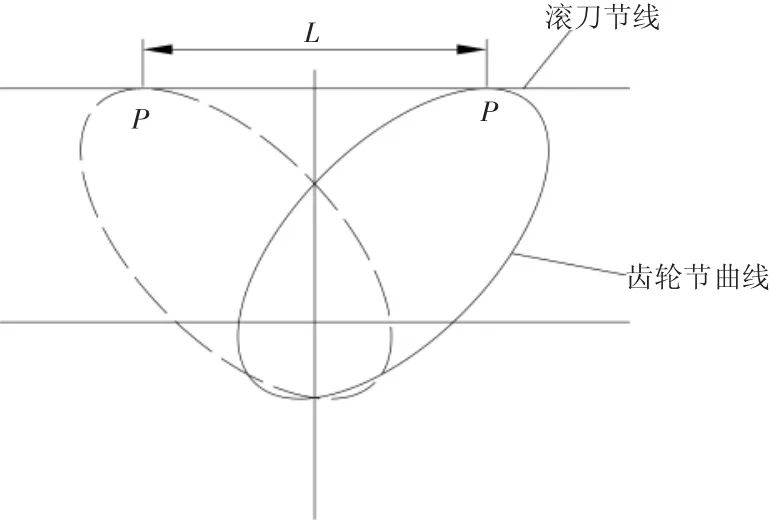
圖2 滾刀運動區域

非圓齒輪繞運動中心轉動時，最大運動區域長度為L，當L大于滾刀長度時，將會出現無法加工的情況。綜合考慮滾刀受不均勻載荷和滾刀的軸向加工范圍不足的情況需要進行軸向躥刀。夏鏈等[23]通過對滾切運動分析找到了軸向躥刀方案。

3.4 走刀方式

走刀方式主要有逆滾、順滾和軸向逆順滾，不同的走刀方式有不同的刀軌點位計算方法。目前大部分滾齒加工都采用逆滾方式進行。加工時采取何種走刀方式需要綜合考慮機床參數、刀具參數、工件材料、加工精度以及加工效率等相關因子。

4 非圓齒輪滾切加工的加工誤差

非圓齒輪沒有確定的精度標準，都是根據傳動要求和使用者要求確定精度的。現在對非圓齒輪的精度研究主要集中在對非圓齒輪周節累積誤差、齒廓誤差和節曲線誤差上。滾切加工非圓齒輪的加工誤差除了理論誤差外，還有工藝系統的誤差。

4.1 滾刀誤差

滾刀誤差主要分為滾刀制造誤差和滾刀安裝誤差，文獻[24]分析了滾刀制造誤差對滾切加工影響，并建立了滾刀制造誤差對齒廓誤差影響的誤差計算公式。滾刀的安裝誤差是指滾刀安裝在機床刀桿上之后形成的徑向跳動誤差、軸向歪斜量及軸向竄動，它們將使滾刀切削刃在一轉中周期的產生多切或少切，因而引起被加工齒輪齒廓誤差。

4.2 機床誤差

機床誤差主要有機床導軌誤差、傳動原件制造安裝誤差和電壓波動產生的轉速變化。齒輪在滾切加工時，輪齒的寬度是滾刀作垂直進給運動加工形成的，當刀架導軌和工作臺回轉軸線有傾斜角度時，就會使被切齒輪在齒寬方向產生原始齒廓位移誤差[25]。滾切時由于傳動件不可避免有制造、安裝誤差，會使滾刀與被加工齒輪間的相對位置發生變化，因此會將誤差直接反映在被加工件上，引起轉角誤差。文獻[26]提出用轉角誤差和傳動鏈的

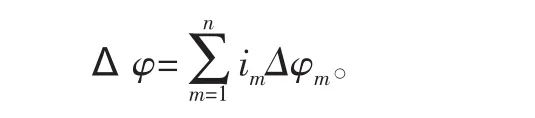
式中：Δφ為總傳動鏈誤差；im為傳動鏈第m和原件至傳動鏈末端的傳動比；Δφm為傳動鏈第m個元件的轉角誤差。

4.3 齒坯誤差

實踐證明，齒坯的制造誤差會使齒輪在滾齒機上的安裝偏心，是造成被加工齒輪周節累積誤差主要原因之一[27]，另外齒坯誤差還導致了嚙合線誤差。非圓齒輪齒坯誤差導致的嚙合線誤差計算比圓柱齒輪的計算更復雜，現今沒有較好的計算方式。

5 非圓齒輪滾切加工發展趨勢

1）插補算法多樣性。為適應不同的傳動需求，非圓齒輪節曲線也朝著多樣性發展，因此要求滾切非圓齒輪的系統能更廣范圍適應不同的非圓齒輪。非圓齒輪的節曲線不同會使運動軸的運動量產生變化，因此需要研究更多的插補算法，以適應不同類型的非圓齒輪。隨著計算機技術的不斷發展，系統承載能力更強，因此可以實現更多的復雜運算。

2）獨立的誤差補償。現在對滾切非圓齒輪誤差補償大部分是按照圓柱齒輪誤差補償進行計算的，但非圓齒輪在原理上就與圓柱齒輪不同，因此需要考慮更多的誤差影響因子，綜合考慮工藝系統、控制系統、升降速、動態影響等因素，建立滾切非圓齒輪的誤差補償系統。

3）工藝優化。現今對滾切加工非圓齒輪的加工工藝研究還很少，有相關的研究都近似于圓柱齒輪的工藝。非圓齒輪滾切加工時不可避免地會出現升降速，會引起機床振動，降低加工質量，欲實現高速高效的加工，需要優化滾切加工工藝。隨著優化科學在制造業中的廣泛運用，滾切加工非圓齒輪的工藝優化找到了新的方向。

4）統一檢測標準。非圓齒輪節曲線復雜多樣，導致了檢測標準多樣。現在對非圓齒輪的檢測標準都是根據傳遞運動的準確性和客戶要求進行建立的，并沒有像圓柱齒輪那樣有一套統一的檢測標準，因此為滾切非圓齒輪機床的研究帶來了困難。因此有必要制定統一的非圓齒輪檢測標準。

6 結論

從滾切加工非圓齒輪的加工數控系統構建方法、加工工藝、加工誤差分析三個方面較為系統地介紹了現有研究成果，重點突出插補計算、滾切方案的研究成果，指出要建立統一檢測標準以推進非圓齒輪的推廣；要發展更多的插補算法；要采用機械優化理論對非圓齒輪滾齒工藝進行優化；要建立完整獨立的非圓齒輪插補系統。傳動比來表示最終運動誤差：

[1] 李寶妮,張迎春.非圓齒輪的應用及其發展動向[J].機床與液壓,2008,36(4):286-288.

[2] 魏周宏.非圓齒輪加工[J].機械研究與應用,1997(4):23-24.

[3] 李福生.非圓齒輪與特種齒輪傳動設計[M].北京:機械工業出版社,1983.

[4] 徐曉俊,李華忠.非圓齒輪數控插齒加工程序的計算機輔助設計與仿真技術[J].機械傳動,1996(4):1-9.

[5] 楊世平.非圓齒輪數控滾齒與插齒加工的自動編程系統開發[J].組合機床與自動化加工技術,2008(1):84-88.

[6] 李波,何君,鄭方焱,等.非圓齒輪三軸聯動插齒加工技術研究[J].中國機械工程,2016,27(11):1455-1460.

[7] 李建剛,吳序堂,李澤湘.基于插齒數值計算模型的非圓齒輪根切分析[J].農業機械學報,2007,38(6):138-142.

[8] 李宇鵬,田斌.非圓帶輪齒形加工方法的研究[J].機械工程師,1997(2):1-2.

[9] 孔德勇.非圓齒輪數控銑齒加工自動編程系統的研究[D].蘭州:蘭州理工大學,2011.

[10]張生余,金秀石.非圓齒輪線切割加工數控程序計算機輔助設計研究[J].機械工業自動化,1991(2):10-13.

[11] 李建剛,吳序堂,毛世民,等.非圓齒輪齒廓數值計算的研究[J].西安交通大學學報,2005,39(1):75-78.

[12] 胡赤兵,孔德永,張敏,等.非圓齒輪的實體建模方法與線切割加工仿真[J].蘭州理工大學學報,2011(4):38-42.

[13]戴有虎.數控滾齒機加工非圓齒輪實例[J].制造技術與機床,1987(8):21-25.

[14] 譚偉明,胡赤兵,冼偉杰,等.非圓齒輪滾切最簡數學模型及其圖形仿真[J].機械工程學報,2001,37(5):26-29.

[15]張國政,韓江,劉有余.高階橢圓齒輪的滾齒加工方法及理論[J].計算機集成制造系統,2014,20(5):1106-1113.

[16]丁和艷.非圓斜齒輪數控滾切加工關鍵技術研究[D].蘭州:蘭州理工大學,2005.

[17]陳興云,李占賢.非圓斜齒輪數控滾齒加工聯動控制方案研究[J].工業技術與職業教育,2014(1):12-14.

[18]吳焱明,王治森.非圓齒輪數控滾齒的一種插補方法[J].組合機床與自動化加工技術,2005(8):78-79.

[19]田芳勇.非圓齒輪數控滾切加工理論與自動編程系統研究[D].蘭州:蘭州理工大學,2011.

[20]胡赤兵,余亮.非圓齒輪數控滾齒加工的參數自動編程系統[J].機械設計與制造,2010(2):168-169.

[21] 鞏麗,張根保,黃強,等.滾齒切削參數多目標優化系統設計[J].制造技術與機床,2006(2):76-79.

[22] 田芳勇,胡赤兵,姜衍倉.非圓齒輪滾齒加工的一種自動對刀方法[J].蘭州理工大學學報,2010,36(4):41-43.

[23]XIA Lian,LIU Youyu,LI Dazhu,et al.A linkage model and applications of hobbing non-circular helical gears with axial shift of hob[J].Mechanism&Machine Theory,2013,70(6):32-44.

[24] 嚴慧萍,胡赤兵,劉立美.直齒非圓齒輪滾齒加工誤差的研究分析[J].機械傳動,2007(4):18-20.

[25]陳興云,李占賢.非圓齒輪數控滾齒加工誤差分析[J].工業技術與職業教育,2014(3):7-9.

[26] 胡赤兵,劉浩,苑明杰,等.非圓齒輪加工及使用誤差分析[J].蘭州理工大學學報,2013,39(5):32-36.

[27] 王亞洲,胡赤兵,鄔再新,等.非圓齒輪齒距誤差分析研究[J].華中科技大學學報(自然科學版),2013,41(6):7-10.