基于趨勢分析的間歇過程異常工況超早期報警研究

胡瑾秋， 郭 放， 張來斌

(中國石油大學 油氣資源與工程國家重點實驗室 機械與儲運工程學院， 北京 102249)

間歇過程具有靈活多變的特點，適用于小批量、高附加值、多品種的工業要求，在精細化工生產中得到廣泛應用[1]。間歇過程反應復雜，具有多時段特性，過程參數相關關系隨操作進程呈周期性的階躍變化，僅通過分布式控制系統(Distributed control system, DCS)監測參數是否超出閾值范圍并不能有效地判斷系統運行情況[2]。參數的變化趨勢是判斷階躍變化中工況是否異常的重要指標，階躍變化過程中，若參數變化速率控制不當，極易出現飛溫、飛壓等危險情況，造成嚴重后果[3]。

目前國內外對于化工間歇過程的研究多集中于多時段工況監測[4]，1994年首次提出針對間歇過程的不同子時段，采用多向主元分析(Multiple principal component analysis, MPCA)逐個建立監測模型。郭小萍等[5]提出基于滑動窗口的多時段主元分析(Principal component analysis, PCA)建模方法，解決了短期內難以取得理想數據的問題。常玉清等[6]提出一種改進的多時段MPCA間歇過程監測方法，根據不同子時段主成分特性的不同對間歇過程進行劃分，再利用MPCA方法實現各個子時段的在線監測，但該方法需要對各個時段的劃分有一定的先驗知識。王靜等[7]提出一種主元分析-多方向高斯混合模型(Principal component analysis-multiple Gaussian mixture model, PCA-MGMM)，先采用PCA對數據降維，在低維空間中用GMM對得分向量訓練，將局部概率指標融合為全局概率監控指標，該方法不需要模型的先驗知識。這些方法需要將過程數據劃分成若干個階段逐一建模，并假設各個階段服從高斯分布[8]，不僅計算復雜，而且在實際過程監測中實時性差。為了更好地實時監測工況，袁彬等[9]在3σ準則的基礎上提出一種浮動報警閾值的方法，根據系統的危險狀況，建立一級和二級浮動報警值，與固定報警閾值相比，能夠及時有效地發出警報。朱海等[10]將3σ準則應用于自適應小波閾值的選取，能夠有效地區分海洋背景噪聲和磁目標信號，剔除異常值，使小波閾值降噪效果更好。但是3σ準則成立的條件仍是假設數據服從高斯分布，不適于階躍變化過程。最小二乘法[11-13]作為常用的數據擬合方法，可以簡便地求得未知數據，并使求得數據與實際數據之間誤差的平方和最小。筆者提出一種基于最小二乘法的擬合-微分-再微分的趨勢分析方法，通過擬合-微分之后過程參數的一階變化率進行間歇過程多時段工況識別，針對階躍變化過程，利用二次微分對參數一階變化率的變化快慢分析，結合滑動窗算法，實現實時的間歇過程異常工況超早期報警。

1 基于最小二乘的趨勢分析原理

最小二乘法(Least-squares，LS)是根據“使偏差平方和最小”的原則來選取擬合曲線y=f(x)。利用最小二乘法解決問題需要兩個步驟：根據已知數據確定f(x)的具體形式；按照最小二乘的原則求得最小二乘解。經常采用的最小二乘多項式方程形式為：

f(x)=anxn+an-1xn-1+…+a1x+a0

(1)

式(1)為n次多項式擬合形式。最小二乘法的目的就是要確定ai，并且是各個點的偏差δi平方和最小。將m對數據(xi,yi)代入式(1)中，得到如下方程：

(2)

將式(2)轉換成矩陣的形式，求得矩陣的唯一的一組最優近似解，使得偏差δi的平方和最小，從而求得最小二乘擬合多項式。

2 基于趨勢分析的超早期報警方法

2.1 工況識別

假設滑動窗口長度L是曲線擬合需要的數據長度，步長D是一次擬合數據更新時窗口添加和丟棄的數據長度。滑動窗口的選取對于最小二乘擬合的準確度非常關鍵。滑動窗長度太小，擬合曲線與實際趨勢不匹配；長度太大，計算量大，擬合速率慢。由于間歇過程中參數變化頻繁，故選取較小窗口長度。取當前時刻前L個數據作為擬合所需數據，記為X0∈RL0×m，m為過程變量個數，L0為初始擬合數據長度，每隔步長D對擬合數據進行一次更新Xk∈RLk×m，k為數據的更新次數。Lk為第k次更新訓練數據的長度。其中：

(3)

選取歷史數據中正常樣本數據根據公式(2)進行最小二乘曲線擬合，求出長度為L的數據的最佳擬合函數，并進行一階、二階微分計算得到參數的一階和二階微分方程。一階方程式反映參數變化率υ的情況，用來識別工況處于的階段；二階方程式反映參數的二階變化率γ的情況，用來判斷參數在某一工況下是否出現過快或過慢變化。

間歇過程工況大致可分為3個階段：上升階段、反應階段和下降階段。假設上升階段中參數X的值為α，一階變化率為υ。根據參數和一階變化率的數值區間，判別工況的運行階段。3個階段的參數X和其變化率υ的取值范圍如表1所示。

2.2 參數超早期報警

所謂超早期報警，即在異常發生的早期就發出警報，提前時間應在5 min以上。確定工況處于上升階段或下降階段后，采取擬合、微分、再微分的方法，計算參數X和參數的二階變化率γ的取值區間。每個階段分為2種趨勢：穩定趨勢和不穩定趨勢。不同趨勢下參數X和參數的二階變化率γ的取值范圍如表2所示。

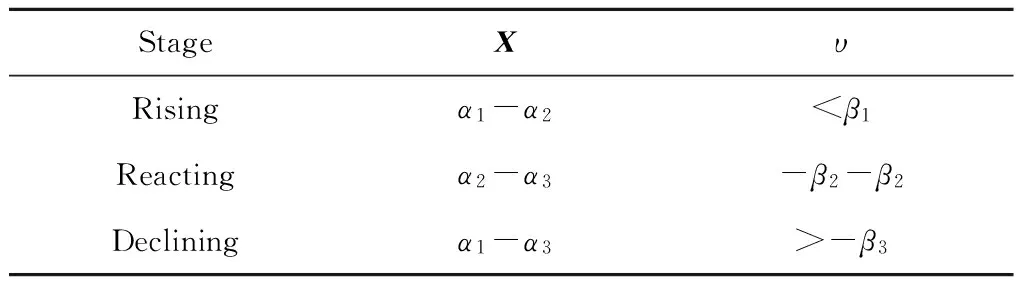
表1 參數X和一階變化率(υ)的取值區間Table 1 The range of values for parameters X and first order derivative (υ)

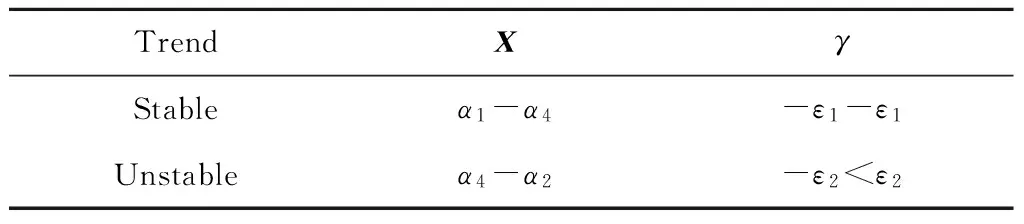
表2 參數X和二階變化率(γ)的取值區間Table 2 The range of values for parameters X and its second order derivative (γ)

數據擬合之后通過與表2中的取值范圍比較，判斷是否處于相應的區間內，若在區間范圍內，則參數變化正常，否則，參數變化異常。整個工況結束后，將3個階段的數據擬合，并進行一階、二階微分求導，得出表1和表2中的各個參數的取值區間。隨后將最大值和最小值保存到樣本庫中，并與相應的樣本庫中的數據比較，選取樣本庫中的最大值和最小值作為最新的控制限。根據表1判斷間歇過程工況階段，識別為上升階段或者下降階段，進行變化率監測。利用最小二乘法對當前T時刻長度為L的實時數據擬合，微分計算后與表2中的取值范圍比較，判斷是否處于相應的區間內，若在區間范圍內，則參數變化正常；否則，參數變化異常，發出報警信號。

3 實施步驟

針對化工間歇過程工況識別以及階躍變化報警監測的問題，提出基于最小二乘的趨勢分析方法，步驟如下：

步驟1：選取間歇過程中存在階躍變化的監測變量的10組不同時長的正常歷史數據作為訓練樣本。間歇過程中參數變化范圍大，剔除數據中離群點會忽略部分正常生產過程信息，降低報警準確度，因此，不對歷史數據進行預處理。依據公式(1)對歷史數據利用最小二乘法進行多項式擬合，求得擬合后的方程f(x)，并畫出參數擬合曲線；

步驟2：根據工藝操作要求和步驟1中得到的擬合曲線趨勢，對間歇過程的各個工段進行劃分，分為上升階段、反應階段和下降階段，并確定各個階段中參數X的取值區間；

步驟3：對歷史數據進行一階微分求導，畫出參數一階變化率的曲線。根據步驟2中劃分的各個工段的參數數值，確定各個工段的參數一階變化率υ的取值區間；

步驟4：選取間歇過程中工藝操作較危險的階躍變化階段，對該段的數據進行再微分處理，畫出參數的二階變化率γ的曲線。根據二階變化率的大小，將該階躍變化階段劃分成穩定階段和不穩定階段。穩定階段為參數在這個階段保持較穩定的速率上升或下降，不穩定階段為參數在這個階段呈現出不太穩定的上升或下降。結合該工段的參數取值，確定穩定階段和不穩定階段的參數二階變化率γ取值區間；

步驟5：由于間歇過程參數波動較大，窗體大小和步長不宜過大。選取窗體大小為400～500 s，步長為5～10 s。對在線數據實時進行擬合-微分-再微分，將在線數據的一階變化率和步驟3求得的一階變化率取值區間比較，識別出間歇過程的具體工段。將在線數據的二階變化率與步驟4得出的二階變化率取值區間比較，當參數超出取值區間時，則發出警報。

4 案例分析

4.1 工藝介紹

采用常見的間歇生產裝置——聚丙烯裝置的聚丙烯聚合過程作為研究對象，使用現場采集數據進行間歇過程早期異常情況識別。聚合釜是聚丙烯裝置中的重要部分，它使丙烯單體在催化劑、氫氣、活化劑和催化助劑的作用下自身發生加成聚合生成聚丙烯[14-15]。聚合釜反應過程中的主要工藝監測參數有聚合釜上溫、聚合釜中溫、聚合釜下溫和聚合釜壓力。聚合反應屬于劇烈反應，冷卻系統需保持良好水平，若溫度或壓力上升過快，可能引發爆炸。以聚合釜上溫為例進行說明。

4.2 趨勢分析報警監測

(1)分別選取歷史數據中連續10組樣本求取平均值，利用最小二乘法對數據進行多項式擬合，并對樣本進行工段劃分，圖1為3個階段中聚合釜上溫的擬合曲線圖，圖中的兩個采樣點之間隔有20個點。

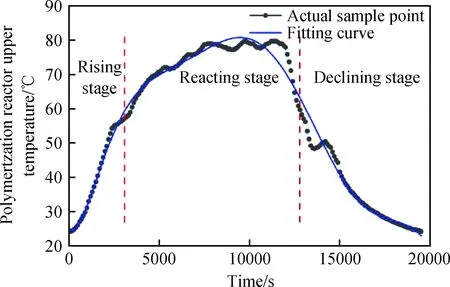
圖1 聚合釜上溫3個階段最小二乘擬合曲線Fig.1 The curve of the polymerization reactor temperature in three stages by least squares

(2)對歷史數據曲線進行一階微分計算，根據已經劃分的3個階段的參數取值，分別確定3個階段的一階變化率υ，如圖2所示。

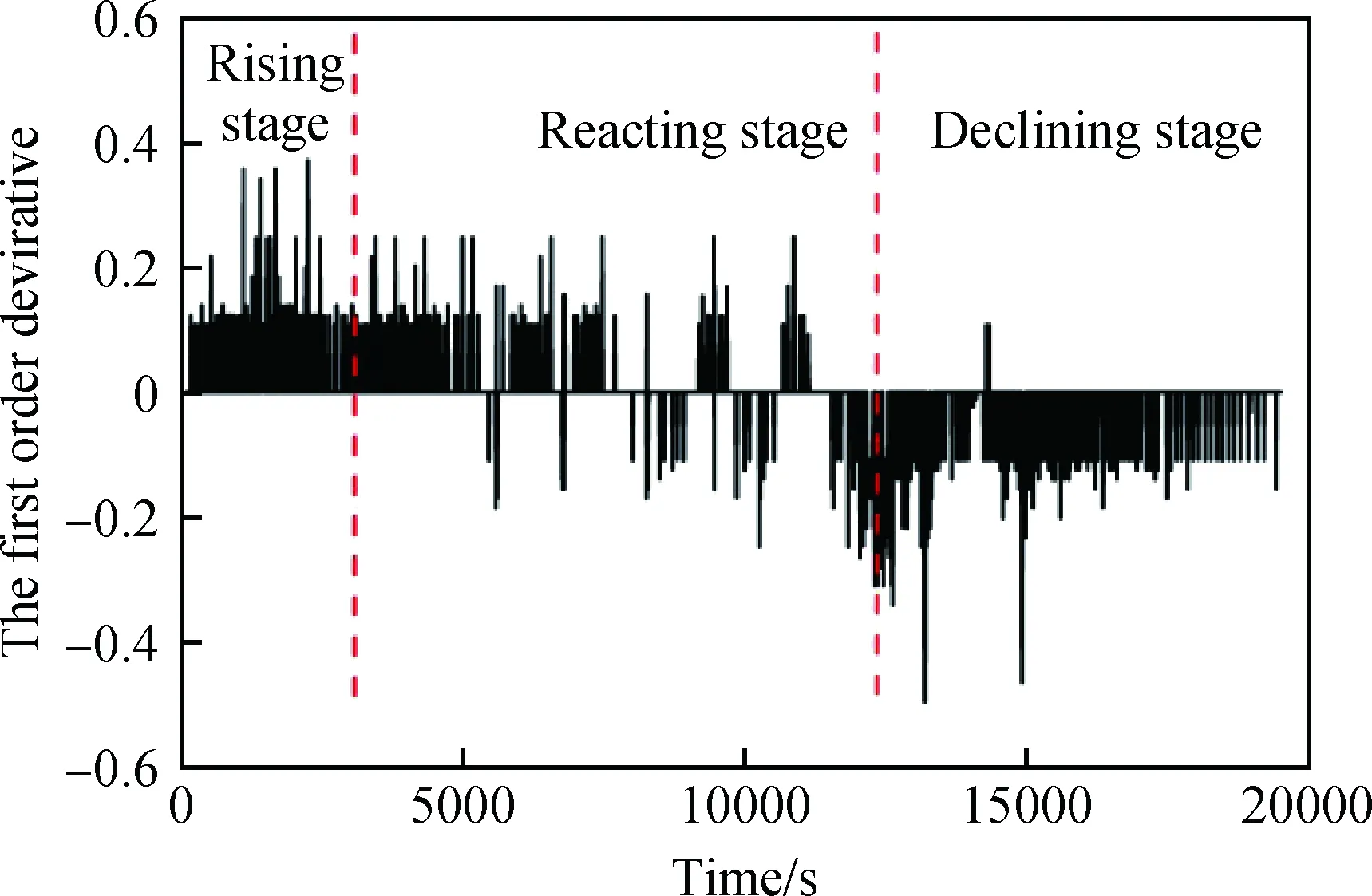
圖2 聚合釜上溫和一階變化率曲線Fig.2 The curve of the polymerization reactor temperature vs the first order derivative

根據圖1中的階段劃分和圖2中一階變化率的變化趨勢，確定一階變化率的取值區間，如表3所示。

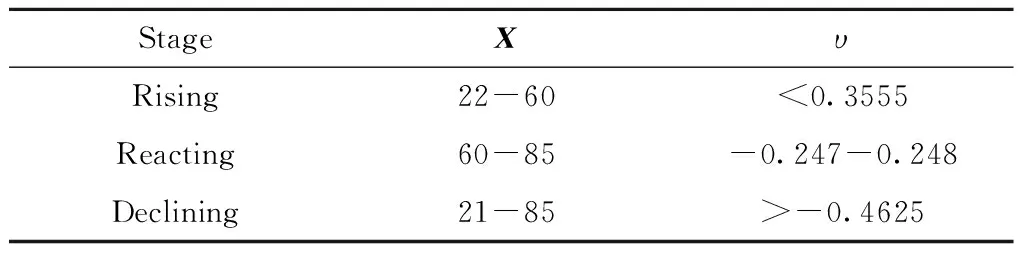
表3 聚合釜上溫和一階變化率取值區間Table 3 The range of values for polymerization reactor upper temperature and its first order derivative

(3)由于升溫過程較危險，因此選取聚合釜上溫的升溫階段重點進行監測。利用再微分方法計算參數二階變化率，并根據二階變化率的值將升溫階段劃分成穩定升溫階段和不穩定升溫階段，如圖3所示。通過二階變化率曲線趨勢，確定聚合釜上溫和二階變化率γ的取值區間，如表4所示。

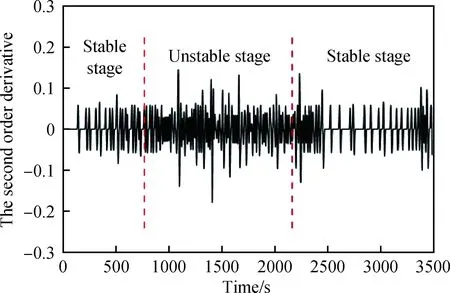
圖3 聚合釜上溫二階變化率曲線Fig.3 The curve of the polymerization reactor upper temperature vs the second order derivative

TrendXγStable22-29,56-60-0.07-0.07Unstable29-56-0.15-0.15

(4)由于升溫過程用時較短，滑動窗的長度也應較短。設置滑動窗長度為400 s，步長為5 s。選取一組聚合釜上溫升溫過快的異常數據，共511個采樣點(約42 min)，一般升溫過程持續50 min以上。前400 s的聚合釜上溫溫度及一階變化率曲線如圖4和圖5所示。由圖4、圖5可知，該段故障數據處于聚合過程中升溫階段。

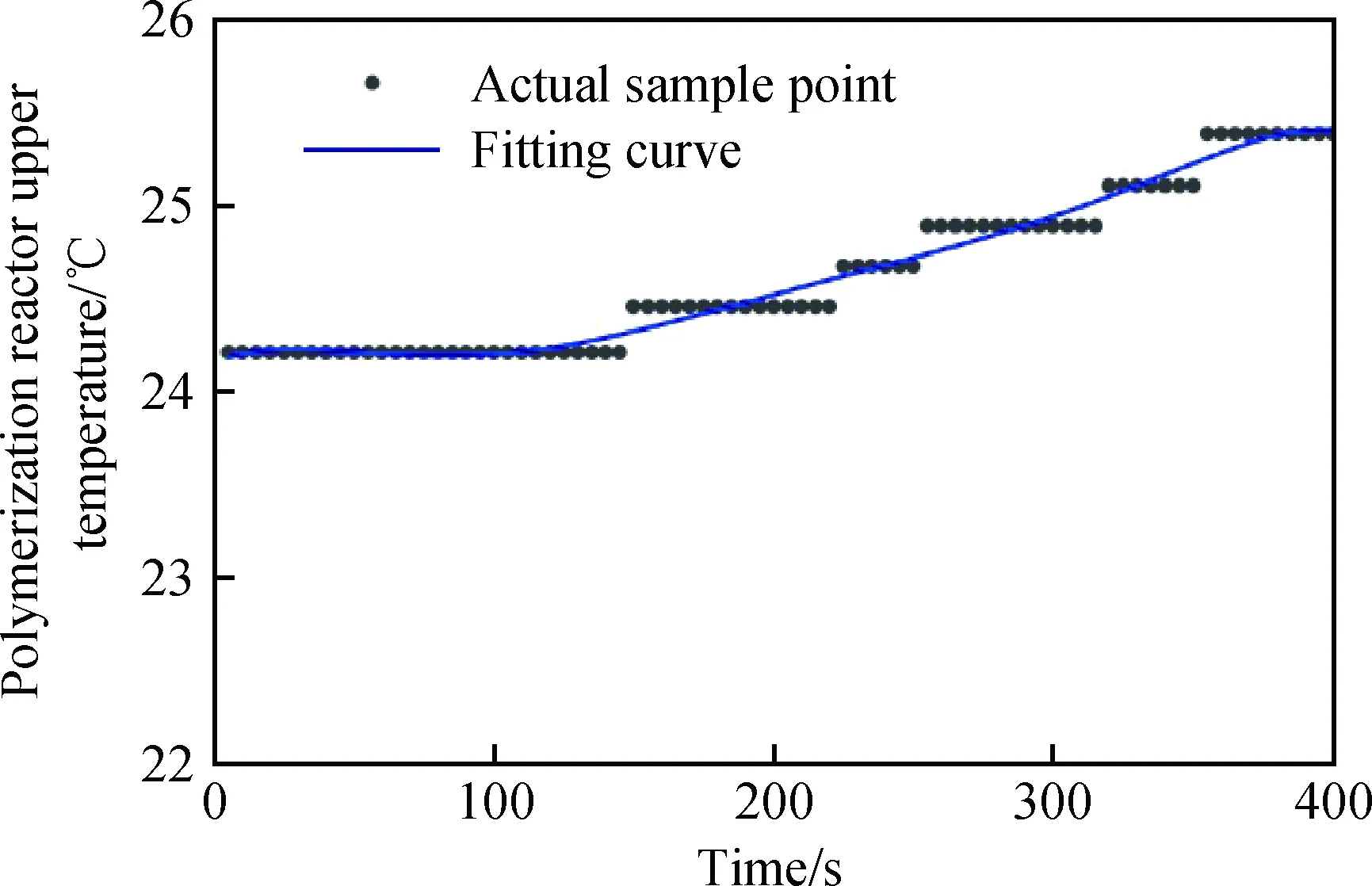
圖4 聚合釜上溫數據曲線Fig.4 The curve of the polymerization reactor upper temperature

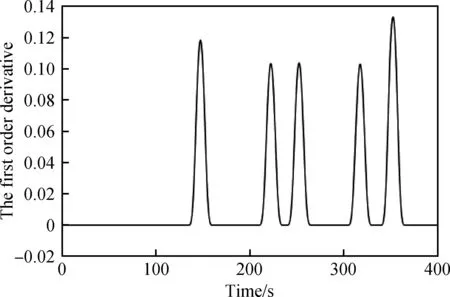
圖5 聚合釜上溫一階變化率曲線Fig.5 The curve of the polymerization reactor upper temperature vs the first order derivative

監測過程中，一階變化率曲線在第805 s時超出控制限，但瞬間恢復正常，此時的聚合釜上溫為32℃。之后在第1080 s，聚合釜上溫達到39℃時，對照表4，該時刻處于不穩定升溫階段，且開始連續超出報警限，如圖6所示。利用再微分得到該段數據的二階變化率曲線，如圖7所示。圖7中，在第1080 s二階變化率同樣超出報警線，說明在該采樣點處聚合釜上溫存在升溫速率過快的危險。

圖6 聚合釜上溫異常情況一階變化率曲線Fig.6 The curve of the polymerization reactor upper temperature abnormal situation vs the first order derivative

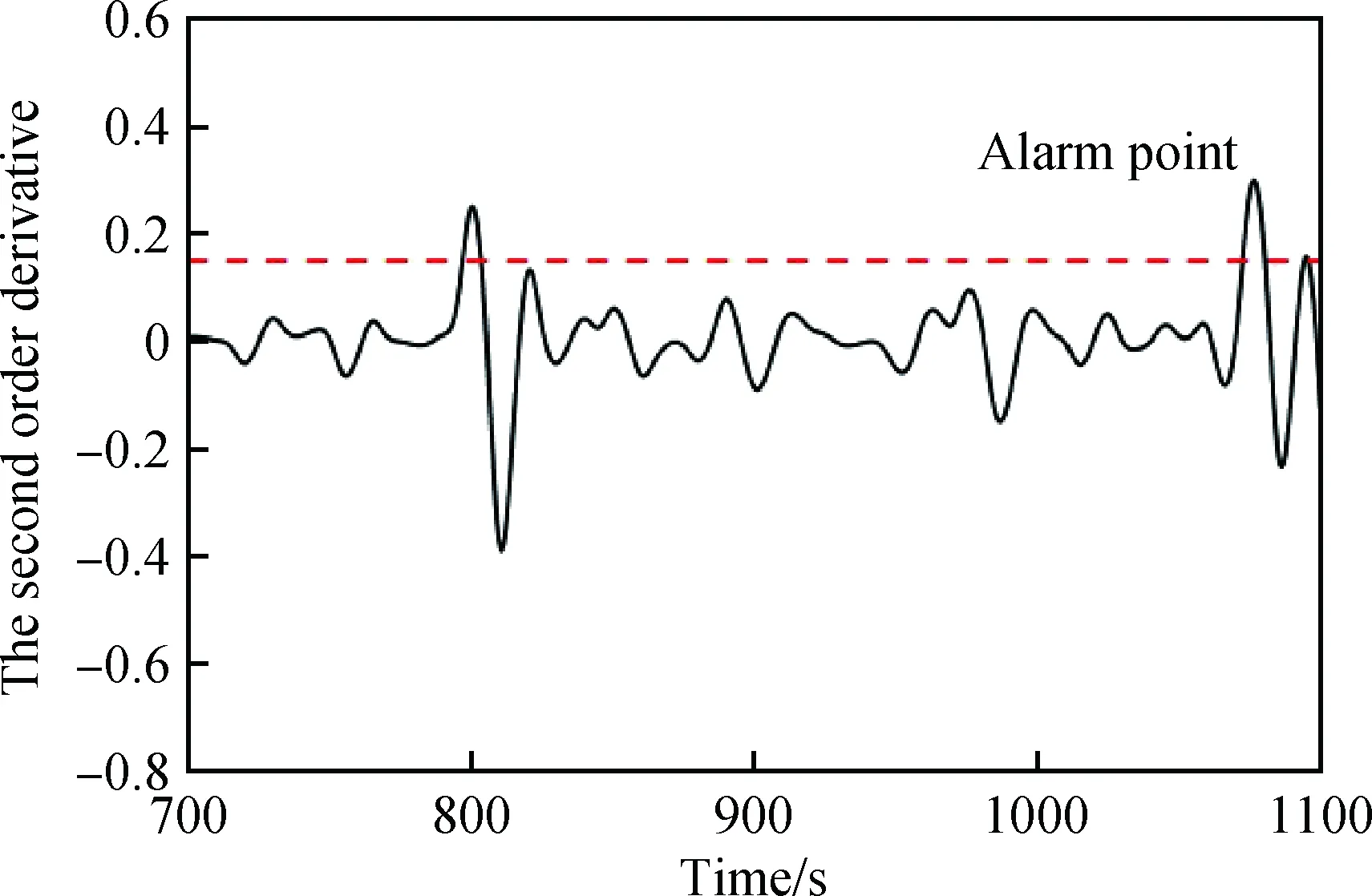
圖7 聚合釜上溫異常情況二階變化率曲線Fig.7 The curve of the polymerization reactor upper temperature abnormal situation vs the second order derivative

4.3 結果分析

(1)依據現場操作經驗，操作人員只能在聚合釜上溫升到60℃時才能發現發生升溫過快的異常情況。筆者所提出的趨勢分析方法能夠在第1080 s時監測出異常的發生，并及時發出報警，為現場操作提供了可靠的安全指導。

(2)為了驗證所提方法的有效性，采用3σ法與所提方法進行對比。根據聚合釜上溫升溫階段的10組歷史數據，由3σ法求得，聚合釜上溫服從均值為42.36，標準差為12.47的正態分布N(42.36，12.472)。利用3σ法對故障數據進行報警監測，采用[μ-2σ,μ+2σ]的報警閾值區間，但故障數據一直處于報警閾值內，在整個升溫階段都未能發現異常情況，如圖8所示。由3σ法和所提方法的比較可以得出，3σ法在聚合釜上溫出現升溫過快的早期無法監測出異常情況并報警，而所提趨勢分析方法在第1080 s時準確監測出異常的發生，提前24 min 34 s 發出報警。

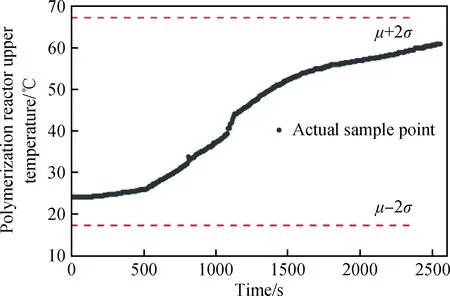
圖8 3σ法異常監測曲線Fig.8 The curve of the abnormal monitoring by the 3σ method

5 結 論

(1)針對現有的化工間歇過程報警研究沒有考慮在階躍變化過程中參數變化是否過快的問題，提出基于最小二乘的擬合-微分-再微分的趨勢分析方法，能夠準確識別間歇過程工況階段，重點監測間歇過程中的階躍變化階段，實現參數變化異常早期報警。

(2)采用最小二乘法對過程數據進行擬合，通過擬合-微分之后過程參數的變化趨勢進行間歇過程多時段工況識別，利用再微分對參數變化率的變化快慢分析，結合滑動窗算法，與報警閾值比較后，判斷參數變化是否異常。

(3)將所提方法應用于聚丙烯聚合過程，準確識別出故障數據處于聚合過程升溫階段，相比于3σ法，能夠提前24 min 34 s監測出異常情況的發生并發出報警。

符號說明：

a——擬合多項式系數；

D——滑動窗步長，s；

k——滑動窗更新次數；

L——滑動窗長度，s；

m——過程變量個數；

X——過程參數；

α——過程參數值；

β——參數一階變化率值；

ε——參數二階變化率值；

ν——參數一階變化率；

γ——參數二階變化率；

μ——正態分布均值；

σ——正態分布標準差。

[1] PENG Kaixiang, LI Qianqian, ZHANG Kai, et al. Quality-related process monitoring for dynamic non-Gaussian batch process with multi-phase using a new data-driven method[J].Neurocomputing, 2016,214: 317-328.

[2] 胡瑾秋， 張來斌， 王安琪. 基于格蘭杰因果關系檢驗的煉化系統故障根原因診斷方法[J].石油學報(石油加工), 2016, 32(6): 1266-1272.(HU Jinqiu, ZHANG Laibin, WANG Anqi. Fault root-cause diagnosis based on Granger causality test for petrochemical process system[J].Acta Petrolei Sinica(Petroleum Processing Section), 2016, 32(6): 1266-1272.)

[3] 馬曦， 張來斌， 胡瑾秋， 等. 基于IRML的油氣加工系統多層次故障傳播模型研究[J].石油學報(石油加工), 2015, 31(5): 1193-1202.(MA Xi, ZHANG Laibin, HU Jinqiu, et al. Hierachical fault propagation model for petroleum refining system based on IRML[J].Acta Petrolei Sinica(Petroleum Processing Section), 2015, 31(5): 1193-1202.)

[4] 蔡華偉. 聚合工藝重點參數的監控及安全控制[J].化工管理, 2014, (15): 186-188, 134.(CAI Huawei. Monitoring and safety control of key parameters in polymerization process[J].Chemical Management, 2014, (15):186-188, 134.)

[5] 郭小萍， 陸寧云， 高福榮， 等. 間歇過程滑動窗口子時段PCA建模和在線監測[J].控制與決策, 2005, 20(9): 1034-1037.(GUO Xiaoping, LU Ningyun, GAO Furong, et al. PCA modeling and on-line monitoring of sub-period of sliding window in batch process[J].Control and Decision, 2005, 20(9): 1034-1037.)

[6] 常玉清， 王姝， 譚帥， 等. 基于多時段MPCA模型的間歇過程監測方法研究[J].自動化學報, 2010, 36(9): 1312-1320.(CHANG Yuqing, WANG Shu, TAN Shuai, et al. Research on the monitoring method of batch process based on multi-period MPCA model[J]. Journal of Automation, 2010, 36(9): 1312-1320.)

[7] 王靜， 胡益， 侍洪波. 基于GMM的間歇過程故障檢測[J].自動化學報, 2015, 41(5): 899-905.(WANG Jing, HU Yi, SHI Hongbo. Fault detection based on GMM for batch processes[J].Journal of Automation, 2015, 41(5): 899-905.)

[8] 肖應旺， 徐保國. 基于ICA-MPCA的間歇過程監測方法[J].儀器儀表學報, 2009, 30(5): 990-996.(XIAO Yingwang, XU Baoguo. Monitoring method for batch process based on ICA-MPCA[J].Chinese Journal of Scientific Instrument, 2009, 30(5): 990-996.)

[9] 袁彬， 劉才學， 黃文樓， 等. 基于浮動報警閾值的燃料元件包殼破損監測方法的分析與研究[J].核動力工程, 2010, 31(1): 102-106.(YUAN Bin, LIU Caixue, HUANG Wenlou, et al. Analysis and research on fuel cladding failure monitoring based on floating alarm threshold[J].Nuclear Power Engineering, 2010, 31(1): 102-106.)

[10] 朱海， 高勝峰， 蔡鵬， 等. 基于拉依達準則的自適應小波閾值選取方法[J].海洋技術學報, 2016, 35(4): 50-54.(ZHU Hai, GAO Shengfeng, CAI Peng, et al. Study on the self-adaptive wavelet threshold selection method based on the Pauta criterion[J].Journal of Ocean Technology, 2016, 35(4): 50-54.)

[11] 田垅， 劉宗田. 最小二乘法分段直線擬合[J].計算機科學, 2012, 39(S1): 482-484.(TIAN Long, LIU Zongtian. Least-square method of piecewise linear fitting[J] .Computer Science, 2012, 39(S1): 482-484.)

[12] MARCO A, MARTNEZ J J.Polynomial least squarefitting in the Bernstein basis[J].Linear Algebra and Its Applications, 2010, 433(7): 1254-1264.

[13] 陳桂秀. 用程序求解最小二乘擬合多項式的系數[J].青海師范大學學報(自然科學版), 2010, 26(3): 14-17.(CHEN Guixiu. Solve the least square curve fitting polynomial coefficient with program[J].Journal of Qinghai Normal University (Natural Science), 2010, 26(3): 14-17.)

[14] 蔡華偉. 聚合工藝重點參數的監控及安全控制[J].化工管理, 2014, (15): 186-188, 134.(CAI Huawei. Monitoring and safety control of key parameters in polymerization process[J].Chemical Management, 2014, (15): 186-188, 134.)

[15] 林觀炎， 喬建江， 吳達嶺. 聚丙烯生產工藝危險性分析及安全措施[J].安防科技, 2012, (1): 24-27.(LIN Guanyan, QIAO Jianjiang, WU Daling. Hazard analysis and safety measures of polypropylene production process[J].Safety and Environmental Engineering, 2012, (1): 24-27.)