噴霧造粒塔內流動不穩定性的實驗研究
馮留海, 卜億峰, 孫中衛, 趙 凡, 毛 羽, 門卓武
(1.北京低碳清潔能源研究所, 北京 102209; 2.中國石油大學 重質油國家重點實驗室, 北京 102249; 3.新奧科技發展有限公司, 河北 廊坊 065001; 4.蘭州蘭石能源裝備工程研究院有限公司, 甘肅 蘭州 730314)
以超臨界烷烴為抽提溶劑進行重質油梯度分離是近年提出的重質油加工新工藝[1],具有很好的應用前景。超臨界溶劑可以選擇性去除渣油中的瀝青質,從而得到加工性能較好的脫瀝青油和高軟化點的脫油瀝青,而脫油瀝青在噴霧造粒塔內可實現瀝青造粒和溶劑分離回收[2],所以有必要研究噴霧造粒塔內的流動特性。
為實現氣-固兩相的高效分離,早期學者主要從宏觀角度分析結構參數[3]和操作參數[4]對設備分離性能的影響規律。隨著研究的深入,單純對設備內時均流動特性進行研究已無法滿足要求,因此很多學者開始研究瞬時流動特性[5]。對旋風分離器和造粒塔等旋流分離設備的研究發現,設備內除了整體的螺旋旋轉流動外,還存在各種不穩定的擺動,呈現出一定的流動不穩定性,這會對分離性能、壓降損失等產生不利影響。Gupta等[6]實驗測量了噴嘴的流動過程,發現強旋流使得強制渦變得不穩定,形成隨時間變化的旋進渦核,并且觀察到幾何結構對稱的設備內也會出現不穩定流動。王甜等[7]采用熱膜測速系統測量了旋風分離器內的瞬時速度場,并討論了旋流擺動對切向速度的影響。Gao等[8]采用壓力傳感器測量了旋風分離器內軸向壓力脈動,并根據頻率變化確定了自然旋風長尾渦位置。隨著測量技術的發展,采用非接觸式技術具有更高的時間和空間分辨率。Nikiforaki等[9]和Galletti等[10]采用頻譜分析方法實驗研究了攪拌器的宏觀不穩定性流動,發現雷諾數(Re)對宏觀流動不穩定性影響較大。近年來,采用實驗和數值模擬相結合的方法多角度研究設備內的流動特性成為研究的趨勢。Derksen等[11-12]和吳小林等[13-14]使用數值模擬得到的旋風分離器內速度分布和旋進渦核擺動的峰值頻率與實驗結果吻合較好。Lebarbier等[15-16]利用實驗和數值模擬研究了不同旋流數下軸流噴霧干燥器內的流動特性,采用快速傅里葉變換技術(Fast Fourier Transformation, FFT)研究了速度主頻,考察了葉片角度對流動穩定性的影響。雖然前人對設備內流場擺動特性進行了研究,但是大多局限在單點研究,并未對全部流場進行系統分析。噴霧造粒塔內為稀相氣-固兩相流動過程(瀝青相固含率小于1%),且絮狀顆粒的堆積密度較低(堆積密度大概為120 kg/m3),說明固體顆粒具有較好的跟隨性,所以本研究重點在于噴霧造粒塔內的單相流動過程。筆者擬采用激光多普勒測速儀(PDPA)測量噴霧造粒塔內單相空氣的瞬時速度分布,再根據傅里葉變換處理瞬時速度獲得設備內的頻率分布和擺動特性,以期提高對噴霧造粒塔內瞬時流動規律的認識。
1 噴霧造粒塔速度場實驗裝置和測量方法
噴霧造粒塔速度場實驗測量流程如圖1所示。壓縮機向穩壓罐內注入壓縮空氣,通過轉子流量計后進入發煙器內,與示蹤粒子均勻混合后,以一定角度和速度從陣列噴嘴射入噴霧造粒塔內。流體介質在噴霧造粒塔外側形成向下的射流旋轉流場,在底部壁面的約束下反轉上行并從頂部排氣管排出。實驗時,壓力表測量穩壓罐及噴嘴入口壓力,浮子流量計測量氣體風量。
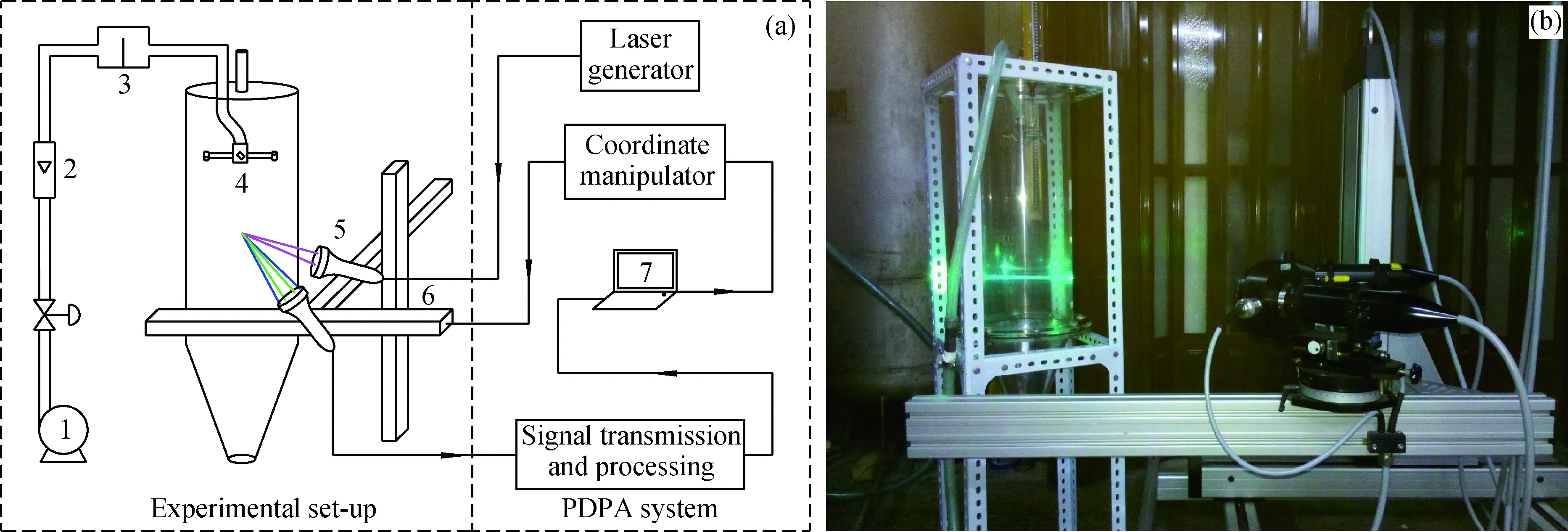
圖1 噴霧造粒塔流場測量流程圖和裝置照片Fig.1 Schematic and picture of experiment set-up for measurement of flow field in a spray granulation tower (a) Schematic of experiment set-up; (b) Picture of test equipment 1—Compressor; 2—Rotameter; 3—Tracer particle generator; 4—Spray granulation tower; 5—Laser emitter/detector; 6—3D traverse system; 7—Computer
噴霧造粒塔結構及測量位置分布如圖2所示,筒體高度和內徑分別為500 mm和200 mm,筒體下端與高度為208 mm的錐體相連,錐體底部密封。噴霧造粒塔的核心部件是距離頂蓋下方90 mm處的陣列噴嘴,4個內徑d=4 mm的噴嘴均布在直徑為96 mm的圓周上。實驗過程中可以通過旋轉噴嘴來控制射流方向,選擇的噴嘴角度α=45°。設陣列噴嘴所在平面為水平面(z=0 mm),沿軸向向下布置5個測量位置,各測量位置沿徑向到壁面等間距布置33個測點,即相鄰兩測點間距為3 mm。PDPA理論上不需要進行校正,并具有很好的測量精度[17]。王江云等[18]驗證了衛生香具有較好的跟隨性,所以在本研究中也選擇衛生香作為示蹤粒子。測量時每個測點取5000個樣本,且保證數據有效性在70%以上。
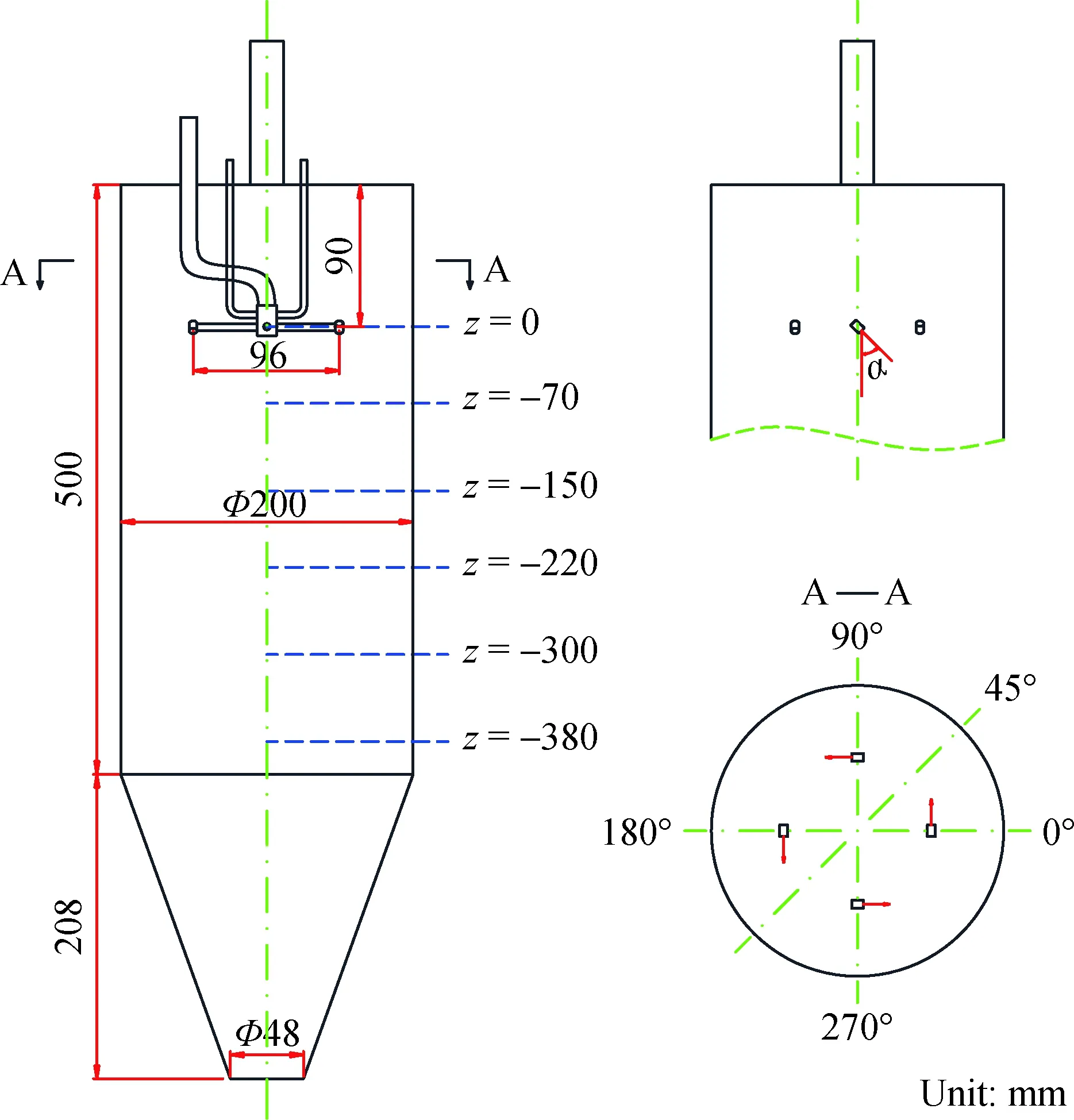
圖2 噴霧造粒塔示意圖和測量點布置Fig.2 Physical model and the location of measurement points for a spray granulation tower
PDPA記錄的是測點的瞬時速度,對其進行相應的處理,可以得到各測點的統計結果。對測點的數據進行加和平均可以得到平均值,其公式見式(1)。
(1)
同時,還可以根據速度場求得均方根和湍流度,其公式見式(2)和式(3)。
(2)
(3)
2 結果與討論
前人通過噴霧造粒塔內時均速度分布發現流場存在明顯的分區特性[19],上部區域流動復雜、規律性較差,所以筆者重點分析下部流動規律性較好區域的瞬時不穩定流動過程。
2.1 噴霧造粒塔內瞬時速度分布
圖3為入口流量Q=6.0 m3/h時z=-300 mm截面沿徑向瞬時切向速度波動變化規律。從圖3可以看出,瞬時速度在時均速度附近波動,不同位置處瞬時切向速度波動都比較大,說明噴霧造粒塔內的氣相流動處于高度脈動變化狀態。中心區瞬時切向速度的波動范圍約為1.5 m/s,而外側區域的波動范圍約為1.0 m/s。
圖4為入口流量Q=6.0 m3/h時z=-300 mm截面沿徑向瞬時軸向速度波動變化規律。從圖4可以看出,瞬時軸向速度與瞬時切向速度波動規律類似,都隨時間作較大的振蕩波動,進一步說明了噴霧造粒塔內氣相流動為高度湍動變化狀態,且各位置的波動范圍約為1.0 m/s。
2.2 噴霧造粒塔內均方根和湍流度分布
圖5為不同入口流量下各縱截面的切向均方根和切向湍流度分布趨勢。從圖5(a)可以看出,切向均方根數值在壁面附近比較大,這是由于流體受壁面的阻礙作用導致在壁面附近速度變化比較劇烈,說明壁面附近存在較大的速度梯度,產生了較強的湍流。因為噴霧造粒塔內為弱旋流動,速度的脈動變化不是很劇烈,從而導致其他區域的切向均方根數值都比較小,所以切向湍流度能更直觀地描述流場的湍流狀態。從圖5(b)可以看出,切向湍流度在不同位置的分布趨勢基本相似,沿徑向都呈先減小后增加的“W”型分布趨勢。由于中心區流體擺動使得流動比較紊亂,導致切向湍流度較大,而湍流度的強弱表明擺動的劇烈程度。由于壁面附近的切向均方根較大,而平均切向速度值較小,所以切向湍流度在壁面附近較高。對比不同入口流量下的切向均方根和切向湍流度發現,其分布規律基本一致,且量值上也基本相同,說明流量的改變對分布趨勢的影響較小。
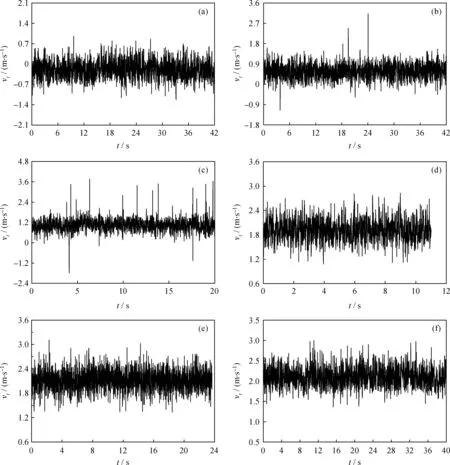
圖3 不同徑向位置瞬時切向速度(vt)隨時間的波動關系Fig.3 Variation of instantaneous tangential velocity (vt) along with time in different radial positions Q=6.0 m3/h; z=-300 mm r/R: (a) 0; (b) 0.2; (c) 0.3; (d) 0.5; (e) 0.6; (f) 0.8
圖6為不同入口流量下各縱截面的軸向均方根和軸向湍流度分布趨勢。從圖6(a)可以看出,軸向均方根的分布趨勢比較平緩,僅在壁面附近有較明顯的波動,說明在壁面附近存在較大的速度梯度,與切向均方根結果相印證,但是整體而言各處的波動并無明顯變化。從圖6(b)可以看出,軸向湍流度的變化非常復雜,這是由于在中心區和壁面附近軸向速度較小,且噴霧造粒塔內的上、下行流流動過程使得分界面附近的軸向速度較小,從而導致軸向湍流度在上、下行流的分界面附近變化明顯。
2.3 噴霧造粒塔內流動不穩定性分析
借助Matlab軟件編譯傅里葉變換算法,可以獲得不同位置瞬時速度信號對應的頻率和幅值等信息。圖7為瞬時切向速度變換得到的頻譜圖。從圖7可以看出,每個測點位置都存在一個明顯的主頻,除此之外也有許多次頻和幅值很低的高頻。由主頻可以看出,噴霧造粒塔內存在較穩定的周期性擺動;存在多個次頻說明流場是由多個頻率的速度波動疊加組成的混合流動過程;幅值很低的高頻信號反映了湍流的隨機特征。從頻譜圖可以看出噴霧造粒塔內流動的復雜性。由于脈動速度反映了氣相的湍流變化,具有一定的隨機性,且是無規則的高頻振蕩,所以理應存在的是連續波譜,而不應該存在一個集中分布的頻率。因此這個集中分布的頻率是噴霧造粒塔內大尺度擺動引起的。
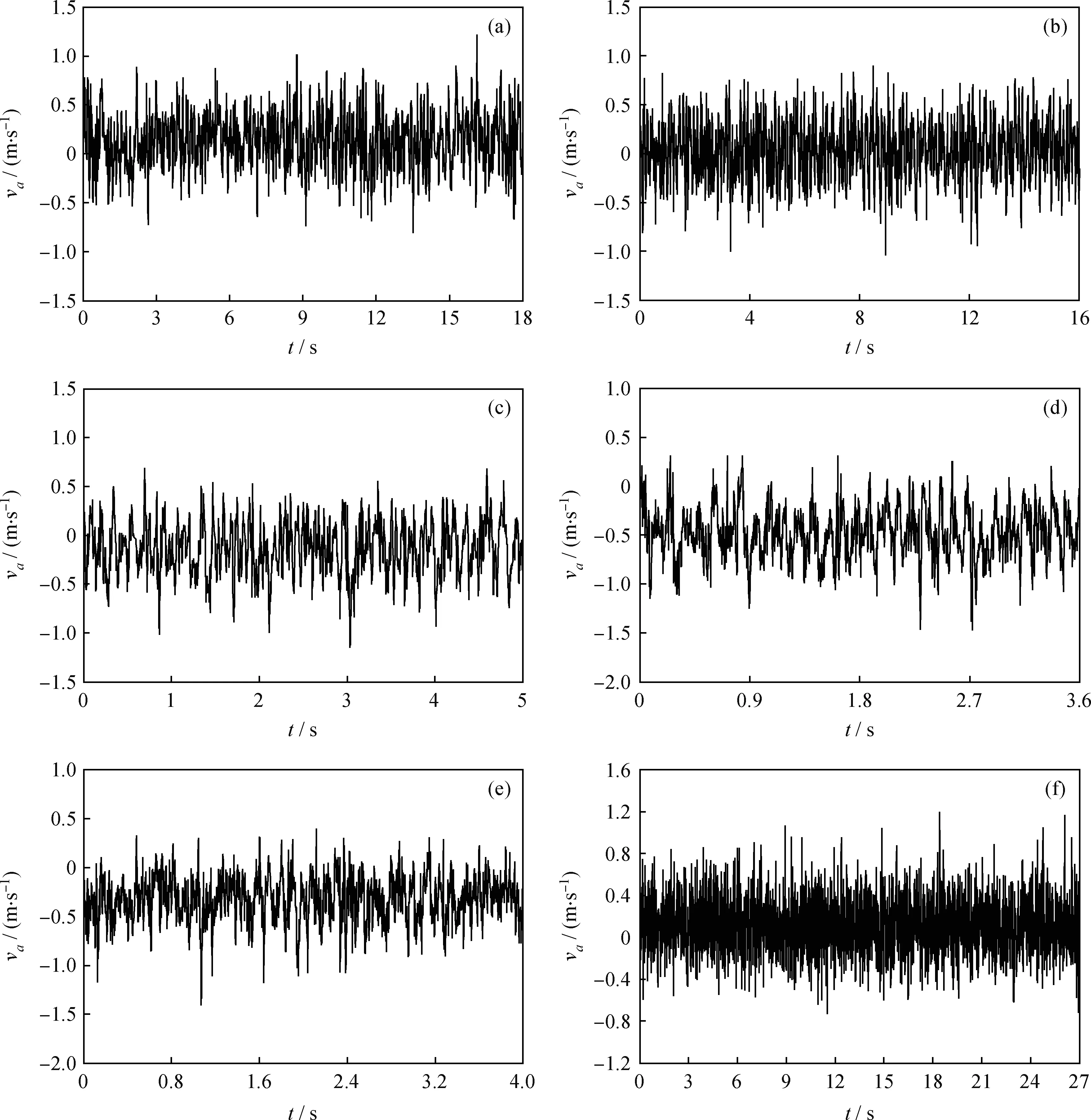
圖4 不同徑向位置瞬時軸向速度(va)隨時間的波動關系Fig.4 Variation of instantaneous axial velocity (va) along with time in different radial positions Q=6.0 m3/h; z=-300 mm r/R: (a) 0; (b) 0.2; (c) 0.3; (d) 0.5; (e) 0.6; (f) 0.8
圖8為z=-300 mm截面瞬時速度對應的頻率沿徑向分布。從圖8可以看出,各測點瞬時切向速度和軸向速度經傅里葉變換得到的主頻基本一致。以r/R=0.2為界存在兩組不同頻率的擺動,其中中心區主頻大概為7.6 Hz,外側區域主頻大概為8.6 Hz。由于中心切向速度較小,中心下行流受環形上行流的黏性力剪切作用較低,從而使得內部旋流速度滯后于外側旋流,最終導致噴霧造粒塔內出現兩個主頻,對比發現,頻率與上、下行流分界面吻合較好[5]。

圖5 不同流量下縱截面切向均方根(σt)和 切向湍流度(δt)分布Fig.5 Profiles of tangential RMS (σt) and tangential turbulence intensity (δt) under different flow Q1=6.0 m3/h; Q2=3.0 m3/h (a) Tangential RMS (σt); (b) Tangential turbulence intensity (δt)
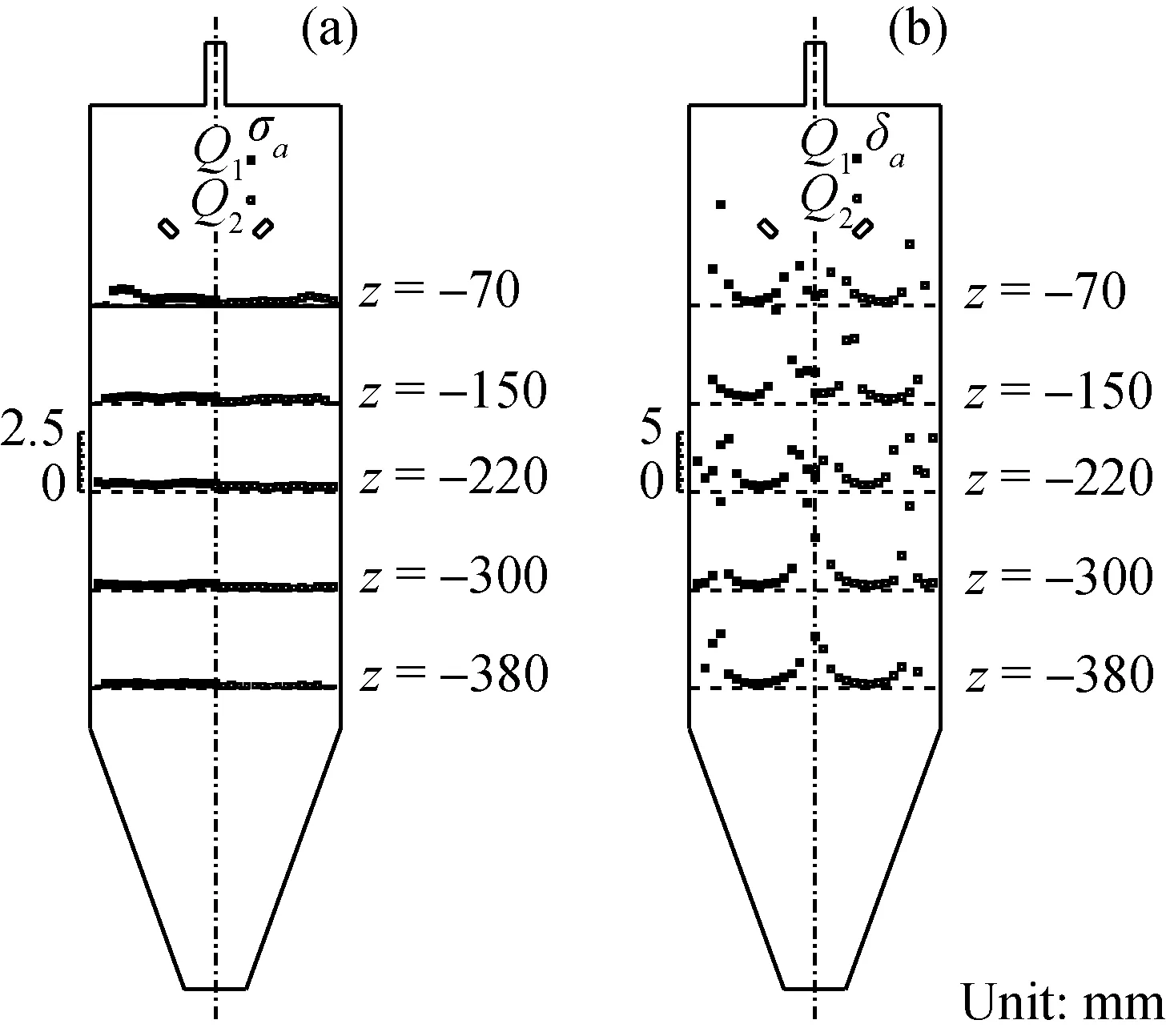
圖6 不同流量下縱截面軸向均方根(σa)和 軸向湍流度(δa)分布Fig.6 Profiles of axial RMS (σa) and axial turbulence intensity (δa) under different flow Q1=6.0 m3/h; Q2=3.0 m3/h (a) Axial RMS (σa); (b) Axial turbulence intensity (δa)

圖7 不同徑向位置瞬時切向速度頻譜圖Fig.7 Spectrum of instantaneous tangential velocity in different radial positions Q=6.0 m3/h; z=-300 mm r/R: (a) 0; (b) 0.2; (c) 0.3; (d) 0.5; (e) 0.6; (f) 0.8
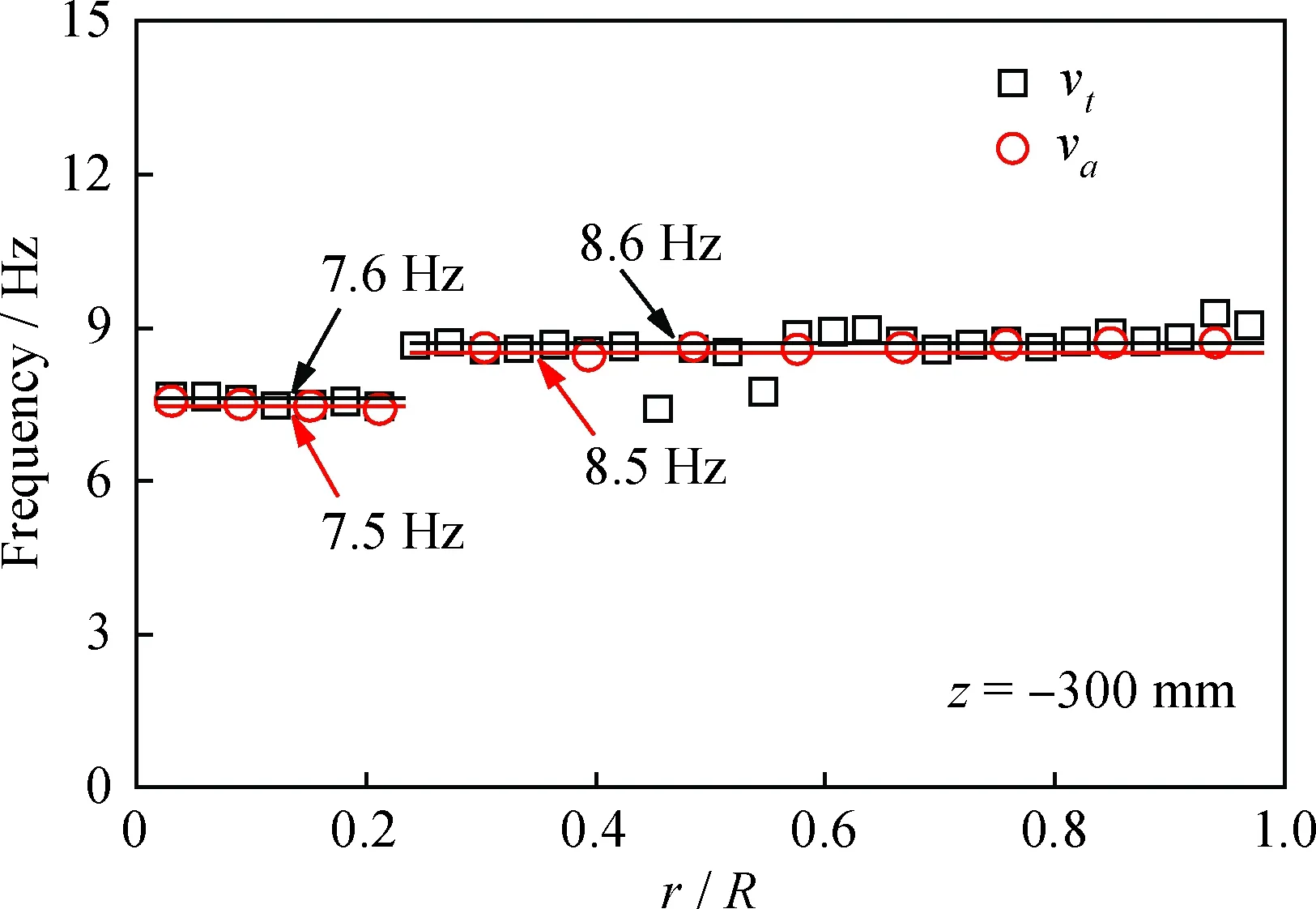
圖8 不同徑向位置瞬時切向和軸向速度對應的頻率分布Fig.8 Frequency of instantaneous tangential and axial velocity in different radial positions Q=6.0 m3/h; z=-300 mm
3 結 論
(1)非接觸式測量技術具有更高的時空分辨率,具有更好的解析復雜流場的流動特性。噴霧造粒塔內瞬時速度隨時間波動較大,體現了射流旋轉流場流動不穩定。噴霧造粒塔內切向和軸向湍流度在邊壁附近強度高于中心區域,說明邊壁附近瞬時速度的湍流脈動強烈。
(2)瞬時速度頻譜圖基本都是由一個明顯主頻、多個次頻和低幅高頻組成,說明設備內流場是由一個較強擺動、多個波動和湍流脈動疊加的流場,反映了噴霧造粒塔內流動的復雜性。
(3)對于流場內確定的點,其瞬時切向和軸向速度所對應的主頻基本相同,并且由于黏性切應力的作用使得內部旋流速度滯后于外側旋流速度,從而造成以r/R=0.2為界,中心區主頻低于外側區域。
符號說明:
N——測量采樣數;
Q——入口流量,m3/h;
r——沿半徑方向的位置,mm;
R——筒體的半徑,mm;
t——時間,s;
vi——瞬時速度,m/s;


x、y、z——笛卡爾坐標系,mm;
Ф——直徑,mm;
α——噴射角度,°;
δ——湍流度;
σ——速度均方根,m/s;
下標
a——軸向;
i——i方向;
t——切向。
[1] 徐春明, 趙鎖奇, 盧春喜, 等. 重質油梯級分離新工藝的工程基礎研究[J].化工學報, 2010, 61(9): 2393-2400. (XU Chunming, ZHAO Suoqi, LU Chunxi, et al. Engineering basics of heavy oil deep stage separating process[J].Journal of Chemical Engineering of Chinese Universities, 2010, 61(9): 2393-2400.)
[2] 孫顯峰, 孫學文, 趙鎖奇, 等. PGSS法用于脫油瀝青顆粒的制備[J].化工學報, 2010, 24(2): 290-296. (SUN Xianfeng, SUN Xuewen, ZHAO Suoqi, et al. Preparation of de-oiled asphalt particles by PGSS process[J].Journal of Chemical Engineering of Chinese Universities, 2010, 24(2): 290-296.)
[3] 王娟, 毛羽, 孫曉偉, 等. 陣列旋轉式射流分布器的結構設計與實驗研究[J].化工學報, 2011, 62(2): 393-398. (WANG Juan, MAO Yu, SUN Xiaowei, et al. Design and experimental study of arraying and revolving jet flow distributor[J].Journal of Chemical Industry and Engineering, 2011, 62(2): 393-398.)
[4] LIU M, YU M, WANG J, et al. Effect of swirl on hydrodynamics and separation performance of a spray granulation tower with array nozzles[J].Powder Technology, 2012, 227(9): 61-66.
[5] FENG L, LIU M, WANG J, et al. Study on the flow instability of a spray granulation tower[J].Separation & Purification Technology, 2016, 169: 210-222.
[6] GUPTA A K, LILLEY D G, SYRED N. Swirl Flows[M].Tunbridge wells: Abacus Press, 1984.
[7] 王甜, 徐俊, 宋健斐, 等. 旋風分離器內旋轉流的不穩定性[J].化工學報, 2010, 61(2): 317-322. (WANG Tian, XU Jun, SONG Jianfei, et al. Instability of swirling flow in a cyclone separator[J].Journal of Chemical Industry and Engineering, 2010, 61(2): 317-322.)
[8] GAO C, SUN G, DONG R, et al. Characterizing the dynamic property of the vortex tail in a gas cyclone by wall pressure measurements[J].Fuel Processing Technology, 2010, 91(8): 921-926.
[9] NIKIFORAKI L, MONTANTE G, LEE K C, et al. On the origin, frequency and magnitude of macro-instabilities of the flows in stirred vessels[J].Chemical Engineering Science, 2003, 58(13): 2937-2949.
[10] GALLETTI C, PAGLIANTI A, LEE K C, et al. Reynolds number and impeller diameter effects on instabilities in stirred vessels[J].AIChE Journal, 2004, 50(9): 2050-2063.
[11] DERKSEN J J, VAN D A H E A. Simulation of vortex core precession in a reverse-flow cyclone[J].AIChE Journal, 2000, 46(7): 1317-1331.
[12] DERKSEN J J. Simulations of confined turbulent vortex flow[J].Computers & Fluids, 2004, 34(3): 301-318.
[13] 吳小林, 嚴超宇, 時銘顯. 雙入口直切式旋風分離器流場內旋進渦核現象的研究[J].化工機械, 2002, 29(1): 1-4. (WU Xiaolin, YAN Chaoyu, SHI Mingxian. Study on the phenomenon of swirling vortex in the flow field of a double inlet straight cut cyclone separator[J].Chemical Machinery, 2002, 29(1): 1-4.)
[14] 吳小林, 熊至宜, 姬忠禮, 等. 旋風分離器旋進渦核的數值模擬[J].化工學報, 2007, 58(2): 383-390. (WU Xiaolin, XIONG Zhiyi, JI Zhongli, et al. Numerical simulation of vortex core in cyclone separator[J].Journal of Chemical Industry and Engineering, 2007, 58(2): 383-390.)
[15] LEBARBIER C, KOCKEL T K, FLETCHER D F, et al. Experimental measurement and numerical simulation of the effect of swirl on flow stability in spray dryers[J].Chemical Engineering Research & Design, 2001, 79(3): 260-268.
[16] LANGRISH T A G, WILLIAMS J, FLETCHER D F. Simulation of the effects of inlet swirl on gas flow patterns in a pilot-scale spray dryer[J].Chemical Engineering Research & Design, 2004, 82(7): 821-833.
[17] LIU Y, YANG Q, QIAN P, et al. Experimental study of circulation flow in a light dispersion hydrocyclone[J].Separation and Purification Technology, 2014, 137(24): 66-73.
[18] 王江云, 毛羽, 孟文, 等. 旋風分離器內非軸對稱旋轉流場的測量[J].石油學報(石油加工),2015, 31(4): 920-929. (WANG Jiangyun, MAO Yu, MENG Wen, et al. Experimental measurement of non-axisymmetric rotating flow field in cyclone separator[J].Acta Petrolei Sinica (Petroleum Processing Section), 2015, 31(4): 920-929.)
[19] 馮留海, 趙凡, 劉美麗,等. 噴嘴徑向位置對噴霧造粒塔流動特性的影響[J].石油學報(石油加工), 2016, 32(5): 1013-1019. (FENG Liuhai, ZHAO Fan, LIU Meili, et al. Effect of nozzle position on the flow behavior in a spray tower[J].Acta Petrolei Sinica (Petroleum Processing Section), 2016, 32(5): 1013-1019.)

