基于M-QSPR的乙醇-汽油參比燃料混合物辛烷值的理論預測

張彭非， 潘 勇， 管 進， 蔣軍成

(南京工業大學 安全科學與工程學院， 江蘇 南京 210009)

近年來，乙醇汽油的使用量快速增長。美國能源獨立和安全法案強制要求，美國可再生能源的使用量要從2007年的90億加侖(1美制加侖約3.79升)上升到2020年的360億加侖[1]。發動機爆震現象是由火焰前鋒未燃燒的燃料與空氣混合物的自燃引起的[2-3]，是制約火花發動機達到更高熱效率的一個重要因素，這種自燃現象產生的壓力波會對發動機硬件造成嚴重損壞[4]。辛烷值是衡量包括乙醇汽油在內的汽油產品抗爆性能的重要參數，辛烷值越高，抗爆震性越強。因此，研究乙醇汽油的辛烷值，對其安全使用和儲存具有重要意義。

通過實驗測定是目前獲取汽油辛烷值數據的最有效方法。根據ASTM D2699[5]和ASTM D2700[6]的規定，辛烷值分為研究法辛烷值(RON)和馬達法辛烷值(MON)兩種。通過實驗測定來改善調試汽油樣品的辛烷值從而確定其最佳配比，不僅需要昂貴的實驗儀器及設備，還需要花費大量的時間及試劑樣品[7]。因此，有必要開展汽油辛烷值的理論預測研究，建立可靠的理論預測模型，彌補實驗方法的缺陷與不足。

目前，分析化學法是文獻上預測汽油辛烷值的常見方法。Ghosh等[8]、Lugo等[9]和Albahri等[10]通過色譜分析法來預測汽油辛烷值，平均誤差值約為4～7。Kardamakis等[11]、王宗明等[12]、史月華等[13]則通過近紅外光譜法對汽油辛烷值進行預測研究。分析化學法的缺陷在于同樣需要用到相應分析測試儀器，其運轉、維護費用較高，且耗時耗力。因此，采用各種理論算法來建立汽油辛烷值的預測模型受到廣泛關注。

定量結構-性質相關性(Quantitative structure-property relationship, QSPR)研究是一種根據分子結構有效預測有機物理化性質的理論方法。目前，相關研究者已應用該方法對單一汽油組分的辛烷值進行了預測研究[14-17]。然而，文獻中針對含乙醇汽油混合體系的混合物定量結構-性質相關性(M-QSPR)的研究鮮見。

在本研究中，從分子結構角度出發，以乙醇-汽油參比燃料混合物為研究對象，針對其研究法辛烷值開展混合體系的M-QSPR研究，建立相應的理論預測模型，揭示相應的特征結構因素及其影響規律，為工程上提供一種根據分子結構快速預測乙醇-汽油參比燃料混合物辛烷值的新方法。

1 實驗部分

1.1 實驗樣本及樣本集劃分

乙醇在改善發動機爆震現象方面作用明顯[18-20]。與傳統汽油相比，乙醇汽油具有明顯更高的辛烷值。按照我國的國家標準，乙醇汽油是用普通汽油與燃料乙醇調和而成。在目前國內外相關研究中，通常以正參比燃料(異辛烷與正庚烷的混合物)作為汽油產品的替代燃料來測定或研究汽油的辛烷值。在此基礎上，筆者對實際乙醇汽油體系進行簡化，針對乙醇與汽油參比燃料的混合物(即乙醇-異辛烷-正庚烷三元混合物)開展相關研究。

在本研究中所使用的乙醇-汽油參比燃料混合物實驗樣本集均來源于文獻[21]，總計有44個研究法辛烷值(RON)樣本。其中80%的樣本劃分為訓練集(序號1-35)，用于建立預測模型；20%的樣本劃分為測試集(序號36-44)，用于模型的外部驗證。詳細樣本數據見表1[21]。

1.2 混合描述符的計算

在本研究中應用分子結構的簡單表征(Simplex representation of molecular structure, SiRMS)描述符對乙醇-汽油參比燃料混合物的分子結構特征進行表征。SiRMS描述符是一種分子結構參數描述符[22-23]，它通過對分子進行四原子碎片化實現混合體系分子結構特征的表征。SiRMS描述符不僅可以表征分子的原子類型、鍵型，還能表征原子之間的拓撲結構等信息。SiRMS描述符總計有11種拓撲結構類型，具體見表2。SiRMS描述符的計算公式如式(1)：

D=x1D1+x2D2+x3D3

(1)

式中，x1、x2、x3為各組分的摩爾系數；D1、D2、D3為各組分中某個四原子碎片的數量。

根據表2的結構劃分方式可知，本研究中使用樣本中涉及的SiRMS描述符共計25個。

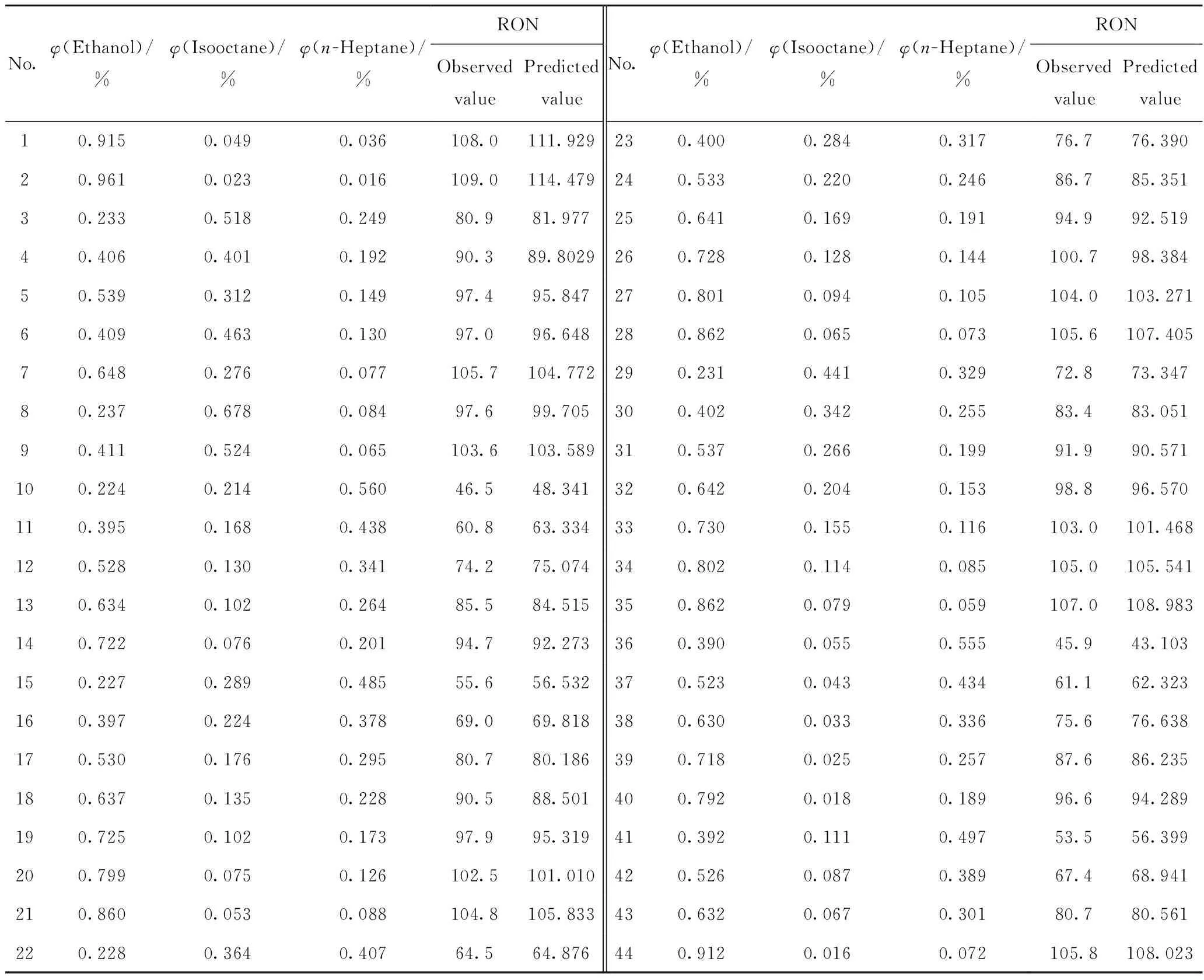
表1 乙醇-汽油參比燃料混合物各組分比例及其RON值[21]Table 1 Compositions and the RON values of ethanol-primary reference fuel mixtures[21]

表2 四原子碎片拓撲結構類型Table 2 Topological structure types of tetratomic fragments

1.3 描述符的篩選及建模

在本研究中應用遺傳-多元線性回歸(GA-MLR)組合算法對上述SiRMS描述符進行優化篩選與建模，建立最優的乙醇-汽油參比燃料混合物辛烷值線性預測模型。GA-MLR算法結合了遺傳算法GA的全局優化搜索能力[24]和多元線性回歸MLR簡便直觀的建模能力，具有較好的變量選擇和模型優化效果。GA-MLR算法通過MATLAB軟件編寫，相關參數設置為：群體中個體的數目為100，交叉概率Pc為0.5，變異概率Pm為0.0001，最大遺傳代數為500。

1.4 模型驗證及應用域分析

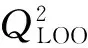
隨后采用威廉姆斯圖[26]對模型的應用域進行分析。威廉姆斯圖的橫軸為杠桿值，反映了某一樣本與訓練集中樣本在結構上的相似性，用hi表示。如果杠桿值hi大于警告杠桿值h*，則表明該樣本與訓練集樣本在結構上存在較大差異。警告杠桿值h*的計算公式如式(2)：

(2)

其中，p′表示用于建模的描述符個數；n′表示訓練集中樣本的總數量。

1.5 模型的機理解釋

為了明確篩選出的特征結構參數對辛烷值的影響程度大小，掌握其對辛烷值的影響規律，本研究中采用平均影響值法對所建模型中各描述符的相對重要程度進行評價，其計算公式如式(3)[27]：

(3)

式中，ME為平均影響值；J為模型中描述符的個數；aj表示第j個描述符的回歸系數；Dij為第j個描述符對于每個樣本的數值；m為描述符的個數。ME的符號為正值，表明該描述符與目標屬性呈正相關；ME符號為負值，表明該描述符與目標屬性呈負相關。ME的數值越大，表示該描述符對模型的影響越大；反之，描述符對模型的影響越小。

2 結果與討論

2.1 模型結果

針對訓練集樣本，應用GA-MLR算法對計算出的SiRMS描述符進行優化篩選和建模，確定與乙醇-汽油參比燃料混合物研究法辛烷值最為密切相關的2個分子碎片描述符，其名稱及含義見表3；最優描述符子集所對應的最佳MLR預測模型如式(4)所示：

(4)

式中，X11、X13為篩選出的分子碎片描述符；R2為模型復相關系數；RMSE為均方根誤差；n為訓練集樣本數；p為模型顯著性概率。

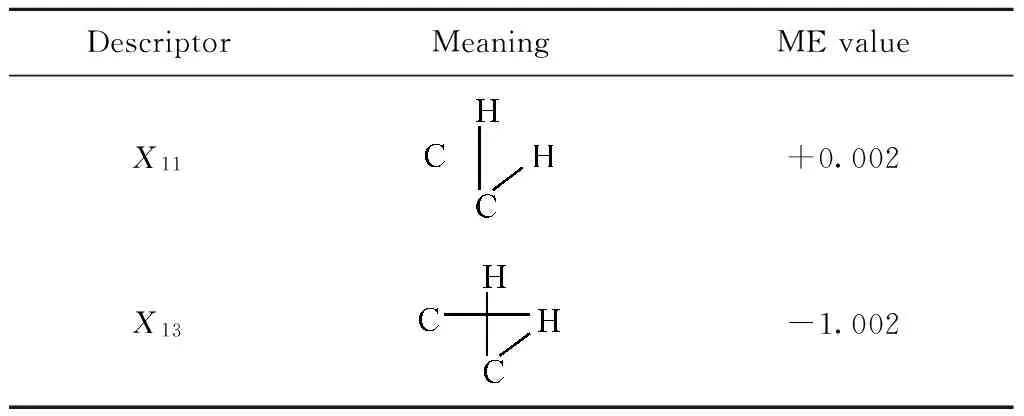
表3 RON模型篩選出的特征描述符及其含義Table 3 Meanings of the selected descriptors for prediction model of RON

隨后，應用所建模型對35個訓練集樣本進行校驗，以評價模型的擬合能力；同時，應用所建模型對未參與建模的測試集樣本進行預測，以驗證模型的外部預測能力。模型對所有樣本的預測值見表1，預測值與目標值的比較見圖1。

圖1 RON模型預測值與目標值的比較Fig.1 Comparisons between the predicted and observed RON values for the prediction model

2.2 模型的驗證

RON模型的主要性能參數見表4。從表4可以看出，對訓練集和測試集樣本的預測RMSE分別為1.840和1.925，誤差較小且較為接近，表明模型同時具有較優的預測能力及較強的泛化性能。

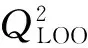
在此基礎上，對預測模型的殘差進行分析，結果見圖2。由圖2可見，樣本集樣本較為均勻地分布在0軸兩側，不存在明顯的規律性，表明模型建立過程中未產生系統誤差。

表4 RON模型的主要性能參數Table 4 Main performance parameters of prediction model of RON

AAE—Average absolute error； APE—Average percentage error； SE—Standard error

為了進一步對所建模型的穩定性進行分析，本研究應用“Y-隨機性檢驗”方法[28]對預測模型重復運行50次，得到相對最優模型的R2為0.032，不足原始模型R2的1/10。由此可見，只有在辛烷值與特征描述符一一對應時才能獲得準確可靠的預測模型，說明在本研究中所建立的預測模型不存在“偶然相關”現象，具備較強的穩定性。

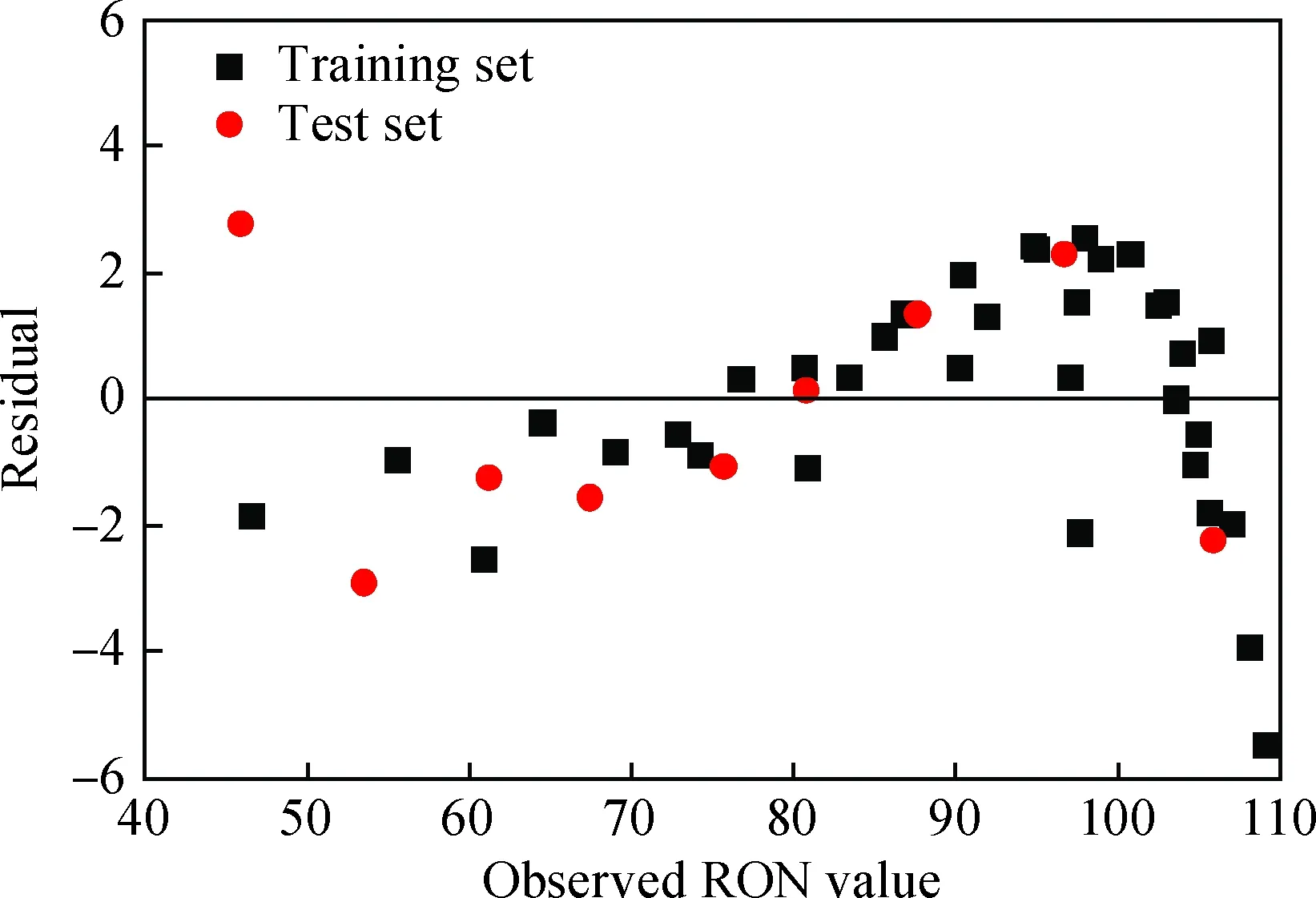
圖2 RON預測模型殘差圖Fig.2 Plot of the residuals versus the observed RON values for the prediction model

2.3 模型的應用域分析

為了確保模型對外部樣本預測結果的準確性和可靠性，需要對模型應用域進行分析，避免其產生不合理的預測結果，確保模型的外推能力。

本研究中采用威廉姆斯圖方法對模型的應用域進行分析，分析結果見圖3。其中，橫坐標為樣本杠桿值，縱坐標為樣本的標準化殘差。選取模型的3倍標準化殘差作為樣本預測殘差判斷界限。由圖3可知，模型的警告杠桿值h*為0.17，模型大部分樣本都位于警告杠桿值和殘差判斷界限所構成的矩形區域內，該區域即為預測模型的應用域，當預測模型對位于該區域內的樣本進行預測時，可以認為預測結果是有效、可靠的。

2.4 模型的機理解釋

為了進一步明確模型中各描述符對乙醇-汽油參比燃料混合物辛烷值的影響程度大小及規律，應用描述符重要度分析方法，對模型中各描述符的重要度進行比較和分析。

圖3 RON預測模型的威廉姆斯圖Fig.3 Williams plot for prediction model of RON

3 結 論

(1)對乙醇-汽油參比燃料混合物的研究法辛烷值開展了混合物的定量結構-性質相關性(M-QSPR)研究，應用SiRMS描述符對混合體系的分子結構特征進行表征，應用遺傳算法從大量描述符中優化篩選出與乙醇-汽油參比燃料混合物辛烷值最為密切相關的結構參數，建立了相應的辛烷值理論預測模型。模型驗證及穩定性分析結果表明，模型具有較優的預測能力和泛化性能，且穩定性較高。

(3)本研究為工程上提供了一種根據分子結構參數快速預測乙醇-汽油參比燃料混合物辛烷值的新方法。

[1] MARINOV N. A detailed chemical kinetic model for high temperature ethanol oxidation[J].International Journal of Chemical Kinetics, 1999, 31(2): 183-220.

[2] HEYWOOD J B. Internal Combustion Engine Fundamentals[M].New York: McGraw-Hill, 1988：723.

[3] FIENGO G, GAETA A D, PALLADINO A, et al. Introduction to Internal Combustion Engines[M].London： Springer London, 2013： 408-415.

[4] KALGHATGI G T. Fuel/Engine Interactions[M].Warrendale: SAE International, 2014： 201-231.

[5] ASTM D2699-08， Standard Test Method for Research Octane Number of Spark-Ignition Engine Fuel[S].

[6] ASTM D2700-14， Standard Test Method for Motor Octane Number of Spark-Ignition Engine Fuel[S].

[7] 仇愛波， 周如金， 邱松山， 等. 汽油組分及汽油辛烷值預測方法研究進展[J].天然氣化工(C1化學與化工)， 2014， 39(2)： 62-66. (QIU Aibo, ZHOU Rujin, QIU Songshan, et al. Review of octane number prediction methods for gasoline components and gasoline[J].Natural Gas Chemical Industry(C1 Chemistry and Chemical Industry), 2014,39(2)： 62-66.)

[8] GHOSH P, HICKEY K J, JAFFE S B. Development of a detailed gasoline composition-based octane model[J].Industrial & Engineering Chemistry Research, 2006, 45(1): 337-345.

[9] LUGO H J, RAGONE G, ZAMBRANO J. Correlations between octane numbers and catalytic cracking naphtha composition[J].Industrial & Engineering Chemistry Research, 1999, 38(5): 2171-2176.

[10] ALBAHRI T A, RIAZI M R, ALQATTAN A A. Analysis of quality of the petroleum fuels[J].Energy & Fuels, 2003, 17(3): 689-693.

[11] KARDAMAKIS A A, PASADAKIS N. Autoregressive modeling of near-IR spectra and MLR to predict RON values of gasolines[J].Fuel, 2010, 89(1): 158-161.

[12] 王宗明， 華偉英， 程桂珍， 等. 近紅外光譜法測定汽油辛烷值和辛烷值儀的研制[J].石油煉制與化工， 1997， 28(1)： 22-27. (WANG Zongming, HUA Weiying, CHENG Guizhen, et al. Determination of octane numbers of gasoline by FT-near infrared (FT-NIR) spectroscopy and the development of a FT-NIR octane number analyzer[J].Petroleum Processing and Petrochemicals, 1997,28(1)： 22-27.)

[13] 史月華， 陸勇， 徐光明， 等. 主成分回歸殘差神經網絡校正算法用于近紅外光譜快速測定汽油辛烷值[J].分析化學， 2001， 29(1)： 87-91. (SHI Yuehua, LU Yong, XU Guangming, et al. Principal component regression residual artificial neural network calibration algorithm applied in neat infrared fast measurement of gasoline octane number[J].Chinese Journal of Analytical Chemistry, 2001, 29 (1)： 87-91.)

[14] 朱曉， 蔣軍成， 潘勇， 等. 基于支持向量機方法的烷烴辛烷值預測[J].天然氣化工(C1化學與化工)， 2011， 36(3)： 54-57. (ZHU Xiao, JIANG Juncheng, PAN Yong, et al. Prediction of octane numbers of alkanes based on support vector machine[J].Natural Gas Chemical Industry (C1 Chemistry and Chemical Industry), 2011, 36(3): 54-57.)

[15] MEUSINGER R, MOROS R. Determination of quantitative structure-octane rating relationships of hydrocarbons by genetic algorithms[J].Chemometrics & Intelligent Laboratory Systems, 1999, 46(1): 67-78.

[16] LIU Zhefu, ZHANG Linzhou, ELKAMEL A, et al. Multiobjective feature selection approach to quantitative structure property relationship (QSPR) models for predicting the octane number of compounds found in gasoline[J].Energy & Fuels, 2017, 31(6): 5828-5839.

[17] 王寧， 徐亦方. 一種用拓撲指數和基團組成預測烷烴辛烷值的方法[J].石油學報(石油加工)， 1998， 14(3)： 67-73. (WANG Ning, XU Yifang. A new prediction method for antiknock of alkanes with topological indices and group composition[J].Acta Petrolei Sinica (Petroleum Processing Section), 1998, 14(3): 67-73.)

[18] HSIEH W D, CHEN R H, WU T L, et al. Engine performance and pollutant emission of an SI engine using ethanol-gasoline blended fuels[J].Atmospheric Environment, 2002, 36(3): 403-410.

[19] KAPUS P E, FUERHAPTER A, FUCHS H, et al. Ethanol direct injection on turbocharged SI engines-potential and challenges[C]//Detroit: SAE World Congress & Exhibition, 2007: 989-991.

[20] KAR K, CHENG W K, ISHII K. Effects of ethanol content on gasohol PFI engine wideopen- throttle operation[J].SAE International Journal of Fuels & Lubricants, 2009, 2(1): 895-901.

[21] ALRAMADAN A S, SARATHY S M, KHURSHID M, et al. A blending rule for octane numbers of PRFs and TPRFs with ethanol[J].Fuel, 2016, 180: 175-186.

[22] KUZ’MIN V E, ARTEMENKO A G, MURATOV E N. Hierarchical QSAR technology based on the simplex representation of molecular structure[J].Journal of Computer-Aided Molecular Design, 2008, 22(6-7): 403-421.

[23] MURATOV E N, VARLAMOVA E V, ARTEMENKO A G, et al. Existing and developing approaches for QSAR analysis of mixtures[J].Molecular Informatics, 2012, 31(3-4): 202-221.

[24] MERCADER A G, DUCHOWICZ P R, FERNNDEZ F M, et al. Replacement method and enhanced replacement method versus the genetic algorithm approach for the selection of molecular descriptors in QSPR/QSAR theories[J].Journal of Chemical Information & Modeling, 2010, 50(9): 1542-1548.

[25] TROPSHA A, GRAMATICA P, GOMBAR V. The Importance of being earnest: Validation is the absolute essential for successful application and interpretation of QSPR models[J].QSAR & Combinatorial Science, 2003, 22(1): 69-77.

[26] SAHIGARA F, MANSOURI K, BALLABIO D, et al. Comparison of different approaches to define the applicability domain of QSAR models[J].Molecules, 2012, 17(5): 4791-4810.

[27] 蔣軍成， 潘勇. 有機化合物的分子結構與危險特性[M].北京： 科學出版社, 2011： 224-226.

[28] RüCKER C, RüCKER G, MERINGER M. Y-randomization and its variants in QSPR/QSAR[J].Journal of Chemical Information & Modeling, 2007, 47(47): 2345-2357.