考慮節理影響的巖體非線性流變模型

曹平，黃磊，陳瑜，周科平，鄧紅衛

?

考慮節理影響的巖體非線性流變模型

曹平，黃磊，陳瑜，周科平，鄧紅衛

(中南大學 資源與安全工程學院，湖南 長沙，410083)

為研究節理巖體蠕變全過程，引入非線性黏性元件和節理裂隙塑性體，并將其與傳統的伯格斯模型串聯，得到一種新的復合流變模型。推導該模型一維和三維蠕變本構方程，并運用該復合模型及傳統伯格斯模型分別對巖石試樣蠕變實驗全過程曲線進行辨識，得到模型的各項蠕變參數。研究結果表明：復合流變模型對試驗數據的擬合結果明顯優于傳統伯格斯模型的擬合結果。該模型不僅能充分反映巖石試樣的初期蠕變和穩定蠕變過程，而且能很好地描述加速蠕變過程，同時又能體現節理裂隙對蠕變的影響。

巖石力學；復合流變模型；加速蠕變；節理裂隙；蠕變參數

巖體流變理論研究的是巖石或巖體在外力、水、溫度、地質特征及施工擾動等各種環境、地質與工程因素作用下，巖體材料、結構與時間相關的力學行為、本構關系、失穩與破壞規律。在巖石工程中，大多數失穩現象都與巖石的流變特性有關。巖石常常因受到外荷載長期的恒定作用而最終失穩，從而引發工程事故的發生，因此，對巖石流變力學特性的理論研究一直受到人們的重視。目前，已有一套較為完整的理論系統來表述巖石的流變特性，即通過基本變形元件(彈簧、阻尼器和摩擦元件)的不同串并聯組合模型來建立巖石的流變本構方程，常見的有麥克斯韋模型、開爾文模型、伯格斯模型、賓漢姆模型、西原模型等[1]，國內外研究者也對此進行了大量的研究[2?5]。然而，這些傳統的流變模型只能描述巖石的穩態蠕變，而不能描述加速蠕變過程，因此，具有一定的局限性。隨著巖體工程規模的不斷擴大和深部采礦的迅速發展，為保證工程的安全性，就需要能更好地反映巖石真實流變過程的新流變模型，因此，人們對流變理論的研究進入了非線性階段。目前，人們對于非線性流變理論的研究已經取得了不少成果，如：康永剛等[6?7]用分數單元代替伯格斯模型中并聯的黏壺，建立分數伯格斯模型，用來描述巖石的加速蠕變；宋勇軍等[8?9]將含分數階微積分的軟體元件與彈簧元件串聯，結合冪函數黏塑性體，提出一種新的四元件非線性黏彈塑性流變模型；曹樹剛等[10]將黏滯系數視作隨時間變化的變量，改進了西原模型；徐衛亞等[11?13]提出一種非線性黏塑性體(NVPB模型)，并將其與五元件線性黏彈性流變模型串聯起來，從而建立一種新的巖石非線性黏彈塑性流變模型；ZHOU等[14]將傳統西原模型中的2個線性黏壺均以非線性黏壺替代，并建立其微分形式的本構方程；BOUKHAROV等[15]提出用應力觸發的虎克體與應力觸發的非線性黏性元件組合而成的模型來描述加速蠕變。盡管人們在非線性流變方面取得了很大進展，但對一些問題的研究還不夠深入，如對節理巖體流變特性的研究還較少。節理巖體作為巖石工程中的常見研究對象，其強度、變形和破壞等特征直接影響到工程的穩定性，而這些特征往往體現出與時間的相關性，因此，節理巖體流變特性的研究對巖石工程具有重大意義。本文作者在伯格斯模型的基礎上，提出一種新的流變模型，用于描述巖石的加速蠕變過程，體現節理對巖石流變的影響。

1 新模型的建立

1.1 伯格斯模型

傳統伯格斯模型由虎克體、黏性體及黏彈性體組成，如圖1所示。其中：為該模型的總應力；0為彈性模量；1為黏性模量；1和2分別為黏壺的黏滯系數。該模型可以很好地模擬當應力小于屈服應力時巖石的流變特性，但不能描述巖石的加速蠕變。

圖1 伯格斯模型

1.2 非線性黏性元件

為描述巖石的加速蠕變過程，現引入1個非線性黏性元件[16]，如圖2所示。其中：nl為非線性黏性元件的黏滯系數。該元件具有應變觸發特性，即當應變小于a(即巖石結束穩態蠕變而開始進入加速蠕變時對應的應變)時，該元件呈現剛體的性質，而當應變大于a時，該元件開始發揮作用。定義該非線性黏性元件的本構關系為

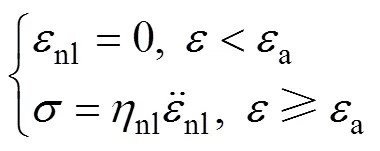
其中：nl為該元件進入加速蠕變后的應變。

(a) 非線性黏性元件；(b) 非線性元件蠕變曲線

圖2 非線性黏性元件及其蠕變曲線

Fig. 2 Nonlinear viscous component and its creep curve

1.3 節理裂隙塑性體

節理巖石中由于有大量微裂隙的存在，故其在受壓時存在一個微裂隙閉合的階段，該階段在宏觀上表現為巖石的塑性變形。夏才初[17]的研究結果表明：當實驗所加荷載達到某一特定值(應力門檻值)時，巖石試件因微裂隙閉合而產生的塑性變形開始顯現，而后隨荷載增加而逐漸增加，最終趨于穩定。為描述這種巖石蠕變過程中因節理微裂隙閉合而產生的塑性變形，現引入裂隙塑性體元件[18]，其結構如圖3所示。其中：隙裂性體由2條曲率按回旋線變化的單位長度等截面懸臂梁組成，2條梁相連于0曲率處，荷載作用于梁的末端，兩梁之間的間隙隨所加應力的增大而減小，當應力趨于無窮大時，間隙趨于0，此時，應變達到最大L，對應的應力為L，此裂隙塑性體的本構關系為

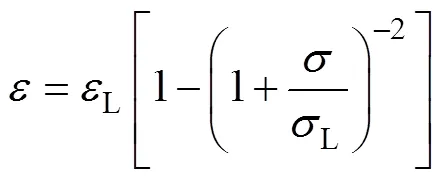
或

將該裂隙體與圣維南體并聯，用圣維南體的屈服強度s代替裂隙體的應力門檻值，如圖4所示。

(a) 裂隙塑性體；(b) 裂隙塑性體本構曲線

圖4 新型裂隙塑性體

1.4 節理巖體復合流變模型的建立

將非線性黏性元件、裂隙塑性體與傳統伯格斯模型串聯形成復合流變模型，以描述節理巖體的蠕變過程，如圖5所示。

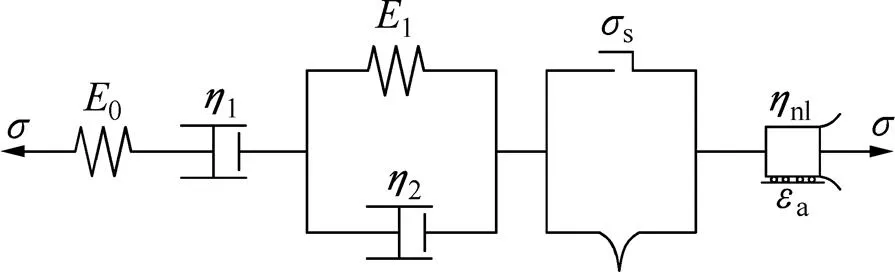
圖5 復合流變模型

當＜s時，非線性黏性元件表現為剛體，節理裂隙塑性體也未達到其應力門檻值，故均不發揮作用，此時復合流變模型退化為傳統伯格斯模型，其一維本構方程為

蠕變方程為

當≥s，＜a時，裂隙塑性體開始發生塑性變形，而非線性黏性元件仍表現為剛體，此時復合流變模型為傳統伯格斯模型與裂隙塑性體的串聯，由串、并聯關系可得

對上述各式進行Laplace變換，整理后再進行Laplace逆變換，可得在≥s，＜a條件下該流變模型的本構方程為

由串、并聯關系，并引入邊界條件=0，=0，可得模型的蠕變方程為

當≥s，≥a時，非線性黏性元件開始發揮作用，此時復合流變模型為傳統伯格斯模型、裂隙塑性體以及非線性黏性元件串聯而成的模型。

先單獨看非線性黏性元件，施加恒定荷載=0，當≥a時，由

可得

對式(10)進行積分，并由初始條件=a(即巖石開始進入加速蠕變階段對應的時刻)，nl0可得該黏性元件的蠕變方程為

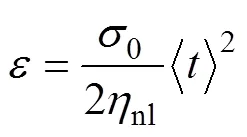
式中：

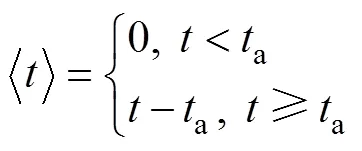
再由各元件之間的串聯關系可得復合流變模型的蠕變方程：

2 復合模型的三維蠕變本構關系

在實際工程中，巖石一般都處于復雜的三維應力作用下，而在室內試驗中也一般采用三軸壓縮試驗機進行巖石強度的測定，因此，建立巖石在三維應力作用下的蠕變本構關系具有重要的工程意義。

該復合流變模型可以看成是由虎克體、黏性體、黏彈性體、裂隙塑性體和非線性黏性體5部分串聯而成，在三維應力作用下，模型的總應變可以表示為

對于虎克體，由廣義虎克定律可知，虎克體的三維本構關系為

式中：，，和分別為應變偏量、應力偏量、應變和應力第一不變量的張量形式；0和分別為彈性剪切模量和彈性體積模量。

由此可得虎克體的應變為

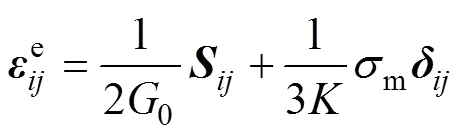
對于黏性體，在一維應力下，其本構方程為

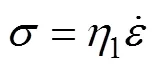
進而可得其蠕變方程為

三維情況下的應變可表示為

對于黏彈性體，假設該黏彈性體的體積變化是彈性的，其蠕變主要體現在剪切變形上，由此可知其三維本構關系為

對于裂隙塑性體，將一維情況下的應變推廣到三維狀態下可得

對于非線性黏性體，由于在室內的單軸或三軸壓縮蠕變試驗中，試樣在進入加速蠕變階段時大都體現在軸向變形急劇增大，因此，在三維應力狀態下，可以選擇第一主應力11與屈服強度a的關系來判斷非線性黏性體是否發生應變，當11≥a時，非線性黏性體開始觸發，試樣開始進入加速蠕變階段。由此，三維狀態下非線性黏性體的本構關系可以表示為

將式(14)~(21)代入式(13)，可得三維應力狀態下該復合模型的蠕變方程為

3 實驗數據擬合與驗證分析

本文作者根據文獻[19]中的實驗數據，對復合流變模型的蠕變方程進行擬合，以驗證該模型描述節理巖石蠕變全過程的合理性。將軟弱節理礦巖試樣加工成直徑×高度為50 mm×100 mm的標準圓柱形試件，利用剪切流變儀進行蠕變試驗。加載方式為循環加卸載，從小到大依次逐級施加荷載，荷載作用時間由試件應變率確定。當試件軸向應變在48 h內小于 0.01 mm時，可認為其達到穩定狀態，完全卸載，卸載后記錄其應變恢復；當試件在24 h內無應變恢復時再施加下一級荷載，依此類推，直至試件破壞為止。本文著重體現蠕變過程中的加速蠕變階段，故引用最高級荷載時的蠕變數據，此時荷載為33.8 MPa。

圖6所示為巖石試樣在實驗過程中的軸向應變?時間曲線。由圖6可知試樣的蠕變過程分為3個階段：0~1時間段為初期蠕變階段，1~a為穩定蠕變階段，a之后為加速蠕變階段。1=12.4 h，a=190 h，a所對應的應變可以看成是非線性黏性元件的應變觸發值a，a=9.92 mm。

圖6 巖石試樣軸向應變?時間曲線

根據復合模型的蠕變方程以及試樣應變?時間曲線，可將上述曲線分為2個部分：0~a時段曲線為第1部分，a之后的加速蠕變曲線為第2部分。對于第1部分曲線，對式(8)采用非線性最小二乘法，可以確定蠕變參數0，1，1和2。對于第2部分曲線，將確定好的0，1，1和2及裂隙塑性體元件的流變閾值參數[20]s=4.05 MPa，L=56.80 MPa和L=3.351 mm代入式(13)，并對其進行非線性最小二乘法可得蠕變參數nl。以上擬合過程可利用Origin軟件中自帶程序完成。

表1所示為復合模型對巖石試樣蠕變曲線辨識的所有蠕變參數。圖7所示為復合模型對巖石試樣蠕變過程曲線的擬合結果。由圖7可知：傳統伯格斯模型能較好地擬合穩定蠕變階段，但在擬合初期蠕變階段出現很大的偏差，尤其是在初始應變處，擬合值明顯低于試驗值，這是因為試件中含有節理裂隙，在受壓瞬間產生瞬時塑性變形，而傳統伯格斯模型中并沒有能描述這種因節理裂隙而造成的瞬時塑性變形的元件，同時，傳統伯格斯模型的擬合曲線中也并沒有體現出加速蠕變階段。而復合流變模型結果與實驗結果吻合良好，不僅能夠充分反映巖石的初期和穩定蠕變過程，而且能描述加速蠕變過程，同時，又能體現節理裂隙對蠕變的影響。

表1 復合流變模型參數

圖7 復合流變模型與伯格斯模型擬合曲線對比

4 結論

1) 引入1個非線性黏性元件，并將其與傳統伯格斯模型串聯，形成改進的伯格斯模型，以描述巖石蠕變的全過程。

2) 引入一種節理裂隙閉合體，用閉合體在外力作用下的變形來描述巖石中因節理裂隙閉合而引起的宏觀上的塑性變形，將其與改進的伯格斯模型串聯，形成新的復合流變模型，并推導出該模型在一維和三維應力狀態下的蠕變本構方程。

3) 新的復合流變模型的擬合結果明顯優于傳統伯格斯模型的擬合結果，不僅能充分反映巖石蠕變過程中的初期蠕變、穩態蠕變，而且能很好地描述加速蠕變，同時，也能體現節理裂隙對巖石蠕變的影響。

[1] 王芝銀, 李云鵬. 巖體流變理論及其數值模擬[M]. 北京: 科學出版社, 2008: 6?9. WANG Zhiyin, LI Yunpeng. Rock mass rheological theory and numerical simulation[M]. Beijing: Science Press, 2008: 6?9.

[2] LI Wenquan, LI Xiangdong, HAN Bing, et al. Recognition of creep model of layer composite rock mass and its application[J]. Journal of Central South University of Technology, 2007, 17(1): 329?331.

[3] FABRE G, PELLET F. Creep and time-dependent damage in argillaceous rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(6): 950?960.

[4] LIU Lang, WANG Geming, CHEN Jianhong. Creep experiment and rheological model of deep saturated rock[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(2): 478?483.

[5] 張春陽, 曹平, 汪亦顯, 等. 自然與飽水狀態下深部斜長角閃巖蠕變特性[J]. 中南大學學報(自然科學版), 2013, 44(4): 1587?1595. ZHANG Chunyang, CAO Ping, WANG Yixian, et al. Creep characteristics of plagioclase hornblende rock under natural and water-saturated conditions in deep underground[J]. Journal of Central South University(Science and Technology), 2013, 44(4): 1587?1595.

[6] 康永剛, 張秀娥. 巖石蠕變的非定常分數伯格斯模型[J]. 巖土力學, 2011, 32(11): 3237?3241. KANG Yonggang, ZHANG Xiue. Nonstationary parameter fractional Burgers model of rock creep[J]. Rock and Soil Mechanics, 2011, 32(11): 3237?3241.

[7] 康永剛, 張秀娥. 基于Burgers模型的巖石非定常蠕變模型[J]. 巖土力學, 2011, 32(S1): 424?427. KANG Yonggang, ZHANG Xiue. A non-stationary model for rock creep based on Burgers model[J]. Rock and Soil Mechanics, 2011, 32(S1): 424?427.

[8] 宋勇軍, 雷勝友, 韓鐵林. 一種新的巖石非線性黏彈塑性流變模型[J]. 巖土力學, 2012, 33(7): 2076?2080. SONG Yongjun, LEI Shengyou, HAN Tielin. A new nonlinear viscoelasto-plastic rheological model for rocks[J]. Rock and Soil Mechanics, 2012, 33(7): 2076?2080.

[9] 宋勇軍, 雷勝友. 基于分數階微積分的巖石非線性蠕變損傷力學模型[J]. 地下空間與工程學報, 2013, 9(1): 91?95. SONG Yongjun, LEI Shengyou. Mechanical model of rock nonlinear creep damage based on fractional calculus[J]. Journal of Underground Space and Engineering, 2013, 9(1): 91?95.

[10] 曹樹剛, 邊金, 李鵬. 巖石蠕變本構關系及改進的西原正夫模型[J]. 巖石力學與工程學報, 2002, 21(5): 632?634. CAO Shugang, BIAN Jin, LI Peng. Rheologic constitutive relationship of rocks and a modifical model[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(5): 632?634.

[11] 徐衛亞, 楊圣齊, 褚衛江. 巖石非線性黏彈塑性流變模型(河海模型)及其應用[J]. 巖石力學與工程學報, 2006, 25(3): 433?447. XU Weiya, YANG Shengqi, CHU Weijiang. Nonlinear viscoelasto-plastic rheological model (HoHai model) of rock and its engineering application[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(3): 433?447.

[12] 徐衛亞, 楊圣齊, 楊松林, 等. 綠片巖三軸流變力學特性的研究(I): 試驗結果[J]. 巖土力學, 2005, 26(4): 531?537. XU Weiya, YANG Shengqi, YANG Songlin, et al. Investigation on triaxial rheological mechanical properties of greenschist specimen(I): experimental results[J]. Rock and Soil Mechanics, 2005, 26(4): 531?537.

[13] 徐衛亞, 楊圣齊, 謝守益, 等. 綠片巖三軸流變力學特性的研究(II): 模型分析[J]. 巖土力學, 2005, 26(5): 693?698. XU Weiya, YANG Shengqi, XIE Shouyi, et al. Investigation on triaxial rheological mechanical properties of greenschist specimen(II): model analysis[J]. Rock and Soil Mechanics, 2005, 26(5): 693?698.

[14] ZHOU Hongwei, WANG C P HAN B B, et al. A creep constitutive model for salt rock based on fractional derivatives[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(1): 116?121.

[15] BOUKHAROV G N，CHANDA M W，BOUKHAROV N G. The three processes of brittle crystalline rock creep[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1995, 32(4): 325?335.

[16] 齊亞靜, 姜清輝, 王志儉, 等. 改進西原模型的三維蠕變本構方程及其參數辨識[J]. 巖石力學與工程學報, 2012, 31(2): 347?355. QI Yajing, JIANG Qinghui, WANG Zhijian, et al. 3D creep constitutive equation of modified Nishihara model and its parameters identification[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 347?355.

[17] 夏才初. 軟巖的流變性及其尺寸效應的研究[D]. 長沙: 中南工業大學資源環境與建筑工程學院, 1987: 33?34. XIA Caichu. Research on rheology of soft rock and its size effect[D]. Changsha: Central South University of Technology. College of Resources, Environment and Civil Engineering, 1987: 33?34.

[18] 陳浣江, 潘長良, 曹平, 等. 一種軟巖流變模型[J]. 中南工業大學學報(自然科學版), 2003, 34(1): 16?20. CHEN Yuanjiang, PAN Changliang, CAO Ping, et al. A new rheological model for soft rocks[J]. Journal of Central South University of Technology (Natural Science), 2003, 34(1): 16?20.

[19] ZHAO Yanlin, CAO Ping, WEN Weijun, et al. Viscoelasto-plastic rheological experiment under circular increment step load and unload and nonlinear creep model of soft rocks[J]. Journal of Central South University of Technology, 2009, 16(3): 488?494.

[20] 王永巖, 魏佳, 齊珺, 等. 深部巖體非線性蠕變變形預測的研究[J]. 煤炭學報, 2005, 30(4): 409?413. WANG Yongyan, WEI Jia, QI Jun, et al. Study on prediction for nonlinear creep deformation of deep rocks[J]. Journal of China Coal Society, 2005, 30(4): 409?413.

(編輯 伍錦花)

Nonlinear rheological model of rock considering the effects of joints

CAO Ping, HUANG Lei, CHEN Yu, ZHOU Keping, DENG Hongwei

(School of Resource and Safety Engineering, Central South University, Changsha 410083, China)

To study the whole creep process of jointed rock, nonlinear viscous element and joint fissures plastic body were introduced, and then combined with classical Burgers model in series to gain a new composite creep model. 1D and 3D creep constitutive equation of the composite creep model were deduced. By using the composite creep model and the classical Burgers model to fit with the whole process of rock specimen creep curve, creep parameters of the models were derived. The results show that the composite creep model produces better fitting results than the classical Burgers model. It can not only fully reflect the early and steady creep process, but also well present the accelerating creep process of the rock specimen. Meanwhile, it can also reflect the influence of joint fissures on creep.

rock mechanics; the composite creep model; accelerating creep; joint fissures; creep parameters

10.11817/j.issn.1672?7207.2018.02.019

TU45

A

1672?7207(2018)02?0401?06

2017?03?21；

2017?05?30

國家自然科學基金資助項目(11772358，51604299，51774323，51274249)；湖南省研究生科研創新項目(CX2012B069)；中國博士后科學基金資助項目(2016M600636)；中南大學博士后科學基金資助項目(2017)；國家重點研發計劃項目(2016YFC0600706) (Projects(11772358, 51604299, 51774323, 51274249) supported by the National Natural Science Foundation of China; Project(CX2012B069) supported by the Postgraduate Innovative Research Project of Hunan Province; Project(2016M600636) supported by China Postdoctoral Science Foundation; Project(2017) supported by Central South University Postdoctoral Science Foundation; Project (2016YFC0600706) supported by the National key Research and Development Program)

曹平，博士，教授，博士生導師，從事巖石力學與工程領域的教學和科學研究工作；E-mail: pcao_csu@sohu.com