借幾何直觀 促深度理解 育數學素養

芮金芳

【關鍵詞】幾何直觀；深度理解；核心素養

【中圖分類號】G623.5 【文獻標志碼】A 【文章編號】1005-6009（2018）01-0066-03

幾何直觀作為新課標提出的十大核心概念之一，是學生發展中的必備數學素養，在其數學學習中發揮著重要的作用。幾何直觀主要指利用圖形描述問題、分析問題，借助幾何直觀能把復雜的數學問題變得簡明、形象，有助于學生探索解決問題的思路、預測結果。幾何直觀能幫助學生直觀地理解數學，使他們形成一種數形結合洞察世界的能力，培育其創造性的數學思維方式。所以，在數學教學中要注意發揮幾何直觀的獨特價值，培養學生的幾何直觀能力，提升其數學綜合素養。

1.借助幾何直觀，生動表征數學概念。

數學概念的形成是抽象、理性的。小學生的思維正處于由具體形象思維向抽象邏輯思維過渡的階段，而且在過渡的過程中需要具體表象的支撐。所以，在學習概念時需要幾何直觀提供具體、直觀的支撐。如教學蘇教版三上《分數的初步認識》一課時，教師提供幾個不同的圖形（如圖1），讓學生通過折一折、涂一涂表示出它們的二分之一，然后組織學生交流操作結果，從而提煉出二分之一的本質屬性。

師：大家展示的圖形都不同，為什么涂色部分都能用二分之一來表示呢？

生：不管圖形的形狀如何，只要把它平均分成兩份，涂色部分是其中的一份，就表示這個圖形的二分之一。

這是學生建立二分之一概念的重要環節。學生從具體實物（分一個蛋糕）的二分之一開始，逐步抽象到一個圖形的二分之一，在不同圖形的觀察比較中，舍棄事物非本質、次要的特征，聚焦概括出“都是平均分成兩份，取其中的一份”這一本質特性。教師引導學生將數譯成形，再用語言表征描述所畫圖形的含義，使得學生把頭腦中形成的二分之一的表象進行視覺化，增強了學生借助直觀圖形表征數學概念的能力，豐富了學生的數感，同時提升了他們運用幾何直觀形象、直觀地刻畫抽象概念的能力。

在數學學習中，由于受到已有經驗和思維水平的限制，學生經常會遇到用語言表達不清的尷尬情形。這時，圖形直觀會成為學生最有效的表達工具。充分利用直觀材料和幾何形象能為學生提供自主思考、深度學習的思維路徑。利用幾何圖形能清楚、直觀地表達出數與數之間的關系，讓學生在圖形表征中發現積的分子和分母與兩個因數的分子、分母之間的內在關系，自主建構分數乘分數的算法，并借助直觀圖示理解其算理。類似地，在學習整數加減法、小數乘除法、分數加減法時也都可以利用圓片、正方體模型、方格圖等圖形直觀來表征運算過程的意義，同時以形助數更深入地理解其算理。

3.借助幾何直觀，提升問題解決能力。

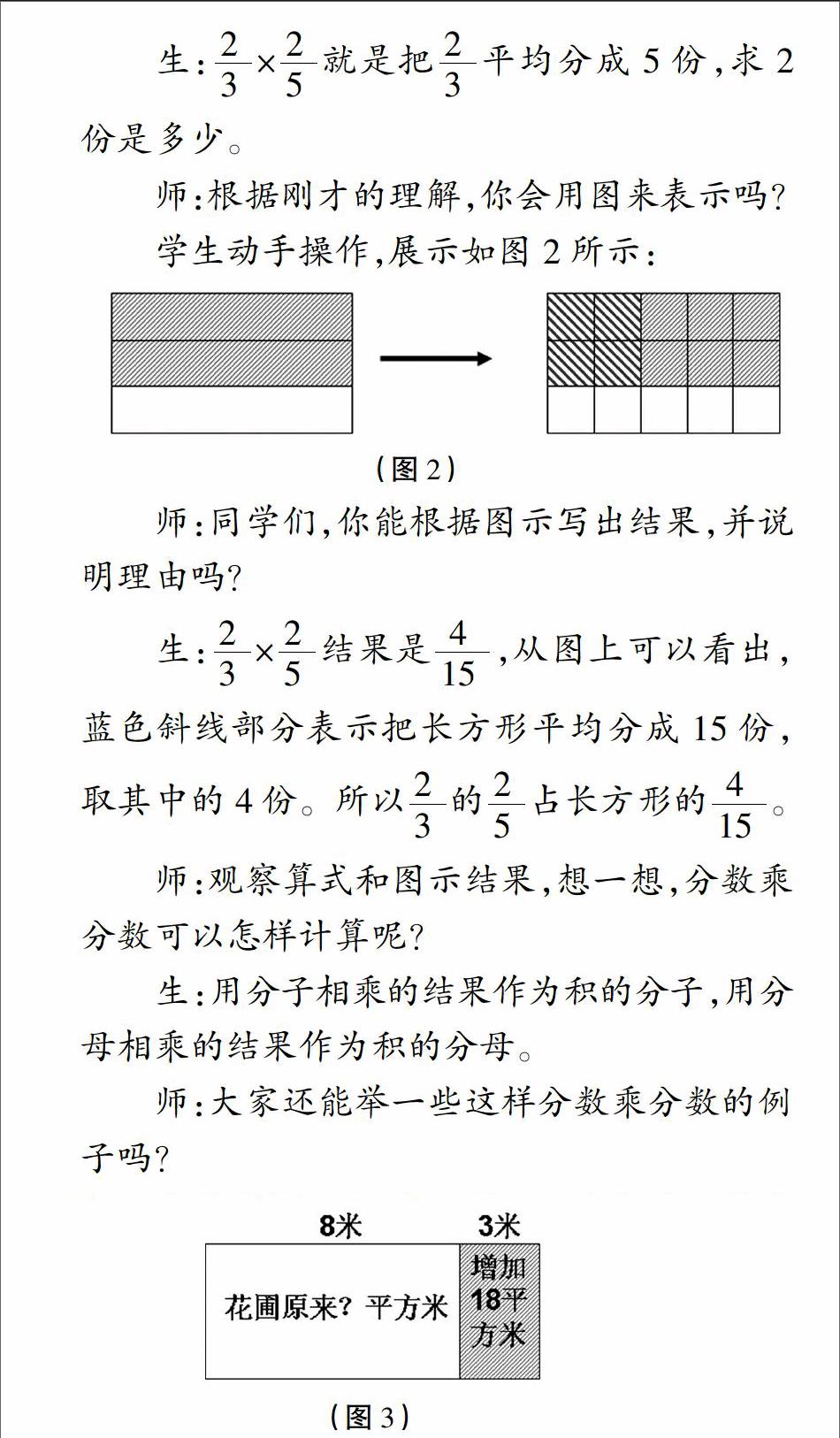
數學問題一般由問題情境信息及其內在關系要素組成。要正確地解決數學問題，必須透過信息表層達到對數學問題結構性的理解。但有些數學問題的呈現形式過于煩瑣，學生無法從文字的敘述和解讀中抓住其中的核心關系，而難以將問題轉化成自身可以理解的內容。例如：教學蘇教版四上《解決問題的策略：畫圖》一課，有這樣一個實際問題：“梅山小學有一塊長方形花圃，長8米。在修建校園時，花圃的長增加了3米，這樣花圃的面積就增加了18平方米。原來花圃的面積是多少平方米？”面對這樣復雜、冗長、抽象的實際問題，如果直接進行解答，學生很難找到數量之間的關系，在這樣的認知沖突下，會自然引發他們畫圖（面積示意圖）的內在學習需求。在學生用示意圖（如圖3）清楚、完整、簡潔地表示出信息后，讓他們對文字和示意圖進行比較，深度感受畫直觀示意圖的價值。在這里，幾何直觀起到啟迪學生思考解題思路的作用，學生在層層分析、推理、解決問題的過程中，不但可以深刻感受到畫圖策略的重要地位，而且能充分體會畫面積示意圖對描述、整理問題和探尋、分析問題解決思路的價值和作用。

4.借助幾何直觀，發展推理想象能力。

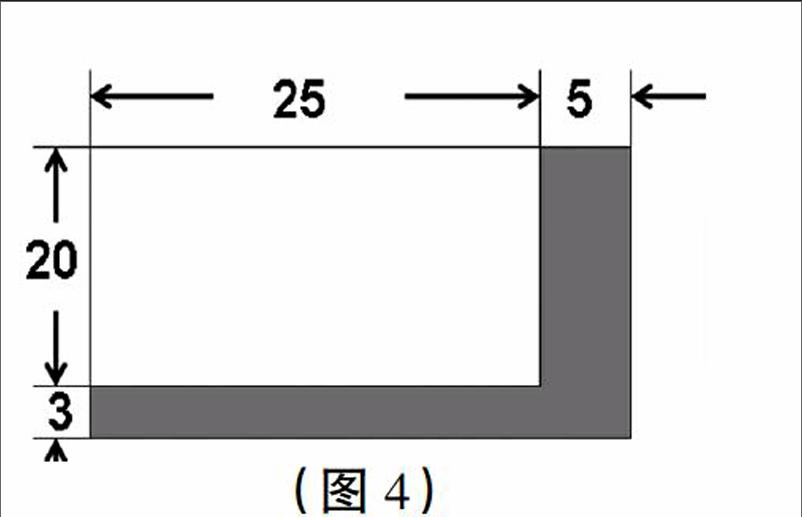
直觀推理是一種滲透性極強的思維形式，可以看作數學直觀的精髓。加強幾何直觀教學并不單單要求學生能夠利用示意圖或線段圖直觀表征數、數量之間的關系，還要能利用圖形產生新的認識，或借助圖形進行直觀推理，從而洞察各個對象之間的結構關系，獲得直觀、系統、整體性的認識。如：（1）小劇場原來每排有25個座位，有20排。擴建后每排增加5個座位，增加3排。擴建后共增加了多少個座位？（2）原計劃買25個球，每個20元。實際每個漲價3元，而且多買了5個。實際比計劃多用多少元？（3）一個長方形種植園長25米，寬20米。擴建后長增加5米，寬增加3米。擴建后的面積增加了多少平方米？乍一看，這三道題似乎毫不相干，情境內容各異，但深入思考后會發現它們的內在數量關系是一致的，可以用相同的幾何模型來表達，如圖4所示。所以，除了依據常規數量之間的關系列式（25+5）×（20+3）-25×20以外，根據長方形面積示意圖的直觀表達和劃分，學生還能輕松地得到另外兩種解法：5×（20+3）+25×3和（25+5）×3+20×5。這些多樣化的思考和表達是學生借助幾何直觀進行比較、分析、推理和想象逐步形成的。從這個角度看，是一種創造性的數學思維。借助幾何圖形，學生能由淺入深、由表及里地展開想象，創造性地進行探究活動。

荷蘭數學家弗賴登塔爾曾說過：幾何直觀能告訴我們什么是可能重要、可能有意義和可接近的，并使我們在課題、概念和方法的荒漠之中免于陷入歧途之苦。可見，幾何直觀可以幫助我們很好地把握問題的本質。作為學生必備的一種數學素養，幾何直觀的形成不是一蹴而就的，需要教師在教學中不斷滲透幾何直觀的意識，教會學生圖形直觀的表達方法，使學生逐步積累幾何直觀表達的經驗，提升其運用幾何直觀的能力。

【參考文獻】

[1]中華人民共和國教育部.義務教育數學課程標準（2011年版）[S].北京：北京師范大學出版社，2012.

[2]王林，等.小學數學課程標準研究與實踐[M].南京：江蘇教育出版社，2011.

[3]蔡宏圣.幾何直觀：小學數學教學的視角[J].課程·教材·教法，2013（5）：109-115.

（作者單位：江蘇省溧陽市外國語學校）endprint