基于有限元模型的噴氣渦流紡纖維運動軌跡模擬

韓晨晨， 程隆棣， 高衛東， 薛 元， 楊瑞華(. 生態紡織教育部重點實驗室(江南大學)， 江蘇 無錫 4； . 東華大學 紡織面料技術教育部重點實驗室， 上海 060)

噴氣渦流紡紗技術在氣流加捻腔內利用高速旋轉氣流流場加捻自由端纖維成紗，其速度最高可達500 m/min，省去了粗紗環節，集細紗、絡筒、卷繞成形工序于一體，縮短了紡紗流程，是一種具有市場前景的新型紡紗技術[1]。Basal等[2]基于純棉紗線，分析了纖維內外轉移和噴氣渦流紡紗工藝參數的相關性；Tyagi等[3]基于滌棉纖維原料，以實驗的研究方法分析得到了噴嘴壓力、前羅拉鉗口與空心錠子入口距離和紡紗速度等對紗線組成比例和紗線結構分類的影響；李永霞[4-5]在日本村田噴氣渦流紡紗設備的基礎上，對關鍵成紗部件進行了設計和改進，噴孔數目增加到6個，實驗確定紡純棉原料的最佳噴嘴參數，探討設計改良后的噴嘴結構參數對成紗結構、成紗性能的影響；俞兆昇[6]研究發現了噴氣渦流紡空心錠錐面傾斜角度與自由端纖維倒伏狀態、噴氣渦流紡紗線組成結構纖維比例的相關性；Ortlek等[7]分析研究了關鍵成紗部件—空心錠的結構，包括內部紗線通道的直徑和外部表面的平滑程度等對成紗性能的影響；Liu等[8]運用Zeng-He模型，分析計算了噴氣渦流紡紗技術氣流強度與纖維氣流加捻強度的相關性；Guo等[9]基于對噴氣渦流紡氣流加捻腔內的二維標準湍流流場模型，模擬分析了空心錠錐面傾斜角對流場分布特征的影響；鄒專勇等[10]基于Fluent三維流體力學模擬，分析了噴氣渦流紡成紗工藝參數和關鍵成紗部件結構對氣流加捻腔內高速旋轉氣流的影響，進而得到其與成紗結構、性能的關系。

由于噴氣渦流紡氣流加捻腔的不規則性、不可視性及較小尺寸，均為捕捉流場中纖維運動圖像帶來了困難，目前國內外研究主要從流場模擬和實驗角度間接、定性地對噴氣渦流紡成紗機制、紗線結構及成紗工藝與紗線結構的相關性等方面進行探討。本文針對噴氣渦流紡氣流加捻過程中自由端纖維柔性體的運動特點，基于彈性細桿單元建立纖維柔性體有限元模型；結合噴氣渦流紡氣流加捻腔內流場的氣壓、速度分布特征，確立自由端纖維柔性體有限元動力學微分方程，遵循力學平衡、能量守恒、質量守恒和動量守恒等原理，解析自由端纖維柔性體有限元動力學微分方程的待定系數，數值模擬自由端纖維在加捻腔內高速旋轉氣流作用下的運動軌跡；最后利用示蹤纖維法對有限元模擬纖維運動軌跡的理論結果進行驗證。本文研究結果可為研究噴氣渦流紡成紗過程和原理提供新的思路。

1 有限元模型建立與動力學分析

纖維是一種具有較大長徑比、一定彈性和柔性的細長體，其在高速加捻氣流場中的實際運動規律非常復雜，涉及平動、轉動、彎曲、拉伸、扭轉等，現有的研究中通常將纖維柔性體的特殊結構作了相關簡化，以便對其運動特點進行分析[11]，例如非球形的剛性粒子纖維模型、多剛體鏈式纖維模型、珠-桿式纖維模型等一般都只將纖維柔性體看作二維的空間曲線，不考慮纖維的直徑、纖維運動過程中截面的扭轉變形，從而不能直接、定量地表征纖維在氣流場中的真實運動規律[12]。本文基于纖維柔性體的材料特性，結合噴氣渦流紡氣流加捻腔內自由端纖維柔性體的空間運動特點，根據力學平衡、動量守恒和能量守恒原理，將噴氣渦流紡氣流加捻腔內自由端纖維繞空心錠表面的高速旋轉運動轉化為空間彈性細桿的幾何非線性變形。

1.1 單纖維有限元模型的建立

本文基于彈性細桿單元建立纖維有限元模型，將單根纖維柔性體分為n個剛性微元段n+1個節點，每個剛性微元段看作一般空間運動的剛體，整體空間結構如圖1所示。取其中每個剛性微元段的中點處橫截面為研究對象，以固定不動的地面為參照物，過截面中心建立坐標系，由此可見，每個剛性微元段有6個自由度，通過計算解析獲得6個自由度所對應的坐標參數，進而確定每個剛性微元段的相對位置，描述每個剛性微元段的彎曲、拉伸和扭轉運動。

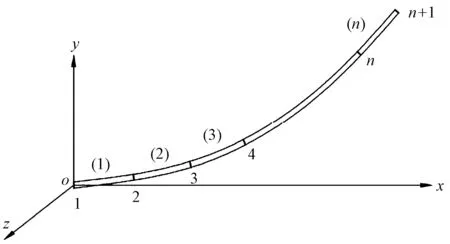
圖1 彈性細桿有限元模型整體空間示意圖Fig.1 Elastic thin rod finite element model in overall space

單根纖維柔性體有限元模型上的剛性微元段如圖2所示。圖中：o-xyz為以固定不動的地面為參照物建立的總體坐標系，o′-uvw為隨剛性微元段運動的子坐標系，即節點坐標系；節點坐標系的坐標原點位于剛性微元段中點處截面的圓心，u軸與剛性微元段軸向方向一致，v和w軸位于剛性微元段中點處的截面上。

圖2 剛性微元段坐標系示意圖Fig.2 Coordinate system of infinitesimal rigid segments

1.2 單纖維的動力學分析

在單纖維有限元模型動力學分析過程中，本文做了以下相關假設，以實現該動力學分析的有效性：1)不考慮纖維運動對流場分布的影響；2)流場對纖維的作用力看作是連續的且均勻作用于纖維的表面上。

根據牛頓定律[14]可知，單根纖維有限元模型上的剛性微元段的動力學微分方程為

(1)

式中：m為剛性微元段的質量；(ax,ay,az)為剛性微元段相對于o-xyz的加速度；(Fx,Fy,Fz)為作用于剛性微元段表面矢量的作用力。

對于固結于每個節點的剛性微元段，將其節點自由度符號轉換成總體節點自由度符號，用每個節點的6個自由度表示動力學方程，則有：

(2)

相對于固定不動的地面的整體坐標系，則有：

(3)

單根纖維柔性體有限元模型分析，結合以上公式可得，每根纖維柔性體運動所需的作用力為

(4)

式中：{Q}為加在節點上的作用力，共有6 (n+1)個分量。

2 數值模擬單纖維的運動規律

2.1 數值模擬的參數設置

提取流體力學模擬所得噴氣渦流紡加捻腔內高速旋轉氣流分布數據[13]如圖3所示。將自由端纖維看作是長為38 mm、半徑為0.006 mm的細長圓柱體，基于ANSYS軟件單元庫中SOLID45結構單元建立，設置材料密度為1.58 g/m3，泊松比為0.35，彈性模量為4.6×1011Pa，模型遵循線彈性本構關系，預拉應力為0 kN，極限拉應變取為0.01。將空心錠看作相對固定的剛體，自由端纖維柔性體頭端的約束看作固定約束，將空氣阻力F看作自由端纖維柔性體彈性細桿所受的載荷，分析計算自由端纖維柔性體在空氣阻力F載荷作用下的幾何非線性變形和靜平衡形態。

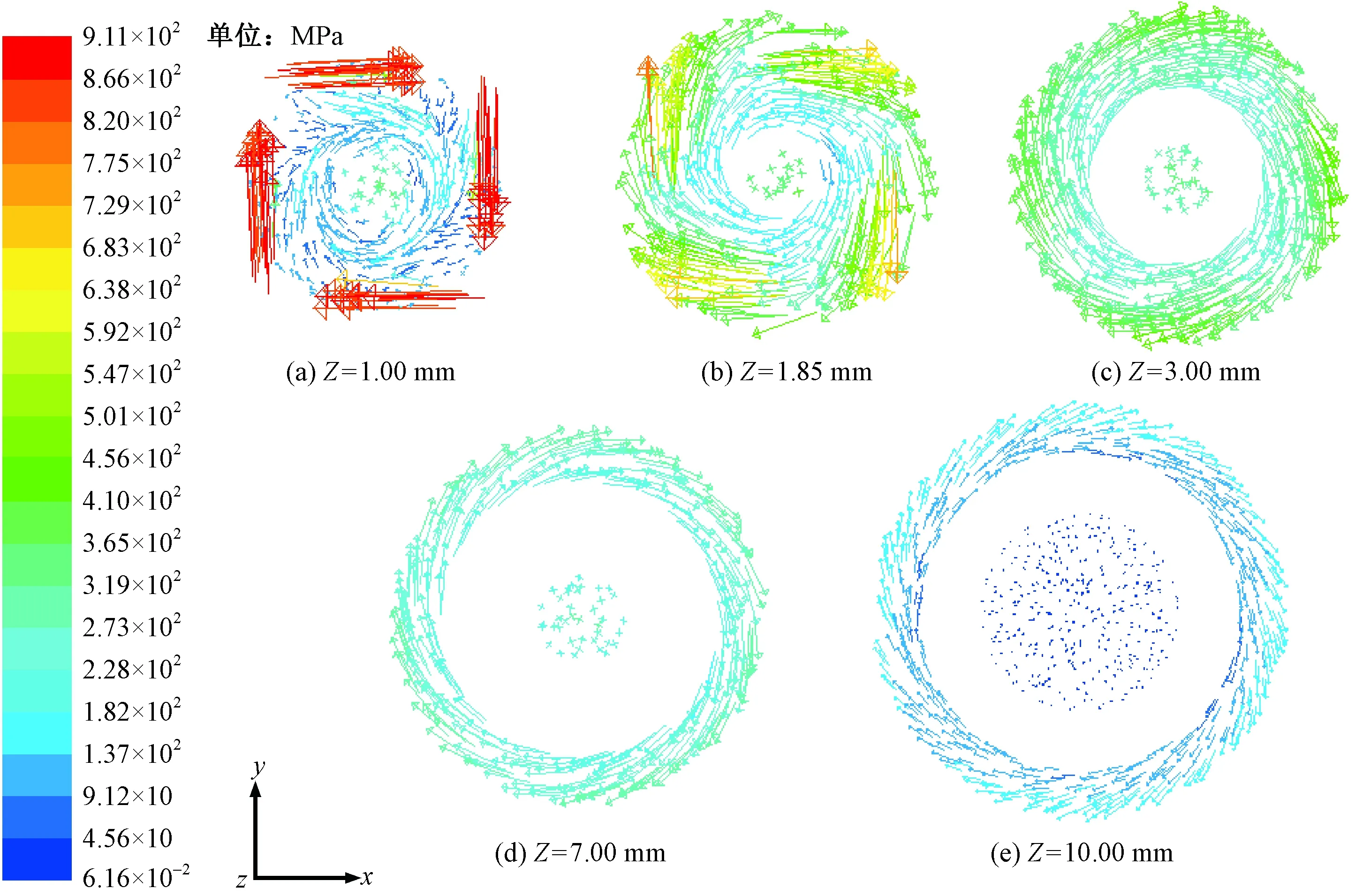
圖3 氣流加捻區不同Z坐標值平面上氣流速度矢量圖Fig.3 Airflow velocity on plane of different Z-coordinate in air-jet twisting zone

劃分實體網格采用規則的正六面體。設置Relevance Center為Fine，Element Size 為0.001，Smoothing為High，Transition為Fast，Span Angle Center為Fine，Minimum Edge Length為1×10-6m，其他均為默認值。自由端纖維柔性體與空心錠表面之間的壁面處理，約束條件遵循罰函數規律，當自由端纖維柔性體在繞空心錠表面作旋轉運動時，罰函數會在自由端纖維柔性體和空心錠表面接觸的位置處設置一個排斥力，這個排斥力的特點是隨著自由端纖維柔性體和空心錠表面間的距離減小到一定范圍時迅速增大，隨著自由端纖維柔性體和空心錠表面間的距離增大超過該范圍內時迅速減小為0，這樣就可以避免在數值模擬計算過程中，自由端纖維柔性體進入到空心錠內部。在模型柱底面施加xyz方向自由度的約束Fixed Support，在模型頂面設置均布的切向位移約束，Displacement為720°，沿纖維軸向Z軸施加自由度約束，Displacement為0 m。設置載荷步長的時間為0.01 s，荷載步數為200。在分析中，纖維長度方向為Z軸，徑向方向為x、y軸。運用MatLab軟件編程計算，收斂精度設置為0.05，迭代次數設置為50次。求得自由端纖維柔性體在空氣阻力F載荷作用下繞空心錠表面旋轉運動過程中的幾何非線性變形和靜平衡形態如圖4所示。

圖4 自由端纖維繞空心錠頂端錐形曲面旋轉時的運動軌跡Fig.4 Trajectory of free-end fiber around top of hollow spindle

2.1 自由端纖維的運動速度

由數值模擬結果中提取得到自由端纖維柔性體的運動速度分布規律如圖5所示。H在0～5.25 mm范圍內，自由端纖維柔性體的運動速度隨著H的增大而增大，在H=5.25 mm時，自由端纖維柔性體的運動速度達到最大，H在5.25～11.15 mm 范圍內，自由端纖維柔性體的運動速度隨著H的增大而減小。如圖4所示，空心錠頂端結構的錐形曲面傾斜程度在H=5.25 mm處變大，即空心錠頂端錐形曲面上基線與空心錠軸線間的夾角變大，進而影響自由端纖維柔性體軸線與空心錠頂端錐形曲面上基線間的夾角，使自由端纖維柔性體的運動規律在H=5.25 mm處發生轉折。利用Origin軟件分段擬合自由端纖維柔性體在不同位置處不同方向上的運動速度，得式(5)～(7)。

圖5 自由端纖維柔性體在不同位置處不同方向上的運動速度分布規律Fig.5 Distribution of free-end fiber velocity

自由端纖維柔性體在不同位置處切線方向上的運動速度vTa計算式為

(5)

在H≤5.25 mm的范圍內，自由端纖維柔性體在不同位置處徑向上的運動速度較小影響不大，可忽略不計；在H≥5.25 mm的范圍內，自由端纖維柔性體在不同位置處徑向上的運動速度vRa計算為

(6)

自由端纖維柔性體在不同位置處軸線方向上的運動速度vAa計算式為

(7)

2.2 自由端纖維的運動軌跡

由于空心錠頂端曲面結構參數變化，自由端纖維柔性體各剛性微元段在不同區域內的空間位置計算如式(8)～(10)所示。

在0 mm

(8)

在5.25 mm≤H<11.15 mm區域內，自由端纖維柔性體各剛性微元段的三維位置為

(9)

式中：φ為自由端纖維柔性體各剛性微元段螺旋傾斜因數；r1為H=5.25 mm處空心錠外表面直徑；δ為空心錠頂端錐形曲面上基線與空心錠軸線間的夾角(0 mm

自由端纖維柔性體的運動軌跡為

(10)

0

3 實驗驗證

3.1 實驗參數

紗線原料均為粘膠纖維，長度為38 mm，線密度為1.3 dtex，由奧地利蘭精公司生產；紗線規格為19.4 tex和14.5 tex，由MVS870設備生產，紡紗工藝參數如表1所示，粗紗定量為360 g/(5 m)，粗紗回潮率為11%，條于不勻率≤2%。紡紗車間相對濕度為(65±3)%，溫度為(20±2)℃。選取一定長度的樣紗制作實驗標本，將樣紗兩端固定在觀察玻璃片上，保持樣紗上所觀察部位原本的結構形態不受破壞，將制作好的19.4 tex和14.5 tex樣紗實驗標本做熱定型處理，處理溫度為135 ℃，處理氣體為飽和水蒸汽，處理時間為30 min，樣紗中粘膠纖維的化學結構受到熱定型處理后將發生變化，該變化為不可逆的，這樣經過濕熱處理后的樣本紗線將發生永久性定型，使得紗線的結構形態能夠在觀察實驗過程中得到較好地保持。將紗線置于Hi-Scope顯微鏡下觀察，放大倍數為160。

表1 成紗工藝參數Tab.1 Process parameters

3.2 實驗結果分析

噴氣渦流紡紗線成形速度高達450 m/min，且因成形過程封閉，無法通過攝像裝置觀察纖維實際運動狀態。加捻腔內高速旋轉氣流作用下倒伏在空心錠入口的自由端纖維柔性體的運動規律與紗線中纖維柔性體的空間分布形態構象具有一致性，因此討論噴氣渦流紡單纖維柔性體運動特征可轉化為研究紗線結構中纖維柔性體的空間分布形態構象。19.4 tex和14.5 tex噴氣渦流紡紗線表面結構如圖6、7所示，19.4 tex噴氣渦流紡紗線的表面包纏角平均值為47.5°，14.5 tex噴氣渦流紡紗線的表面包纏角平均值為42.5°。與理論數值模擬結果對比，噴氣渦流紡紗線樣紗表面包纏角測得較小，這主要是因為理論數值模擬過程中忽略了實際氣流加捻成紗過程中，自由端纖維運動受到來自氣流，空心錠表面，纖維之間的摩擦阻力作用，實驗測試結果的誤差在合理范圍內。所以在一定范圍內，驗證了彈性桿有限元模型數值模擬纖維柔性體運動規律的有效性。

圖6 19.4 tex噴氣渦流紡紗線的表面結構照片(×160)Fig.6 Surface structure of 19.4 tex jet vortex spinning yarn (×160)

圖7 14.5 tex噴氣渦流紡紗線的表面結構(×160)Fig.7 Surface structure of 14.5 tex jet vortex spinning yarn(×160)

4 結 論

基于空間彈性細桿單元建立纖維有限元模型分析了噴氣渦流紡氣流加捻過程中自由端纖維柔性體幾何非線性大變形力學平衡狀態，確立自由端纖維柔性體有限元動力學微分方程，通過MatLab編程數值求解，得到自由端纖維在氣流作用下繞空心錠表面旋轉運動過程中的幾何非線性變形和靜平衡形態，并結合實驗得到了有效驗證。該方法解決了彈性細桿單元有限元分析方法難以用于空間三維幾何非線性大變形實際計算的問題，通過改變數值模擬的初始條件和加載條件，得到不同加捻氣流作用力下的纖維柔性體彈性細桿單元的運動速度和運動軌跡，為噴氣渦流紡成紗過程和原理研究提供了理論基礎和新的研究思路。

FZXB

[1] BECEREN Y, NERGIS B U. Comparison of the effects of cotton yarns produced by new, modified and conventional spinning systems on yarn and knitted fabric performance [J]. Textile Research Journal, 2008, 78(4): 297-303.

[2] BASAL G, OXENHAM W. Effects of some process parameters on the structure and properties of vortex spun yarn [J]. Textile Research Journal, 2006, 76(6): 492-499.

[3] TYAGI G K, SHARMA D, SALHOTRA K R. Process-structure-property relationship of polyester-cotton MVS yarns: part I: influence of processing Variables on Yarn Structural parameters [J]. Indian Journal of Fibre & Textile Research, 2004, 29: 419-428.

[4] 李永霞. 噴氣渦流紡研究[D]. 上海: 東華大學, 2005:4-8.

LI Yongxia. Jet vortex spinning research[D]. Shanghai: Donghua University,2005:4-8.

[5] 李永霞. 噴氣渦流紡初探[J]. 紡織導報, 2005(8): 69-71.

LI Yongxia. Jet vortex spinning exploration[J]. China Textile Leader, 2005(8): 69-71.

[6] 俞兆昇. 噴氣渦流紡紗方法研究[D].上海: 東華大學,2006:10-15.

YU Zhaosheng. Study of jet vortex spinning method[D]. Shanghai: Donghua University,2006:10-15.

[7] ORTLEK H G, NAIR F, KILIK R, et al. Effect of spindle diameter and spindle working period on the properties of 100% viscose MVS yarns [J]. Fibers & Textiles in Eastern Europe, 2008,16(3): 17-20.

[8] LIU Yong, XU Lan. Controlling air vortex in air-vortex spinning by zeng-He mode[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2006, 7(4): 389-392.

[9] GUO Huifen, AN Xianglong, YU Zhaosheng, et al. A numerical and experimental study on the effect of the cone angle of the spindle in murata vortex spinning macgine[J]. ASME Journal of Fluids Engineering, 2008,DOI:10.(1)5/L.2844582.

[10] ZOU Zhuanyong, LIU Shirui, ZHENG Shaoming, et al. Numerical computation of a flow field affected by the process parameters of murata vortex spinning[J]. FIBRES & Textile in Eastern Europe, 2010, 18(2):35-39.

[11] 郭會芬. 噴氣紡紗噴嘴內三維旋轉氣流場及柔性纖維運動的研究[D]. 上海: 東華大學, 2009:10-15.

GUO Huifen. Study on three-dimensional swirling airflow and motion of flexible fiber in air-jet spinning nozzle[D]. Shanghai: Donghua University,2009:10-15.

[12] 劉延柱. 彈性細桿的非線性力學[M]. 北京：清華大學出版社, 2006:10-13.

LIU Yanzhu. Nonlinear Mechanics of Elastic Thin Rods[M]. Beijing: Tsinghua University Press,2006:10-13.

[13] 韓晨晨. 自捻型噴氣渦流紡成紗原理及其紗線結構的相關性研究[D]. 上海: 東華大學, 2016:33-37.

HAN Chenchen. Study on the correlation of yarn formation mechanism and yarn structure in self twist jet vortex spinning[D]. Shanghai: Donghua University, 2016:33-37.

[14] 洪嘉振. 計算多體系統動力學[M]. 北京：高等教育出版社, 1999:13-15.

HONG Jiazhen. Calculation of Multi-System Dynamics[M]. Beijing: Higher Education Press,1999:13-15.